TP 03 unidade 10

TP3 - Unidade 10
TEMA: Semelhança, revestimentos, preenchimentos
O ensino da matemática só tem sentido se contribuir para que o ser humano pense melhor e
viva de forma mais plena.
Ocsana Danyluk
Semelhança
• Em geometria, duas figuras dizem-se semelhantes se uma se pode obter a partir da outra através de isometrias e
homotetias. Como tanto as isometrias como as homotetias preservam os ângulos, duas figuras semelhantes têm a
mesma forma, diferindo apenas pela sua posição e tamanho.
Isometria
• Isometria é uma transformação geométrica que, aplicada a uma figura geométrica, mantém as distâncias entre
pontos. Ou seja, os segmentos da figura transformada são geometricamente iguais aos da figura original, podendo
variar a direção e o sentido. Os ângulos mantêm também a sua amplitude.
• As isometrias simples podem ser rotações, translações e reflexões.
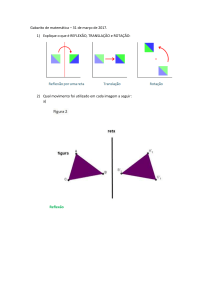
Isometria - Rotações
•
Em álgebra linear e geometria, uma rotação é o tipo de uma transformação de um sistema de coordenadas.
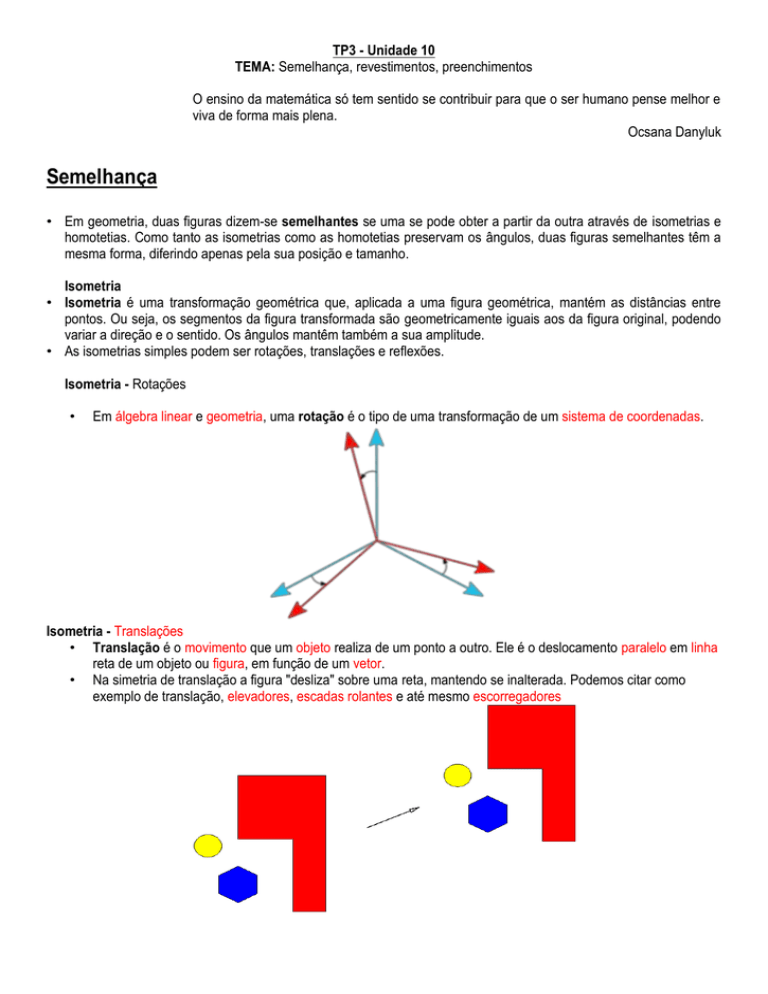
Isometria - Translações
• Translação é o movimento que um objeto realiza de um ponto a outro. Ele é o deslocamento paralelo em linha
reta de um objeto ou figura, em função de um vetor.
• Na simetria de translação a figura "desliza" sobre uma reta, mantendo se inalterada. Podemos citar como
exemplo de translação, elevadores, escadas rolantes e até mesmo escorregadores
Isometria - Reflexões
•
Em Matemática, reflexão é uma transformação geométrica que envolve um ponto a ser refletido e uma reta,
transformando o ponto num outro simétrico com relação ao eixo fornecido.
Homotetias
•
•
Homotetia significa ampliação ou redução das distâncias dos pontos de um espaço em relação a um ponto
fixo. Uma homotetia é definida pelo seu centro O e pela razão k de homotetia e é a aplicação afim tal que a
cada ponto P faz corresponder o ponto P' tal que:
Uma homotetia preserva:
• ângulos
• razões entre segmentos de reta
• segmentos e linhas são transformados em segmentos e linhas paralelos aos originais.
OP  k .OP
Poliedros Regulares
•
•
•
Polígono Regular – Polígono que tem os lados todos iguais e os ângulos geometricamente iguais.
Poliedro – Sólido cujas faces são todas planas.
Poliedro Regular – Poliedro cujas faces são polígonos regulares geometricamente iguais e o número e a
disposição desses polígonos em torno de cada vértice são iguais.
HISTÓRICA AOS SÓLIDOS PLATÔNICOS
A Humanidade, na sua história, estudou a Matemática em ordem inversa à que foi seguida nas suas
escolas, ou quase. De facto a numeração decimal é a primeira coisa que se aprende, mal se vai à
escola, e foi, pelo contrário, uma tardia conquista de uma humanidade já doutíssima em geometria.
Poder-se-ia dizer que a geometria é em vários milhares de anos mais velha do que a Aritmética. Os
gregos tinham um verdadeiro culto pela geometria, que elevaram a um alto grau de perfeição.
Consideravam-na uma ciência que habitua a raciocinar, que refina a inteligência; diziam pelo contrário
que não era preciso estudá-la com fins práticos, mas para "a honra da mente Humana”.
Platão (sec II a.C.9), o grande filósofo aluno de Sócrates, foi o primeiro matemático a demonstrar que
existem apenas cinco poliedros regulares: o cubo, tetraedro, octaedro dodecaedro e o icosaedro. Para
Platão o universo era formado por um corpo e uma alma ou inteligência. Na matéria havia porções
limitadas por triângulos, formando-se elementos que diferem entre si pela natureza da forma das suas
superfícies periféricas. Se forem quadrados temos o cubo- o elemento da terra. Se forem triângulos,
formando um tetraedro, teremos o fogo, cuja natureza penetrante está simbolizada na agudeza dos seus
vértices.
O ar é formado por octaedros e a água de isocaedros. Platão admitia ainda que por intervenção
inteligente, uns se transformavam nos outros à exceção da terra, que se transforma em si própria. O
dodecaedro cheio de harmonia simbolizava o próprio universo. No entanto ainda existem dúvidas se o
teorema" só há cinco sólidos platônicos" se deve a Platão ou a Pitágoras. Mas provar-se-ia mais tarde
que este teorema era falso e Cauchy provou que há nove poliedros regulares e que não existem mais. o
erro do teorema de Platão ou de Pitágoras reside no facto de os poliedros regulares por eles
considerados não serem obrigatoriamente convexos.
Séculos mais tarde Kepler descobriu o primeiro poliedro regular côncavo que é o dodecaedro estrelado
de faces regulares que resulta do prolongamento das faces do dodecaedro. Dois séculos mais tarde
,Louis Poinsot descobriu três novos poliedros regulares não convexos. Na atualidade numerosos
matemáticos, artistas plásticos, designers e arquitetos entusiasmam-se com as propriedades e
aplicações dos poliedros propondo várias formas de os construir e também de os representar em
computador.
LADRILHOS
Um pouco da aula do professor Rogério que de uma maneira criativa trouxe o tema;
Semelhança, revestimentos e preenchimentos.
Pretendo utilizar os ladrilhos nas aulas de geometria plana e creio que conseguirei um trabalho
bonito e com real aprendizagem.