Lista Aprofundamento (UNIFESP 2006) Um numero inteiro positivo

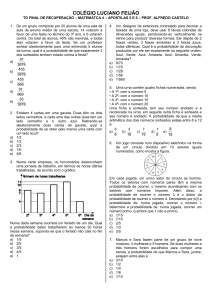
Lista Aprofundamento
1. (UNIFESP 2006) Um numero inteiro positivo m dividido por 15 dá resto 7. A soma dos restos das divisões
de m por 3 e por 5 é: (reposta 3)
2. (UNIFEST 2006) Se 1/(x3+x+1) = 27/37, então 1/(x3+x+2) é igual a: (resposta 64/27)
3. (ITA) O número de diagonais de um polígono regular 2n lados, que não passam pelo centro da
circunferência circunscrita a esse polígono, e dado por: (resposta 2n(n-2))
4. (FGV 2012 1° FASE ECONOMIA) Seja uma função tal que f(xy)= f(x)/y para todos os números reais e
positivos x e y. se f(300) = 5, então o valor de f(700) é igual a. (resposta 15/7)
5.
Obter o conjunto imagem de f:R→R, definida por: f(x) = │2 + 5sen 2x│.
(resposta Im(f) = {y€R/ 0 ≤ y ≤ 7})
6. (MAUÁ –Med 2005) Num triangulo ABC temos AC = 3m, BC = 4m e α = BÂC.
a) Se AB = 3m, calcule cos α. (resposta cos α = 1/9)
̅̅̅̅ for 60°, calcule sen α. ( resposta sen α = 𝟒 , ABSURDO!!!)
b) Se 𝛽 = 𝐴𝐵̂𝐶, oposto ao lado 𝐴𝐶
𝟐√𝟑
7. (FGV 2012 1° FASE ECONOMIA) Considere, no plano cartesiano, o pentágono ABCDE, de vértices
A(0,2), B(4,0), C(2π+1, 0), D(2π+1, 4) e E(0,4).
Escolhendo aleatoriamente um ponto P no interior desse pentágono, a probabilidade de que o ângulo
BPA seja obtuso é igual a: (resposta 5/16)
8.
(FUVEST 1° FASE 2011) Seja x > 0 tal que a sequência a1 = log2x, a2 = log4(4x), a3 = log8(8x) forme nesta
ordem, uma progressão aritmética. Então, a1 + a2 + a3 é igual a: (resposta 15/2)
9. (FUVEST 1° FASE 2011) na figura, tem-se AE paralelo a CD, BC paralelo a DE, AE = 2, α = 45° e β =
75°. Nesses condições, a distância do ponto E ao segmento AB é igual a: (resposta√𝟑)
10. (PUC 1° FASE 2012) Abílio (A) e Gioconda (G) estão sobre uma superfície plana de uma mesma
praia e, num dado instante, veem sob respectivos ângulos de 30º e 45º, um pássaro (P) voando,
conforme é representado na planificação abaixo.
Considerando desprezíveis as medidas das alturas de Abílio e Gioconda e sabendo que, naquele instante, a
distância entre A e G era de 240 m, então a quantos metros de altura o pássaro distava da superfície da
praia: (resposta 120(√𝟑 – 1))
11. (UNESP 1° FASE 2012) Em um programa de plateia da TV brasileira, cinco participantes foram
escolhidos pelo apresentador para tentarem acertar o número de bolas de gude contidas em uma urna
de vidro transparente. Aquele que acertasse ou mais se aproximasse do número real de bolas de gude
contidas na urna ganharia um prêmio. Os participantes A, B, C, D e E disseram haver, respectivamente,
1195, 1184, 1177, 1250 e 1232 bolas na urna. Sabe-se que nenhum dos participantes acertou o número real
de bolas, mas que um deles se enganou em 30 bolas, outro em 25, outro em 7, outro em 48 e, finalmente,
outro em 18 bolas. Podemos concluir que quem ganhou o prêmio foi o participante: (resposta
participante A)
𝑋−𝑌+𝑍 = 2
12. (MACKENZIE 2011) Os valores de k, para que o sistema { 3𝑋 + 𝑘𝑌 + 𝑍 = 1 não tenha solução
−𝑋 + 𝑌 + 𝐾𝑍 = 3
real, são os 2 primeiros termos de uma progressão aritmética de termos crescentes. Então, nessa PA, o
logaritmo na base 3 do quadragésimo terceiro termo é (resposta 4)
13. (UNICAMP 2005 -2 FASE) Sejam A, B, C e N quatro pontos em um mesmo plano, conforme figura
abaixo.
a) Calcule o Raio da circunferência que passa pelos pontos A, B e N? (resposta r = 1)
b) Calcule o comprimento do segmento NB? (resposta NB = √𝟐 )
14. (MACKENZIE 1° FASE 2011) Na figura, os raios das circunferências de centros M e N são,
respectivamente, 2r e 5r. Se a área do quadrilátero AMBN é 16 √6 , o valor de r é : (resposta r = 2)
15. (FUVEST) As paginas de um livro medem 1 dm de base e √1 + √3 dm de altura. Se este livro fica
parcialmente aberto, de tal forma que o ângulo entre duas paginas seja de 60°, a medida do ângulo α,
formado pelas diagonais das paginas, será: (resposta α =30°)
16. /(FUVEST) Calcular o raio X na figura a seguir: (resposta x = 7/10)
17. (FUVEST 1°FASE 2002) Numa barraca de feira, uma pessoa comprou maçãs, bananas, laranjas e peras.
Pelo preço normal da barraca, o valor pago pelas maçãs, bananas, laranjas e peras corresponderia a 25%,
10%, 15% e 50% do preço total, respectivamente. Em virtude de uma promoção, essa pessoa ganhou um
desconto de 10% no preço das maçãs e de 20% no preço das peras. O desconto assim obtido no valor total
de sua compra foi de: (resposta 12,5%).
18. (FUVEST 1° FASE 2002) Na figura ao lado, o quadrilátero ABCD está inscrito numa semicircunferência
de centro A e raio AB = AC = AD =R. A diagonal AC forma com os lados BC e AD ângulos α e β e
respectivamente. Logo, a área do A quadrilátero ABCD é: (resposta A = (R2/2).(sen2α + cosβ)
19. (UFABC 2008) O segmento AB é simultaneamente diâmetro de um circulo de raio 2 e lado do triângulo
equilátero ABC. O circulo intersecta os segmentos AC e BC nos pontos D e E, respectivamente. Faça uma
figura representando a situação descrita e calcule o comprimento do segmento AE. (resposta: desenho e
AE = 2√𝟑 )
20. (ITA 2005) em um triangulo retângulo, a medida da mediana relativa a hipotenusa é a média
geométrica das medidas dos catetos. Então, o valor do cosseno de um dos ângulos do triangulo é
𝟏
igual a: (resposta . √𝟐 − √𝟑)
𝟐
21. (ITA 2004) Considerando as funções arcsen e arccos, assinale o valor de:
cos [arcsen(3/5) + arccos(4/5)]. (resposta 7/25)
22. (Acad. Barro Branco 2010) A figura mostra, no plano complexo, o círculo de centro na origem e
raio 1 e mais cinco números complexos X, Y, Z, W, R. Um desses cinco números é igual a 1/z.
O numero complexo 1/z é igual a qual ponto denotado na figura? (resposta Y).