Aula 20

MATEMÁTICA
1° ANO
ENSINO MÉDIO
PROF. ALEXANDRE DOS SANTOS
PROF. EMERSON MARÃO
CONTEÚDOS E HABILIDADES
Unidade IV
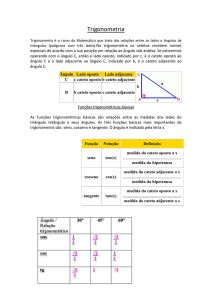
Trigonometria
2
CONTEÚDOS E HABILIDADES
Aula 20.1
Conteúdo
Seno, cosseno e tangente
3
CONTEÚDOS E HABILIDADES
Habilidade
Utilizar as relações, seno cosseno e tangente na resolução
de problemas.
4
REVISÃO
Teorema de Pitágoras
Em todo triângulo retângulo o quadrado da medida da
hipotenusa é igual à soma dos quadrados das medidas dos
catetos.
a =b
2
2
+c
2
5
REVISÃO
Tendo a medida de dois lados de um triângulo retângulo,
podemos usar o Teorema de Pitágoras para descobrir o
valor do terceiro lado. Por exemplo:
x = 12 + 9
2
x
2
2
x = 144+81
2
9
x = 225
2
√x = √225
2
12
x=15
6
DESAFIO DO DIA
Qual nome do instrumento que a moça está usando?
Sabem dizer onde é usado e para que serve?
7
AULA
Razões Trigonométricas.
Seno: razão entre o cateto oposto a um ângulo de um
triângulo retângulo e a hipotenusa
Hipotenusa
60o
Cateto
cateto oposto a 30º
Sen 30º =
hipotenusa
CO
=
H
cateto oposto a 60º
Sen 60º =
hipotenusa
CO
=
H
oposto
a 30o
30o
Cateto oposto a 60o
CO
Sen α = H
8
AULA
Exemplo prático:
(Unisinos – RS) Um avião levanta voo sob um ângulo
constante de 20º. Após percorrer 2 000 metros em
linha reta, qual será a altura atingida pelo avião,
aproximadamente?
(Utilize: sen 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364)
2000 metros
h=?
20
o
9
AULA
Resolução: Como devemos utilizar o cateto oposto ao
ângulo de referência e temos conhecimento da hipotenusa,
a razão trigonometria seno
cateto oposto
h
→ 0,342 =
Seno 20º =
→ h=684
hipotenusa
2000
Resposta: 684 metros
10
AULA
Cosseno: razão entre o cateto adjacente a um ângulo de um
triângulo retângulo e a hipotenusa.
Hipotenusa
60o
Cateto Adjacente a 30º
Cos 30º =
Hipotenusa
Cateto
oposto
a 30o
30o
Cateto oposto a 60o
Cateto Adjacente a 60º
Cos 60º =
Hipotenusa
CA
Cos α = H
11
AULA
Exemplo:
Uma escada de 8 m foi encostada na parede da sala de aula
o
formando com o chão um ângulo de 60 . Com estes dados,
determine, sem ter mais nenhuma medida, a que distância
está a base da escada da parede.
Dados: cosseno de 60 = ½
o
8m (escada)
x
60
o
12
AULA
Resolução: Pelas informações do problema e fazendo uma
análise do desenho, deveremos usar a relação cosseno, ou
seja:
x
1
x
8
0
cos60 = → = → 2x = 8 → x = = 4
8
2 8
2
Resposta: 4 metros
8m (escada)
x
60
o
13
DINÂMICA LOCAL INTERATIVA
1. Um avião levanta voo sob um ângulo de 30°. Após
percorrer 16 km em linha reta, qual a sua altura em
relação ao solo?
(sen 30°= ½).
16 km
30
x
o
14
DINÂMICA LOCAL INTERATIVA
2. Sabendo que sen 28° = 0,46; cos 28º = 0,88 e tg 28° =
0,53, calcule o valor de x nos exemplos a seguir:
15