PrimeiraLeidaTermodinâmica
Prof.MarcoSimões
CaloreTrabalho
• Atermodinâmica
estudaarelação
entrecaloretrabalho
• Conforme
determinadopor
Joule
• 1cal=4,18J
• esseéoequivalente
mecânicodocalor.
• Aenergiamecânicae
atérmicasão
equivalentes
MáquinadeHeron,séc.IdC.
Exemplo
• Qualaelevaçãodatemperaturadeumamassade
águade10kgquecaideumaalturade850m?
Exemplo
• Paratransformarumsundaecomcaldaquentede
900caloriasalimentaresemenergia,vocêpretende
subircorrendovárioslancesdeescada.Sabendoque
1caloriaalimentaréiguala1kcal,qualaalturaque
vocêdevesubirpara‘queimaressascalorias’e
manterseus60kg?
Resolução
Trabalhorealizadoporumgás
• Quantoumgásseexpandeele
realizatrabalhosobreomeio
– Otrabalhoéposi*vo
• Quantoumgásécomprimido,
omeiorealizaumtrabalho
sobreele
– Otrabalhoénega*vo
• Quantonãohávariaçãode
volume,nãohátrabalho
– Otrabalhoéigualazero
→
W > 0
←
W < 0
Energiainternadeumgásideal
• Amatériaécons[tuídademoléculaseestassão
par]culasquepossuemenergiaciné[caeenergia
potencial
• Aenergiainternaésimplesmenteéasomadas
energiasciné[caepotencialdetodassuas
par]culas,eédadapor:
PrimeiraLeidaTermodinâmica
• QuandofornecemoscalorQaumgáseelenãorealiza
nenhumtrabalho(i.e.seuvolumenãovaria)duranteo
processo,aenergiainternaaumentadeumvalorigualaQ;
ΔU
=
Q
• Quandoumgásseexpande(istoé,realizatrabalho,W)e
nenhumcaloréfornecidoaosistemanesteprocesso,sua
energiainternadiminui,ouseja,quandoWéposi[voΔUé
nega[vo,evice-versa.
ΔU = −W
PrimeiraLeidaTermodinâmica
• Quandoosdoiseventosacontecem
simultaneamente,istoé,ogásrecebecalorese
expande,avariaçãodasuaenergiainternaserá:
ΔU
=
Q
−W
• EssarelaçãoéaPrimeiraLeidaTermodinâmica:
– Avariaçãodaenergiainternadeumgásidealédadapela
diferençaentreaquan[dadedecalortrocadacomomeio
eotrabalhorealizadonoprocesso
Exemplos
• Determineavariaçãodaenergiainternanosseguintescasos
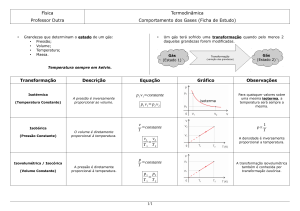
Tiposdetransformação
• Há4processosnosquaisosgasespodemtrocar
calore/outrabalhocomomeio.
A-Isocórica
D-Isobárica
C-Isotérmica
B-Adiabá[ca
Transformaçãoisobárica
• Nessatransformação,apressãopermanece
constante
• Otrabalhorealizadopelopistãoserá:
W = F ⋅d
Transformaçãoisobárica
Massabemosque:
F
p = ⇒ F = p⋅ A
A
Juntandoasduas,temos:
W = F ⋅d
W = p⋅ A⋅d
ComoA⋅d = ΔV ,temosque:
W
=
p⋅ΔV
Transformaçãoisobárica
• Comoháfornecimento/produçãodetrabalhoe
tambémháfornecimento/produçãodecalor,paraa
transformaçãoisobáricaseráverdadeque:
ΔU = QP −W
Transformaçãoisobárica
• Sefizermosarepresentaçãográficadoanterior,
teremos,veremosqueotrabalhoéaárea
sombreada.Issoseráverdademesmoqueapressão
nãoforconstante
Transformaçãoisobárica
• Calortrocado
QP = m⋅cP ⋅ΔT
• Ou
QP = n⋅C P ⋅ΔT
Q P ⇒ calortrocadoapressão
constante,calouJ
m ⇒ massa,kg
c P ⇒ calorespecíficoapressão
constante,cal/kg.KouJ/kg.K
ΔT ⇒ variaçãodetemperatura,˚CouK
CP ⇒ calorespecíficomolar
apressãoconstante,
cal/mol.KouJ/mol.K
Caloresespekciosdegases
Exemplo
• 5,0molesdeumgásperfeitosofremuma
transformaçãoisobáricadescritanográficoabaixo.
Determine:
• apressãodogás
• otrabalhorealizadono
processo
• avariaçãodaenergia
internadogás
• aquan[dadedecalor
queogástrocacomo
ambiente
• ocalormolardogása
temperaturaconstante
Resolução
Resolução
Transformaçãoisocórica
• Natransformaçãoisocóricanãohávariaçãode
volume.Portantonãohárealizaçãodetrabalho.
W = 0
• Ocalortrocadoserádadoporumadasregras:
QV = m⋅cV ⋅ΔT QV = n⋅CV ⋅ΔT
• Comonãohátrabalho,avariaçãodaenergiainterna
será:
ΔU = QV −W ⇒ ΔU = QV − 0 ⇒ ΔU = QV
RelaçãodeMayer
• Consideremosduasamostrasiguaisdegásqueterão
suastemperaturasaumentadasdeT1paraT2por
mosmodosdiferentes:
AB–Isobárico
AC–Isocórico
RelaçãodeMayer
NoprocessoABtemosque:
ΔU = QP -W
NoprocessoAC,temosque:
ΔU = QV
Igualando:
QP -W = QV ⇒ W = QP − QV
Jávimosque:
PV = nRT ∴PΔV = nRΔT
W = P ⋅ΔV ∴W = nRΔT
QP = n⋅C P ⋅ΔT
Q = n⋅CV ⋅ΔT
V
Portanto:
W = QP − QV
n⋅R⋅ΔT = n⋅C P ⋅ΔT − n⋅CV ⋅ΔT
R = C P − CV
RelaçãodeMayer
• Épossíveltambémestabelecerumarelaçãoentreos
caloresespecíficos
W = QP − QV
n⋅R⋅ΔT = m⋅cP ⋅ΔT − m⋅cV ⋅ΔT
m
ComoM = ⇒ m = n⋅M
n
Substituindo,vem:
n⋅R⋅ΔT = n⋅M ⋅cP ⋅ΔT − n⋅M ⋅cV ⋅ΔT
R = M ⋅cP − M ⋅cV
(
R = M ⋅ cP − cV
)
Exemplo
• Atemperaturade4,0molsdeumgásidealeleva-se
de100Kpara600Knumaquecimentoisobárico
(AB).Sendo20,8J/mol.Kocalormolardogása
pressãoconstanteeR=8,3J/mol.Kaconstante
universaldosgasesperfeitos,determine:
a)aquan[dadedecalorrecebidapelogás
nesseprocessoAB(isobárico)
b)aquan[dadedecalorqueogás
receberiasesofresseomesmo
aquecimentoavolumeconstante
(isocórico)–curvaAC
c)otrabalhorealizadopelogásno
processoisobárico
Resolução
Resolução
Transformaçãoisotérmica
• Comonãohávariaçãodetemperatura,nãohá
variaçãodaenergiainterna.
• Assim:
ΔU = Q −W
0 = Q −W
W
=
Q
Exemplo
• Certamassadegásperfeitotrocacomomeio
ambiente100calorias,naformadecalor.Sendo1
cal=4,19J,determine:
a)otrabalhotrocadoentreogáseomeio,expressoem
Joules,sesuatransformaçãoéumaexpansãoisotérmica
b)otrabalhotrocadoentreogáseomeio,expressoem
Joules,sesuatransformaçãoéumacompressãoisotérmica
c)avariaçãodaenergiainternanascondiçõesanteriores
Resolução
Transformaçãoadiabá[ca
• Sãoprocessosemqueogássofreumacompressãoe
expansãotãorápidas,queatrocadecalorcomo
meioédesprezivel
ΔU = Q −W
ΔU = 0−W
ΔU = −W
Nessatransformação,avariaçãoda
energiainternadogásserá
numericamenteigualaotrabalho
aplicadosobreele.
Transformaçãoadiabá[ca
• Naexpansãoadiabá[caatemperaturadiminui,ovolumeaumentaea
pressãodiminui.
• Nacompressãoadiabá[caatemperaturaaumenta,ovolumediminuiea
pressãoaumenta
• Érepresentadoporumahipérbolenãoequilátera
Transformaçãoadiabá[ca
• Numatransformaçãoadiabá[ca,osgasesseguema
leigeraldosgases:
P1V1
T1
=
P2V2
T2
• EtambémaleidePoisson:
γ
1
γ
2
P1 ⋅V = P2 ⋅V
γ −1
1
T1 ⋅V
γ −1
2
= T2 ⋅V
γ = coeficientede
Poisson
cP C P
γ= =
cV CV
Exemplo
• Emumatransformaçãoadiabá[caumgásexecuta
umtrabalhode800J.Pergunta-se
a.
b.
c.
d.
Ocorreuexpansãooucontraçãodogás?
Qualaquan[dadedecalortrocadacomomeio?
Qualavariaçãodaenergiainternadogás?
OqueaconteceucomasvariáveisP,VeT?
Resolução
a)Ocorreuexpansãooucontraçãodogás?
Otrabalhofoirealizadopelogás.Portantohouveexpansão.
b)Qualaquan[dadedecalortrocadacomomeio?
Natransformaçãoadiabá[canãohátrocadecalorcomomeio.
c)Qualavariaçãodaenergiainternadogás?
ΔU = Q −W ⇒ ΔU = 0− 800 ⇒ ΔU = −800 J
Portantoaenergiainternadogásdiminuiuem800J
Resolução
d)OqueaconteceucomasvariáveisP,VeT?
Comootrabalhoéposi[vo,oVaumentou.
Comoaenergiainternadiminuiu,Tdiminui.
Pelaequaçãodosgasesperfeitos
PV
PV
PV = nRT ⇒
= nR,ouseja
= constante
T
T
Portanto,Pdeveteraumentado,poisnafração:
V↑
V
,istoé, ↑ .Paramanteraconstante,Pdeveter
T↓
T
diminuído.
V
P ↓ ⋅ ↑= constante
T
Exemplo
• Umgásperfeitoocupaovolumede8litrossob
pressãode2atm.Apósumatransformação
adiabá[ca,ovolumedogáspassoua2litros.Sendo
oexpoentedePoissonγ=1,5,determineanova
pressãodogás.
P1V1γ = P2V2γ
P2 =
P1V1γ
V2γ
1,5
2⋅8
P2 = 1,5 ⇒ P2 = 16 atm
2
Resumodastransformações
Processoscíclicosdeumgás
• Sãoaquelesemqueogás,depoisderealizá-los,ogásretorna
aoseuestadoinicialdepressão,volumeetemperatura
• Comoatemperaturafinaléigualàinicial,nãohávariaçãoda
energiainterna
ΔU = Q −W
0 = Q −W
Q
=
W
Processoscíclicosdeumgás
• LembrandoqueotrabalhocorrespondeàáreadográficoPx
V,épossívelconcluirquequandoocicloforhorário,o
trabalhoseráposi[vo:
A
W
B
W
=
A
−
B
⇒
A
>
B∴W
>
0
Processoscíclicosdeumgás
• Quandoocicloforan[-horário,otrabalhoserá
nega[vo:
W<0
A
B
W
=
A
−
B
⇒
A
<
B∴W
<
0
Exemplosdeprocessoscíclicos
Exemplo
• OdiagramaPxVabaixomostraumciclorealizado
porumacertamassadeumgásperfeito
Calcule:
a) avariaçãodaenergia
internadogás
b) otrabalhorealizadono
ciclo
c) aquan[dadedecalor
trocadacomomeio
d) nessecicloocaloré
transformadoem
trabalhoouvice-versa?
Resolução
Resolução