1ª Lei da Termodinâmica – Intermediário 2

PRIMEIRA LEI DA TERMODINÂMICA – INTERMEDIÁRIO 2
Exercícios resolvidos
1. (IME 2007) Uma massa m de ar, inicialmente a uma pressão de 3 atm, ocupa 0,1 m3 em um balão. Este gás é expandido
isobaricamente até um volume de 0,2 m3 e, em seguida, ocorre uma nova expansão através de um processo isotérmico, sendo
o trabalho realizado pelo gás durante esta última expansão igual a 66000 J. Determine:
a) o trabalho total realizado em joules pelo gás durante todo o processo de expansão;
b) o calor total associado às duas expansões, interpretando fisicamente o sinal desta grandeza.
Cp
kgf
= 1,4.
Dados: 1 atm = 1 2 ,1 kgf = 10 N e γ =
C
cm
v
Obs.: suponha que o ar nestas condições possa ser considerado como gás ideal.
Solução
a) O trabalho total do gás durante o processo de expansão é a soma dos trabalhos em cada etapa. Só existem duas etapas:
expansão isobárica e expansão isotérmica.
Wtotal = Wisobárica + Wisotérmica
O trabalho realizado na transformação isobárica é calculado por Wisobárica = pΔV . Convertendo a pressão de atm para Pa
(unidade no SI), temos 1atm ≡ 10 Pa . Daí:
5
Wisobárica = 3.105. ( 0, 2 − 0,1) ⇒ Wisobárica = 3.104 J
Wtotal = 3.104 + 66000 = 9, 6.104 J
b) O enunciado informa
γ=
ΔU = nCV ΔT . Logo, ΔU =
Cp
Cv
=1, 4 . Como C p − CV = R , podemos encontrar CV =
5
5
nRΔT = Δ( pV ) .
2
2
5
5
Δ ( pV ) = × 3.105 × ( 0, 2 − 0,1) ⇒ ΔU = 7,5.104 J .
2
2
A etapa isotérmica tem ΔU = 0 .
4
Logo, ΔU total = 7,5.10 J .
A etapa isobárica tem
ΔU =
Da 1ª. Lei da Termodinâmica, vem:
ΔU = Q − W ⇒ 7,5.104 = Q − 9, 6.104
⇒ Q = 17,1.104 J
Com Q > 0, o gás recebeu energia térmica ao longo do processo de expansão.
5
R . Sabemos que
2
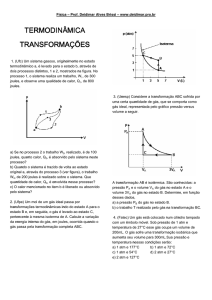
2. (AFA 2007) A variação volumétrica de um gás, em função da temperatura, à pressão constante de 6 N/m2 está indicada no
gráfico.
Se, durante a transformação de A para B, o gás receber uma quantidade de calor igual a 20 joules, a variação da energia
interna do gás será igual, em joules, a:
(A) 32
(B) 24
(C) 12
(D) 8
Solução
Pela 1ª. Lei da Termodinâmica: ΔU = Q − W . A quantidade de calor associada a este processo é informada no enunciado:
20 J. Logo, precisamos calcular o trabalho.
Como o processo é isobárico, Wisobárica = pΔV . Daí:
Wisobárica = 6. ( 4 − 2 ) ∴W = 12 J
ΔU = Q − W
⇒ ΔU = 20 − 12 J ∴ΔU = 8 J
Opção D
Exercícios propostos
1. (ITA 2004) Um recipiente cilíndrico vertical é fechado por meio de um pistão, com 8,00 kg de massa e 60,0 cm2 de área,
que se move sem atrito. Um gás ideal, contido no cilindro, é aquecido de 30 ºC a 100 ºC, fazendo o pistão subir 20,0 cm.
Nesta posição, o pistão é fixado, enquanto o gás é resfriado até sua temperatura inicial. Considere que o pistão e o cilindro
encontram-se expostos à pressão atmosférica. Sendo Q1 o calor adicionado ao gás durante o processo de aquecimento e Q2, o
calor retirado durante o resfriamento, assinale a opção correta que indica a diferença Q1 – Q2.
(A) 136 J
(B) 120 J
(C) 100 J
(D) 16 J
(E) 0 J.
2. (AFA 1998) No diagrama pressão-volume, indicado na figura, um sistema sofre uma transformação do estado inicial i para
o estado final f. Caso tal fenômeno ocorra, tendo como estado intermediário o ponto A, o calor absorvido e o trabalho
realizado, em joules, serão, respectivamente, 50 e 20. Entretanto, se for utilizado como estado intermediário o ponto B, o calor
absorvido será 36 J. A energia interna inicial tem valor 10 J.
P
A
f
i
B
V
Então, a energia interna final e o trabalho realizado segundo a trajetória i B f, valem, respectivamente, em joules,
(A) 10 e 6
(B) 20 e 36
(C) 30 e 20
(D) 40 e 6
3. (ITA 1994) Aquecendo-se lentamente 2 moles de um gás perfeito ele passa do estado P , V ao estado 3P , 3V . Se o
0
0
0
0
gráfico da pressão versus volume é uma reta, a dependência da temperatura com o volume e o trabalho realizado pelo gás
nesse processo serão respectivamente:
2
(A) T=( P V ) / ( V R); W = 9,0 P V
0
2
0
0
0
(B) T=( P V ) / ( 2V R); W = 4,0 P V
0
0
2
0
(C) T=( P V ) / ( 2V R); W = 2,0 P V
0
0
(D) T=( P V ) / (R); W = 2,0 P V
0
0
2
0
0
0
0
0
(E) T=( P V ) / ( V R); W = 4,5 P V
0
0
0
0
4. (ITA 1992) Uma molécula-grama de gás ideal sofre uma série de transformações e passa sucessivamente pelos estados
A→B→C→D, conforme o diagrama PxV ao lado, onde T = 300K. Pode-se afirmar que a temperatura em cada estado, o
A
trabalho líquido realizado no ciclo e a variação da energia interna no ciclo são respectivamente:
(A)
(B)
(C)
(D)
(E)
Gabarito
1. A
2. D
3. B
4. A
TA (K)
300
300
300
300
300
TB (K)
900
900
450
900
450
TC (K)
450
450
900
450
900
TD (K)
150
150
150
150
300
W (atm.L)
20,0
-20,0
20,0
60,0
80,0
ΔU(J)
0
0
0
40
60