1. (Mack-2005) Um trenzinho, de 60cm de comprimento, descreve

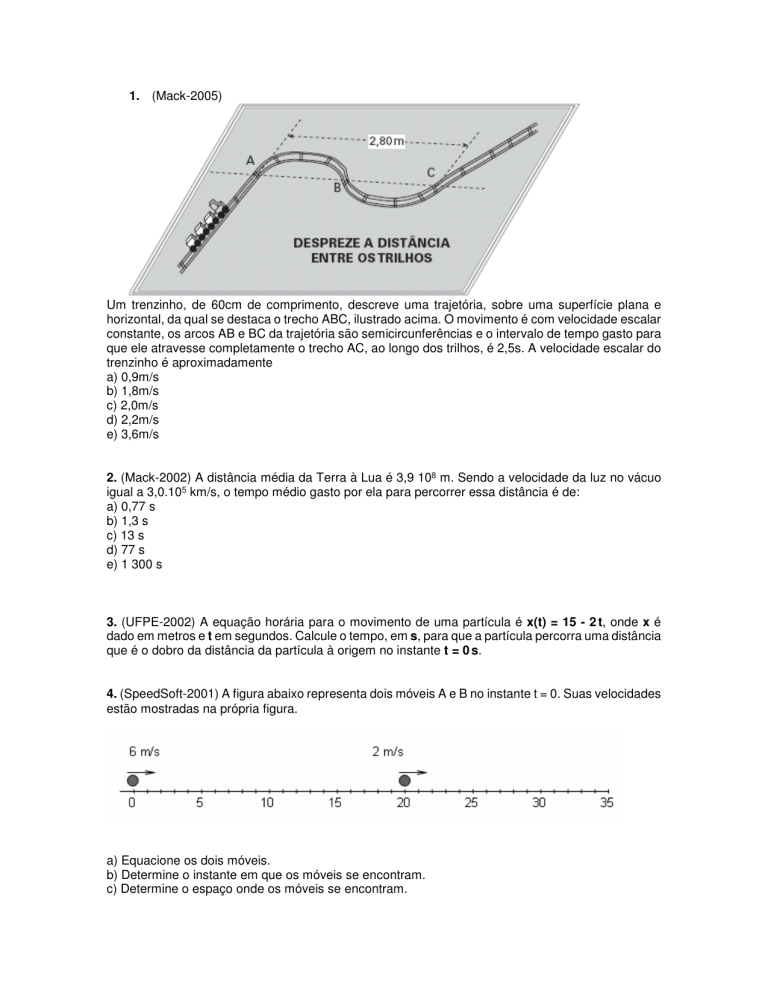
1. (Mack-2005)
Um trenzinho, de 60cm de comprimento, descreve uma trajetória, sobre uma superfície plana e
horizontal, da qual se destaca o trecho ABC, ilustrado acima. O movimento é com velocidade escalar
constante, os arcos AB e BC da trajetória são semicircunferências e o intervalo de tempo gasto para
que ele atravesse completamente o trecho AC, ao longo dos trilhos, é 2,5s. A velocidade escalar do
trenzinho é aproximadamente
a) 0,9m/s
b) 1,8m/s
c) 2,0m/s
d) 2,2m/s
e) 3,6m/s
2. (Mack-2002) A distância média da Terra à Lua é 3,9 108 m. Sendo a velocidade da luz no vácuo
igual a 3,0.105 km/s, o tempo médio gasto por ela para percorrer essa distância é de:
a) 0,77 s
b) 1,3 s
c) 13 s
d) 77 s
e) 1 300 s
3. (UFPE-2002) A equação horária para o movimento de uma partícula é x(t) = 15 - 2 t, onde x é
dado em metros e t em segundos. Calcule o tempo, em s, para que a partícula percorra uma distância
que é o dobro da distância da partícula à origem no instante t = 0 s.
4. (SpeedSoft-2001) A figura abaixo representa dois móveis A e B no instante t = 0. Suas velocidades
estão mostradas na própria figura.
a) Equacione os dois móveis.
b) Determine o instante em que os móveis se encontram.
c) Determine o espaço onde os móveis se encontram.
5. (Unicamp-1999) A figura mostra o esquema simplificado de um dispositivo colocado em uma rua
para controle de velocidade de automóveis (dispositivo popularmente chamado de radar).
Os sensores S1 e S2 e a câmera estão ligados a um computador. Os sensores enviam um sinal ao
computador sempre que são pressionados pelas rodas de um veículo. Se a velocidade do veículo
está acima da permitida, o computador envia um sinal para que a câmera fotografe sua placa traseira
no momento em que esta estiver sobre a linha tracejada. Para um certo veículo, os sinais dos
sensores foram os seguintes:
a) Determine a velocidade do veículo em km/h.
b) Calcule a distância entre os eixos do veículo.
6. (Fatec-1995) A tabela fornece, em vários instantes, a posição s de um automóvel em relação ao
km zero da estrada em que se movimenta.
t (h)
S (km)
0,0
200
2,0
170
4,0
140
6,0
110
8,0
80
10,0
50
A função horária que nos fornece a posição do automóvel, com as unidades fornecidas, é:
a) s = 200 + 30t
b) s = 200 - 30t
c) s = 200 + 15t
d) s = 200 - 15t
e) s = 200 - 15t
7. (Unicamp-2003) A velocidade linear de leitura de um CD é 1,2m/s.
a) Um CD de música toca durante 70 minutos, qual é o comprimento da trilha gravada?
b) Um CD também pode ser usado para gravar dados. Nesse caso, as marcações que representam
um caracter (letra, número ou espaço em branco) têm 8µm de comprimento. Se essa prova de Física
fosse gravada em um CD, quanto tempo seria necessário para ler o item a) desta questão? 1µm =
10-6m.
8. (UERJ-1997) A velocidade normal com que uma fita de vídeo passa pela cabeça de um gravador
é de, aproximadamente, 33 mm/s. Assim, o comprimento de uma fita de 120 minutos de duração
corresponde a cerca de:
a) 40 m
b) 80 m
c) 120 m
d) 240 m
e) 360 m
9. (SpeedSoft-2001) Dois móveis A e B se deslocam na trajetória indicada abaixo, com velocidades
de módulos VA = 15 m/s e VB = 10 m/s.
a) Equacione os dois móveis.
b) Determine o instante de encontro.
c) Determine a posição de encontro.
d) Num mesmo diagrama S x t, construa os gráficos dos dois móveis, indicando o instante e a posição
de encontro.
10. (FEI-1997) Dois móveis A e B, ambos com movimento uniforme percorrem uma trajetória retilínea
conforme mostra a figura. Em t = 0, estes se encontram, respectivamente, nos pontos A e B na
trajetória. As velocidades dos móveis são vA = 50 m/s e vB = 30 m/s no mesmo sentido.
Em qual ponto da trajetória ocorrerá o encontro dos móveis?
a) 200 m
b) 225 m
c) 250 m
d) 300 m
e) 350 m
11. (VUNESP-2006) Duas carretas, A e B, cada uma com 25m de comprimento, transitam em uma
rodovia, no mesmo sentido e com velocidades constantes. Estando a carreta A atrás de B, porém
movendo-se com velocidade maior que a de B, A inicia uma ultrapassagem sobre B. O gráfico mostra
o deslocamento de ambas as carretas em função do tempo. Considere que a ultrapassagem começa
em t = 0, quando a frente da carreta A esteja alinhada com a traseira de B, e termina quando a
traseira da carreta A esteja alinhada com a frente de B. O instante em que A completa a
ultrapassagem sobre B é
a) 2,0s.
b) 4,0s.
c) 6,0s.
d) 8,0 s.
e) 10,0s.
12. (UERJ-1998) A cidade de São Paulo tem cerca de 23 km de raio. Numa certa madrugada, partese de carro, inicialmente em repouso, de um ponto qualquer de uma das avenidas marginais que
circundam a cidade. Durante os primeiros 20 segundos, o movimento ocorre com aceleração
constante de 1,0 m/s2. Ao final desse período, a aceleração torna-se nula e o movimento prossegue
mantendo-se a velocidade adquirida.
Considerando que o movimento foi circular, determine:
a) a distância percorrida pelo carro durante os primeiros 20 segundos;
b) o tempo gasto para alcançar-se o ponto diametralmente oposto à posição inicial, ou seja, o
extremo oposto da cidade.
13. (SpeedSoft-2001) A equação horária de um móvel é :
S = 5 - 2t + t2 (SI)
a) calcule seu espaço inicial, sua velocidade inicial e sua aceleração
b) escreva a equação horária da velocidade
c) calcule sua velocidade no instante t = 5s.
14. (SpeedSoft-2002) A equação horária que fornece a velocidade de uma pedra lançada
verticalmente para cima é:
V = 30 - 10.t
(SI)
Determine:
a) a velocidade inicial e a aceleração da pedra
b) a velocidade da pedra no instante t = 4 s
c) verifique se há inversão no sentido de movimento,e se houver, em que instante isso ocorre.
d) classifique o movimento nos instantes t = 2 s e t = 4 s.
e) construa o gráfico V x t (de 0 até 6 s).
15. (UNIFESP-2008) A função da velocidade em relação ao tempo de um ponto material em trajetória
retilínea, no SI, é v = 5,0 – 2,0t. Por meio dela pode-se afirmar que, no instante t = 4,0 s, a velocidade
desse ponto material tem módulo
a) 13 m/s e o mesmo sentido da velocidade inicial.
b) 3,0 m/s e o mesmo sentido da velocidade inicial.
c) zero, pois o ponto material já parou e não se movimenta mais.
d) 3,0 m/s e sentido oposto ao da velocidade inicial.
e) 13 m/s e sentido oposto ao da velocidade inicial.
16. (UEL-1995) A função horária da posição de um móvel que se desloca sobre o eixo dos x é, no
Sistema Internacional de Unidades, x = -10 + 4t + t2. A função horária da velocidade para o referido
movimento é:
a) v = 4 + 2t
b) v = 4 + t
c) v = 4 + 0,5t
d) v = -10 + 4t
e) v = -10 + 2t
17. (PUC-Camp-1995) A função horária da posição s de um móvel é dada por s = 20 + 4t - 3t2, com
unidades do Sistema Internacional. Nesse mesmo sistema, a função horária da velocidade do móvel
é:
a) V = -16 - 3t
b) V = -6t
c) V = 4 - 6t
d) V = 4 - 3t
e) V = 4 - 1,5t
18. (UDESC-1998) A tabela fornece, em vários instantes, as velocidades de um móvel que, partindo
da origem (x = 0 no instante t = 0), desloca-se em trajetória retilínea e em movimento uniformemente
acelerado.
A partir dessas informações podemos afirmar que, no S.I., a função velocidade, v = f(t), e a função
horária, x = f(t), desse movimento são, respectivamente:
a) v = 3t e x = 1,5t2
b) v = 3 + 3t e x = 3t + 3t2
c) v = 1,5t e x = 3t + 1,5t2
d) v = 3t e x = 3t + 1,5t2
e) v = 3t e x = 3t2
19. (UEL-1996) A velocidade de um objeto, em movimento retilíneo, varia com o tempo de acordo
com o gráfico a seguir.
Pode-se afirmar corretamente que:
a) no intervalo de tempo de 2 s a 6 s, o deslocamento do objeto tem módulo 80m.
b) o movimento é acelerado desde t = 0 a t = 6s.
c) a aceleração do movimento tem módulo 7,5m/s2.
d) a aceleração é nula no instante t = 2s.
e) nos instantes t = 0 e t = 4s, o móvel se encontra na mesma posição.
20. (PUC-SP-2001) Ao iniciar a travessia de um túnel retilíneo de 200 metros de comprimento, um
automóvel de dimensões desprezíveis movimenta-se com velocidade de 25m/s. Durante a travessia,
desacelera uniformemente, saindo do túnel com velocidade de 5m/s.
O módulo de sua aceleração escalar, nesse percurso, foi de:
a) 0,5m/s2
b) 1,0m/s2
c) 1,5m/s2
d) 2,0m/s2
e) 2,5m/s2
21. (UFSCar-2004) Considere as quatro afirmações seguintes.
I.
No MRUV, a velocidade varia linearmente com o tempo.
II.
Um carro em marcha à ré não pode realizar movimento acelerado.
III.
O coeficiente angular da reta que você obtém ao construir o gráfico da velocidade x tempo
fornece a velocidade inicial do móvel.
IV.
Pode-se determinar a velocidade de um móvel no MRUV, sem conhecer o tempo de percurso
do móvel.
Das afirmações apresentadas, são verdadeiras:
a) I e II, apenas.
b) I e III, apenas.
c) I e IV, apenas.
d) II e IV, apenas.
e) III e IV, apenas.
22. (UFMS-2003) Considere o gráfico do espaço em função do tempo para uma partícula em
movimento uniformemente variado. É correto afirmar que:
a) a trajetória da partícula foi parabólica.
b) a partícula não passou pela origem dos espaços.
c) a velocidade da partícula jamais foi nula.
d) a velocidade inicial da partícula foi negativa.
e) a aceleração da partícula foi inicialmente positiva, depois negativa.
23. (UECE-2006) Dois carros viajando na mesma direção e mesmo sentido se encontram no início
da subida de uma ladeira de inclinação constante e igual a 30º. Nesse instante, o carro I tem
velocidade de 20 m/s e o II,
5 m/s. Neste ponto, o carro I desliga o motor, enquanto o II continua
com a mesma velocidade. Despreze todas as forças de atrito e considere g = 10 m/s2. Após quantos
metros os carros se encontrarão novamente?
a) 5
b) 15
c) 20
d) 30
24. (Mack-2008) Duas cidades, A e B, são interligadas por uma estrada com 50km de comprimento.
Em certo instante, um automóvel parte do repouso, da cidade A rumo à cidade B, com aceleração
escalar constante de 1,0m/s2, durante 20s. Após esse tempo, sua velocidade escalar permanece
constante. No instante em que esse automóvel parte da cidade A, um outro automóvel passa pela
cidade B, dirigindo-se à cidade A, com velocidade escalar constante de 108km/h. A distância, relativa
à cidade A, medida ao longo da estrada, em que ocorre o encontro desse dois automóveis, é
a) 20,12km
b) 19,88km
c) 19,64km
d) 19,40km
e) 19,16km
25. (FEI-0) A figura abaixo mostra a variação da velocidade v de um corpo em função do tempo.
Calcule:
a) a aceleração do corpo
b) a distância percorrida pelo móvel entre 0 e 10 segundos.
26. (UFPE-2002) A figura mostra a variação da velocidade escalar de dois pequenos blocos que se
movem em sentidos opostos, na direção vertical. No instante em que o bloco A cai do alto de um
edifício de 94 m de altura, o bloco B é lançado a partir do solo, ao longo da mesma linha vertical.
Qual é a distância entre os blocos, em m, no instante em que as suas velocidades escalares têm o
mesmo valor? Despreze a resistência do ar.
v (m/s)
40
B
30
20
10
A
0
0,0
1,0
2,0
3,0
t(s)
27. (Vunesp-1996) A figura representa o gráfico velocidade x tempo do movimento retilíneo de um
móvel.
a) Qual o deslocamento total desse móvel?
b) Esboce o gráfico posição x tempo correspondente, supondo que o móvel partiu de origem.
28. (UFPE-1996) A velocidade de um objeto que se move ao longo de uma linha reta horizontal está
representada em função do tempo, na figura a seguir.
Qual o deslocamento escalar, em metros, do objeto após os primeiros 5 segundos?
29. (Fatec-2007) Dois móveis M e N partem de um mesmo ponto e percorrem a mesma trajetória.
Suas velocidades
variam com o tempo, como mostra o gráfico abaixo.
Analise as seguintes afirmações a respeito desses móveis.
I.
Os dois descrevem movimento uniforme.
II.
Os dois se encontram no instante t = 10 s.
III.
No instante do encontro, a velocidade de M será 32 m/s.
Deve-se afirmar que apenas
a) I é correta.
b) II é correta.
c) III é correta.
d) I e II são corretas.
e) II e III são corretas.
30. (Cesgranrio-1995) A casa de Dona Maria fica no alto de uma ladeira. O desnível entre sua casa
e a rua que passa no pé da ladeira é de 20 metros. Dona Maria tem 60kg e sobe a rua com velocidade
constante. Quando ela sobe a ladeira trazendo sacolas de compras, sua velocidade é menor. E seu
coração, quando ela chega à casa, está batendo mais rápido. Por esse motivo, quando as sacolas
de compras estão pesadas, Dona Maria sobe a ladeira em ziguezague. A ordem de grandeza do
gasto de energia, em joules, de Dona Maria, ao subir a ladeira é:
a) 103
b) 104
c) 105
d) 106
e) 107
31. (UNIFESP-2006) A figura representa o gráfico do módulo F de uma força que atua sobre um
corpo em função do seu deslocamento x. Sabe-se que a força atua sempre na mesma direção e
sentido do deslocamento.
Pode-se afirmar que o trabalho dessa força no trecho representado pelo gráfico é, em joules,
a) 0.
b) 2,5.
c) 5,0.
d) 7,5.
e) 10.
32. (Unifesp-2005) Avalia-se que um atleta de 60 kg, numa prova de 10000 m rasos, desenvolve
uma potência média de 300 W.
a) Qual o consumo médio de calorias desse atleta, sabendo que o tempo dessa prova é de cerca de
0,50 h? Dado: 1 cal = 4,2 J.
b) Admita que a velocidade do atleta é constante. Qual a intensidade média da força exercida sobre
o atleta durante a corrida?
33. (PUC - MG-2007) Considere um corpo sendo arrastado, com velocidade constante, sobre uma
superfície horizontal onde o atrito não é desprezível. Considere as afirmações I, II e III a respeito da
situação descrita.
I.
O trabalho da força de atrito é nulo.
II.
O trabalho da força peso é nulo.
III.
A força que arrasta o corpo é nula.
A afirmação está INCORRETA em:
a) I apenas.
b) I e III, apenas.
c) II apenas.
d) I, II e III.
34. (PUC-RJ-2001) Durante a Olimpíada 2000, em Sidney, um atleta de salto em altura, de 60 kg,
atingiu a altura máxima de 2,10 m, aterrissando a 3m do seu ponto inicial. Qual o trabalho realizado
pelo peso durante a sua descida? (g = 10 m/s²)
a) 1800 J
b) 1260 J
c) 300 J
d) 180 J
e) 21 J
35. (Vunesp-0) Na figura sob a ação da força de intensidade 2N, constante, paralela ao plano, o
bloco sobe 0,8 m ao longo do plano com velocidade constante. Admite-se g = 10 m/s2 , despreza-se
o atrito e são dados:
sen 30o = cos 60o = 0,5 e cos 120o = - 0,5.
Determine:
a) a massa do bloco
b) o trabalho realizado pelo peso do bloco, nesse percurso.
36. (Fuvest-1981) Quando uma pessoa de 70 kg sobe 2 m numa escada, ela realiza um trabalho
cuja ordem de grandeza é (adote g =10 m/s2 ) :
a) 10 J
b) 102 J
c) 103 J
d) 104 J
e) 105 J
37. (FEI-1996) Um aluno ensaiou uma mola pelo Método Estático e montou o gráfico a seguir. Qual
é o trabalho da Força Elástica para o deslocamento de 3 a 5m?
a) 20 J
b) 30 J
c) 50 J
d) 80 J
e) 150 J
38. (Vunesp-1995) Um bloco de madeira, de massa 0,40kg, mantido em repouso sobre uma
superfície plana, horizontal e perfeitamente lisa, está comprimindo uma mola contra uma parede
rígida, como mostra a figura a seguir.
Quando o sistema é liberado, a mola se distende, impulsiona o bloco e este adquire, ao abandonála, uma velocidade final de 2,0m/s. Determine o trabalho da força exercida pela mola, ao se distender
completamente:
a) sobre o bloco e.
b) sobre a parede.
39. (Vunesp-1994) Um carrinho desloca-se em linha reta sobre uma superfície plana e horizontal, às
custas da força
r
F constante, indicada em escala na figura a seguir.
r
a) Qual é o trabalho realizado pela força F , quando o carrinho se desloca do ponto P ao ponto Q,
distante 2,0 metros de P?
b) se tinha energia cinética de 4,0 J quando passou por P, dirigindo-se para Q, que energia cinética
terá ao passar por Q? (Despreze possíveis atritos)
40. (Ilha Solteira-2001) Deslocando-se por uma rodovia a 108 km/h (30 m/s), um motorista chega à
praça de pedágio e passa a frear o carro a uma taxa constante, percorrendo 150 m, numa trajetória
retilínea, até a parada do veículo. Considerando a massa total do veículo como sendo 1000 kg, o
módulo do trabalho realizado pelas forças de atrito que agem sobre o carro, em joules, é
a) 30 000.
b) 150 000.
c) 450 000.
d) 1 500 000.
e) 4 500 000.
41. (Gama Filho-1997) Para que um projétil de massa igual a 0,5 kg seja disparado com velocidade
de 80 m/s, é necessário imprimir-lhe uma energia cinética, em Joules, de:
a) 1,6 × 101
b) 1,6 × 102
c) 1,6 × 103
d) 1,6 × 104
e) 1,6 × 105
42. (Unicamp-1994) Sob a ação de uma força constante, um corpo de massa m = 4,0 kg adquire, a
partir do repouso, a velocidade de 10m/s, após percorrer 25 metros.
a) Qual é trabalho realizado por essa força?
b) Qual a potência média desenvolvida por esta força ?
43. (Unicamp-1994) Sob a ação de uma força constante, um corpo de massa m = 4,0kg adquire, a
partir do repouso, a velocidade de 10m/s.
a) Qual é trabalho realizado por essa força?
b) Se o corpo se deslocou 25m, qual o valor da força aplicada?
44. (UFU-2001) Um corpo de 10 kg desloca-se em uma trajetória retilínea, horizontal, com uma
velocidade de 3m/s, quando passa a atuar sobre ele uma força F, que varia de acordo com o gráfico,
formando um ângulo reto com a direção inicial do movimento. Se F é a única força que atua sobre o
corpo e se sua direção e sentido permanecem constantes, analise as seguintes afirmações e
responda de acordo com o código que se segue.
I.
II.
III.
A energia cinética do corpo no instante t = 6s é de 125 J.
O trabalho realizado pela força F no intervalo entre t = 0 e t = 6 s é nulo.
A quantidade de movimento do corpo no instante t = 6s é de 70 kg.m/s.
a) I e II são corretas.
b) Apenas I é correta.
c) II e III são corretas.
d) I e III são corretas.
45. (PUC-SP-1995) Um corpo de massa 0,3kg está em repouso num local onde a aceleração
gravitacional é 10m/s2. A partir de um certo instante, uma força variável com a distância segundo a
função: F = 10 - 20 •d (onde F está em newtons (N) e d em metros (m)) passa a atuar no corpo na
direção vertical e sentido ascendente. Qual a energia cinética do corpo no instante em que a força F
se anula?
(Despreze todos os atritos)
a) 1,0J.
b) 1,5J.
c) 2,0J.
d) 2,5J.
e) 3,0 J.
46. (PUC-Camp-1995) Um corpo de massa 12kg está submetido a diversas forças, cuja resultante
r
R é constante. A velocidade do corpo num ponto M é de 4,0m/s e num outro ponto N é de 7,0m/s.
r
O trabalho realizado pela força R no deslocamento de M para N é, em joules, de:
a) 33
b) 36
c) 99
d) 198
e) 396
GABARITO
1. Alternativa: C
2. Alternativa: B
4. a) SA = 0 + 6t
SB = 20 + 2t
b) t = 5 s
c) S = 30 m
5. a) V = 72 km/h
b) ∆S = 3 metros
6. Alternativa: E
7. a) ∆S = 5040 m
b) ∆t = 5,6 x 10-4s
8. Alternativa: D
9. a) SA = 0 + 15t
SB = 100 – 10t
b) t = 4 s
c) S = 60 m
d)
10. Alternativa: D
11. Alternativa: D
3. t = 15 s
12. a) d = 200 m
b) aproximadamente 1 h
13. a) S0 = 5 m ; V0 = -2 m/s ; a = 2 m/s2
b) V = -2 + 2.t
c) V = -2 + 2.(5) = 8 m/s
14. a) V0 = 30 m/s e a = −10 m/s2
b) V = − 10 m/s
c) sim, no instante t= 3 s
d) t = 2 s → mov. progressivo retardado
t = 4 s → mov. regressivo e acelerado
e)
15. Alternativa: D
16. Alternativa: A
17. Alternativa: C
18. Alternativa: A
19. Alternativa: E
20. Alternativa: C
21. Alternativa: C
22. Alternativa: D
23. Alternativa: D
24. Alternativa: B
25. a) a = 2 m/s2
b) ∆S = 100 m
26. d = 14 m
27. a) ∆S = 750 m
b)
28.
S = 12m
29. Alternativa: C
30. Alternativa: B
31. Alternativa: C
32. a) Q = 1,3 × 105 calorias
b) FM = 54 N
33. Alternativa: B
34. Alternativa: B
35. a) m = 0,4 kg
b)
τ P = − 1,6 J
36. Alternativa: C
37. Alternativa: D
38. a) τ = 0,80 J
b) o trabalho da mola sobre a parede é nulo, já que a parede não se desloca.
39. a) τ = 6 J
b) EC = 10 J
40. Alternativa: E
41. Alternativa: C
τF
= 200 J
42. a)
b) Pm = 40 W
43. a) τ = 200J
b) F = 8N
44. Alternativa: B
45. Alternativa: A
46. Alternativa: D