VELOCIDADE E ACELERAÇÃO VETORIAL

VELOCIDADE E
ACELERAÇÃO VETORIAL
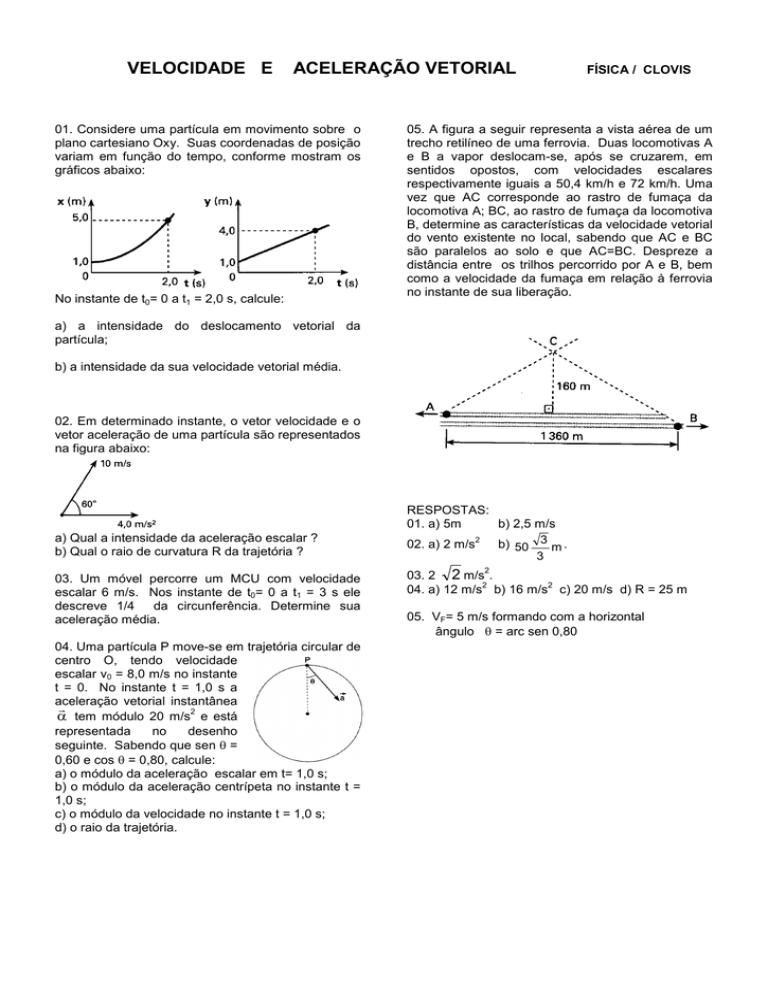
01. Considere uma partícula em movimento sobre o
plano cartesiano Oxy. Suas coordenadas de posição
variam em função do tempo, conforme mostram os
gráficos abaixo:
No instante de t0= 0 a t1 = 2,0 s, calcule:
FÍSICA / CLOVIS
05. A figura a seguir representa a vista aérea de um
trecho retilíneo de uma ferrovia. Duas locomotivas A
e B a vapor deslocam-se, após se cruzarem, em
sentidos opostos, com velocidades escalares
respectivamente iguais a 50,4 km/h e 72 km/h. Uma
vez que AC corresponde ao rastro de fumaça da
locomotiva A; BC, ao rastro de fumaça da locomotiva
B, determine as características da velocidade vetorial
do vento existente no local, sabendo que AC e BC
são paralelos ao solo e que AC=BC. Despreze a
distância entre os trilhos percorrido por A e B, bem
como a velocidade da fumaça em relação à ferrovia
no instante de sua liberação.
a) a intensidade do deslocamento vetorial da
partícula;
b) a intensidade da sua velocidade vetorial média.
02. Em determinado instante, o vetor velocidade e o
vetor aceleração de uma partícula são representados
na figura abaixo:
a) Qual a intensidade da aceleração escalar ?
b) Qual o raio de curvatura R da trajetória ?
03. Um móvel percorre um MCU com velocidade
escalar 6 m/s. Nos instante de t0= 0 a t1 = 3 s ele
descreve 1/4 da circunferência. Determine sua
aceleração média.
04. Uma partícula P move-se em trajetória circular de
centro O, tendo velocidade
escalar v0 = 8,0 m/s no instante
t = 0. No instante t = 1,0 s a
aceleração vetorial instantânea
r
a tem módulo 20 m/s2 e está
representada
no
desenho
seguinte. Sabendo que sen q =
0,60 e cos q = 0,80, calcule:
a) o módulo da aceleração escalar em t= 1,0 s;
b) o módulo da aceleração centrípeta no instante t =
1,0 s;
c) o módulo da velocidade no instante t = 1,0 s;
d) o raio da trajetória.
RESPOSTAS:
01. a) 5m
b) 2,5 m/s
2
02. a) 2 m/s
b) 50 3 m .
3
2
03. 2 2 m/s .
2
2
04. a) 12 m/s b) 16 m/s c) 20 m/s d) R = 25 m
05. VF= 5 m/s formando com a horizontal
ângulo q = arc sen 0,80