Prova comentada - Vestibular UFSC 2005

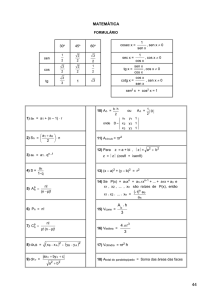
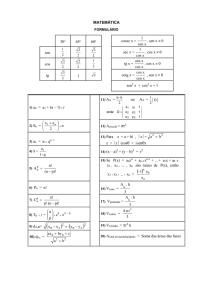
MATEMÁTICA
FORMULÁRIO
sen
30o
45o
60o
1
2
3
2
3
cos
2
3
tg
3
2
2
cosec x =
sec x =
2
1
2
2
1
3
tg x =
1
sen x
1
cos x
sen x
cotg x =
cos x
cos x
, sen x ≠ 0
, cos x ≠ 0
, cos x ≠ 0
sen x
2
, sen x ≠ 0
2
sen x + cos x = 1
10) A∆ =
b⋅h
ou
2
1) an = a1 + (n – 1) • r
onde D =
 a1 + a n 
•n
 2 
2) Sn = 
3) an = a1 • q
n –1
11) Acírculo = πr
A∆ =
x1
x2
y1 1
y2 1
x3
y3 1
1- q
2
2
2
12) (x – a) + (y – b) = r
(n − p)!
6) Pn = n!
p
8) dA,B =
9) dP,r =
n-1
x1 • x2 • ... • xn =
n!
p
7) C n =
D
13) Se P(x) = anx + an - 1x + ... + a1x + a0 e
x1 , x2 , ... , xn são raízes de P(x), então
a1
5) A n =
2
2
n
4) S =
1
14) Vcone =
A
15) Vpirâmide =
n!
p! (n − p)!
( x B − x A )2 + (y B − y A )2
ax 0 + by 0 + c
a 2 + b2
16) Vesfera =
b
•
h
3
A
b
•
3
4 π r3
3
2
17) Vcilindro = πr h
h
(- 1)n a 0
an
Questão 21
Tem-se uma folha de cartolina com forma retangular, cujos lados medem 56cm e 32cm e
deseja-se cortar as quinas, conforme ilustração
a seguir. Quanto deve medir x, em centímetros,
para que a área da região hachurada seja a
maior possível?
Assinale o resultado encontrado no cartãoresposta.
x
x
x
x
x
x
x
Questão 22
Em cada item a seguir, f(x) e g(x) representam leis de formação de funções reais f e g,
respectivamente. O domínio de f deve ser considerado como o conjunto de todos os valores
de x para os quais f(x) é real. Da mesma forma,
no caso de g considera-se o seu domínio todos
os valores de x para os quais g(x) é real.
Verifique a seguir o(s) caso(s) em que f e g
são iguais e assinale a(s) proposição(ões)
CORRETA(S).
01. f ( x) =
x 2 e g ( x) = x
02. f ( x) =
x 2 e g ( x) = x
04. f ( x) =
x
1
e g ( x) =
x
x
x
Gabarito: 11 (questão aberta)
Número de acertos: 896 (9,63%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
Para resolver esta questão, o vestibulando deveria seguir os seguintes passos:
Passo 1 - montar a equação matemática da
área da região dada na figura em função de
x: A = 2x(56 – 2x) + 2x(32 – 2x);
Passo 2 - uma vez obtida a equação, observar
que ela é a expressão, em R, de uma função
quadrática, cuja representação no plano cartesiano é uma parábola com concavidade voltada
para baixo;
Passo 3 - obter a ordenada do vértice.
A ordenada do vértice, x = 11 cm, é a resposta
que se esperava e foi dada por quase 10% dos
alunos.
Uma outra resposta, x = 8 cm, com uma
freqüência aproximada de 13% foi dada. É bem
provável que tal solução tenha sido proposta
por meio de uma medida feita diretamente sobre
o desenho fornecido na questão.
Esta questão, pelo caminho de solução
apresentado, não está sujeita a cálculos muito
trabalhosos e as atividades em cada um dos passos sugeridos são comuns no ensino em que este
assunto é tratado. É o encadeamento dos três
passos para chegar à solução que torna a questão
mais complexa.
08. f ( x) =
( x)
2
e g ( x) = x
x
e g ( x) =
x −1
16. f ( x) =
x
x −1
Gabarito: 05 (01 + 04)
Número de acertos: 257 (2,73%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
A proposição 08, dentre todas as demais,
foi a mais aceita como verdadeira pelos vestibulandos. Isto exemplifica um tipo de comportamento bastante observado em nossos alunos.
( )
2
No caso desta proposição, f ( x) = x
“a raiz quadrada é cortada com o quadrado” como um hábito, sem que se pergunte o domínio de
aplicação desta propriedade, fazendo com que
( )
2
f ( x) = x se torne igual a g(x) = x. Tal proposição é a que mais compôs as respostas dos
alunos, cerca de 63%.
Com freqüência um pouco menor, e de
forma semelhante, isto ocorreu também com as
proposições 02 e 16 desta questão.
Questão 23
Na figura a seguir, o segmento de reta AE é
paralelo ao segmento BF e o segmento de reta
CG é paralelo ao segmento DH; o trapézio
ABDC tem os lados medindo 2cm, 10cm, 5cm e
5cm, assim como o trapézio EFHG; esses
trapézios estão situados em planos paralelos
que distam 4cm um do outro. Calcule o volume
3
(em cm ) do sólido limitado pelas faces ABFE,
CDHG, ACGE, BDHF e pelos dois trapézios.
Assinale o resultado encontrado no cartãoresposta.
F
E
B
A
H
G
C
D
Gabarito: 72 (questão aberta)
Número de acertos: 1.719 (18,51%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Uma dificuldade que ela apresenta, e que
pode ser a mais significativa, reside na passagem
dos dados do texto, que é longo, para a figura
auxiliar fornecida. Isso implica na visualização
global da imagem que automaticamente solicita
o raciocínio, ou seja, é preciso ver na figura dada
a decomposição de outras figuras geométricas,
tais como os trapézios, além da decomposição
desses trapézios para fins de cálculos. Contudo,
esta questão é bastante típica do ensino médio, o
que leva ao reconhecimento, por parte dos candidatos, dos passos para a solução.
Questão 24
Assinale a(s) proposição(ões) CORRETA(S).
2
01. (30%) = 0.09.
80%
= 40% .
02.
2%
04. As promoções do tipo "leve 5 e pague 4", ou
seja, levando-se um conjunto de 5 unidades, paga-se o preço de 4, acenam com um
desconto sobre cada conjunto vendido de
25%.
08. Uma pedra semipreciosa de 20 gramas caiu
e se partiu em dois pedaços de 4g e 16g.
Sabendo-se que o valor, em uma certa unidade monetária, desta pedra é igual ao
quadrado de sua massa expressa em gramas, a perda é de 32% em relação ao valor
da pedra original.
16. Um
quadro
cujo preço
de
custo
era
R$ 1.200,00 foi vendido por R$ 1.380,00.
Neste caso, o lucro obtido na venda, sobre
o preço de custo, foi de 18%.
Gabarito: 09 (01 + 08)
Número de acertos: 2.004 (21,29%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Um contingente de alunos (9,85%), bastante significativo, assinalou como verdadeira
apenas a proposição 01. Compondo outras respostas, essa proposição tem um percentual próximo de 75%. Enquanto que a proposição 08,
também verdadeira, na composição das respostas
alcança um percentual de 52%, aproximadamente. O conteúdo matemático solicitado nesta questão envolve, basicamente, a noção de porcentagem. Considera-se tal noção bastante presente no
quotidiano dos alunos, o que poderia levar os
candidatos a aproximar seus conhecimentos escolares aos seus conhecimentos de uso fora da
escola.
Questão 25
Assinale a(s) proposição(ões) CORRETA(S).
01. O vigésimo termo da progressão aritmética
2
(x, x +10, x , ...) com x < 0 é 186.
02. A soma dos n primeiros números naturais
2
ímpares é n + 1.
04. O
valor
de
x x
x + + + ... = 12 , na
3 9
x
na
qual
igualdade
o
primeiro
membro é a soma dos termos de uma PG
infinita, é 10.
08. Sabendo que a sucessão (x, y, 10) é uma
PA crescente e a sucessão (x, y, 18) é uma
PG crescente, então xy = 12.
16. O termo
1
encontra-se na décima se1024
gunda posição na progressão geométrica
2, 1,
1
, ... .
2
Gabarito: 25 (01 + 08 + 16)
Número de acertos: 804 (8,56%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
A questão 25 compreende 5 proposiçõesquestões típicas do ensino médio, envolvendo os
conteúdos sobre Progressões. Observa-se um
bom índice de acertos parciais em 16 e 24 (16 e
08 simultaneamente), um pouco acima de 12%
em ambos os casos. A proposição correta 16 foi
a que mais compôs as respostas dos alunos, cerca
de 68%. Em seguida vem a proposição correta
08, com aproximadamente 59%.
Questão 26
Um projétil é lançado verticalmente para cima
com velocidade inicial de 300m/s (suponhamos
que não haja nenhuma outra força, além da
gravidade, agindo sobre ele). A distância
d (em metros) do ponto de partida, sua velocidade v (em m/s) no instante t (em segundos
contados a partir do lançamento) e aceleração
a (em m/s2) são dadas pelas fórmulas:
d = 300 t -
1
× 10t2, v = 300 - 10t, a = - 10
2
Assinale a(s) proposição(ões) CORRETA(S).
01. O projétil atinge o ponto culminante no instante t = 30s.
02. A velocidade do projétil no ponto culminante
é nula.
04. A aceleração do projétil em qualquer
2
ponto da sua trajetória é a = - 10m/s .
08. O projétil repassa o ponto de lançamento no
instante t = 60s.
16. A distância do ponto culminante, medida a
partir do ponto de lançamento, é de 4 500m.
32. O projétil repassa o ponto de partida
com velocidade v = 300m/s.
Gabarito: 31 (01 + 02 + 04 + 08 + 16)
Número de acertos: 407 (4,33%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
O que ressalta nesta questão é o número
significativo de alunos que considerou correta a
proposição 32. Tal proposição afirmava que: “O
projétil repassa o ponto de partida com velocidade v = 300m/s”. A proposição correta 02 foi a
que mais compôs as respostas dos alunos, cerca
de 80%. Em seguida, vem a proposição correta
01, com aproximadamente 70%.
Interessante dizer que esta questão constitui-se, na verdade, numa contextualização de
equações, exigindo do aluno a substituição de
dados numéricos na equação e o entendimento
gráfico da situação contextualizada.
Questão 27
Considere um triângulo eqüilátero cujo lado mede 12cm de comprimento e um quadrado em
que uma das diagonais coincida com uma das
alturas desse triângulo. Nessas condições, de2
termine a área (em cm ) do quadrado.
Assinale o resultado encontrado no cartãoresposta.
Gabarito: 54 (questão aberta)
Número de acertos: 2.201 (23,55%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Esta questão envolve a noção de área e
aplicação do Teorema de Pitágoras. Possivelmente sua maior dificuldade esteja em transformar o texto do enunciado no desenho geométrico
correspondente que possibilite encontrar a área
da figura solicitada.
A resposta correta obteve 23,55%. Há
também 1.385 (14,82%) para a resposta 36 e 828
(8,86%) para 72 que podem caracterizar o uso
meramente manipulativo de números presentes
no enunciado da questão.
Questão 28
Qualquer que seja o
ce à relação n ≤ x
mero inteiro. Diz-se
de x e é denotada
04. A soma dos elementos da inversa da
número real x, ele obede< n + 1, sendo n um núque n é a parte inteira
por E(x) = n.
A partir dessa definição de E, calcular Y na
expressão:
Y=
(
(
)
)
4 x E 299 + 2 x E log 127 − E (sen233°)
5
( )
7 
E  + E 2
8
Gabarito: 75 (questão aberta)
Número de acertos: 120 (1,30%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
Esta questão solicita dos alunos um fato
que, habitualmente, o ensino não leva muito em
consideração, ou seja, a compreensão com precisão de uma definição. Sendo assim, os cálculos
requeridos na questão são muito poucos, mas o
domínio da definição dada associada a conhecimentos matemáticos é essencial para resolver a
questão. A resposta correta obteve apenas 1,30%
e pelo fato de que muitos alunos consideraram
E(sen 233o) = 0 no lugar de E(sen 233o) = -1, a
resposta 74 obteve 4,74% de acertos.
Questão 29
Assinale a(s) proposição(ões) CORRETA(S).
01. Se as matrizes P, Q e R são escolhidas entre as listadas a seguir, para que PQ – R
seja uma matriz nula, o valor de x deve
ser 2.
6
0

−1
2
0 0 1


que a matriz 0 0 0 é anti-simétrica.


1 0 0 
1
x

,

 x + 2y = 9
3x + 6y = 27
ção do sistema 
32. A e B são matrizes quadradas de ordem 2
tais que A = 5B. Nestas condições podese afirmar que det(A) = 5det(B), sendo que
det(A) e det(B) designam, respectivamente,
os determinantes das matrizes A e B.
ANÁLISE DA QUESTÃO
[3x 5] ,
08. Uma matriz quadrada A se diz anti-simétrica
t
t
se A = -A, sendo A a transposta da matriz A. Nessas condições pode-se afirmar
16. O par ordenado (x, y) = (5, 2) é a única solu-
Assinale o resultado encontrado no cartãoresposta.
3
1 ,
 
2 
1 1
 é igual a 2.
0 1
matriz 
19 
6 
 
02. A matriz A = (aij)1×3, tal que aij = i –3j é
A = [− 2 − 5 − 8 ] .
Gabarito: 03 (01 + 02)
Número de acertos: 480 (5,10%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
Esta questão envolve 6 proposiçõesquestões sobre matrizes, típicas de ensino médio.
Observa-se um percentual bastante significativo
de alunos que assinalaram como verdadeira apenas a proposição 02 (14,40%). Esta proposição
foi a que mais compôs as respostas dos alunos,
cerca de 68%.
A proposição 01, que também é verdadeira, compôs, apenas, em torno de 20% das respostas. Nesta proposição talvez a maior dificuldade
resida no fato de que a equação matricial necessita ser montada.
Questão 30
Sejam a e b os ângulos centrais associados,
respectivamente, aos arcos AN e AM na circunferência trigonométrica da figura 1 e considere x na figura 2, a seguir. Determine o
4
valor de y = 15x , sabendo que a + b =
π
.
2
Assinale o resultado encontrado no cartãoresposta.
OA = 1
N
M
O
P Q
A
Figura 1
x
OP + OQ
•
PN − QM
Figura 2
Gabarito: 60 (questão aberta)
Número de acertos: 1.311 (14,19%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
Observa-se que 1.712 (18,54%) alunos
assinalaram a resposta 15, possivelmente considerando x = 1 na fórmula Y = 15x4. Qualquer
outro número inteiro maior do que 1 para x resulta, para Y, em um número inteiro fora do limite de resposta possível.
Novamente é a simples manipulação superficial de números que comanda de forma significativa a resposta de muitos alunos.