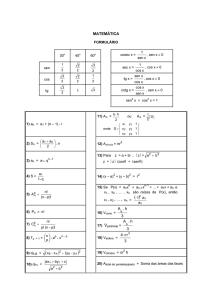
MATEMÁTICA
FORMULÁRIO
sen
30o
45o
60o
1
2
3
2
2
3
cos
2
2
3
tg
2
3
1
cosec x =
sec x =
2
1
tg x =
2
cotg x =
3
1
sen x
1
cos x
sen x
, sen x 0
, cos x 0
, cos x 0
cos x
cos x
sen x
, sen x 0
sen2 x + cos2 x = 1
11) A =
bh
ou
A =
2
2
1) an = a1 + (n – 1) r
onde
a1 a n
n
2
D
x1
x2
y1 1
y2 1
x3
y3 1
D
12) Acírculo = r2
2) Sn =
13) Para
3) an = a1 qn –1
4) S =
1
z = a + bi , z = a 2 b 2
z = z (cos + i sen)
a1
14) (x – a)2 + (y – b)2 = r2
1- q
15) Se P(x) = anxn + an - 1xn -1 + ... + a1x + a0 e
x1 , x2 , ... , xn são raízes de P(x), então
n!
p
5) A n
(n p)!
x1 x2 ... xn =
A
6) Pn = n!
7) C n
16) Vcone =
17) Vpirâmide =
p! (n p)!
an
h
3
A
n!
p
b
- 1n a 0
b
h
3
[
n p n p
8) Tp + 1 = a x
p
9) dA,B=
10) dP,r =
x B x A 2 yB yA 2
ax 0 by 0 c
a b
2
2
18) Vesfera =
4 π r3
3
19) Vcilindro = r2 h
20) Atotal do paralelepípedo = Soma das áreas das faces
21) Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
01. Um subconjunto A dos números reais será denominado intervalo
quando a implicação "(a, b A e a < x < b) (x A)" for
verdadeira.
02. A representação dos pontos do plano através de pares
ordenados de números reais
(x, y) deve estar sempre
referenciada a um sistema de eixos ortogonais.
04. É possível obter uma bijeção entre o conjunto dos números
naturais e o conjunto dos números inteiros.
08. É possível obter uma bijeção entre o conjunto dos números
naturais e o conjunto + dos números racionais positivos.
16. Se a < b são dois números racionais existem sempre x racional e
y irracional com a < x < b e a < y < b.
Gabarito: 29 (01 + 04 + 08 + 16)
Número de acertos: 48 (0,54%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
Apesar da questão ter se mostrado difícil, pois apenas 0,54% dos
candidatos a responderam corretamente, a soma dos acertos parciais
atingiu 32,92%, revelando que a dificuldade de cada proposição
separadamente não foi tão grande.
Chama a atenção nessa questão que a proposição incorreta (02)
tenha sido assinalada por 5.881 candidatos, o que representa um
percentual de 66,08%. Aparentemente foi este o motivo de ter havido
um número tão reduzido de acertos nesta questão. Isso faz crer que
no Ensino Médio não se faça referência a outros sistemas, além do
sistema cartesiano ortogonal, pela grande maioria dos professores.
Simplesmente lamentável.
22) Assinale no cartão-resposta a soma dos números associados à(s)
proposição(ões) CORRETA(S).
01. Obter 7 acertos numa prova de 12 questões é um desempenho
inferior a obter 6 acertos numa prova de 10 questões, porém
superior a obter 5 acertos numa prova de 9 questões.
02. Um investidor tem seu dinheiro aplicado a 2% ao mês. Deseja
comprar um bem no valor de R$ 100.000,00, que pode ser pago
a vista ou em três parcelas de R$ 34.000,00, sendo a primeira de
entrada e as outras em 30 e 60 dias. Ele sairá lucrando se fizer
a compra parcelada.
04. Duplicando-se o lado de um triângulo eqüilátero, sua área fica
também duplicada.
08. Se 2 impressoras trabalhando 10 horas por dia levam 5 dias para
fazer determinado trabalho, então 3 impressoras (com a mesma
eficiência das anteriores) trabalhando 8 horas por dia levarão 6
dias para fazer o mesmo trabalho.
Gabarito: 01 (01)
Número de acertos: 1.582 (17,84%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Considerando que 5.093 candidatos (57,23%) assinalaram a
proposição 01, pode-se concluir que essa proposição isoladamente se
mostrou fácil, porém, observando que desses, apenas 1.582 candidatos assinalaram unicamente essa proposição, conclui-se que a questão
como um todo apresentou um grau médio de dificuldade. Porém, nos
causa admiração verificar que 12,14% responderam que a proposição
01 e 02 estão corretas. A proposição 02 trata de um simples cálculo
com juros normais para o nosso cotidiano. É simplesmente absurdo.
23) Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
01. O valor de sen
9
2
é 1.
02. O gráfico da função g(x) = ln x2 é simétrico em relação ao eixo
das ordenadas.
04. Para todo arco x vale sen2x + cos2x = 1 e |senx| + |cosx| 1 e
pode ocorrer senx + cosx = 0.
08. Para todo arco x para o qual as expressões
cos x
1 tg x
e
1
sen x cos x
podem ser calculadas, elas forne-
cem o mesmo valor.
16. A imagem da função
y 3 cos x é o intervalo [3, 3].
Gabarito: 23 (01 + 02 + 04 + 16)
Número de acertos: 149 (1,68%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Apesar de ter havido apenas 1,68% de acertos absolutos, o fato de
70,61% dos candidatos terem obtido acerto parcial revela que o grau
de dificuldade apresentado pela questão foi no máximo médio.
24) Sejam (an) uma progressão geométrica e (bn) uma progressão
aritmética cuja razão é
3
da razão da progressão geométrica
10
(an).
Sabendo que a1 = b1 = 2 e que a2 = b7 calcule a soma
b1 + b2 + ... + b7.
Assinale o resultado encontrado no cartão-resposta.
Gabarito: 77 (Aberta)
Número de acertos: 1.589 (18,19%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Freqüências é um conteúdo normalmente bem trabalhado no
Ensino Médio. Isso podemos observar nesta questão, considerada
difícil pela Banca, porque envolve P.A. e P.G. simultaneamente; no
entanto houve um número razoável de acertos.
25) Suponha que em uma determinada espécie de animais os
indivíduos tenham seus primeiros filhotes aos 8 meses, e que a
partir de então para cada adulto da população nasçam, em
média, 3 filhotes a cada 3 meses. Se no início de janeiro
nascerem os primeiros 12 filhotes de 4 indivíduos com os quais
se esteja iniciando uma criação, qual será o número provável de
indivíduos que a população atingirá no início de outubro, não
havendo mortes?
Assinale o resultado encontrado no cartão-resposta.
Gabarito: 88 (Aberta)
Número de acertos: 1.291 (14,66%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Historicamente a análise combinatória é um conteúdo considerado difícil. Podemos observar que a questão, de nível médio, poderia
ser classificada como difícil pelo número de acertos.
26) Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
1
4
01. A matriz
5
3
2
3
0
2
5
1
não possui inversa.
4 8 1
1 2 0
02. Se um sistema de equações é indeterminado, então não se pode
encontrar solução para ele.
2
4
1
04. A solução da equação 2
4
x
3
1
2
= 0 é x = 1.
08. Uma pequena indústria produz três tipos de produto que indicamos por x, y, z. As unidades vendidas de cada produto e o
faturamento bruto da empresa em três meses consecutivos são
os dados na tabela abaixo. Então, os preços dos produtos x, y
e z só podem ser, respectivamente, R$ 1.000,00, R$ 5.000,00
e R$ 3.000,00.
Unidades Unidades Unidades
Faturamento
Mês
de x
de y
de z
bruto
vendidas vendidas vendidas
1
1
5
3
R$ 35.000,00
2
4
1
2
R$ 15.000,00
3
5
6
5
R$ 50.000,00
Gabarito: 05 (01 + 04)
Número de acertos: 488 (5,51%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
ANÁLISE DA QUESTÃO
Chama a atenção que a proposição incorreta 08 tenha sido
assinalada com maior freqüência: 6.106 candidatos (68,61%). Essa
proposição apresenta uma das soluções de um sistema de equações
indeterminado, que foi considerado por esses candidatos como a
única solução do sistema.
Esse erro sugere que nos Ensinos Fundamental e Médio esses
sistemas não estão sendo analisados com o devido cuidado.
27) Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
01. O polinômio 2x3 + 5x2 x 6 é divisível por x 1 e também
por 2x + 3.
02. O polinômio p(x) = x3 + x2 + 4x + 4 não pode ser escrito como
um produto de polinômios de grau 1 com coeficientes reais.
1
3
x2
x 2
1
04. A inequação
tem solução S = .
9
08. A solução da equação sen x tg x é constituída dos arcos x
para os quais sen x = 0 ou cos x = 1.
Gabarito: 11 (01 + 02 + 08)
Número de acertos: 565 (6,38%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Somando os percentuais dos acertos totais (6,38%) e dos parciais
(54,28%) obtém-se 60,66%, o que sugere que a questão de fato foi
fácil ou apresentou, no máximo, um grau médio de dificuldade.
O percentual de 54,28% dos acertos parciais revela a preocupação
dos candidatos em não assinalar proposições incorretas.
28) Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
01. Se a altura de um triângulo retângulo relativa ao ângulo reto
dividir a hipotenusa em segmentos de 3cm e 12cm, então a área
desse triângulo é de 45cm2.
02. A única maneira de provar que a soma dos ângulos internos de
um polígono convexo de n lados é Sn = (n – 2).180o consiste
em traçar todas as diagonais desse polígono que tenham origem
num vértice fixado, o que dividirá o polígono em n 2 triângulos.
04. Se o perímetro do quadrado inscrito numa circunferência é de
8cm então a área do quadrado circunscrito a essa circunferência
é de 8cm2.
08. Num pentágono regular, as diagonais traçadas de um mesmo
vértice formam entre si um ângulo de 40o.
Gabarito: 05 (01 + 04)
Número de acertos: 729 (8,23%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Observando a soma dos percentuais 8,23% + 17,02% = 25,25% e
levando em consideração o medo de assinalar proposições incorretas,
pode-se dizer que a questão apresentou, como previsto, um grau
médio de dificuldade.
O grande erro observado nesta questão foi que a proposição
incorreta 02 registrou a maior freqüência: 4.769 candidatos (53,59%).
Essa proposição versa sobre a demonstração da fórmula da soma dos
ângulos internos de um polígono convexo: Sn = (n – 2).180o.
29) Considere a circunferência C:
x 42 y 32 16
e a reta
r: 4x + 3y 10 = 0.
Assinale no cartão-resposta a soma dos números associados
à(s) proposição(ões) CORRETA(S).
01. A circunferência C intercepta o eixo das abscissas em 2 (dois)
pontos e o das ordenadas em 1 (um) ponto.
02. O centro de C é o ponto (3, 4).
04. r C = .
08. A distância da reta r ao centro de C é menor do que 4.
16. A função y dada pela equação da reta r é decrescente.
Gabarito: 25 (01 + 08 + 16)
Número de acertos: 760 (8,58%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Observando a soma 8,58% + 36,32% = 44,90% e levando em
consideração o medo de assinalarem proposições incorretas, pode-se
dizer que a questão apresentou, no máximo, um grau médio de
dificuldade, para os candidatos.
30) A geratriz de um cone eqüilátero mede 2 3 cm.
Calcule a área da seção meridiana do cone, em cm2, multiplique
o resultado por
3 e assinale o valor obtido no cartão-resposta.
Gabarito: 09 (Aberta)
Número de acertos: 1.435 (16,42%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
ANÁLISE DA QUESTÃO
Trata-se de uma questão aberta sobre geometria espacial e a
resposta mais assinalada foi a correta.
CONCLUSÃO
Observa-se que, de um modo geral, os candidatos têm a
preocupação de não assinalar proposições incorretas a fim de não
perder eventuais acertos parciais. Registramos esse fato como
positivo, mas se não fosse essa preocupação, certamente o nível de
acertos seria um pouco mais elevado.