Trabalho Grupo 12 - Métodos Matemáticos

Universidade Federal Fluminense
GMA
Métodos matemáticos 1
Professor: Altair
“Convergência e série dupla de fourier”
Alunos:
Leonardo Chaves da Costa
Rafael Dias Barreto
Rafael Sanches Rangel
Henrique Pereira Góes
Leonardo Nunes Vertulli
14/10/2010
Niterói – RJ
2010
Série Dupla de Fourier
Diz-se que uma função é contínua por partes num retângulo R do plano se:
i.
f é contínua no interior e no bordo de R, com a possível excessão de um número finito
de pontos, ou ao longo de um número finito de arcos difirenciáveis simples, ou em
ambos.
ii.
quando (xₒ, yₒ) é um ponto de descontinuidade de f e (x, y)
Existe
tende a (xₒ,yₒ) pelo interior de qualquer uma das regiões em que R é dividida pelos
arcos de descontinuidade
.
.
=
Extensão:
.
Teorema: Sejam
e {gj(y)} bases ortogonais dos espaços euclidianos CP[a,b] e CP[c,d],
respectivamente. Então, {fi(x,y) gj(x,y)}, i=1,2,... j=1,2,... é uma base de CP(R), onde R é o
retangulo
,
Série Dupla de Fourier Abaixo:
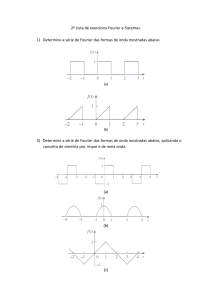
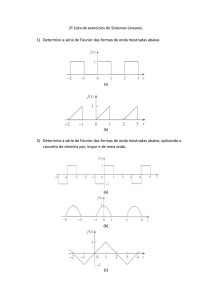
1) Base para CP[-π,π],
2) Base para CP[-π,π],
Assim:
3) Base para CP[-π,π]
3.1) Cálculo dos coeficientes de fourier:
Assim,
Onde, ‖cos (ix).cos (jy)‖² =
Ex.: F(x,y) = xy




De um modo mais geral, o conjunto de funçõe
é uma base do espaço euclidiano das funções contínuas por partes np retângulo
Teorema: Seja R o retângulo
,
contínua em R, e que
, e suponhamos que F seja
existam e sejam limitados em R. Então, a série
dupla de Fourier de F converge pontualmente para F em R.
Convergência das Séries de Fourier
I – CONVERGÊNCIA EM MÉDIA:
Em um espaço de funções com produto interno expresso por uma integral, a
afirmação segundo a qual
b
1/2 
lim f k  f  lim    f k  x   f  x    0
k 
k 
a

Não é o mesmo que dizer que a seqüência  f k  converge para função f em todo ponto
de  a, b (convergência pontual). Em análise matemática essa convergência via produto
interno é conhecida como convergência em média, para enfatizar que ela é calculada por
integração, que em certo sentido é um processo de média generalizado.
Ex: A seqüência de funções
 x, x , x ,...
2
3
converge em média para zero em e
1,1 (espaço das funções contínuas no intervalo fechado 1,1 ).
De fato,
1/2
 1 2k 
lim x  0  lim   x dx 
k 
k 
 1

1/2
 2 
lim 
 0
k  2k  1


2
3
Entretanto,  x, x , x ,... não converge para zero em cada ponto.
k
O exemplo dado mostra que a convergência em média é diferente da pontual.

DEFINIÇÃO: Diz-se que uma séries infinita
û
k 1
k
de vetores de um espaço
euclidiano converge para o vetor û  a seqüência associada das somas parciais
converge para û no sentido que lim û k  û  0 .
k 
Se este é o caso, escrevemos:

û   ûk
k 1
E dizemos que û foi desenvolvida em série infinita.

Mais detalhadamente,
û
k 1
k
converge para û  para cada número real   0
existe um inteiro K tal que
N
û
k
k 1
û  
Toda vez que N  K . O real  pode ser entendido como o “erro”. Na verdade
N
û
k 1
k
 û é a “distância” da soma ao vetor û. É sabido que todo espaço euclidiano de
dimensão finita tem uma base ortonormal û1 , û2 , û3 ,..., ûn e que todo vetor deste espaço
pode ser escrito de modo único sob a forma:
û  û.û1  û1  ...  û.ûN  ûN
É possível generalizar este resultado para espaços euclidianos de dimensão infinita.
Assim:
û   û.û1  û1  ...   û.ûN  ûN  ...
Ou

û    û.ûk  ûk
k 1
Entretanto sem informações mais detalhadas não existe, evidentemente nenhuma
garantia que esta série convirga para û. É claro que se converge (e isto ocorre em

inúmeras situações), justifica-se ecrever û    û.ûk  ûk , e dizemos que a série
k 1
comverge em média para û.
Os produtos internos  û.ûk  se denominam de coordenadas ou coeficientes de
Fourier (generalizados) de û em relação a base (ou conjunto ortonormal) û1 , û2 , û3 ,... . É
comum escrever:

û ~   û.ûk  ûk ,
k 1
Onde o símbolo ~ é para ressaltar que a série em questão pode não convergir para û.
Caso convirga justifica-se usar o símbolo de igualdade.

TEOREMA: Seja
a û
k 1
qualquer série infinita que converge em média para û,
k k

isto é, û   ak ûk . Então, ak  û.ûk para cada inteiro k.
k 1
É claro que se a série converge em média para û vale escrever:
N
lim û   ak ûk  0
N 
k 1
Se o espaço euclidiano em tela for cp  a, b deve-se entender û como f  x  , ak com
 a   , b   
AN e BN e ûk como sin( Nx) e cos( Nx)
(se f periódica de período
2 ).
DESIGUALDADE DE BESSEL: IGUALDADES DE PARSEVAL
TEOREMA: Seja û1 , û2 , û3 ,... um conjunto ortonormal de vetores de um espaço
euclidiano de dimensão infinita, e seja û um vetor arbitrário deste espaço, então:

  û.û 
k
k 1
2
 û
2
Esta expressão é chamada de desigualdade de Bessel. Além disso, û1 , û2 , û3 ,... é um base
do espaço em questão 

  û.û 
k 1
k
2
 û
2
, que é a igualdade de Parseval. No caso das
séries de Fourier a igualdade de Parseval é dada por


2
a
1
2
f    f  x   dx  0    ak 2  bk 2 
 
2 k 1
(Demonstração em III)
TEOREMA: Seja f uma função continuamente diferenciável por partes em cp[pi,pi] (f tem uma derivada primeira contínua por partes em [-π,π]). Então, o
desenvolvimento em série de Fourier de f converge pontualmente em [-π,π] e tem o
valor
π. Note
f(x)= +
média para f.
que
em cada ponto
do interior do intervalo, e
ao escrevermos a série de Fourier
de
f
em +como
significa que a série em questão converge em
→0 ou seja,
f(x)=
+
(média)
Ressaltamos que a convergência em média não significa que a série converge
pontualmente no sentido que:
F(
+
para todo
em [- ,π].
Contudo, o teorema apresentado explicita sob que condição a convergência
pontual ocorre, ou seja, o desenvolvimento em série de Fourier de uma função fєCP[π,π], continuamente diferenciável por partes converge, de fato para f( ) quando
é
um ponto de continuidade de f, ou seja, converge na reta inteira.
TEOREMA: Seja f uma função contínua em (- , ), com período 2π, e
considere que f tenha derivada primeira contínua por partes. Então, a série de Fourier de
f converge uniforme e absolutamente para f em todo intervalo fechado de x.
Se f for continuamente diferenciável por partes em (- , ) com período 2π. Então, a
série de Fourier converge uniformemente para f e qualquer intervalo fechado do eixo x
que não contenha ponto de descontinuidade de f.
DERIVAÇÃO E INTEGRAÇÃO DE SÉRIES DE FOURIER
TEOREMA: Seja f uma função contínua em (- , ), com período 2π, e
considere que f tenha derivada primeira f´ contínua por partes. Então, a série de Fourier
de f´ pode ser obtida derivando a série de f termo a termo, e a série derivada de f
converge pontualmente para f´(x) se f”(x) existe .
Ou seja,
Se F(
F’(
+
(f(x))=
(
=
(
=
=
→
f’(x)=
TEOREMA: Seja f uma função contínua por partes em (a série de Fourier de f:
F(
Então,
,
) com período 2π, e seja
+
=
Em outras palavras, a integral definida de f, de a a b, pode ser calculada, integrando-se a
série de Fourier de f termo a termo.
No caso de integral indefinida fica (teorema da integração):
Seja f uma função arbitrária de cp[-π, ] com série de Fourier
F(
+
Então a função
, -π<x<π tem uma série de Fourier que converge pontualmente
com relação a todo x do intervalo (-π, π), e
=
+
Pode-se entender que
=
,
=
III – IGUALDADE DE PARSEVAL:
Se f é uma função qualquer de cp[-π, π] então:
Onde ak e bk são os coeficientes de Fourier.
De fato:
Multiplicando (no sentido de produto interno) equação (1) por f obtém-se:
Tendo em vista que:
Conclui-se que:
E
Assim,
OBS: Em geral,
(desigualdade de Bessel),
Onde ê1, ê2, ... é um conjunto ortogonal de vetores de um espaço de dimensão infinita
(espaço euclidiano) V. Assim, x é um vetor arbitrário de V. Além disso, ê1, ê2, ... é uma
base de V se, e somente se,
(igualdade de Parseval).
FENÔMENO DE GIBBS
As somas parciais das séries de Fourier tendem a ir além dos valores de função
próxima a um ponto de descontinuidade
Assim, os valores de f(x) entre duas descontinuidades quaisquer estão no intervalo (ð/2, ð/2), enquanto que os de Sn(x) a N-ésima soma parcial percorrem um intervalo um
pouco maior, [-αn, αn]. O valor limite de n quando N →
determina aquele que é
conhecido como o intervalo de Gibbs de f.
CONVERGÊNCIA UNIFORME
TEOREMA DE WEIERSTRASS:
Se
é uma série convergente de números reais positivos e se
é uma
série de funções tais que
para todo k e todo x no intervalo a<x<b, então
é uniforme e absolutamente convergente em a<x<b.
Obs: se
converge, diz-se que a sérue converge absolutamente.
Obs2: Diz-se que uma sequência {
converge uniformemente para a função f(x)
no intervalo a<x<b, se qualquer que seja ɛ>0. existe inteiro positivo k, dependendo de ɛ,
mas não de x, tal que
quando K>K. e x está no intervalo dado.
Note que se {
for a sequência das somas parciais {
a série
correspondente converge uniformemente.
Quando k>K →
→0, para todo x
Quando K →
>
=
“coincide” exatamente com f(x) para
todo x є[a,b]. A convergência uniforme é “global”.
Obs: A sequência {
é construída a partir da sequência {
para o caso da
série de Fourier.
(
Ou seja,
(x)=
(x)=
+
.
.
.
(x)=
+
+...+
→
(
=f(x) (Série de Fourrier)
Aplicações:
As séries duplas Fourier têm muitas aplicações em disciplinas
científicas — em Física, Física e Química Quântica, Teoria dos números,
Análise combinatória, Processamento de sinal, Processamento de imagem,
Teoria das probabilidades, Estatística, Criptografia, Acústica,
Oceanografia, Sísmica, Óptica, Geometria e outras áreas. Nos campos
relacionados com o processamento de sinal, a série de Fourier é
tipicamente utilizada para decompor um sinal nas suas componentes em
frequência e suas amplitudes.
Na indústria naval-mecânica podemos encontrar aplicações para as
séries duplas de Fourier no estudo de vibrações em chapas e estruturas
metálicas, com o objetivo de encontrar e prevenir defeitos causados por
más formações que podem tornar a chapa quebradiça e insegura para o uso.
No ramo da engenharia elétrica e de telecomunicações as séries
duplas de Fourier têm papel fundamental na formação e representação de
funções de sinais de transmissão essenciais. Esta ferramenta matemática é
muito aplicada no processamento de sinais analógicos periódicos ou não.
Podemos comprovar então que as séries de Fourier são
indispensáveis nas resoluções de problemas que surgem no cotidiano das
ciências exatas sendo de grande valia seu aprendizado e domínio prático.
Referência:
Física Matemática; E. Butcov;
Equações Diferenciais e problemas de contorno; C. Boyce;
Apostilas de Métodos Matemáticos;
Wikipédia;