Planejamento de Trajetórias - Instituto de Engenharia Mecânica

Universidade Federal de Itajubá - UNIFEI
Instituto de Engenharia de produção e Gestão - IEPG
EPR-03 Automação da Manufatura
Notas sobre:
Planejamento de
Trajetórias
Y
L2
(x, y)
L1
X=L1.C1+L2.C12
Y=L1.S1+L2.S12
θ2
X=L1.C1
Y=L1.S1
θ1
X
X=0
Y=0
Prof. José Hamilton Chaves Gorgulho Júnior
Itajubá - Outubro de 2009
Revisão 0
1
Planejamento de Trajetória
INTRODUÇÃO
O planejamento de trajetória é realizado pelo programa de controle de um robô para
calcular a posição de cada junta, a cada instante, permitindo que o órgão terminal movimentese segundo a trajetória programada. Aparentemente os cálculos envolvem apenas as
coordenadas inicial e final, mas os artigos irão mostrar que são necessários cálculos que
envolvem cinemática direta, cinemática inversa, coordenadas intermediárias, velocidade,
aceleração e também o tempo de deslocamento.
CONCEITOS BÁSICOS
Para apresentar os conceitos básicos será usado um simples modelo composto apenas
por um elo e uma junta rotativa, ou seja, com apenas um grau de liberdade (GDL ou DOF –
Degree of Freedom). No modelo que é apresentado pela Figura 1 nota-se que o braço, de
comprimento R, gira em torno da origem do sistema de coordenadas do plano XY. Os cálculos
que serão apresentados posteriormente irão considerar R=1.
Y
R
(x,y)
θ
X
Figura 1 – Modelo com 1 grau de liberdade rotativo.
O ponto cuja trajetória será controlada é a extremidade livre que, dependendo do ângulo
θ, alcança diferentes coordenadas (x, y). Os cálculos da cinemática direta e inversa estão
apresentados no Quadro 1. Deve-se lembrar que neste caso as coordenadas que podem ser
atingidas estão restritas a uma circunferência.
2
Cinemática Direta
Cinemática Inversa
x = R ⋅ Cos(θ)
x
θ = ACos 
R
y = R ⋅ Sen(θ)
Quadro 1 – Equação da cinemática direta e inversa.
O cálculo da cinemática inversa pode ser realizado por outros meios, sendo mais
recomendado o uso da função ATan2. Como esta função não é disponibilizada em todas as
linguagens optou-se pelo uso da função ACos.
INTERPOLAÇÃO LINEAR
A forma mais simples de se mover uma junta rotativa da posição inicial θi até a posição
final θf em um tempo td é usando uma interpolação linear, ou seja, usando uma velocidade
angular constante. O Quadro 2 apresenta as equações de posição, velocidade angular e
aceleração angular para este caso.
Posição
 θ − θi
θ(t ) = θi +  f
 td

.t

Velocidade
Aceleração
θ − θi
θ& (t ) = f
td
&θ&(t ) = 0
Quadro 2 – Equações angulares para interpolação linear.
O símbolo θ& significa “derivada de θ”. Como θ é a posição angular do braço, sua
derivada fornece a velocidade angular. O símbolo &θ& significa “derivada de θ& ”, e como se trata
da derivada da velocidade angular obtém-se a aceleração angular. Apesar das três equações
serem funções relativas ao tempo, apenas a posição irá variar. Como se trata de um
deslocamento angular linear a velocidade é constante e a aceleração é nula.
Neste momento é interessante o uso de um exemplo numérico para fixação dos
conceitos. Suponha que a posição inicial do braço seja θ i = 0 o e que deseja-se atingir a posição
final θ f = 90 o em um intervalo de tempo t d = 10 segundos. Substituindo estes valores nas
equações do Quadro 2 obtém-se: θ(t ) = 9.t [graus] e θ& (t ) = 9 [graus/seg] . Variando t de 0 até 10
segundos podemos obter os gráficos da Figura 2.
3
Posição [graus]
100
Y
80
60
40
20
0
Tempo [seg]
0
1
2
3
4
5
6
7
8
9
10
Velocidade [graus/seg]
10
X
8
6
4
2
0
Tempo [seg]
0
1
2
3
4
5
6
7
8
9
10
Figura 2 – Gráficos de posição e velocidade para interpolação linear.
Não se deve esquecer que, apesar do gráfico de posição angular mostrar uma linha reta,
no espaço cartesiano o braço executa um arco de circunferência. O esquema do lado direito da
Figura 2 mostra a posição a cada segundo. Como a velocidade angular é constante tem-se
que a distância entre as posições é uniformemente distribuída.
Note que, em termos práticos, a aceleração é considerada nula. Porém é necessário um
pico de aceleração para iniciar o movimento e, no final, um pico de desaceleração para
interrompê-lo. Isso faz com que ocorram choques mecânicos muito fortes no início e no final da
trajetória, tornando esta forma de controle pouco adequada.
Os dados fornecidos para o exemplo estavam em graus, mas normalmente são
fornecidas coordenadas cartesianas para o destino e isso requer o cálculo da cinemática
inversa. Além disso, também é necessário verificar se a coordenada fornecida pode realmente
ser atingida. O Quadro 3 apresenta uma sugestão de algoritmo para o cálculo das grandezas
do Quadro 2 no tempo e também desenhar do braço. Os dados necessários são a coordenada
cartesiana de destino e o tempo de deslocamento. O algoritmo verifica se o ponto pode ser
atingido e em seguida faz o cálculo da cinemática inversa para determinar a posição angular
final da junta. Uma variável que contará a passagem do tempo é iniciada antes de um looping.
4
Dentro desse looping o tempo é incrementado para permitir o cálculo das variáveis
angulares (posição, velocidade e aceleração). Com base no valor da posição angular em cada
instante é possível desenhar a posição do braço usando os cálculos de cinemática direta.
Velocidade e aceleração não têm necessidade de ficar dentro do looping nesta situação, pois
são constantes no tempo, porém, nos casos seguintes, estas grandezas irão ser variáveis e
sendo assim o algoritmo posiciona o cálculo no devido lugar para manter-se compatível.
Definir R e θi
Ler x, y e td
Se Raiz(x2+y2)<>R então
Mensagem “Coordenada fora da área de trabalho”
Fim
Fim Se
Calcular θf=Acos(x/R)
t=0
Enquanto t < td fazer
Incrementar t
Calcular Posição Angular: θ = θi + t.(θf-θi)/td
Calcular Velocidade Angular: θ& =(θf-θi)/td
Calcular Aceleração Angular: &θ& =0
Traçar Linha de [0, 0] até [R*Cos(θ), R*Sen(θ)]
Fim Enquanto
Quadro 3 – Algoritmo para cálculo e traçado do movimento.
POLINÔMIO CÚBICO
O uso de uma equação cúbica para representar a posição angular no tempo elimina os
choques da interpolação linear. Da mesma forma exposto no caso linear as equações de
velocidade e aceleração são obtidas por derivação. A velocidade angular é representada por
uma equação quadrática e a aceleração angular por uma equação linear. No Quadro 4 são
apresentadas as três equações.
3.(θ f − θi )
2.(θf − θi )
Posição
θ(t ) = θi +
Velocidade
6.(θ f − θi )
6.(θ f − θi ) 2
θ& (t ) =
.t −
.t
2
3
td
td
Aceleração
&θ&(t ) = 6.(θ f − θi ) − 12.(θ f − θi ) .t
2
3
td
td
td
2
.t 2 −
td
3
.t 3
Quadro 4 – Equações angulares para interpolação não linear.
5
O algoritmo do Quadro 3 pode ser atualizado bastando substituir as equações de
posição, velocidade e aceleração pelas apresentadas no Quadro 4
Usando os mesmos
valores do exemplo numérico anterior, que são θ i = 0 o , θ f = 90 o e t d = 10 seg obtém-se os
valores da Tabela 1 e os gráficos da Figura 3.
Tabela 1 – Valores obtidos com as equações do Quadro 4.
Tempo
0
1
2
3
4
5
6
7
8
9
10
Posição
0.00
2.52
9.36
19.44
31.68
45.00
58.32
70.56
80.64
87.48
90.00
Velocidade
0.00
4.86
8.64
11.34
12.96
13.50
12.96
11.34
8.64
4.86
0.00
Aceleração
5.40
4.32
3.24
2.16
1.08
0.00
-1.08
-2.16
-3.24
-4.32
-5.40
Figura 3 – Gráficos resultantes das equações do Quadro 4.
A aceleração inicia-se com 5.4º/s2, permitindo que a velocidade saia do zero e inicie o
movimento do braço. Com a passagem do tempo o valor da aceleração diminui enquanto a
velocidade aumenta (cada vez mais lentamente) e o braço se afasta da posição de origem.
Exatamente na metade do movimento (45º) a aceleração é nula e a velocidade atinge o seu
valor máximo (13.5º/s). A partir desse ponto a aceleração passa a ser negativa, isto é, torna-se
uma desaceleração e, conseqüentemente, a velocidade diminui gradativamente. Próximo ao
final do movimento a velocidade é cada vez menor e isso faz o braço chegar ao destino
suavemente.
6
A Figura 4 apresenta a posição do braço variando no tempo (de 0 até 10 segundos).
Nota-se que apesar dos intervalos de tempo serem constantes as distâncias angulares em
cada momento não são. O movimento é lento no início e também no final.
Figura 4 – Posição do braço a cada 0.25 segundo.
O gráfico da Figura 4 foi obtido com um programa didático disponível em
http://www.iem.efei.br/gorgulho/download/planejador.zip. O programa simula os movimentos de
um braço com dois graus de liberdade e apresenta os gráficos de posição, velocidade e
aceleração para cada junta.
INTERPOLAÇÃO LINEAR COM EXTREMIDADES PARABÓLICAS
Outra estratégia de movimentação é, de certa forma, a união dos conceitos anteriores.
Tem-se uma movimentação linear com início e final do movimento suave (quadrático). A
denominação em inglês é linear segments with parabolic blends - LSPB. A Figura 5 apresenta
a forma de variação da posição, velocidade e aceleração para uma movimentação deste tipo.
Nota-se que há três fases distintas.
Fase 1 – Início Parabólico: no início do movimento há uma aceleração constante que faz com
que a velocidade aumente linearmente. Esse comportamento faz com que a posição
se altere cada vez mais rapidamente.
Fase 2 – Velocidade Linear: nesta etapa a aceleração deixa de existir, fazendo com que a
velocidade seja constante. A velocidade constante, por sua vez, faz com que o
deslocamento passe a ser linear.
7
Fase 3 – Final parabólico: para finalizar o movimento é usada uma desaceleração de valor
constante. Essa desaceleração diminui a velocidade de forma linear e faz com que a
posição varie cada vez mais lentamente até atingir a sua meta.
Figura 5 – Variação das grandezas no movimento linear-parabólico.
O instante no qual ocorre a transição da entrada parabólica para o deslocamento linear
será denominado de TA (também chamado de blend time). A posição angular do braço nesse
instante será definida como θA. Da mesma forma, o instante de transição do deslocamento
linear para a finalização parabólica será denominado TB e a posição angular de θB.
Como pode ser notado no gráfico o equacionamento que será apresentado a seguir
assume que os segmentos parabólicos têm a mesma duração, fazendo com que sejam
simétricos em relação ao ponto central. A duração dos segmentos parabólicos depende do
valor adotado para a aceleração e desaceleração. Quanto maior este valor menor é a porção
parabólica, fazendo com que o movimento tenda a uma interpolação linear simples. Do lado
oposto, quanto menor a aceleração, menor é a porção linear. Há um valor mínimo para a
aceleração, que faz com que a porção linear não exista, fazendo com que o gráfico da posição
seja similar à obtida pelo polinômio cúbico.
8
A Figura 6 mostra o mesmo movimento da Figura 5, mas com duas acelerações
angulares diferentes. Nos gráficos do lado esquerdo a aceleração angular adotada é igual à
aceleração angular mínima. Os gráficos do lado direito mostram a aceleração angular ajustada
para 100 vezes o valor da aceleração angular mínima.
Figura 6 – Esquerda: aceleração angular mínima. Direita: aceleração angular alta.
As várias equações necessárias para definir o movimento estão listadas no Quadro 5,
na ordem de cálculo. Os seguintes valores são necessários: ângulo inicial (θi), ângulo final (θf),
tempo de deslocamento (td) e fator de multiplicação da aceleração mínima (c) que deve ser
maior que 1. Na equação de TA usa-se subtração quando θf>θi e soma quando ocorrer o
contrário.
Aceleração Mínima
Aceleração Adotada
&θ& = 4.(θ − θ ) / t 2
min
f
i
d
&θ& = c.&θ&
min
(&θ&.t d )2 − 4.&θ&.(θf − θi ) / (2.&θ&)
Tempo A
TA = (t d / 2) ±
Ângulo A
θ A = θi + &θ&.TA 2 / 2
Tempo B
TB = t d − TA
Ângulo B
θ B = θ f − &θ&.TB 2 / 2
Velocidade Linear
(
(
)
)
θ& L = (θ B − θ A ) / (TB − TA )
Quadro 5 – Equações angulares para movimento linear com extremidades parabólicas.
9
Os valores angulares de posição, velocidade e aceleração em função do tempo são
calculados por equações diferentes conforme a fase em que se encontra o movimento. O
Quadro 6 apresenta estas equações.
Fase
Posição
(
Velocidade
Aceleração
)
1 ( t ≤ TA )
θ i + &θ&. t 2 / 2
&θ&.t
&θ&
2 ( TA < t < TB )
θi + θ& L .(t − TA )
θ& L
0
TB + θ& L .(t − TB ) − &θ&.( t − TB ) 2 / 2
θ& L − &θ&.(t − TB )
− &θ&
3 ( t ≥ TB )
Quadro 6 – Equações angulares para posição, velocidade e aceleração.
Juntamente com o programa didático há uma planilha do Excell (Linear-Parabólico.xls)
que implementa estes cálculos e apresenta os gráficos angulares de posição, velocidade e
aceleração.
TRAJETÓRIA DE TEMPO MÍNIMO
Em alguns sistemas robóticos os comandos de movimentação não incluem o tempo de
deslocamento, ou seja, o programador informa apenas a coordenada de destino. Nesses casos
o sistema irá atingir a meta no menor tempo possível. E para isso a aceleração angular
máxima permitida pelo equipamento é pré-programada pelo fabricante usando a interpolação
linear com extremidades parabólicas.
A forma de movimento nesta situação é mostrada do lado esquerdo da Figura 6, ou seja,
a aceleração angular máxima admissível é aplicada durante a primeira metade do movimento e
depois a desaceleração máxima é aplicada na segunda metade. O Quadro 7 apresenta as
equações que permitem calcular o tempo de deslocamento em função da aceleração angular e
a velocidade angular máxima atingida. Obviamente o momento de inversão da aceleração é
dado por td/2.
Tempo de Deslocamento
td =
4.(θ f − θi )
&θ&
max
2.(θ f − θ i )
θ& máx =
td
Velocidade Máxima
Quadro 7 – Equações para a trajetória de tempo mínimo.
10
MODELO COM DOIS GRAUS DE LIBERDADE
O modelo usado no artigo anterior, com apenas 1 grau de liberdade rotativo, possuía
uma área de trabalho muito limitada, resumida a uma circunferência. O modelo que será usado
deste momento em diante é composto por dois elos de mesmo tamanho e com eixos de
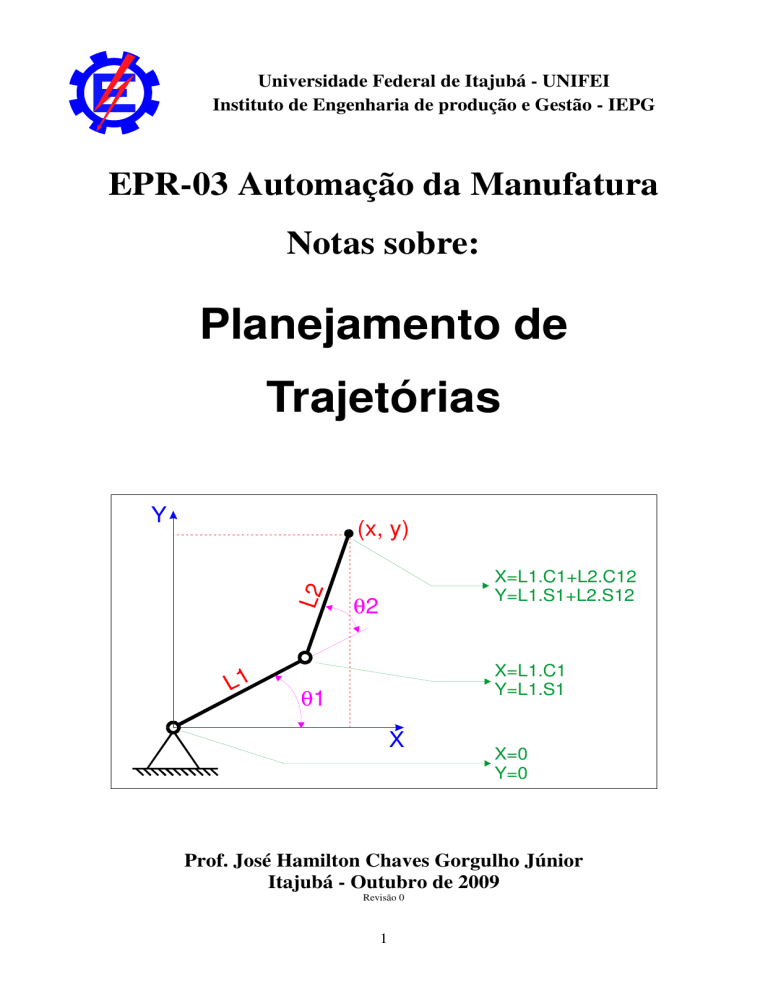
rotação paralelos. A Figura 7 apresenta o modelo cuja configuração faz com que a área de
trabalho seja um círculo com raio=1 (L1=L2=0.5).
Y
L2
(x, y)
L1
X=L1.C1+L2.C12
Y=L1.S1+L2.S12
θ2
X=L1.C1
Y=L1.S1
θ1
X
X=0
Y=0
Figura 7 – Modelo com dois graus de liberdade.
A Figura 7 traz também as coordenadas cartesianas das extremidades dos elos, obtidas
por cinemática direta (são úteis para desenhar o braço em um programa). Nessas equações
tem-se:
C1=Cos(θ1)
C12=Cos(θ1).Cos(θ2)-Sen(θ1).Sen(θ2)= Cos(θ1+θ2)
S1=Sen(θ1)
S12=Sen(θ1).Cos(θ2)+Cos(θ1).Sen(θ2)= Sen(θ1+θ2)
A cinemática inversa torna-se mais complexa do que o apresentado no artigo anterior. A
Figura 8 mostra que os dois elos formam um triângulo do qual será possível extrair, por uma
solução analítica, os valores de θ1 e θ2 quando forem fornecidas as coordenadas (x, y) da
extremidade.
Da análise da Figura 8 podem ser obtidas as seguintes relações:
R = X2 + Y2
X
Ar = ACos 
R
θ1 = Ar − A1
θ 2 = 180 − A 2
O valor de R é importante pois permite definir se a coordenada fornecida pode ser
atingida, ou seja, se R > L1 + L 2 então o ponto está fora da área de trabalho. Nota-se que Ar
não terá solução quando R=0 (como L1=L2 esta situação poderá ocorrer). Neste caso é
interessante definir θ2=180º e manter o valor atual de θ1 (que pode assumir qualquer valor).
11
Y
(X, Y)
A3
R2= X2+Y 2
R
θ2
L2
A2
A1
AR
θ1
L1
X
Figura 8 – Triângulo formado pelos dois elos.
Da trigonometria sabe-se que:
L2 2 = R 2 + L12 − 2.R.L1.Cos(A1)
e
R 2 = L12 + L2 2 − 2.L1.L2.Cos(A 2)
E obtém-se:
 R 2 + L12 − L2 2
A1 = ArcCos

2.R.L1





e
 L12 + L2 2 − R 2
A 2 = ArcCos

2.L1.L2





Pode-se agora elaborar um algoritmo para a cinemática inversa deste problema, como o
mostrado pelo Quadro 8.
Definir L1 e L2
Ler x e y
Calcular R=Raiz(x2+y2)
Se R>(L1+L2) então “Coordenada não pode ser atingida”
Se R=0 então
Definir θ2=180
Senão
Calcular Ar=ArcCos(x/R)
Calcular A1=ArcCos((R2+L12-L22)/(2.R.L1))
Calcular A2=ArcCos((L12+L22-R2)/(2.L1.L2))
Calcular θ1=Ar-A1
Calcular θ2=180-A2
Fim-Se
Quadro 8 – Algoritmo para a Cinemática Inversa.
12
O Quadro 9 apresenta um algoritmo para o cálculo e desenho do braço com dois graus
de liberdade. Os cálculos de posição angular, velocidade angular e aceleração angular são
exatamente iguais aos apresentados no primeiro artigo e, agora, são calculados para cada elo.
Definir L1, L2, θi1, θi2
Ler x, y e td
Cinemática Inversa (calcular θf1, θf2)
t=0
Enquanto t<td fazer
Incrementar t
Calcular Posição (θ1 e θ2)
Calcular velocidade (θ1 e θ2)
Calcular Aceleração (θ1 e θ2)
C1=Cos(θ1)
S1=Sin(θ1)
C12= Cos(θ1+θ2)
S12= Sen(θ1+θ2)
Traçar Linha de [0, 0] até [L1.C1, L1.S1]
Traçar Linha de [L1.C1, L1.S1] até [L1.C1+L2.C12, L1.S1+L2.S12]
Fim Enquanto
Quadro 9 – Algoritmo para planejamento de trajetória.
As próximas três figuras mostram a movimentação do braço usando as três abordagens
matemáticas apresentadas. A coordenada de origem é (1, 0) e a de destino é (-0.25, 0.75),
com tempo de deslocamento de 5 segundos. Para cada movimentação são mostrados os
gráficos de θ1 (os gráficos de θ2 possuem forma similar). A posição do braço foi desenhada a
cada décimo de segundo aproximadamente. Na Figura 9 está o resultado da interpolação
linear, onde nota-se o espaçamento eqüidistante dos pontos no trajeto.
13
Figura 9 – Interpolação linear.
Na Figura 10 foi usado o polinômio cúbico. A densidade de pontos é maior no início e
vai sendo reduzida até atingir a metade do percurso. A partir deste ponto vai aumentando
novamente até atingir o ponto meta.
Figura 10 – Polinômio cúbico.
A Figura 11 mostra a interpolação linear com extremidades parabólicas. Foi usado um
fator c=1.25, ou seja, a aceleração adotada é 1.25 vezes a aceleração mínima. A densidade
dos pontos é variável no início e final enquanto na porção central o espaçamento é igual.
14
Figura 11 – Interpolação linear com extremidades parabólicas.
TRAJETÓRIA COM PONTOS INTERMEDIÁRIOS
A Tabela 2 apresenta um conjunto de pontos que serão percorridos para comparar as
três estratégias apresentadas.
Tabela 2 – Valores para x, y e tempo de múltiplos pontos.
Ponto
Coordenada
X [m]
Coordenada
Y [m]
Tempo de
Deslocamento [s]
Origem
1.0
0.0
-
1
0.65
0.65
3.0
2
0.0
0.25
3.0
3
-0.65
0.65
3.0
4
0.0
-0.75
3.0
5
0.35
0.35
3.0
A Figura 12 apresenta a movimentação pelos pontos mostrados pela Tabela 2 usando a
interpolação linear, bem como os gráficos de θ1. Os pontos programados estão marcados por
um x de cor branca. Nota-se que o espaçamento entre os pontos é igual em cada trecho. Como
o tempo é igual para cada deslocamento tem-se que, onde a distância é menor, a velocidade é
mais alta. O gráfico de velocidade angular mostra que esta grandeza varia bruscamente. Pelos
gráficos é possível concluir que o segundo movimento ocorre no sentido contrário dos demais
(posição diminui e a velocidade é negativa).
15
Figura 12 – Múltiplos pontos usando interpolação linear.
A movimentação usando o polinômio cúbico está na Figura 13. A posição angular alterase suavemente. Fica claro também que a velocidade angular é nula no início e final de cada
trecho do percurso.
Figura 13 – Múltiplos pontos usando polinômio cúbico.
A Figura 14 exibe a movimentação usando a interpolação linear com extremidades
parabólicas (fator c=1.25). Nesta situação a velocidade angular também é nula no início e final
de cada trecho do percurso, ou seja, no ponto programado a velocidade angular é zero para os
dois elos.
16
Figura 14 – Múltiplos pontos usando interpolação linear com extremidades parabólicas.
Na Figura 15 são mostrados os gráficos de θ2 para as três situações. As formas dos
gráficos de posição e velocidade angular apresentam uma similaridade bastante alta.
Comparando estes gráficos com os gráficos de θ1 é possível perceber que cada elo executa
um movimento diferente, que requer variação de velocidade e aceleração diferentes também.
Figura 15 – Múltiplos pontos usando interpolação linear com extremidades parabólicas.
DEFININDO A VELOCIDADE NO PONTO
A interpolação linear com extremidades parabólicas permite, por meio de cálculos
adicionais, definir a velocidade angular das juntas nos pontos intermediários de uma trajetória,
mas devido a sua complexidade esta técnica não será abordada. Já, para o polinômio cúbico, o
17
equacionamento é mais simples e está exibido no Quadro 10. Foram usados quatro
parâmetros (a0 até a3) para simplificar a visualização.
a 0 = θi
θ(t ) = a 0 + a 1 .t + a 2 .t 2 + a 3 .t 3
a 1 = θ& i
3
2 & θ& f
(
)
θ
−
θ
−
θi −
f
i
td
td
t d2
θ& (t ) = a 1 + 2.a 2 .t + 3.a 3 .t 2
a2 =
&θ&(t ) = 2.a + 6.a .t
2
3
a3 = −
2
(θf − θi ) + 12 θ& f + θ& i
3
td
td
(
)
Quadro 10 – Equações para polinômio cúbico com velocidade no ponto.
Analisando os parâmetros nota-se que além da posição inicial (θi), posição final (θf) e
tempo de deslocamento (td) devem ser fornecidas as velocidades angulares inicial ( θ& i ) e final
( θ& f ). Se as velocidades angulares inicial e final forem nulas obtém-se o polinômio cúbico
apresentado anteriormente.
Deve ficar claro que o primeiro movimento de um caminho de múltiplos pontos tem
velocidade inicial nula e que o último movimento tem velocidade final nula. Nos demais a
velocidade final de um trecho é igual a velocidade inicial do trecho seguinte.
As equações apresentadas são para apenas uma junta. Para sistemas com mais juntas
é possível definir a velocidade angular de cada uma delas separadamente. Esta definição de
velocidades pode ser feita de vários modos. Pode-se optar, por exemplo, pela determinação
automática usando alguma heurística que mantenha uma aceleração constante nos pontos
intermediários. Outra forma depende da escolha de velocidades cartesianas no ponto (Vx e Vy)
que irão refletir em velocidades angulares nas juntas.
A Figura 16 mostra o resultado da movimentação pelos pontos da Tabela 2 com a
velocidade das duas juntas configuradas para 20º/s. No plano XY a trajetória toma uma forma
diferente da observada na Figura 13 para possibilitar que a velocidade angular programada
seja atingida. Do lado direito, no gráfico de velocidade, observa-se que ao final de cada
movimento a velocidade angular atingiu o valor de 20º/s.
18
Figura 16 – Polinômio cúbico com velocidade de 20º/s nos pontos intermediários.
Usar valores muito elevados faz com que os movimentos sofram “deformações” para
possibilitar que sejam atingidas as velocidades angulares programadas. Na Figura 17 foi
usado 60º/s para as duas juntas, em todos os pontos intermediários. Durante a execução é
interessante observar o movimento entre a origem e o primeiro ponto. O braço move-se
inicialmente em sentido contrário para ter espaço suficiente para acelerar e atingir a velocidade
angular definida.
Figura 17 - Polinômio cúbico com velocidade de 60º/s nos pontos intermediários.
19
O ESPAÇO CARTESIANO
A Figura 18 mostra um movimento em linha reta (straight line motion) entre os pontos I
(início) e F (fim). O movimento foi dividido em 5 partes, ou seja, há quatro pontos intermediários
entre I e F. Conhecendo-se as coordenadas cartesianas de cada um destes pontos é possível
calcular, por cinemática inversa, os valores de θ1 e θ2 necessários.
Y
F
∆X
∆Y
I
X
Figura 18 – Movimento em linha reta no espaço cartesiano.
A Figura 18 também mostra que a divisão da trajetória cria intervalos de igual dimensão
para cada eixo, que foram denominados de ∆X e ∆Y. Quanto menor a dimensão destes
intervalos mais linear será a trajetória.
O Quadro 11 mostra um algoritmo para executar os cálculos de uma trajetória no
espaço cartesiano. Nota-se que a cinemática inversa passa a figurar dentro do looping de
tempo.
Definir L1, L2, θi1, θi2
Ler x, y e td
t=0
Enquanto t<td fazer
Incrementar t
Cálculos Cartesianos do Elo 2 (X2, Y2, Vx2, Vy2, Ax2 e Ay2)
Cinemática Inversa
Cálculos Trigonométricos
Cálculos Angulares
Cálculos Cartesianos do Elo 1
Fim Enquanto
Quadro 11 – Algoritmo para planejamento de trajetória no espaço cartesiano.
20
Os cálculos cartesianos do Elo 2 definem a posição, velocidade e aceleração do órgão
terminal a cada instante do movimento e em cada eixo. Na literatura é comum encontrar outra
& 2 para velocidade do elo 2 no eixo X e X
&& 2 para
notação para os símbolos, como por exemplo, X
aceleração. As equações desses cálculos dependem da estratégia de movimento adotada e
serão abordadas adiante.
A cinemática inversa, apresentada nos artigos anteriores, é responsável por calcular os
valores de θ1 e θ2 para cada coordenada (X2, Y2) do movimento, ou seja, a cada instante
calcula-se os ângulos necessários para que a posição desejada seja atingida. O Quadro 12
apresenta duas equações que podem ser usadas neste cálculo (note o uso de uma outra
notação para a função arco-tangente de dois argumentos). Como θ1 depende de Sin(θ2) e
Cos(θ2) é óbvio que é necessário calcular inicialmente θ2 (que depende de X2, ,Y2, L1 e L2).
 L2.Sin (θ2) 
 Y2 

θ1 = ArcTan 2
 − ArcTan 2
 X2 
 L1 + L2.Cos(θ2) 
 X 2 2 + Y 2 2 − L12 − L2 2 

θ2 = ArcCos

2
.
L
1
.
L
2


Quadro 12 – Cinemática inversa.
Após a cinemática inversa obter θ1 e θ2 pode-se calcular o valor instantâneo das
funções trigonométricas que serão necessárias na próxima etapa. O Quadro 13 mostra estas
funções.
C1=Cos(θ1)
S1=Sin(θ1)
C2=Cos(θ2)
S2=Sin(θ2)
C12= Cos(θ1+θ2)
S12= Sen(θ1+θ2)
Quadro 13 – Cálculos trigonométricos.
Uma possibilidade é unir as duas etapas anteriores na seguinte seqüência de cálculos:
θ2, C2, S2, θ1, C1, S1, C12 e S12. A etapa seguinte consiste em calcular as grandezas
angulares faltantes dos dois elos, que são velocidade e aceleração. O Quadro 14 mostra as
equações para os cálculos para o exemplo de dois graus de liberdade. Para facilitar a leitura o
símbolo θ& usado para representar a velocidade angular foi substituído por Va e o símbolo &θ&
para representar a aceleração angular foi substituído por Aa.
21
Va1 =
(Vx 2.C12 + Vy2.S12)
L1.S2
Va 2 =
(−L1.C1 − L2.C12).Vx 2 − (L1.S1 + L2.S12).Vy 2
L1.L2.S2
Aa1 =
(Va1 + Va 2).(C12.Vy 2 − S12.Vx 2) + C12.Ax 2 + S12.Ay2 − L1.C2.Va1.Va 2
L1.S2
Aa 2 =
− (X 2.Ax 2 + Y 2.Ay2 + Vx 2 2 + Vy2 2 + L1.L2.C2.Va 2 2 )
L1.L2.S2
Quadro 14 – Cálculos das velocidades angulares e das acelerações angulares.
A última etapa envolve o cálculo das grandezas cartesianas do Elo 1, que são posição,
velocidade e aceleração para cada eixo. O Quadro 15 apresenta as equações necessárias.
X1 = L1.C1
Y1 = L1.S1
Vx1 = −L1.S1.Va1
Vy1 = L1.C1.Va1
Ax1 = − L1.(C1.Va12 + S1.Aa1)
Ay1 = − L1.(S1.Va12 − C1.Aa1)
Quadro 15 – Cálculos cartesianos do Elo 1.
Deve ficar claro que, se o objetivo é apenas enviar dados de posição para um robô ou
plotar uma imagem em uma tela, vários cálculos não são necessários. Tendo o valor de θ1 e θ2
a cada instante as velocidades e acelerações, tanto angulares quanto cartesianas, são
conseqüências físicas do movimento.
PROBLEMAS GEOMÉTRICOS NAS COORDENADAS CARTESIANAS
O primeiro problema geométrico que pode ocorrer quando o planejamento de trajetória é
realizado no espaço cartesiano está ligado à forma do espaço de trabalho. Dependendo da
dimensão dos elos e dos limites de movimento a região de trabalho possuirá convexidades e,
dessa forma, um movimento em linha reta poderá passar por pontos fora da área de trabalho.
A Figura 19 mostra o espaço de trabalho típico de um robô SCARA com um exemplo de uma
trajetória em linha reta que não pode ser realizada.
No modelo usado como exemplo tem-se L1=L2 e nenhuma restrição quanto aos ângulos
máximos. Isso faz com que a área de trabalho não possua nenhuma convexidade. Dessa
forma é possível obter qualquer trajetória retilínea entre coordenadas válidas.
22
Y
X
Figura 19 – Problema no movimento cartesiano retilíneo.
Um outro problema geométrico está ligado às singularidades. Quando o braço
aproxima-se de uma configuração singular uma ou mais juntas terão suas velocidades
aumentadas muito rapidamente. Na posição singular essas velocidades tendem ao infinito. Isso
pode ser matematicamente verificado observando-se as equações do Quadro 3. Nas quatro
equações o divisor possui S2 que atinge o valor zero quando θ2 vale 0º ou 180º. Nessas
posições os valores de Va1, Va2, Aa1 e Aa2 são levados ao infinito e, por conseqüência,
também os valores de Vx1, Vy1, Ax1 e Ay1. A Figura 20 mostra um exemplo típico da
execução de um movimento linear que passa próximo de uma configuração singular.
Figura 20 – Movimento passando próximo de uma configuração singular.
O movimento executado na Figura 20 vai de (0.8, 0.05) para (-0.8, 0.05). O movimento
inicia-se com θ1 girando no sentido negativo (tendendo a atingir -90º) e θ2 girando no sentido
positivo (tendendo atingir 180º). Conforme se aproxima da coordenada (0, 0) é necessário que
θ1 gire rapidamente no sentido positivo para permitir a continuidade do movimento. Quanto
23
menor o valor de Y para esse movimento, mais rapidamente esse giro em torno da origem vai
ocorrer. Se o movimento passar pela origem o movimento seria instantâneo, ou seja, em um
instante tem-se θ1=-90º e no instante seguinte tem-se θ1=90º, como mostra a Figura 21.
Figura 21 – Movimento passando em uma configuração singular.
INTERPOLAÇÃO LINEAR
Da mesma forma como mostrado no primeiro artigo, a estratégia mais simples de
movimentação é por meio de uma interpolação linear. Basicamente as equações são idênticas
às mostradas para a movimentação linear no espaço angular. A diferença é que as variáveis
não são mais angulares e sim cartesianas. O Quadro 16 mostra as equações cartesianas para
interpolação linear, tanto para o eixo X quanto para o eixo Y. Nota-se que a velocidade em
cada eixo é constante e a aceleração é nula.
Posição
Velocidade
X 2(t ) = X 2 i +
(X 2 f − X2i ) .t
Vx 2 =
(X 2 f − X 2i )
Y 2(t ) = Y 2 i +
(Y 2 f − Y2i ) .t
Vy 2 =
(Y2 f − Y2i )
td
td
td
Aceleração
Ax 2(t ) = 0
Ay2(t ) = 0
td
Quadro 16 – Equações cartesianas para interpolação linear.
A Figura 22 mostra o resultado da movimentação do braço usando as equações do
Quadro 16, bem como os gráficos de posição, velocidade e aceleração para o eixo Y. Os
dados são os mesmos usados no artigo anterior, ou seja, origem em (1, 0), destino (-0.25, 0.75)
e tempo de deslocamento de 5 segundos. Nota-se o espaçamento igual entre os pontos
durante todo o movimento, confirmando que o movimento é linear no tempo (e no espaço).
24
Figura 22 – Movimento com interpolação linear no espaço cartesiano.
Na Figura 23 são mostrados os gráficos de posição para os ângulos θ1 e θ2. Nota-se
que enquanto os movimentos do elo 2 em X e Y são lineares, os movimentos angulares de θ1
e θ2 possuem outras formas.
Figura 23 – Gráficos de Teta1 e Teta2.
POLINÔMIO CÚBICO
A uso de um polinômio cúbico é uma das formas de se evitar os choques mecânicos no
início e fim dos movimentos. No Quadro 17 estão as equações cartesianas que permitem que
o movimento em linha reta seja executado de maneira mais suave. Apenas as equações do
eixo X estão representadas. Para obter as equações de Y basta substituir o nome das variáveis.
Posição
X 2(t ) = X 2i +
Velocidade
Vx 2(t ) =
Aceleração
Ax(t ) =
3
(X 2f − X2i ).t 2 − 23 (X2f − X 2i ).t 3
2
td
td
6
(X2f − X 2i ).t − 63 (X 2f − X2i ).t 2
2
td
td
6
(X 2f − X 2i ) − 123 (X2f − X 2i ).t
2
td
td
Quadro 17 – Polinômio cúbico cartesiano (para o eixo X).
25
A Figura 24 mostra, no lado esquerdo, o movimento entre (1, 0) e (-0.25, 0.75) em 5
segundos usando o polinômio cúbico. O espaçamento entre os pontos é maior na posição
central, quando a velocidade é maior, enquanto que nas extremidades o espaçamento diminui.
No lado direito estão os gráficos de posição, velocidade e aceleração em Y (em X a forma é
similar).
Figura 24 – Movimento com polinômio cúbico no espaço cartesiano.
INTERPOLAÇÃO LINEAR COM EXTREMIDADES PARABÓLICAS
Esta abordagem matemática também elimina os choques mecânicos do início e fim do
movimento cartesiano linear. O equacionamento é similar ao que foi apresentado no artigo
inicial, bastando substituir as variáveis angulares por suas correspondentes variáveis
cartesianas. Na Figura 25, à esquerda, está o movimento no espaço cartesiano, enquanto do
lado direito estão os gráficos de posição, velocidade e aceleração em Y (em X a forma é
similar).
26
Figura 25 – Interpolação linear com extremidades parabólicas no espaço cartesiano.
O conceito de trajetória de tempo mínimo, abordado na primeira parte, também pode ser
aplicado no espaço cartesiano, porém não é usual. Se o objetivo é realizar movimentos rápidos
então o espaço das juntas é muito superior ao espaço cartesiano (para esta configuração de
juntas rotativas).
TRAJETÓRIA COM PONTOS INTERMEDIÁRIOS
Da mesma maneira como ocorreu no espaço das juntas, no espaço cartesiano também
pode-se realizar movimentos em linha reta com pontos intermediários. Na Figura 26 estão os
resultados obtidos com interpolação linear (normal e com extremidades parabólicas).
Figura 26 – Interpolação linear (esquerda) e interpolação linear com extremidades parabólicas (direita).
O polinômio cúbico permite a definição da velocidade no ponto. Se as velocidades em X
e Y são iguais a zero o movimento é realmente uma linha reta. Caso seja definida alguma
velocidade o trajeto cartesiano se deforma. Na Figura 27 à esquerda está o movimento com
27
velocidade nula em todos os pontos. No lado direito foi programada a mesma velocidade em
todos os pontos (-0.25 m/s em X e 0 em Y).
Figura 27 – Polinômio cúbico sem e com velocidade nos pontos.
Na Figura 28 estão os gráficos de posição, velocidade e aceleração em X e Y. Em X
pode-se ver que a velocidade é de -0.25 m/s no final de cada etapa, enquanto que em Y a
velocidade é nula.
Figura 28 – Gráficos de posição, velocidade e aceleração.
28
COMENTÁRIOS FINAIS
O objetivo deste texto foi introduzir os conceitos sobre o planejamento de trajetória, que
vai muito além do que foi exposto. O modelo explorado, com apenas dois graus de liberdade,
não necessitou de equações matriciais, mas é possível imaginar que o aumento dos graus de
liberdade faz com que a complexidade seja elevada. Além disso, a alteração dos tipos de junta
do robô também levam a grandes alterações matemáticas.
Outros fatores que envolvem o controle da posição do órgão terminal não foram
abordados, apesar da grande importância. Pode-se citar o torque e a inércia que influenciam
fortemente o controle PID que busca manter a trajetória real o mais próxima possível da
trajetória calculada.
REFERÊNCIAS
Craig, J. J., Introduction to Robotics – Mechanics & Control, Addison-Wesley Publishing
Company, 1955.
Fu, K. S.; Gonzáles, R. C.; Lee, C. S. G., Robotics: Control, Sensing, Vision, and
Intelligence, McGraw Hill Book Company, 1987.
Koren, Y., Robotics for Engineers, McGraw Hill Book Company, 1985.
Spong, M. W.; Vidyasagar, M.; Robot Dynamics and Control, John Wiley & Sons, Inc., 1989.
Paul, R. P., Robot Manipulators: Mathematics, Programming, and Control – The Computer
Control of Robot Manipulators, Massachusetts Institute of Technology (1981), Ninth
Printing, 1992.
29