Tópico 6 - engfisica

Tópico 6 – Trabalho e potência
229
4 Uma força de intensidade 20 N atua em uma partícula na mesma
direção e no mesmo sentido do seu movimento retilíneo, que acontece
sobre uma mesa horizontal. Calcule o trabalho da força, considerando
um deslocamento de 3,0 m.
Tópico 6
1 Na figura abaixo, embora puxe a carroça com uma força horizontal de 1,0 · 103 N, o burro não consegue tirá-la do lugar devido ao
entrave de uma pedra:
Resolução:
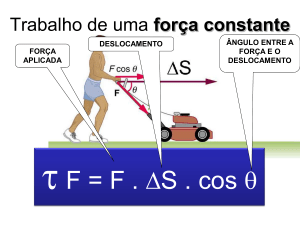
τ=Fdωsθ
No caso, θ = 0º e cos θ = 1
τ = F d ⇒ τ = 20 · 3,0 (J)
τ = 60 J
Resposta: 60 J
5
Qual o trabalho da força do burro sobre a carroça?
No esquema da figura, uma mesma caixa é arrastada três vezes
ao longo do plano horizontal, deslocando-se do ponto A até o ponto B:
Resolução:
O trabalho é nulo, já que a referida força não produz deslocamento.
F1
F2
Resposta: Trabalho nulo
F3
2
No SI, a unidade de trabalho pode ser expressa por:
a) kg · m2
d) kg · m
s
s
2
2
m
m
b) kg · 2
e) kg · 3
s
s
c) kg2 · m2
s
Resolução:
No SI, a unidade de trabalho é o joule (J).
J = N m = kg · m2 · m
s
Logo:
2
J = kg · m2
s
A
B
Na primeira vez, é puxada pela força F1 , que realiza um trabalho τ1; na
segunda, é puxada pela força F2 , que realiza um trabalho τ2; e na terceira é puxada por uma força F3 , que realiza um trabalho τ3. Supondo os
comprimentos dos vetores da figura proporcionais às intensidades de
F1 , F2 e F3 , aponte a alternativa correta.
a) τ1 > τ2 > τ3
b) τ1 < τ2 < τ3
c) τ1 = τ2 = τ3
d) τ1 = τ2 = 0
e) τ1 = τ2 < τ3
Resposta: b
3
E.R. Um homem empurra um carrinho ao longo de uma estra-
da plana, comunicando a ele uma força constante, paralela ao deslocamento, e de intensidade 3,0 · 102 N. Determine o trabalho realizado
pela força aplicada pelo homem sobre o carrinho, considerando um
deslocamento de 15 m.
Resolução:
A situação descrita está representada a seguir:
F
Picolés
Picolés
d
Sendo F e d de mesma direção e mesmo sentido, o trabalho de F
fica dado por:
τ(F ) = F d
Resposta: c
6 Considere um garoto de massa igual a 50 kg em uma roda-gigante que opera com velocidade angular constante de 0,50 rad/s.
Supondo que a distância entre o garoto e o eixo da roda-gigante seja
de 4,0 m, calcule:
a) a intensidade da força resultante no corpo do garoto;
b) o trabalho realizado por essa força ao longo de meia volta.
Resolução:
a) F = Fcp ⇒ F = m ω2 R
F = 50 (0,50)2 · 4,0 (N)
F = 50 N
b) O trabalho é nulo, pois a força resultante no corpo do garoto é centrípeta (perpendicular à trajetória).
Como F = 3,0 · 102 N e d = 15 m, vem:
τ(F ) = 3,0 · 102 · 15 (J ) ⇒
Resolução:
As três forças realizam trabalhos iguais, já que a projeção das três na
direção do deslocamento é a mesma.
τ(F ) = 4,5 · 103 J
Respostas: a) 50 N ; b) zero
230
PARTE II – DINÂMICA
7
A intensidade da resultante das forças que agem em uma partícula varia em função de sua posição sobre o eixo Ox, conforme o gráfico a seguir:
F (N)
20
0
2,0
4,0
6,0
8,0
10
12 x (m)
–20
a) Determine os coeficientes de atrito estático e cinético entre a caixa
e o solo.
b) Determine o trabalho realizado pelo carregador ao arrastar a caixa
por 5 m.
c) Qual seria o trabalho realizado pelo carregador se a força horizontal
aplicada inicialmente fosse de 20 N? Justifique sua resposta.
Resolução:
a) Fat = μe Fn = μe m g
d
30 = μe 20 · 10 ⇒ μd = 0,15
Fat = μe Fn = μe m g
c
–40
Calcule o trabalho da força para os deslocamentos:
a) de x1 = 0 a x2 = 8,0 m;
b) de x2 = 8,0 m a x3 = 12 m;
c) de x1 = 0 a x3 = 12 m.
Resolução:
(8,0 + 4,0) 20
= 120 J
a) τ = A1 =
2
x1 → x2
b) τ = A2 =
x2 → x3
c)
4,0 (–40)
= 80 J
2
b) = F d ⇒ = 20 · 5 (J) ⇒
Respostas: a) 0,15 e 0,10; b) 100 J; c) Trabalho nulo, pois a força não
provoca deslocamento na caixa.
10 E.R. Uma partícula percorre o eixo Ox indicado, deslocando-se
da posição x1 = 2 m para a posição x2 = 8 m:
F1
F2
2
0
τ = 120 – 80 = 40 J
x1 → x3
Respostas: a) 120 J ; b) – 80J; c) 40 J
8
(UCG-GO) Uma força constante F , horizontal, de intensidade
20 N, atua durante 8,0 s sobre um corpo de massa 4,0 kg que estava
em repouso apoiado em uma superfície horizontal perfeitamente sem
atrito. Não se considera o efeito do ar. Qual o trabalho realizado pela
força F no citado intervalo de tempo?
Resolução:
(I) F = m a ⇒ 20 = 4,0 a
a = 5,0 m/s2
(II) MUV: d = v0 t + a t2
2
d = 5,0 (8,0)2 (m) ⇒ d = 160 m
2
(III) τ = F d cos θ
(θ = 0 ° e cos θ = 1)
τ = F d ⇒ τ = 20 · 160 (J)
τ = 3,2 · 103 J
Resposta: 3,2 · 103 J
(Fuvest-SP) Um carregador em um depósito empurra, sobre o
solo horizontal, uma caixa de massa 20 kg, que inicialmente estava em
repouso. Para colocar a caixa em movimento, é necessária uma força
horizontal de intensidade 30 N. Uma vez iniciado o deslizamento, são
necessários 20 N para manter a caixa movendo-se com velocidade
constante. Considere g = 10 m/s2.
= 100 J
c) Trabalho nulo, pois essa força (20 N) não venceria o atrito de destaque (30 N) e a caixa não sofreria nenhum deslocamento.
τ = τ + τ
x1 → x3 x1 → x2 x2 → x3
9
μc = 0,10
20 = μe 20 · 10 ⇒
60°
4
6
8
10
12
x (m)
Sobre ela, agem duas forças constantes, F1 e F2 , de intensidades respectivamente iguais a 80 N e 10 N. Calcule os trabalhos de
F1 e F2 no deslocamento de x1 a x2.
Resolução:
O trabalho de F1 é motor (positivo), sendo calculado por:
τ(F ) = F1 d cos θ1
1
Tendo-se F1 = 80 N, d = x2 – x1 = 8 m – 2 m = 6 m e θ1 = 60°, vem:
τ(F ) = 80 · 6 · cos (60°) (J) ⇒ τ(F ) = 240 J
1
1
O trabalho de F2 é resistente (negativo), sendo calculado por:
τ(F ) = F2 d cos θ2
2
Tendo-se F2 = 10 N, d = 6 m e θ2 = 180°, vem:
τ(F ) = 10 · 6 · cos (180°) (J) ⇒ τ(F ) = – 60 J
2
2
11 Na figura, o homem puxa a corda com uma força constante, horizontal e de intensidade 1,0 · 102 N, fazendo com que o bloco sofra,
com velocidade constante, um deslocamento de 10 m ao longo do
plano horizontal.
Tópico 6 – Trabalho e potência
Desprezando a influência do ar e considerando o fio e a polia ideais,
determine:
a) o trabalho realizado pela força que o homem exerce na corda;
b) o trabalho da força de atrito que o bloco recebe do plano horizontal
de apoio.
Resolução:
a) τ(F ) = F d cos α
(α = 0° e cos α = 1)
τF = 1,0 · 102 · 10 · (1) (J)
231
F1
F2
60°
T
A
Admitindo que a intensidade de F1 seja 10 N e que o anel sofra um
deslocamento de 2,0 m da esquerda para a direita, calcule:
a) a intensidade de F2 ;
b) os trabalhos de F1 e F2 no deslocamento referido.
τF = 1,0 · 103 J
b) MRU: Fat = F
τF = Fat d cos β
Resolução:
a) F1 = F1 cos 60° ⇒ F1 = 10 · 1 (N)
X
X
2
at
(β = 180° e cos β = –1)
τF = 1,0 · 102 · 10 (–1) (J)
F1 = 5,0 N
X
at
τF = – 1,0 · 103 J
Cada quadradinho da figura tem lado equivalente a 1,0 N.
F2 = –3,0 x + 4,0 y ⇒ F22 = (3,0)2 + (4,0)2
at
Respostas: a) 1,0 · 103 J; b) – 1,0 · 103 J
F2 = 5,0 N
12 O bloco da f igura acha-se inicialmente em repouso, livre da
ação de forças externas. Em dado instante, aplica-se sobre ele o sistema de forças indicado, constituído por F1 , F2 , F3 e F4 , de modo que
F1 e F3 sejam perpendiculares a F4 :
X
1
1
τF = 10 J
1
τF = F2 d cos 180° ⇒ τF = 3,0 · 2,0 · (–1) (J)
X
2
2
τF = –6,0 J
F3 = 120 N
2
θ
F4 = 50 N
b) τ = F d cos 0° ⇒ τ = 5,0 · 2,0 (J) ⇒
1
F
F
F2 = 100 N
sen θ = 0,80
cos θ = 0,60
F1 = 200 N
Respostas: a) 5,0 N; b) 10 J e –6,0 J
14 O esquema a seguir ilustra um homem que, puxando a corda
verticalmente para baixo com força constante, arrasta a caixa de peso
4,0 · 102 N em movimento uniforme, ao longo do plano inclinado:
o
od
tid ento
n
Se vim
mo
Sendo τ1, τ2, τ3 e τ4, respectivamente, os trabalhos de F1 , F2 , F3 e F4 para
um deslocamento de 5,0 m, calcule τ1, τ2, τ3 e τ4.
Resolução:
O bloco se deslocará para a direita, já que F2 = F2 · cos θ supera
X
F4 (60 N 50 N).
Forças perpendiculares ao deslocamento não realizam trabalho, logo:
τ1 = τ3 = 0
τ2 = F2 d cos θ = 100 · 5,0 · 0,60 (J)
τ2 = 300 J
τ4 = F4 d cos α = 50 · 5,0 (–1) (J)
τ4 = –250 J
Resposta: 1 = 0, 2 = 300 J, 3 = 0 e 4 = –250 J
13 Na figura, estão representadas em escala duas forças F e F
1
2
aplicadas em um anel que pode se movimentar ao longo de um trilho
horizontal T.
30°
Desprezando os atritos e a influência do ar e admitindo que a corda e a
roldana sejam ideais, calcule o trabalho da força exercida pelo homem
ao provocar na caixa um deslocamento de 3,0 m na direção do plano
inclinado.
Resolução:
(I) MRU: F = Pt
F = P sen 30° ⇒ F = 4,0 · 102 · 1 (N)
2
F = 2,0 · 102 N
(II) τF = F d cos 0° ⇒ τF = 2,0 · 102 · 3,0 (J)
τF = 6,0 · 102 J
Resposta: 6,0 · 102 J
232
PARTE II – DINÂMICA
15 O gráfico abaixo representa a variação do valor algébrico das
Resolução:
duas únicas forças que agem em um corpo que se desloca sobre um
eixo Ox. As forças referidas têm a mesma direção do eixo.
θ
L
F (N)
80
(F1)
60
θ
T
40
Ty
20
5
10
15
0
Tx
x (m)
(F2)
–20
P
Calcule:
a) o trabalho da força F1, enquanto o corpo é arrastado nos primeiros
10 m;
b) o trabalho da força F2, enquanto o corpo é arrastado nos primeiros
10 m;
c) o trabalho da força resultante, para arrastar o corpo nos primeiros
15 m.
sen θ = R
L
sen θ = 30 ⇒
50
sen θ = 0,6
sen2 θ + cos2 θ = 1
(0,6)2 + cos2 θ = 1 ⇒
cos θ = 0,8
a) Equilíbrio na vertical:
TY = P ⇒ T cos θ = m · g
Resolução:
a) τ = (60 + 20) 10 ⇒ τF = 4,0 · 102 J
F1
1
2
T 0,8 = 2,4 · 10 ⇒
T = 30 N
b) MCU na horizontal: Fcp = Tx
m ω2 R = T sen θ ⇒ 2,4 ω2 0,30 = 30 · 0,6
b) τ = 10 (–20) ⇒ τF = –1,0 · 102 J
F2
2
2
c) τ =
O
R
(80 + 20) 15 10 (–20) 5 (–20)
+
+
⇒
2
2
2
Donde: ω = 5,0 rad/s
τ = 6,0 · 102 J
c) O trabalho é nulo, já que a citada força é perpendicular a cada deslocamento elementar sofrido pela esfera.
Respostas: a) 4,0 · 102 J; b) –1,0 · 102 J; c) 6,0 · 102 J
Respostas: a) 30 N; b) 5,0 rad/s; c) nulo
16 Na situação representada na figura, uma pequena esfera de
massa m = 2,4 kg realiza movimento circular e uniforme com velocidade angular ω em torno do ponto O. A circunferência descrita pela
esfera tem raio R = 30 cm e está contida em um plano horizontal. O
barbante que prende a esfera é leve e inextensível e seu comprimento
é L = 50 cm.
17 Um projétil de massa m é lançado obliquamente no vácuo, descrevendo a trajetória indicada abaixo:
B
g
h
A
C
Plano
horizontal
A altura máxima atingida é h e o módulo da aceleração da gravidade
vale g. Os trabalhos do peso do projétil nos deslocamentos de A até B,
de B até C e de A até C valem, respectivamente:
a) 0, 0 e 0.
d) m g h, –m g h e 0.
b) m g h, m g h e 2m g h.
e) Não há dados para os cálculos.
c) –m g h, m g h e 0.
g
L
R
Resolução:
τ = –m g h (trabalho resistente)
O
ω
A→B
τ = m g h (trabalho motor)
2
Sabendo que no local a influência do ar é desprezível e que g = 10 m/s ,
determine:
a) a intensidade da força de tração no barbante;
b) o valor de ω;
c) o trabalho da força que o barbante exerce sobre a esfera em
uma volta.
B→C
τ
A→C
=
τ
A→B
+ τ
B→C
τ=–mgh+mgh=0
A→C
Resposta: c
Tópico 6 – Trabalho e potência
18 O trabalho total realizado sobre uma partícula de massa
8,0 kg foi de 256 J. Sabendo que a velocidade inicial da partícula era de
6,0 m/s, calcule a velocidade final.
Resolução:
Teorema da Energia Cinética:
m v2f m v2i
–
τtotal =
2
2
8,0 2
256 =
(v – 6,02)
2 f
21 E.R. Um pequeno objeto de massa 2,0 kg, abandonado de um
ponto situado a 15 m de altura em relação ao solo, cai verticalmente
sob a ação da força peso e da força de resistência do ar. Sabendo que
sua velocidade ao atingir o solo vale 15 m/s, calcule o trabalho da
força de resistência do ar.
Dado: g = 10 m/s2
A (vA = 0)
Fr
15 m
P
B (vB = 15 m/s)
Donde: vf = 10 m/s
Resposta: 10 m/s
19 Uma partícula sujeita a uma força resultante de intensidade
2,0 N move-se sobre uma reta. Sabendo que entre dois pontos P e
Q dessa reta a variação de sua energia cinética é de 3,0 J, calcule a
distância entre P e Q.
Resolução:
(I) Teorema da Energia Cinética:
τ = Δ Ec = 3,0 J
P→Q
(II)
P→Q
τ = F d cos θ
P→Q
Resolução:
Aplicando o Teorema da Energia Cinética, temos:
τtotal = EcB – EcA
m v2B m v2A
τP + τF = 2 – 2
r
m v2B m v2A
m g h + τF = 2 – 2
r
Sendo m = 2,0 kg, g = 10 m/s2, h = 15 m, vA = 0 e vB = 15 m/s, calculemos o trabalho da força de resistência do ar (τ F ):
r
2,0 · (15)2
2,0 · 10 · 15 + τF =
⇒ 300 + τF = 225
2
r
r
τF = – 75 J
(θ = 0º e cos θ = 1 )
3,0 = 2,0 d (1)
r
O resultado negativo refere-se a um trabalho resistente.
d = 1,5 m
Resposta: 1,5 m
20 Uma partícula de massa 900 g, inicialmente em repouso na posição x0 = 0 de um eixo Ox, submete-se à ação de uma força resultante
paralela ao eixo. O gráfico abaixo mostra a variação da intensidade da
força em função da abscissa da partícula:
F (newtons)
15
10
5
0
2
4
6
8
x (metros)
Determine:
a) o trabalho da força de x0 = 0 a x1 = 6 m;
b) a velocidade escalar da partícula na posição x2 = 8 m.
Resolução:
a) τ = A1 + A2 + A3
x0 → x1
τ
x0 → x1
τ
(15 + 5) 2
+ 2 · 15 (J)
2
2
=2·5+
x 0 → x1
22 (Ufal) Um corpo de massa 6,0 kg é abandonado de uma altura
de 5,0 m num local em que g = 10 m/s2. Sabendo que o corpo chega ao
solo com velocidade de intensidade 9,0 m/s, calcule a quantidade de
calor gerada pelo atrito com o ar.
Resolução:
Teorema da Energia Cinética:
m v2f m v2i
–
τtotal =
2
2
m v2f
τ
m g h + Fr =
2
6,0 (9,0)2
τ
6,0 · 10 · 5,0 + Fr =
2
τF = – 57 J
r
Q = | τFr | = – 57 J
Resposta: 57 J
23 Na situação esquematizada, um halterofilista levanta 80 kg num
local em que g = 10 m/s2 e mantém o haltere erguido, como representa
a figura 2, durante 10 s.
= 45 J
b) Teorema da Energia Cinética:
m v22
m v20
τ = τ =
–
x →x
x →x
2
2
0
45 =
2
233
0
2,0 m
1
0,90 v22
⇒ v2 = 10 m/s
2
Respostas: a) 45 J; b) 10 m/s
Figura 1
Figura 2
234
PARTE II – DINÂMICA
Os trabalhos das forças musculares durante o levantamento do haltere
e durante sua manutenção no alto valem, respectivamente:
a) 800 J e 800 J.
b) 1 600 J e 1 600 J.
c) 800 J e zero.
d) 1 600 J e zero.
e) 1 600 J e 800 J.
Resolução:
τF = F AB cos 45°
2
(J)
τF = 10 · 2,0 2 ·
2
τF = 20 J
b) τP = –m g OA ⇒ τP = –2,0 · 10 · 2,0 (J)
Resolução:
τoper = m g h
τoper = 80 · 10 · 2,0 (J)
τP = – 40 J
Respostas: a) 20 J; b) – 40 J
τoper = 1600 J
O trabalho para manter o haltere suspenso é nulo, pois, durante essa
situação, não há deslocamento.
Resposta: d
24 (UFSC) Um helicóptero suspenso no ar, em repouso em relação
ao solo, ergue por meio de um cabo de aço, mantido vertical, uma caixa de massa igual a 200 kg que se desloca com velocidade constante
ao longo de um percurso de 10 m. No local, g = 10 m/s2. Sabendo que
no deslocamento citado as forças de resistência do ar realizam sobre a
caixa um trabalho de –1 400 J, calcule o trabalho da força aplicada pelo
cabo de aço sobre a caixa.
26 Um homem puxa a extremidade livre de uma mola de constante elástica igual a 1,0 · 103 N/m, alongando-a 20 cm. O trabalho
da força elástica da mola sobre a mão do homem vale:
a) 40 J.
b) 20 J.
c) – 40 J.
d) –20 J.
e) –2,0 · 105 J.
Resolução:
K (Δx)2
2
1,0 · 103 (0,20)2
tF = –
(J)
2
e
tF = –
e
tF = –20 J
e
Resolução:
Resposta: – 20 J
F
27 (Fuvest-SP) Considere um bloco de massa M = 10 kg que se
MRU
FC
move sobre uma superfície horizontal com uma velocidade inicial de
10 m/s. No local, o efeito do ar é desprezível e adota-se |g | = 10 m/s2.
a) Qual o trabalho realizado pela força de atrito para levar o corpo ao
repouso?
b) Supondo que o coeficiente de atrito cinético seja μ = 0,10, qual o
intervalo de tempo necessário para que a velocidade do bloco seja
reduzida à metade do seu valor inicial?
P
Teorema da Energia Cinética:
τ total = ΔFc
τF + τP + τF = 0
r
τF – 200 · 10 · 10 – 1400 = 0
Resolução:
a) Teorema da Energia Cinética:
at
τF = 21 400 J
2
2 m V
0
τF = m V –
2
2
at
Resposta: 21 400 J
τF = 0 –
at
25 Uma partícula, inicialmente em repouso no ponto A, é leva-
da ao ponto B da calha contida em um plano vertical, de raio igual a
2,0 m, indicada na figura. Uma das forças que agem sobre a partícula
é F , horizontal, dirigida sempre para a direita e de intensidade igual a
10 N. Considerando a massa da partícula igual a 2,0 kg e assumindo
g = 10 m/s2, determine:
O
0
r=
2,
m
B
g
F
A
a) o trabalho de F ao longo do deslocamento AB;
b) o trabalho do peso da partícula ao longo do deslocamento referido
no item anterior.
10 (10)2
⇒ τFat = –5,0 · 102 J
2
b) (I) Fat = µ Fn ⇒ Fat = µ m · g
2a Lei de Newton: Fat = m a
De (I) e (II), vem:
M a=µ M g
a = µ g ⇒ a = 0,10 · 10 (m/s2)
(I)
(II)
a = 1,0 m/s2
MUV:
V = V0 + α t
10 = 10 – 1,0 t ⇒
2
t = 5,0 s
Respostas: a) –5,0 · 102 J; b) 1,0 m/s2 e 5,0 s
Tópico 6 – Trabalho e potência
28 (Vunesp-SP) Um vagão, deslocando-se lentamente com veloci-
dade v num pequeno trecho plano e horizontal de uma estrada de ferro, choca-se com um monte de terra e pára abruptamente. Em virtude
do choque, uma caixa de madeira, de massa 100 kg, inicialmente em
repouso sobre o piso do vagão, escorrega e percorre uma distância de
2,0 m antes de parar, como mostra a figura.
Resolução:
F (N)
16
Monte de terra
2,0 m
100 kg
Considerando g = 10 m/s2 e sabendo que o coeficiente de atrito dinâmico entre a caixa e o piso do vagão é igual a 0,40, calcule:
a) a velocidade v do vagão antes de se chocar com o monte de terra;
b) a energia cinética da caixa antes de o vagão se chocar com o monte
de terra e o trabalho realizado pela força de atrito que atuou na
caixa enquanto ela escorregava.
Resolução:
m v2f m v2i
–
a) Teorema da Energia Cinética: τF =
2
2
at
2
m
v
µ Fn d cos 180° = 0 –
2
2
–µ m g d = – m v ⇒ v = 2 µ g d
2
2
·
0,40
·
10
·
2,0
v=
(m/s) ⇒ v = 4,0 m/s
2
100 (4,0)2
b) EC = m v ⇒ EC =
(J)
2
2
i
i
EC = 8,0 · 102 J
235
0
2,0
2,0 · 16
(I) τ = “área” =
= 16 J
2
2
2,0 v2
m v2 m v 0
⇒
(II) τ = 2 – 2 ⇒ 16 = 2
x (m)
v = 4,0 m/s
Resposta: 4,0 m/s
31 E.R. Um garoto de massa 40 kg partiu do repouso no ponto A
do tobogã da figura a seguir, atingindo o ponto B com velocidade de
10 m/s:
A
g
10 m
B
Admitindo |g | = 10 m/s2 e desprezando o efeito do ar, calcule o trabalho das forças de atrito que agiram no corpo do garoto de A até B.
i
τF = EC – EC ⇒ τF = 0 – EC
f
at
i
at
i
τF = – 8,0 · 102 J
at
Respostas: a) 4,0 m/s; b) 8,0 · 102 J e – 8,0 · 102 J
Resolução:
Durante a descida, três forças agem no corpo do garoto:
P = força da gravidade (peso);
Fn = reação normal do tobogã;
Fat = força de atrito.
Fat
Fn
29 Um projétil de 10 g de massa atinge horizontalmente uma parede
de alvenaria com velocidade de 120 m/s, nela penetrando 20 cm até
parar. Determine, em newtons, a intensidade média da força resistente
que a parede opõe à penetração do projétil.
Resolução:
Teorema da Energia Cinética:
2
m v20
τF = m v –
2
2 m v2
r
0
Fr d cos 180° = 0 –
2
10 · 10–3 (120)2
–Fr 0,20 = –
2
P
O trabalho total, de todas as forças, é dado por:
τtotal = τP + τF + τF
at
n
A parcela τF é nula, pois Fn é, a cada instante, perpendicular à trajen
tória. Assim:
τtotal = τP + τF
(I)
at
Donde:
2
Fr = 3,6 · 10 N
Resposta: 3,6 · 102 N
30 (Mack-SP) Um corpo de massa 2,0 kg é submetido à ação de
uma força cuja intensidade varia de acordo com a equação F = 8,0x.
F é a força medida em newtons e x é o deslocamento dado em metros.
Admitindo que o corpo estava inicialmente em repouso, qual a intensidade da sua velocidade após ter-se deslocado 2,0 m?
Conforme o Teorema da Energia Cinética, temos que:
τtotal = E CB – E CA
m v2B m v2A
–
2
2
Como vA = 0 (o garoto partiu do repouso), vem:
τtotal =
m v2
τtotal = 2 B
(II)
236
PARTE II – DINÂMICA
Comparando (I) e (II), obtém-se:
m v2B
m v2B
τP + τF =
⇒ m g h + τF =
2
2
at
at
m v2B
τF =
–mgh
2
at
Sendo m = 40 kg, vB = 10 m/s e g = 10 m/s2, calculemos τF :
at
2
τF = 40 · (10) – 40 · 10 · 10 (J)
2
at
τ = – 2,0 · 103 J
Donde:
Fat
A
32 Uma esfera de massa 1,0 kg, lançada com velocidade de 10 m/s
no ponto R da calha vertical, encurvada conforme a figura, atingiu o
ponto S, por onde passou com velocidade de 4,0 m/s:
S
g
2,0 m
R
Sabendo que no local do experimento |g | = 10 m/s2, calcule o trabalho das forças de atrito que agiram na esfera no seu deslocamento
de R até S.
Resolução:
Teorema da Energia Cinética:
m v2S m v2R
–
τtotal =
2
2
m v2S m v2R
τ F + τP =
–
2
2
at
1,0
τF – 1,0 · 10 · 2,0 =
(4,02 · 102)
2
at
Donde:
34 Na situação esquematizada na figura, a mola tem massa desprezível, constante elástica igual a 1,0 · 102 N/m e está inicialmente travada
na posição indicada, contraída de 50 cm. O bloco, cuja massa é igual a
1,0 kg, está em repouso no ponto A, simplesmente encostado na mola.
O trecho AB do plano horizontal é perfeitamente polido e o trecho BC
é áspero.
2,0 m
5,0 m
C
Em determinado instante, a mola é destravada e o bloco é impulsionado, atingindo o ponto B com velocidade de intensidade VB. No local, a
influência do ar é desprezível e adota-se g = 10 m/s2. Sabendo que o
bloco para ao atingir o ponto C, calcule:
a) o valor de VB;
b) o coeficiente de atrito cinético entre o bloco e o plano de apoio no
trecho BC.
Resolução:
a) Teorema da Energia Cinética:
m v2B m v2A
τF =
–
2
2
e
K (Δx)2 m 2 2
=
(v – v )
2 B A
2
2
2
1,0 · 10 · (0,50) = 1,0 · (v2B – 0) ⇒
vB = 5,0 m/s
b) Teorema da Energia Cinética:
m v2C m v2B
τF =
–
2
2
at
v2B
m v2B
–µ m g d = 0 –
⇒ µ=
2 g d
2
(5,0)2
µ=
⇒ µ = 0,25
2 · 10 · 5,0
τF = – 22 J
Respostas: a) 5,0 m/s; b) 0,25
at
Resposta: – 22 J
35 (Olimpíada Brasileira de Física) Um servente de pedreiro, empre-
33 (Fuvest-SP) Um bloco de massa 2,0 kg é lançado do topo de um
plano inclinado, com velocidade escalar de 5,0 m/s, conforme indica a figura. Durante a descida, atua sobre o bloco uma força de atrito constante de intensidade 7,5 N, que faz o bloco parar após deslocar-se 10 m.
Calcule a altura H, desprezando o efeito do ar e adotando g = 10 m · s–2.
gando uma pá, atira um tijolo verticalmente para cima para o mestre-de-obras, que está em cima da construção. Veja a figura. Inicialmente,
utilizando a ferramenta, ele acelera o tijolo uniformemente de A para
B; a partir de B, o tijolo se desliga da pá e prossegue em ascensão vertical, sendo recebido pelo mestre-de-obras com velocidade praticamente nula em C.
A
C
v
10 m
H
B
Resolução:
Teorema da Energia Cinética:
m v2A
τtotal = EC – EC ⇒ m g H – Fat d = 0 –
2
B
A
2,0 · (5,0)2
H = 2,5 m
⇒
2,0 · 10 H – 7,5 · 10 = –
2
Resposta: 2,5 m
B
B
A
Tópico 6 – Trabalho e potência
Considerando-se como dados o módulo da aceleração da gravidade, g,
a massa do tijolo, M, e os comprimentos, AB = h e AC = H, e desprezando-se a influência do ar, determine:
a) a intensidade F da força com a qual a pá impulsiona o tijolo;
b) o módulo a da aceleração do tijolo ao longo do percurso AB.
Resolução:
a) Teorema da Energia Cinética:
τtotal = EC – EC
C
A
M v2C M v2A
τF + τP =
–
⇒ F h–M g H=0 ⇒
2
2
F=
M g H
h
K (Δx)2
K (0,050)2
⇒ –5,0 = –
2
2
Donde: K = 4,0 · 103 N/m
c) τFe = –
Respostas: a) 5,0 J; b) – 5,0 J; c) 4,0 · 103 N/m
37 Uma partícula de massa 2,0 kg, inicialmente em repouso sobre o
solo, é puxada verticalmente para cima por uma força F, cuja intensidade varia com a altura h, atingida pelo seu ponto de aplicação, conforme
mostra o gráfico:
F (N)
32
b) 2a Lei de Newton:
M g H
F–P=M a ⇒
–M g=M a
h
24
16
H
–1 g
a=
h
Donde:
8,0
0
M g H
H
Respostas: a) F =
; b) a =
–1 g
h
h
36 Na situação representada nas figuras 1 e 2, a mola tem massa
desprezível e está fixa no solo com o seu eixo na vertical. Um corpo de
pequenas dimensões e massa igual a 2,0 kg é abandonado da posição
A e, depois de colidir com o aparador da mola na posição B, aderindo a
ele, desce e pára instantaneamente na posição C.
A
1,0 2,0 3,0 4,0 5,0 6,0 h (m)
No local, |g | = 10 m · s–2 e despreza-se a influência do ar. Considerando
a ascensão da partícula de h0 = 0 a h1 = 6,0 m, determine:
a) a altura em que a velocidade tem intensidade máxima;
b) a intensidade da velocidade para h1 = 6,0 m.
Resolução:
a) F = 32 – 24 h ⇒ F = 32 – 4,0 h (SI)
6,0
A velocidade é máxima quando
|F | = |P | = m · g, isto é, |F | = 2,0 · 10 = 20 N
Logo: 20 = 32 – 4,0 · h ⇒
20 cm
5,0 cm
C
Figura 1
h = 3,0 m
b) Teorema da Energia Cinética:
m v21 m v20
–
τtotal =
2
2
m v21
m v21
τF + τP =
⇒ “área” – m g h =
2
2
2,0 · v21
(32 + 8,0) · 6,0
v1 = 0
– 2,0 · 10 · 6,0 =
⇒
2
2
B
Figura 2
Adotando g = 10 m/s2 e desprezando o efeito do ar e a energia mecânica dissipada no ato da colisão, calcule:
a) o trabalho do peso do corpo no percurso AC;
b) o trabalho da força aplicada pela mola sobre o corpo no percurso BC;
c) a constante elástica da mola.
Resolução:
a) τP = m g h ⇒ τP = 2,0 · 10 · 0,25 (J)
Respostas: a) 3,0 m; b) 0
38 Nas duas situações representadas abaixo, uma mesma carga de
peso P é elevada a uma mesma altura h:
h
Situação 1
α
τP = 5,0 J
b) Teorema da Energia Cinética:
m v2C m v2A
–
τtotal =
2
2
τP + τFe = 0 ⇒ τFe = –τP
τFe = –5,0 J
237
h
Situação 2
238
PARTE II – DINÂMICA
Nos dois casos, o bloco parte do repouso, parando ao atingir a altura h.
Desprezando todas as forças passivas, analise as proposições seguintes:
I. Na situação 1, a força média exercida pelo homem é menos intensa
que na situação 2.
II. Na situação 1, o trabalho realizado pela força do homem é menor
que na situação 2.
III. Em ambas as situações, o trabalho do peso da carga é calculado por
–P h.
IV. Na situação 1, o trabalho realizado pela força do homem é calculado por P h.
Responda mediante o código:
a) Todas são corretas.
d) Somente I, III e IV são corretas.
b) Todas são incorretas.
e) Somente III é correta.
c) Somente II e III são corretas.
40 Considere uma tora de madeira de massa igual a
2,0 · 10 2 kg, cilíndrica e homogênea, posicionada sobre o solo,
conforme indica a f igura.
Resolução:
(I) Correta.
(II) Incorreta.
Em ambos os casos:
τtotal = ΔEC
τoper + τP = 0 ⇒ τoper – P h = 0
Resolução:
τoper = m g h
3,0 m
0,50 m
Adotando g = 10 m · s–2, calcule o trabalho realizado por um grupo
de pessoas para colocar a tora com o eixo longitudinal na vertical,
apoiada sobre sua base.
h é a elevação do centro de massa da tora.
h = 1,5 – 0,25 = 1,25 m
τoper = 2,0 · 102 · 10 · 1,25 (J)
τoper = 2,5 · 103 J
τoper = P h
(III) Correta.
(IV) Correta.
Resposta: 2,5 · 103 J
Resposta: d
41 Na figura, um operário ergue um balde cheio de concreto, de
39 E.R. Considere um corpo de massa 20 kg, homogêneo, em for-
ma de paralelepípedo, como ilustrado abaixo.
20 kg de massa, com velocidade constante. A corda e a polia são ideais
e, no local, g = 10 m/s2. Considerando um deslocamento vertical de 4,0
m, que ocorre em 25 s, determine:
0,50 m
2,0 m
2,0 m
0,50 m
g
Figura 2
Figura 1
O corpo, inicialmente apoiado sobre sua maior face (figura 1), é erguido
por um operador, ficando apoiado sobre sua menor face (figura 2).
Sendo g = 10 m · s–2, calcule o trabalho da força do operador no erguimento do corpo.
Resolução:
Observe que este é um corpo extenso, de dimensões não-desprezíveis.
Para efeito de cálculo vamos considerar o seu centro de massa, ou seja,
o ponto CM onde se admite concentrada toda a massa do sistema.
CM
CM
CM
a) o trabalho realizado pela força do operário;
b) a potência média útil na operação.
Resolução:
a) τoper = m g h
τoper = 20 · 10 · 4,0 (J)
τoper = 8,0 · 102 J
1,0 m
0,25 m
b) Potm =
τoper
Sendo m = 20 kg, g = 10 m · s–2 e h = 1,0 – 0,25 = 0,75 m, calculamos
o trabalho pedido (τoper):
Δt
8,0 · 102 J
Potm =
25 s
τoper = m g h ⇒ τoper = 20 · 10 · 0,75 (J)
Potm = 32 W
τoper = 1,5 · 102 J
Respostas: a) 8,0 · 102 J ; b) 32 W
Tópico 6 – Trabalho e potência
42 (PUC-SP) Uma pessoa de massa 80 kg sobe uma escada de
20 degraus, cada um com 20 cm de altura.
a) Calcule o trabalho que a pessoa realiza contra a gravidade (adote
g = 10 m/s2).
b) Se a pessoa subir a escada em 20 segundos, ela se cansará mais do
que se subir em 40 segundos. Como se explica isso, já que o trabalho realizado é o mesmo nos dois casos?
Resolução:
a) τoper = m g h
τoper = 80 · 10 · 20 · 0,20 (J)
239
46 (Fuvest-SP) Uma esteira rolante transporta 15 caixas de bebida
por minuto de um depósito no subsolo até o andar térreo. A esteira
tem comprimento de 12 m, inclinação de 30° com a horizontal e
move-se com velocidade constante. As caixas a serem transportadas já são colocadas com a mesma velocidade da esteira. Se cada
caixa pesa 200 N, o motor que aciona esse mecanismo deve fornecer a potência de:
e) 1,0 · 103 W.
a) 20 W.
c) 3,0 · 102 W.
b) 40 W.
d) 6,0 · 102 W.
Resolução:
τoper = 3,2 · 10 J
3
12
b) A pessoa se cansará mais, pois dispenderá em 20 s uma potência
maior que em 40 s.
h
Respostas: a) 3,2 · 103 J; b) A pessoa se cansará mais, pois dispenderá em 20 s uma potência maior que em 40 s.
43 (Fuvest-SP) Dispõe-se de um motor com potência útil de
200 W para erguer um fardo de massa de 20 kg à altura de 100 m em
um local onde g = 10 m/s2.
Supondo que o fardo parte do repouso e volta ao repouso, calcule:
a) o trabalho desenvolvido pela força aplicada pelo motor;
b) o intervalo de tempo gasto nessa operação.
Resolução:
a) τ = m g h ⇒ τ = 20 · 10 · 100 (J)
m
30°
(I) sen 30° = h
12
0,50 = h ⇒
12
h = 6,0 m
(II) Potm = τ = P h
Δt Δt
15 · 200 · 6,0 J
Potm =
60
s
Potm = 3,0 · 102 W
τ = 2,0 · 104 J
4
b) Potm = τ ⇒ 200 = 2,0 · 10
Δt
Δt
Δt = 100 s = 1 min 40 s
4
Respostas: a) 2,0 · 10 J; b) 1 min 40 s
44 Dentre as unidades seguintes, aponte aquela que não pode ser
Resposta: c
47 (Unicamp-SP) Um carro recentemente lançado pela indústria
brasileira tem aproximadamente 1,5 tonelada e pode acelerar, sem
derrapagens, do repouso até uma velocidade escalar de 108 km/h, em
10 segundos.
(Fonte: Revista Quatro Rodas.)
utilizada na medição de potências.
d) quilowatt-hora
a) kg · m2 · s–3
m
e) J · s–1
b) N ·
s
c) cavalo-vapor
Despreze as forças dissipativas e adote 1 cavalo-vapor (cv) = 750 W.
a) Qual o trabalho realizado, nessa aceleração, pelas forças do motor
do carro?
b) Qual a potência média do motor do carro em cv?
Resolução:
Quilowatt-hora (kWh) é unidade de energia geralmente utilizada em
avaliações de consumo de energia elétrica.
Resolução:
a) Teorema da Energia Cinética:
2
m v20
1,5 · 103 · (30)2
⇒ τ=
(J)
τ= m v –
2
2
2
Resposta: d
τ = 6,75 · 105 J
45 (UFPE) Um homem usa uma bomba manual para extrair água
de um poço subterrâneo a 60 m de profundidade. Calcule o volume de
água, em litros, que ele conseguirá bombear caso trabalhe com potência constante de 50 W durante 10 minutos. Despreze todas as perdas e
adote g = 10 m/s2 e a densidade da água igual a 1,0 kg/艎.
Resolução:
m g h
⇒ 50 = m 10 · 60
Potm = τ =
Δt
10 · 60
Δt
m = 50 kg ⇒
V = 50 litros
Resposta: 50 litros
6,75 · 105
b) Potm = τ ⇒ Potm =
(cv)
10 · 750
Δt
Potm = 90 cv
Respostas: a) 6,75 · 105 J; b) 90 cv
48 O gráfico a seguir mostra a variação da intensidade de uma das
forças que agem em uma partícula em função de sua posição sobre
uma reta orientada. A força é paralela à reta.
Sabendo que a partícula tem movimento uniforme com velocidade
de 4,0 m/s, calcule, para os 20 m de deslocamento descritos no gráfico a seguir:
240
PARTE II – DINÂMICA
Considere a densidade da água igual a 1,0 · 103 kg/m3, adote
g = 10 m/s2 e admita que não haja dissipação de energia mecânica.
F (N)
40
20
0
A
118 m
5,0
10
15
20 d (m)
a) o trabalho da força;
b) sua potência média.
Resolução:
τ = A1 + A 2
τ=
(10 + 5,0) 20
+ 20 · 20 (J)
2
τ = 5,5 · 102 J
5,5 · 102 · 4,0
b) Potm = τ = τ ⇒ Potm =
(W)
20
Δt d
v
Potm = 1,1 · 102 W
Gerador
B
Calcule, em MW, a potência hídrica na entrada do gerador.
Resolução:
Potm = µ Z g h
Potm = 1,0 · 103 · 5,0 · 102 ·10 · 118 (W)
Potm = 590 MW
Professor: compare Xingó com Itaipu (exercício anterior).
Resposta: 590 MW
51 No esquema seguinte, F é a força motriz que age no carro e v ,
sua velocidade vetorial instantânea:
Respostas: a) 5,5 · 102 J; b) 1,1 · 102 W
v
F
49 A usina hidrelétrica de Itaipu é uma obra conjunta do Brasil e do
Paraguai que envolve números gigantescos. A potência média teórica
chega a 12 600 MW quando 18 unidades geradoras operam conjuntamente, cada qual com uma vazão próxima de 700 m3 por segundo.
Suponha que a água da represa adentre as tubulações que conduzem o
líquido às turbinas com velocidade praticamente nula e admita que os
geradores aproveitem 100% da energia hídrica disponível. Adotando-se para a aceleração da gravidade o valor 10 m/s2 e sabendo-se que a
densidade da água é igual a 1,0 · 103 kg/m3, determine o desnível entre
as bocas das tubulações e suas bases, onde estão instaladas as turbinas
das unidades geradoras.
Resolução:
A potência elétrica disponibilizada em cada unidade geradora é calculada fazendo-se:
Potm = 12 600 M W = 700 M W = 7,0 · 108 W
18
Sendo µ = 1,0 · 103 kg/m3, Z = 7,0 · 102 m3/s e g = 10 m/s2, calculemos
o desnível h.
Potm = µ Z g h ⇒ 7,0 · 108 = 1,0 · 103 · 7,0 · 102 · 10 h
Sendo | F | = 1,0 · 103 N e |v | = 5,0 m/s, calcule, em kW, a potência de F
no instante considerado.
Resolução:
Pot = F v cos θ
( θ = 0º e cos θ = 1 )
Pot = F v ⇒ Pot = 1,0 · 103 · 5,0 (W)
Pot = 5,0 · 103 W = 5,0 kW
Resposta: 5,0 kW
52 Uma partícula de massa 2,0 kg parte do repouso sob a ação de
uma força resultante de intensidade 1,0 N. Determine:
a) o módulo da aceleração adquirida pela partícula;
b) a potência da força resultante, decorridos 4,0 s da partida.
Donde: h = 100 m
Resolução:
a) 2a Lei de Newton:
F = m a ⇒ 1,0 = 2,0 a
Resposta: 100 m
a = 0,50 m/s2
50 (UFPE) As águas do rio São Francisco são represadas em muitas
barragens, para o aproveitamento do potencial hidrográfico e transformação de energia potencial gravitacional em outras formas de energia.
Uma dessas represas é Xingó, responsável por grande parte da energia
elétrica que consumimos. A figura a seguir representa a barragem e
uma tubulação, que chamamos de tomada d’água, e o gerador elétrico. Admita que, no nível superior do tubo, a água está em repouso,
caindo a seguir até um desnível de 118 m, onde encontra o gerador de
energia elétrica. O volume de água que escoa, por unidade de tempo,
é de 5,0 · 102 m3/s.
b) MUV: v = v0 + αt
v = 0,50 · 4,0 (m/s)
v = 2,0 m/s
Pot = F v cos θ
(θ = 0º e cos θ = 1)
Pot = 1,0 · 2,0 (W)
Pot = 2,0 W
Respostas: a) 0,50 m/s2; b) 2,0 W
Tópico 6 – Trabalho e potência
53 No arranjo da figura, o homem faz com que a carga de peso
igual a 300 N seja elevada com velocidade constante de 0,50 m/s.
241
55 O diagrama seguinte representa a potência instantânea fornecida por uma máquina, desde t0 = 0 s até t1 = 30 s:
Pot (103 W)
2,0
1,0
0
Considerando a corda e a polia ideais e o efeito do ar desprezível,
determine:
a) a intensidade da força com que o homem puxa a corda;
b) a potência útil da força exercida pelo homem.
Resolução:
a)
10
30 t (s)
Com base no diagrama, determine:
a) o trabalho realizado pela máquina, de t0 = 0 s até t1 = 30 s;
b) a potência média fornecida pela máquina no intervalo referido no
item anterior.
Resolução:
a) τ = A1 + A2 + A3
F
t0 → t 1
MRU
τ
(2,0 + 1,0) 103 · 10
+ 10 · 2,0 · 103 (W)
2
= 10 · 1,0 · 103 +
t0 → t 1
τ = 4,5 · 104 J
Donde:
P
t 0 → t1
F = P; logo:
τ
F = 300 N
t 0 → t1
b) Potm =
b) Pot = F v cos θ
(θ = 0º e cos θ = 1)
Pot = 300 · 0,50 (W)
Δt
4,5 · 104
30
Potm =
(W)
Potm = 1,5 · 103 W
Pot = 150 W
Respostas: a) 4,5 · 104 J; b) 1,5 · 103 W
Respostas: a) 300 N; b) 150 N
54 (UFPE) Um gerador elétrico suposto ideal é acionado pela queda
de um bloco de massa M que desce sob a ação da gravidade com velocidade escalar constante de 5,0 m/s. Sabendo que a potência fornecida
pelo gerador é usada para acender uma lâmpada de 100 W, calcule o
valor de M.
56 Uma caixa de massa 5,0 · 102 kg é erguida verticalmente por um
guindaste, de modo que sua altura em relação ao solo varia em função
do tempo, conforme o gráfico abaixo:
h (m)
4,0
2,0
Gerador
0
g
20
M
–2
Despreze os atritos e adote |g | = 10 m · s .
Resolução:
Num processo ideal, a potência do peso do bloco em sua descida é
totalmente transferida para a lâmpada.
Pot(P) = Potlâmpada = 100 W
M · 10 · 5,0 = 100
Donde: M = 2,0 kg
Resposta: M = 2,0 kg
4,0
2
8,0 t (s)
Considerando |g | = 10 m/s , analise as proposições seguintes:
I. O movimento da caixa é uniforme.
II. A velocidade escalar da caixa no instante t = 5,0 s vale 5,0 · 10–1 m/s.
III. A força que os cabos do guindaste aplicam na caixa tem intensidade 5,0 · 103 N.
IV. A potência útil do guindaste é de 2,5 kW.
Responda conforme o código:
a) Todas são corretas.
b) Todas são incorretas.
c) Somente I e II são corretas.
d) Somente III e IV são corretas.
e) Somente I, III e IV são corretas.
242
PARTE II – DINÂMICA
b) MRU: Fm = Pt = 3,4 · 103 N
Pot(F ) = Fm v cos β (β é o ângulo formado entre Fm e v )
m
(β = 0° e cos β = 1)
Resolução:
I. Correta.
O gráfico h = f(t) é uma rede oblíqua.
II. Correta.
v = Δh ⇒ v = 4,0 m
8,0 s
Δt
Pot(F ) = 3,4 · 103 · 10 (1) (W) ⇒
m
Pot(F ) = 34 kW
m
–1
v = 5,0 · 10 m/s
III. Correta.
F=P⇒F=mg
F = 5,0 · 102 · 10 (N) ⇒ F = 5,0 · 103 N
IV. Correta.
Pot = F v ⇒ Pot = 5,0 · 103 · 5,0 · 10–1 (W)
Pot = 2,5 · 103 W = 2,5 kW
Respostas: a) – 6,8 · 104 J; b) 34 kW
59 Uma caminhonete de massa 1,2 tonelada sobe uma rampa inclinada de 30° em relação à horizontal, com velocidade constante de
intensidade 36 km/h. As forças de atrito, resistentes ao movimento,
perfazem 25% do peso do veículo. Adotando g = 10 m/s2, calcule:
a) a intensidade da força motriz exercida na caminhonete;
b) a potência útil desenvolvida pelo motor do veículo.
Resposta: a
57 Um paraquedista desce com velocidade constante de 5,0 m/s.
O conjunto paraquedas e paraquedista pesa 100 kgf. Considerando
g = 9,8 m/s2, podemos dizer que a potência dissipada pelas forças de
resistência do ar tem módulo:
a) 0,50 kW. b) 4,9 kW. c) 5,0 kW. d) 49 kW. e) 50 kW.
Resolução:
a)
F
U
MR
Fr
Resolução:
(I) MRU: Fr = P ⇒ Fr = m g
Como g = 9,8 m/s2 (valor normal), tem-se m = 100 kg; logo:
Fr = 100 · 9,8 (N) ⇒
Pt
θ = 30°
Fr = 980 N
MRU: F = Fr + Pt ⇒ F = 0,25 m g + m g sen θ
F = 0,25 m g + 0,5 m g
F = 0,75 m g ⇒ F = 0,75 · 1,2 · 10 (kN)
(II) Pot = Fr v cos θ
(θ = 180° e cos θ = –1)
Pot = 980 · 5,0 (–1) (W)
Pot = – 4 900 W = – 4,9 kW
F = 9,0 kN
Resposta: b
58 (Fatec-SP) Um carro de massa 1,0 tonelada sobe 20 m ao lon-
go de uma rampa inclinada de 20° com a horizontal, mantendo velocidade constante de 10 m/s. Adotando g = 10 m/s2, sen 20° = 0,34 e
cos 20° = 0,94 e desprezando o efeito do ar, calcule, nesse deslocamento:
a) o trabalho realizado pelo peso do carro;
b) a potência útil do motor.
Resolução:
a)
b) Pot = F v cos α
(α = 0° e cos α = 1)
Pot = 9,0 · 36 (kW)
3,6
Pot = 90 kW
Respostas: a) 9,0 kN; b) 90 kW
60 Sabe-se que a intensidade da força total de resistência recebida
U
MR
Fm
Pt
θ = 20°
(I) Pt = m g sen θ
Pt = 1,0 · 103 · 10 · 0,34 (N)
Pt = 3,4 · 103 N
(II) τP = Pt d cos α (α é o ângulo entre Pt e d )
(α = 180° e cos α = –1)
τP = 3,4 · 103 · 20 (–1) (J)
τP = – 6,8 · 104 J
por um carro de Fórmula 1 em movimento sobre o solo plano e horizontal é diretamente proporcional ao quadrado da intensidade de sua
velocidade.
Admita que, para manter o carro com velocidade VA = 140 km/h, o motor forneça uma potência útil PA = 30 HP. Que potência útil PB deverá o
motor fornecer para manter o carro com velocidade VB = 280 km/h?
Resolução:
F = Fr = k v2
Pot = F v = k v2 v ⇒
Pot = k v3
PA = k V3A ⇒ 30 = k (140)3
PB = k V2B ⇒ PB = k (280)3
Resposta: 240 HP
PB
= 280
30 140
3
⇒
PB = 240 HP
Tópico 6 – Trabalho e potência
61 E.R. A velocidade escalar (v) de uma partícula em trajetória
retilínea varia com o tempo (t), conforme a função:
v = 4,0t (SI)
Sabendo que a massa da partícula vale 3,0 kg, determine:
a) a expressão da potência instantânea da força resultante que age
na partícula;
b) o valor da potência no instante t = 2,0 s.
243
Desprezando o efeito do ar e supondo que a força referida seja paralela à mesa, determine:
a) o trabalho da força sobre o bloco de t0 = 0 s até t1 = 40 s;
b) o módulo da velocidade do bloco no instante t1 = 40 s.
Resolução:
a) O trabalho é calculado pela “área” A destacada abaixo:
Pot (W)
Resolução:
Analisando a função v = 4,0t, concluímos que o movimento é uniformemente variado, com aceleração de intensidade 4,0 m/s2.
Aplicando a 2a Lei de Newton, obtemos a intensidade da força que
acelera a partícula:
100
A
F = m a ⇒ F = 3,0 · 4,0 (N)
0
20
F = 12 N
a) Como a força resultante tem a mesma orientação da velocidade,
sua potência fica dada por:
Como F = 12 N e v = 4,0t, vem:
Pot = 48t
τ = 3,0 · 103 J
m v240 m v20
–
2
2
Sendo m = 15 kg, v0 = 0 e τ = 3,0 · 103 J, calculemos v40:
(SI)
τ=
b) Para t = 2,0 s, temos:
Pot = 48 · 2 (W) ⇒
Pot = 96 W
3,0 · 103 =
62 Sob a ação de uma força resultante constante e de intensidade 20 N, uma partícula parte do repouso, adquirindo um movimento cuja função das velocidades escalares é v = 2k t (SI), sendo k
uma constante adimensional e positiva. Sabendo que, no instante
t = 1 s, a potência da força resultante sobre a partícula vale 200 W,
determine o valor de k.
Resolução:
Pot = F v ⇒ Pot = 20 · 2 k t
Pot = 40 k t
200 = 40 k 1
15 v240
⇒
2
v40 = 20 m/s
64 O gráfico abaixo mostra a variação da potência instantânea da
força resultante em uma partícula de massa 2,0 kg que, no instante
t0 = 0, tem velocidade escalar igual a 1,0 m/s.
Pot (W)
20
10
0
k=5
Resposta: 5
63 E.R. Um bloco de 15 kg de massa repousa sobre uma mesa
horizontal e sem atrito. No instante t0 = 0 s, passa a agir sobre ele uma
força cuja potência é dada em função do tempo, conforme o gráfico
seguinte:
1,0
2,0
3,0
4,0
Resolução:
a) Potm]50 =
τ]50 “área”
=
Δt
Δt
(5,0 + 3,0) 20
(W) ⇒ Potm]50 = 16 W
2 · 5,0
m v25 m v20
b) τ]50 =
–
2
2
m
“área” =
(v25 – v20)
2
2,0 2
80 =
(v5 – 1,02) ⇒ v5 = 9,0 m/s
2
20
40
t (s)
5,0 t (s)
Supondo que a trajetória seja retilínea, calcule:
a) a potência média da força resultante, no intervalo de t0 = 0 a t1 = 5,0 s;
b) a velocidade escalar da partícula no instante t1 = 5,0 s.
Potm]50 =
Pot (W)
100
0
t (s)
b) A força em questão é a resultante sobre o bloco, o que nos permite aplicar o Teorema da Energia Cinética:
τ = Ec40 – Ec0
Pot = F v
Pot = 12 · 4,0t ⇒
40
(40 + 20)100
τ=A=
(J)
2
Respostas: a) 16 W; b) 9,0 m/s
244
PARTE II – DINÂMICA
65 (Esc. Naval-RJ – mod.) Um corpo de 2,0 kg de massa, ini-
cialmente em repouso sobre um plano horizontal, sob a ação de
seu peso e da força de contato com o plano, é empurrado por uma
força F horizontal constante, de intensidade 12 N, conforme representa a figura. Sabe-se que os coeficientes de atrito cinético e estático entre o corpo e o plano são, respectivamente, 0,10 e 0,20. A aceleração da gravidade no local é 10 m/s2 e desprezam-se os efeitos do
ar. O trabalho, em joule, realizado pela força F durante os dois primeiros segundos da aplicação da força F é:
2
(II) ΔEC = 2 M V ⇒ ΔEC = M F t
2
2 M
ΔEC =
2
(F t)2
4 M
Resposta: d
67 Na figura, AB é um plano inclinado sem atrito e BC é um plano
horizontal áspero. Um pequeno bloco parte do repouso no ponto A e
para no ponto C:
F
A
a) 64.
b) 80.
c) 96.
d) 100.
e) 120.
Resolução:
(I) Fat = µe Fn = µe m g
d
Fat = 0,20 · 2,0 · 10 = 4,0 N
C
Fat = µC Fn = µC mg
C
Fat = 0,10 · 2,0 · 10 = 2,0 N
2,0 m
C
B
Sabendo que o coeficiente de atrito cinético entre o bloco e o plano
BC vale 0,40 e que a influência do ar é desprezível, calcule a distância
percorrida pelo bloco nesse plano.
C
(II) 2a Lei de Newton:
F – Fat = m a
C
12 – 2,0 = 2,0 a ⇒ a = 5,0 m/s2
5,0
(III) MUV: d = v0 t + a t2 ⇒ d =
(2,0)2 (m)
2
2
d = 10 m
(IV) τ = F d ⇒ τ = 12 ·10 (J)
τ = 120 J
Resolução:
Teorema da Energia Cinética:
m v2C m v2A
–
τ=
2
2
A→C
τ
τP + F = 0
at
A→C
B→C
m g h – µC m g d = 0
2,0
d= h ⇒ d=
(m)
µC
0,40
d = 5,0 m
Resposta: e
Resposta: 5,0 m
66 (Umesp-SP) Dois blocos de massa M cada um, inicialmente em
repouso, sobre uma superfície lisa, são submetidos a uma força constante de módulo F, conforme mostra a figura, por um intervalo de tempo t. Desprezando-se a influência do ar, podemos calcular a velocidade
final V e a variação da energia cinética ΔEc desses blocos, respectivamente, nesse intervalo de tempo, pelas relações:
F
M
M
68 (Fuvest-SP) Dois pequenos corpos, 1 e 2, movem-se em um plano horizontal, com atrito desprezível, em trajetórias paralelas, inicialmente com mesma velocidade, de módulo V0. Em dado instante, os
corpos passam por uma faixa rugosa do plano, de largura d. Nessa
faixa, o atrito não pode ser desprezado e os coef icientes de atrito
cinético entre o plano rugoso e os corpos 1 e 2 valem μ1 e μ2 respecV
V
tivamente. Os corpos 1 e 2 saem da faixa com velocidades 0 e 0
2
3
respectivamente.
Faixa rugosa
4(F t)2
a) V = F t ; ΔEc =
.
2M
M
(F t)2
d) V = F t ; ΔEc =
.
2M
4M
(F t)2
.
b) V = 2F t ; ΔEc =
M
4M
(F t)2
e) V = F t ; ΔEc =
.
4M
2M
V0
V0
(F t)2
.
c) V = F t ; ΔEc =
M
2M
Resolução:
(I) 2a Lei de Newton: F = 2 M a ⇒ F = 2 M V
t
V= F t
2 M
V0
3
d
Nessas condições, a razão
a) 2 .
3
4
b) .
9
μ1
é igual a:
μ2
c) 27 .
32
d) 16 .
27
e) 1 .
2
V0
2
Tópico 6 – Trabalho e potência
Resolução:
Corpo 1: Teorema da Energia Cinética:
m1 v21 m1 v20
–
2
2
m
–µ1 m1 g d = 1
2
70 (Mack-SP) Um bloco de peso igual a 10 N parte do repouso e
sobe a rampa indicada na figura 1 mediante a aplicação da força F, de
direção constante e cuja intensidade varia com a abscissa x, de acordo
com o gráfico da figura 2. O trabalho de O até A realizado pelo atrito
existente entre o bloco e a rampa é igual a 10 J, em valor absoluto.
Adote g = 10 m · s–2. Nessas condições, a velocidade do bloco, ao atingir
o ponto culminante A, é igual a:
τ1 =
v0 2 2
– v0
2
Donde: µ1 g d = 3 v20
8
(I)
A
Corpo 2: Teorema da Energia Cinética:
Figura 1
m v2 m v2
τ2 = 2 2 – 2 0
2
2
m
–µ2 m2 g d = 2
2
F (N)
Figura 2
25
v0 2 2
– v0
3
µ2 g d = 4 v20
(II)
9
Donde:
245
x
4m
F
O
Dividindo (I) por (II), temos:
0
3m
µ1 3 9
= ·
µ2 8 4
a) 2 m · s–1.
b) 5 m · s–1.
µ1 27
=
µ2 32
Resolução:
1
c) 6 m · s–1.
d) 10 m · s–1.
2
3
4
5 x (m)
e) 15 m · s–1.
F
Resposta: c
P
69 (UFU-MG – mod.) Um menino e seu skate, considerados uma
única partícula, deslizam numa pista construída para esse esporte,
como representado na figura abaixo. A parte plana e horizontal da pista mede 2,0 m e o menino parte do repouso do ponto A, cuja altura,
em relação à base, é de 1,0 m. Considerando-se que há atrito somente
na parte plana da pista e que o coeficiente de atrito cinético é 0,20,
indique a alternativa correta.
A
D
1,0 m
B
C
2,0 m
a)
b)
c)
d)
O menino irá parar no ponto médio da parte plana BC.
Na primeira descida, o menino consegue atingir o ponto D.
O menino irá parar no ponto C, no final da parte plana da pista.
A energia mecânica dissipada até que o conjunto pare é maior que
a energia potencial que o sistema possuía no ponto de partida.
e) O menino irá parar no ponto B, no início da parte plana da pista.
Fat
(I) Teorema da Energia Cinética:
τtotal = τF – τP + τF
at
τtotal = (área) – P h – τF
at
(5 + 3) 25
τtotal =
– 10 · 4 – 10
2
τtotal = 50 J
(II) P = m g ⇒ 10 = m 10 ⇒
2
A
m = 1 kg
2
0
m V m V
–
2
2
1 V2A 1 · 0
50 =
–
2
2
τtotal =
Resolução:
Teorema da Energia Cinética:
τtotal = ΔEC
τP + τF = 0
Da qual:
m g h – µC m g D = 0
Do qual: D = h
µC
1,0
D=
(m) ⇒ D = 5,0 m
0,20
O menino percorre um total de 5,0 m na região de atrito:
2,0 m de B para C, 2,0 m de C para B e 1,0 m de B para M (ponto médio
da parte plana BC).
71 Uma partícula de massa m = 10 kg acha-se em repouso na origem
do eixo Ox, quando passa a agir sobre ela uma força resultante F ,
paralela ao eixo. De x = 0 a x = 4,0 m, a intensidade de F é constante,
de modo que F = 120 N. De x = 4,0 m em diante, F adquire intensidade
que obedece à função:
VA = 10 m/s
Resposta: d
at
Resposta: a
F = 360 – 60x (SI)
a) Trace o gráfico da intensidade de F em função de x.
b) Determine a velocidade escalar da partícula no ponto de abscissa
x = 7,0 m.
246
PARTE II – DINÂMICA
Resolução:
a)
(II) Cálculo do trabalho de F2:
τF = 8,0 (–20) ⇒ τF = –160 J
2
F (N)
2
τtotal = τF + τF = 300 – 160 ⇒
120
1
4,0
6,0
τtotal = EC – EC ⇒ 140 =
x (m)
–60
8
2,8 v2máx
⇒
2
vmáx = 10 m/s
73 (UFPR) Uma bomba de potência teórica 2,0 cv é usada para retirar água de um poço de 15 m de profundidade, a fim de encher um
reservatório de 500 ᐉ. Supondo desprezível a velocidade da água no
ponto mais alto da sua trajetória, calcule em quanto tempo o reservatório estará cheio.
Dados: 1,0 cv = 735 W; g = 9,8 m/s2; densidade da água = 1,0 kg/艎.
(6,0 + 4,0) 120 1,0 (–60)
+
(J)
2
2
Donde: τ]70 = 570 J
(II) Cálculo da velocidade:
Teorema da Energia Cinética:
10 v27
τ]70 = EC – EC ⇒ 570 =
⇒
7
0
2
Respostas: a)
0
Resposta: 10 m/s
b) (I) Cálculo do trabalho:
τ]70 = “área”
τ]70 =
τtotal = 140 J
(III) Cálculo da velocidade:
7,0
0
2
Resolução:
m g h
m g h
Pot = τ =
⇒ Δt =
Δt
Potm
Δt
v7 ⯝ 10,7 m/s
Δt =
F (N)
500 · 9,8 · 15
(s) ⇒
2,0 · 735
Δt = 50 s
120
Resposta: 50 s
7,0
0
4,0
74 (UnB-DF) Um automóvel de massa m é acelerado uniformemen-
x (m)
6,0
–60
b) ⯝ 10,7 m/s
72 O bloco da figura tem 2,8 kg de massa e parte do repouso, na
origem do eixo 0x. Sobre ele, agem exclusivamente as forças F1 e F2
representadas, cujos valores algébricos variam em função de x, conforme o gráfico a seguir:
F1
F2
x
0
te pelo seu motor. Sabe-se que ele parte do repouso e atinge a velocidade v0 em t0 segundos. Então, a potência que o motor desenvolve
após transcorridos t segundos da partida é:
m v20 2
m v2
m v20
2m v20
a)
t.
b) 2 0 t.
c)
t 0.
d)
t.
3
2
2 t0
t0
t
t20
Resolução:
v
(I) 2a Lei de Newton: F = m a ⇒ F = m 0
t0
v v
(II) Pot = F v ⇒ Pot = m 0 0 t
t0 t0
Da qual:
Pot =
m v20
t
t20
F (N)
Resposta: b
40
(F1)
75 (Mack-SP) O motor da figura leva o bloco de 10 kg da posição
20
0
2,0
4,0
6,0
8,0
10 x (m)
A para a posição B, com velocidade constante, em 10 s. O coeficiente de atrito cinético entre o bloco e o plano inclinado é 0,50. Adote
g = 10 m/s2.
– 20
(F2)
2,0
Sabendo que F1 e F2 são suprimidas na posição x = 10 m, determine a
máxima velocidade escalar atingida pelo bloco.
Resolução:
A máxima velocidade é atingida em x = 8,0 m (força resultante nula).
(I) Cálculo do trabalho de F1:
τF = 6,0 · 40 +
1
(40 + 20) 2,0
⇒
2
τF = 300 J
1
m
B
α
A
cos α = 0,80; sen α = 0,60
Qual a potência útil do motor nesse deslocamento?
Motor
Tópico 6 – Trabalho e potência
Resolução:
Pot = F v
1o caso: P = (µ m g cos θ + m g sen θ) v
2o caso: Q = µ m g v
Dividindo (I) por (II), temos:
Resolução:
Pot = F v = (Fat + Pt) v
Pot = (µ m g cos α + m g sen α) Δs
Δt
2,0
Pot = (0,50 · 10 · 10 · 0,80 + 10 · 10 · 0,60) ·
(W)
10
Pot = 20 W
µ P = µ Q cos θ + Q sen θ
76 (Fuvest-SP) Nos manuais de automóveis, a caracterização dos
motores é feita em cv (cavalo-vapor). Essa unidade, proposta no tempo das primeiras máquinas a vapor, correspondia à capacidade de um
cavalo típico, que conseguia erguer, na vertical, com auxílio de uma
roldana, um bloco de 75 kg, com velocidade de módulo 1,0 m/s.
100
m
10 m
µ (P – Q cos θ) = Q sen θ ⇒
µ=
Q sen θ
P – Q cos θ
Resposta: e
78 (Fuvest-SP) Um carro de corrida, com massa total m = 800 kg,
parte do repouso e, com aceleração constante, atinge, após 15 segundos, a velocidade de 270 km/h (ou seja, 75 m/s). A figura representa o
velocímetro, que indica a velocidade instantânea do carro. Despreze as
perdas por atrito e as energias cinéticas de rotação (como a das rodas
do carro). Suponha que o movimento ocorre numa trajetória retilínea
e horizontal.
180
θ
120
60
Para subir uma ladeira com aclive de 10%, como a da figura, um carro
de 1 000 kg, mantendo uma velocidade constante de módulo 15 m/s
(54 km/h), desenvolve uma potência útil que, em cv, é, aproximadamente, de:
(Adote g=10 m/s2.)
a) 20.
b) 40.
c) 50.
d) 100.
e) 150.
Resolução:
(I) A potência de 1 cv é dada em W por:
Pot = F v ⇒ Pot = m g v
Pot = 75 · 10 · 1,0 (W) ⇒ Pot = 750 W
(II) A potência útil desenvolvida pelo carro é calculada a seguir:
Potcarro = (F v)carro = m g sen θ vcarro
Potcarro = 1 000 · 10 · 10 · 15 (W)
100
Potcarro = 15 000 W = 15 000 (cv)
750
Potcarro = 20 cv
Resposta: a
77 (ITA-SP) Um bloco maciço requer uma potência P para ser em-
purrado, com velocidade constante, para subir uma rampa inclinada
de um ângulo θ em relação à horizontal. O mesmo bloco requer uma
potência Q quando empurrado com a mesma velocidade, em uma região plana de mesmo coeficiente de atrito. Supondo que a única fonte
de dissipação seja o atrito entre o bloco e a superfície, conclui-se que o
coeficiente de atrito entre o bloco e a superfície é:
Q
.
P
Q
.
b)
P–Q
(I)
(II)
P = m g (µ cos θ + sen θ) v
µ m g v
Q
Resposta: 20 W
a)
247
Q sen .
P–Q
Q
d)
.
P – Q cos c)
e)
Q sen .
P – Q cos 240
ω
0
300
360
km/h
a) Qual a velocidade angular ω do ponteiro do velocímetro durante a
aceleração do carro? Indique a unidade usada.
b) Qual o valor do módulo da aceleração do carro nesses 15 segundos?
c) Qual o valor da componente horizontal da força que a pista aplica
ao carro durante sua aceleração?
d) Qual a potência fornecida pelo motor quando o carro está a
180 km/h?
Resolução:
a)
360 km/h → π rad
270 km/h → Δϕ
ω=
Δϕ = 3 π rad
4
3
Δϕ 4 π
=
(rad/s) ⇒
Δt
15
ω = π rad/s
20
Nota:
Se a aceleração do carro é constante, ϕ é diretamente proporcional
a t e ω é constante.
b) α = Δv = 75 m/s ⇒ α = 5,0 m/s2
15 s
Δt
c) 2a Lei de Newton: F = m · a = m · α
F = 800 · 5,0 (N) ⇒
F = 4,0 kN
d) Pot = F · v ⇒ Pot = 4,0 · 180 (kW)
3,6
Pot = 200 kW = 2,0 · 105 W
Respostas: a) π rad/s; b) 5,0 m/s2; c) 4,0 kN; d) 2,0 · 105 W
20
248
PARTE II – DINÂMICA
79 Considere dois recipientes cilíndricos (1) e (2) feitos de mate-
rial de espessura e peso desprezíveis. Os recipientes têm raios R1 = r e
R2 = 2r e estão apoiados sobre duas prateleiras desniveladas por 1,0 m.
O recipiente (2), inicialmente vazio, está na prateleira superior, enquanto o recipiente (1), que contém 2,0 艎 de água até a altura de
40 cm em relação à parede do fundo, está apoiado na prateleira inferior. Um garoto pega o recipiente (1), ergue-o e despeja seu conteúdo
no recipiente (2).
Considerando g = 10 m/s2 e a densidade da água igual a 1,0 kg/艎, calcule o trabalho motor realizado sobre a água no transporte do recipiente
(1) para o recipiente (2).
Resolução:
Resolução:
a) MUV: v = v0 + a t
Como, em t0 = 0, EC = 0, temos v0 = 0. Logo:
0
v=a t
EC = m v2 ⇒ EC = m (a · t)2
2
2
Sendo m = 2,0 kg e observando que, em t = 4,0 s, EC = 36 J, vem:
36 =
2,0 2
a (4,0)2 ⇒
2
a = 1,5 m/s2
2a Lei de Newton:
F = m a ⇒ F = 2,0 · 1,5 (N)
F = 3,0 N
b) Teorema da Energia Cinética:
τ = EC – EC ⇒ F d = EC – EC
(2)
f
h2
CM2
5 cm
i
f
3,0 d = 36 – 9,0 ⇒
i
d = 9,0 m
Respostas: a) 3,0 N; b) 9,0 m
80 cm
Recipiente (1):
V = π r2 40
(1)
Recipiente (2):
V = π (2 r2) h2
81 Considere uma partícula de massa igual a 8,0 kg inicialmente
em repouso num ponto A de um plano horizontal. A partir do instante
t1 = 1,0 s, essa partícula é deslocada até um ponto B do mesmo plano,
sob a ação de uma força resultante F , lá chegando no instante t2 = 3,0 s.
Nos gráficos a seguir, estão registradas as variações das coordenadas
de posição x e y da partícula em função do tempo. Os trechos curvos
são arcos de parábola.
CM1
20 cm
x (m)
10,0
Como os volumes de água nos recipientes (1) e (2) são iguais, temos:
8,0
6,0
π 4 r2 h2 = π r2 40 ⇒
4,0
h2 = 10 cm
2,0
τ = m g ΔhCM ⇒ τ = 2,0 · 10 · 0,85 (J) ⇒
τ = 17 J
0
1,0
2,0
3,0
t (s)
1,0
2,0
3,0
t (s)
Resposta: 17 J
y (m)
80 Uma partícula de massa igual a 2,0 kg está em movimento reti-
líneo uniformemente acelerado sob a ação de uma força resultante F .
A energia cinética da partícula é dada em função do tempo pelo gráfico abaixo:
10,0
8,0
6,0
Ec (J)
4,0
36
2,0
0
9,0
0
2,0
4,0 t (s)
a) Qual a intensidade da força F ?
b) Qual o deslocamento da partícula no intervalo de 2,0 s a 4,0 s?
Pede-se:
a) esboçar, num diagrama yx, o deslocamento vetorial da partícula de
A até B, destacando o seu módulo;
b) calcular o trabalho da força F de A até B, bem como a intensidade
dessa força.
Tópico 6 – Trabalho e potência
Resolução:
y (m)
8,0
d
2,0
0
2,0
10
x (m)
|d | = (8,0) + (6,0) ⇒
2
2
82 Um dublê deverá gravar uma cena de um filme de ação na qual
tiros serão disparados contra ele, que estará mergulhando nas águas
de um lago profundo, descrevendo uma trajetória horizontal. Os projéteis serão expelidos com velocidade de intensidade V0 e realizarão
movimentos verticais a partir de uma altura H em relação à superfície
líquida. No local, a aceleração da gravidade tem módulo g e a influência do ar é desprezível. Admitindo-se que dentro d’água a força total de
resistência que cada projétil recebe durante a penetração tem intensidade constante e igual ao triplo do seu peso, determine, em função de
H, V0 e g , a profundidade segura p em que o dublê deverá se deslocar
para não ser atingido por nenhum projétil.
Resolução:
Teorema de Pitágoras:
2
249
(VA = V0 )
A
|d | = 10 m
b) No intervalo de 1,0 s a 3,0 s, a partícula realiza MUV nas direções 0x
e 0y.
a
a
Δx = X t2 ⇒ 8,0 = X (2,0)2 ⇒ aX = 4,0 m/s2
2
2
vx = v0 + ax t ⇒ vX = 4,0 · 2,0 (m/s)
x
vx = 8,0 m/s
a
a
Δy = y t2 ⇒ 6,0 = y (2,0)2 ⇒ ay = 3,0 m/s2
2
2
vy = v0 + ay t ⇒ vY = 3,0 · 2,0 (m/s)
y
vy = 6,0 m/s
Teorema de Pitágoras:
m
g
H
(VC = 0)
h
C
Teorema da Energia Cinética:
m v2C m v2A
–
2
2
m v20
+ τF = 0 –
2
C
τtotal =
τP
V
Vy
A→C
B→C
m g (H + h) – 3 m g h = –
g H+g h–3 g h=–
Vx
–2 g h = –
v2 = v2x + v2y
v2 = (8,0)2 + (6,0)2
Donde:
2
2
m v0
8,0 (10)2
τ=m v –
⇒ τ=
(J) ⇒
2
2
2
τ = 4,0 · 102 J
τ = F d cos 0° ⇒ 4,0 · 102 = F 10 · 1 ⇒
F = 40 N
Respostas: a) y (m)
8,0
d
2,0
2,0
10
| d | = 10 m
b) 4,0 · 102 J e 40 N
v20 H
+
4 g 2
A profundidade de segurança é p, tal que:
Teorema da Energia Cinética:
0
v20
2
v20
–g H
2
h=
v = 10 m/s
m v20
2
x (m)
ph ⇒
p
Resposta: p v20 H
+
4 g 2
v20 H
+
4 g 2
83 Um balde de massa igual a 800 g contendo inicialmente 20 litros
de água (densidade absoluta 1,0 kg/艎) é içado verticalmente a partir
do solo até uma altura de 5,0 m. A operação é realizada em 20 s, com
velocidade constante, num local em que g = 10m/s2, utilizando-se
uma corda leve e inextensível que passa por uma polia fixa ideal. O
balde, entretanto, tem uma rachadura que o faz perder água à razão de
0,08 艎/s, que pode ser considerada constante ao longo do trajeto. Desprezando-se a influência do ar, determine:
a) o trabalho motor realizado sobre o balde nesse processo;
b) a potência da força de tração aplicada pela corda sobre o balde no
fim dos primeiros 10 s.
250
PARTE II – DINÂMICA
Resolução:
84 Um carro sobe uma rampa inclinada de 30°, com velocidade
constante de intensidade v. Nessas condições, a força de resistência
do ar tem intensidade igual a um quarto do peso do carro. Em seguida, ele desce a mesma rampa com velocidade constante de intensidade 2v. Sabendo que a força de resistência do ar tem intensidade
proporcional ao quadrado da velocidade do carro, responda: qual a
razão entre as potências úteis desenvolvidas pelo motor na subida e
na descida?
F
V
v
2v
H = 5,0 M
P
30°
(I) A massa de água remanescente no balde é dada em função do tempo por:
mA = m0 – Zt
mA = 20 – 0,08 t
30°
Resolução:
(I) Subida:
F
v
(SI)
Fr
(II) O peso do conjunto balde-água tem intensidade decrescente em
função do tempo, conforme a expressão:
P = (mA + mB) g ⇒ P = (20 – 0,08t + 0,8) 10
Pt
30°
Donde: P = 208 – 0,8 t (SI)
F = Fr + P sen 30°
F= P + P ⇒ F= 3 P
4
4 2
h 20
h
(III) MRU: F = P e t = V = H = 5,0 h
T
Donde: t = 4,0 h
Pot = 3 P v
4
Pot = F v ⇒
Assim: F = 208 – 0,8 · 4,0 h
F = 208 – 3,2 h (SI)
(II) Descida:
(IV) Gráfico F = f(h):
F‘r
F (n)
2v
208
F‘
192
Pt
30°
0
a) τ(F ) = “área” ⇒ τ(F ) =
5,0 h (m)
(208 + 192) 5,0
(J)
2
τ(F ) = 1 000 J = 1,0 kJ
b) Em t = 10 s:
P = 208 –0,8 ·10 (N) ⇒ P= 200 N
Logo:
F = P = 200 N
Pot = F V cos θ
(θ = 0° e cos θ = 1)
Pot = F · H ⇒ Pot = 200 · 5,0 (W)
T
20
F’r = 4 Fr = 4 P = P
4
F’ = F’r – P sen 30°
F’ = P – P ⇒ F’ = P
2
2
Pot’ = F’ 2 v ⇒ Pot’ = P 2 v
2
Pot’ = P v
Pot =
Pot’
3 P v
4
P v
Pot = 50 W
Respostas: a) 1,0 kJ; b) 50 W
Resposta: 3
4
⇒
Pot = 3
Pot’ 4
Tópico 6 – Trabalho e potência
85 E.R. O rendimento de determinada máquina é de 80%. Saben-
do que ela recebe uma potência de 10,0 kW, calcule:
a) a potência útil oferecida;
b) a potência dissipada.
Resolução:
a) O rendimento () da máquina pode ser expresso por:
Potu
= Pot
r
Sendo = 80% = 0,80 e Potr = 10,0 kW, calculemos Potu:
Potu = Potr ⇒ Potu = 0,80 · 10,0 kW
Potu = 8,0 kW
b) Temos:
Potu = Potr – Potd
ou
Potd = Potr – Potu
Logo:
Potd = 10,0 kW – 8,0 kW
Potd = 2,0 kW
88 Os trólebus são veículos elétricos ainda em operação no transporte público urbano de algumas capitais brasileiras, como São Paulo. Para se movimentarem, eles devem ser conectados a uma linha
de força suspensa que os alimenta energeticamente, permitindo um
deslocamento silencioso com produção de níveis praticamente nulos
de poluição. Embora sua concepção tecnológica seja antiga, os trólebus funcionam com rendimentos maiores que os dos ônibus similares
movidos a diesel, sendo, porém, cativos dos trajetos pré-estabelecidos
em que existem as linhas de alimentação. Considere um trólebus trafegando com velocidade de intensidade constante, 36 km/h, num trecho
retilíneo e horizontal de uma avenida. Sabendo que a potência elétrica
que ele recebe da rede é de 5 000 kW e que seu rendimento é igual a
60%, determine:
a) a potência dissipada nos mecanismos do trólebus;
b) a intensidade da força resistente ao movimento do veículo.
Resolução:
Potu
Potu
a) (I) η =
⇒ 0,60 =
⇒ Potu = 3 000 kW
5 000
Potr
(II) Potu = Potr – Potd ou Potd = Potr = Potu
Potd = 5 000 – 3 000 (kW)
Potd = 2 000 kW
b) Potu = Fm v cos θ (θ = 0° e cos θ = 1)
3 000 · 103 = Fm 36 ⇒ Fm = 300 kW
3,6
MRU: Fr = Fm ⇒
86 Qual o rendimento de uma máquina que, ao receber 200 W, dissipa 50 W?
a) 25%
d) 100%
b) 50%
e) 150%
c) 75%
Resolução:
(I) Potu = Potr – Potd
Potu = 200 – 50 (W) ⇒
Fr = 300 kN
Respostas: a) 2 000 kW; b) 300 kN
89 Na situação da f igura a seguir, o motor elétrico faz com que
o bloco de massa 30 kg suba com velocidade constante de 1,0 m/s.
O cabo que sustenta o bloco é ideal, a resistência do ar é desprezível e adota-se |g | = 10 m/s2. Considerando que nessa operação
o motor apresenta rendimento de 60%, calcule a potência por ele
dissipada.
Potu = 150 W
Motor
Potu
(II) η =
⇒ η = 150
200
Potr
ω
g
η = 0,75 = 75%
Resposta: c
87 O rendimento de um motor é de 90%. Sabendo que ele oferece
ao usuário uma potência de 36 HP, calcule:
a) a potência total que o motor recebe para operar;
b) a potência que ele dissipa durante a operação.
Resolução:
Potu
⇒ 0,90 = 36 ⇒
a) η =
Potr
Potr
Potr = 40 HP
b) Potu = Potr – Potd ou Potd = Potr – Potu
Potd = 40 – 36 (HP)
Potd = 4 HP
Respostas: a) 40 HP; b) 4 HP
251
Resolução:
(I) MRU:
F = P ⇒ F = m g ⇒ F = 30 · 10 (N) ⇒ F = 300 N
Potu
300 · 1,0
(II) η =
⇒ η = F v ⇒ 0,60 =
Potr
Potr
Potr
Donde:
Potr = 500 W
(III) Potu = Potr – Potd ou Potd = Potr – Potu
Potd = 500 – 300 (W)
Potd = 200 W = 2,0 · 102 W
Resposta: 2,0 · 102 W
252
PARTE II – DINÂMICA
90 O esquema seguinte representa os principais elementos de um
sistema rudimentar de geração de energia elétrica. A água que sai do
tubo com velocidade praticamente nula faz girar a roda, que, por sua
vez, aciona um gerador. O rendimento do sistema é de 80% e a potência elétrica que o gerador oferece em seus terminais é de 4,0 kW.
Tubo
Velocidade
desprezível
Sendo dadas a densidade da água (1,0 g/cm3) e a aceleração da gravidade (10 m/s2), aponte a alternativa que traz o valor correto da vazão
da água.
d) 0,25 m3/s
a) 0,025 m3/s
b) 0,050 m3/s
e) 0,50 m3/s
c) 0,10 m3/s
Resolução:
(I) η =
Roda-d’água
2,0 m
Potu
4,0
⇒ 0,80 =
Potr
Potr
Potr = 5,0 kW = 5,0 · 103 W
(II) Potr = µ Z g h
5,0 · 103 = 1,0 · 103 Z 10 · 2,0
Z = 0,25 m3/s
Resposta: d
Vista lateral
2,0 m
Gerador
Vista frontal