9. (Pucpr 2004) Um ônibus percorre em 30 minutos as

1. (Ufrgs 2014) Um móvel percorre uma trajetória fechada, representada na figura abaixo, no
sentido anti-horário.
Ao passar pela posição P, o móvel está freando. Assinale a alternativa que melhor indica,
nessa posição, a orientação do vetor aceleração total do móvel.
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
2. (Ufrgs 2012) A figura a seguir apresenta, em dois instantes, as velocidades v1 e v2 de um
automóvel que, em um plano horizontal, se desloca numa pista circular.
Com base nos dados da figura, e sabendo-se que os módulos dessas velocidades são tais que
v1>v2 é correto afirmar que
a) a componente centrípeta da aceleração é diferente de zero.
b) a componente tangencial da aceleração apresenta a mesma direção e o mesmo sentido da
velocidade.
c) o movimento do automóvel é circular uniforme.
d) o movimento do automóvel é uniformemente acelerado.
e) os vetores velocidade e aceleração são perpendiculares entre si.
3. (Uesc 2011) Considere um móvel que percorre a metade de uma pista circular de raio igual
a 10,0m em 10,0s. Adotando-se
como sendo 1,4 e
igual a 3, é correto afirmar:
a) O espaço percorrido pelo móvel é igual a 60,0m.
b) O deslocamento vetorial do móvel tem módulo igual a 10,0m.
c) A velocidade vetorial média do móvel tem módulo igual a 2,0m/s.
d) O módulo da velocidade escalar média do móvel é igual a 1,5m/s.
e) A velocidade vetorial média e a velocidade escalar média do móvel têm a mesma
intensidade.
4. (Pucrj 2010) Um pequeno avião acelera, logo após a sua decolagem, em linha reta,
formando um ângulo de 45o com o plano horizontal.
Sabendo que a componente horizontal de sua aceleração é de 6,0 m/s2, calcule a componente
vertical da mesma.
(Considere g = 10 m/s2)
a) 6,0 m/s2
b) 4,0 m/s2
c) 16,0 m/s2
d) 12,0 m/s2
e) 3,0 m/s2
5. (Ufla 2010) Um engenheiro projeta a curva de uma estrada e após estudos minuciosos
conclui que a velocidade de segurança (vs) nessa curva deve respeitar a expressão: vs =
, em que R é o raio da curva.
Segundo o engenheiro, um veículo transitando nessa curva pode ficar sob ação de uma
aceleração centrípeta máxima de:
a) 10 m/s2
b) 5 m/s2
c) 25 m/s2
d) 20 m/s2
6. (Ufpb 2007) Considere os vetores A, B e F, nos diagramas numerados de I a IV.
Os diagramas que, corretamente, representam a relação vetorial F = A - B são apenas:
a) I e III
b) II e IV
c) II e III
d) III e IV
e) I e IV
7. (G1 - cftce 2007) Dados os vetores "a", "b", "c", "d" e "e" a seguir representados, obtenha o
módulo do vetor soma: R = a + b + c + d + e
a) zero
b)
c) 1
d) 2
e)
8. (Ufal 2007) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se
caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à
primeira. A distância em linha reta, da caverna ao lago era, em metros,
a) 680
b) 600
c) 540
d) 520
e) 500
9. (Pucpr 2004) Um ônibus percorre em 30 minutos as ruas de um bairro, de A até B, como
mostra a figura:
Considerando a distância entre duas ruas paralelas consecutivas igual a 100 m, analise as
afirmações:
I. A velocidade vetorial média nesse percurso tem módulo 1 km/h.
II. O ônibus percorre 1500 m entre os pontos A e B.
III. O módulo do vetor deslocamento é 500 m.
IV. A velocidade vetorial média do ônibus entre A e B tem módulo 3 km/h.
Estão corretas:
a) I e III.
b) I e IV.
c) III e IV.
d) I e II.
e) II e III.
10. (G1 - cftce 2004) Uma partícula desloca-se sobre a trajetória formada pelas setas que
possuem o mesmo comprimento L. A razão entre a velocidade escalar média e a velocidade
vetorial média é:
a)
b)
c) 1
d)
e) 2
11. (Ufc 2003) A figura adiante mostra o mapa de uma cidade em que as ruas retilíneas se
cruzam perpendicularmente e cada quarteirão mede 100 m. Você caminha pelas ruas a partir
de sua casa, na esquina A, até a casa de sua avó, na esquina B. Dali segue até sua escola,
situada na esquina C. A menor distância que você caminha e a distância em linha reta entre
sua casa e a escola são, respectivamente:
a) 1800 m e 1400 m.
b) 1600 m e 1200 m.
c) 1400 m e 1000 m.
d) 1200 m e 800 m.
e) 1000 m e 600 m.
12. (Unifesp 2002) Na figura, são dados os vetores
,
e
.
Sendo u a unidade de medida do módulo desses vetores, pode-se afirmar que o vetor
+
=
-
tem módulo
a) 2u, e sua orientação é vertical, para cima.
b) 2u, e sua orientação é vertical, para baixo.
c) 4u, e sua orientação é horizontal, para a direita.
d) (
)u, e sua orientação forma 45° com a horizontal, no sentido horário.
e) (
)u, e sua orientação forma 45° com a horizontal, no sentido anti-horário.
13. (Ufc) Na figura a seguir, onde o reticulado forma quadrados de lados ℓ=0,5cm, estão
desenhados 10 vetores contidos no plano xy. O módulo da soma de todos esses vetores é, em
centímetros:
a) 0,0.
b) 0,5.
c) 1,0.
d) 1,5.
e) 2,0.
14. (Mackenzie) Com seis vetores de módulo iguais a 8u, construiu-se o hexágono regular a
seguir. O módulo do vetor resultante desses 6 vetores é:
a) 40 u
b) 32 u
c) 24 u
d) 16 u
e) zero
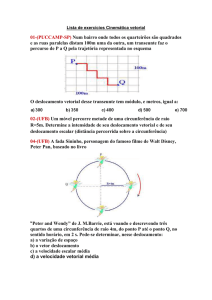
15. (Puccamp) Num bairro, onde todos os quarteirões são quadrados e as ruas paralelas
distam 100 m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada
no esquema a seguir.
O deslocamento vetorial desse transeunte tem módulo, em metros, igual a
a) 300
b) 350
c) 400
d) 500
e) 700
16. (Uel) Dois vetores perpendiculares
1
e
respectivamente. Os módulos, em newtons, de
a) 20 e 20
2
representam forças de 12 N e 16 N,
1-
2
e
1+
2
são, respectivamente,
b) 12
e 16
c) 11 e 40
d) 4
e 28
e) 4 e 28
17. (Fei) Uma automóvel realiza uma curva de raio 20 m com velocidade constante de 72
km/h. Qual é a sua aceleração durante a curva?
a) 0 m/s2
b) 5 m/s2
c) 10 m/s2
d) 20 m/s2
e) 3,6 m/s2
18. (Uece) A figura a seguir mostra a trajetória da bola lançada pelo goleiro Dida, no tiro de
meta. Desprezando o efeito do ar, um estudante afirmou:
I. A aceleração vetorial da bola é constante.
II. A componente horizontal da velocidade da bola é constante.
III. A velocidade da bola no ponto mais alto de sua trajetória é nula.
Destas afirmativas, é(são) correta(s) somente:
a) I
b) II
c) I e II
d) II e III
19. (Unicamp) A figura a seguir representa um mapa da cidade de Vectoria o qual indica a
direção das mãos do tráfego. Devido ao congestionamento, os veículos trafegam com a
velocidade média de 18 km/h. Cada quadra desta cidade mede 200 m por 200 m (do centro de
uma rua ao centro de outra rua). Uma ambulância localizada em A precisa pegar um doente
localizado bem no meio da quadra em B, sem andar na contramão.
a) Qual o menor tempo gasto (em minutos) no percurso de A para B?
b) Qual é o módulo do vetor velocidade média (em km/h) entre os pontos A e B?
20. (Fatec) Dados os vetores A, B e C, representados na figura em que cada quadrícula
apresenta lado correspondente a uma unidade de medida, é correto afirmar que a resultante
dos vetores tem módulo:
a) 1
b) 2
c) 3
d) 4
e) 6
21. (Ufpe) Uma pessoa atravessa uma piscina de 4,0 m de largura, nadando com uma
velocidade de módulo 4,0 m/s em uma direção que faz um ângulo de 60° com a normal.
Quantos décimos de segundos levará o nadador para alcançar a outra margem?
22. (G1) Observe a figura a seguir e determine quais as flechas que:
a) tem a mesma direção.
b) tem o mesmo sentido.
c) tem o mesmo comprimento.
d) são iguais.
23. (G1) Determine o vetor soma (resultante) entre dois vetores perpendiculares (angulo reto)
de módulos 6 N e 8 N:
24. (Unitau) Um avião sai de um mergulho percorrendo um arco de circunferência de 300 m.
Sabendo-se que sua aceleração centrípeta no ponto mais a baixo do arco vale 8,33 m/s2,
conclui-se que sua velocidade, nesse ponto, é:
a) 8,33 m/s
na direção horizontal.
b) 1,80 × 102 km/h na direção horizontal.
c) 1,80 × 102 km/h na direção vertical.
d) 2,50 × 103 m/s na direção horizontal.
e) 2,50 × 103 m/s na direção vertical.
25. (Unesp) A escada rolante que liga a plataforma de uma estação subterrânea de metrô ao
nível da rua move-se com velocidade constante de 0,80 m/s.
a) Sabendo-se que a escada tem uma inclinação de 30° em relação à horizontal, determine,
com o auxílio da tabela adiante, a componente vertical de sua velocidade.
b) Sabendo-se que o tempo necessário para que um passageiro seja transportado pela
escada, do nível da plataforma ao nível da rua, é de 30 segundos, determine a que
profundidade se encontra o nível da plataforma em relação ao nível da rua.
26. (Uel) Considere a figura a seguir.
Dadas as forças
a) 30
b) 40
c) 50
d) 70
e) 80
, o módulo de sua resultante, em N, é
TEXTO PARA A PRÓXIMA QUESTÃO:
Uma esfera de massa m, suspensa por um fio a um ponto O, é solta, a partir do repouso, de um ponto A,
descrevendo um arco de circunferência e passando a oscilar entre as posições extremas A e E. A figura a
seguir ilustra esse movimento.
27. (Cesgranrio)
Com base nas opções apresentadas na figura anterior, o vetor que representa a aceleração da
esfera, ao passar pelo ponto D, é:
a) I
b) II
c) III
d) IV
e) V
Gabarito:
Resposta da questão 1:
[D]
O movimento é curvilíneo retardado. Portanto, a componente tangencial da aceleração
tem sentido oposto ao da velocidade a componente centrípeta
figura ilustra a situação.
dirigida para o centro. A
Resposta da questão 2:
[A]
Todo movimento circular contém uma componente centrípeta voltada para o centro da
circunferência de módulo não nulo.
Resposta da questão 3:
[C]
A figura mostra os deslocamentos escalar e vetorial em meia volta.
→
→
Resposta da questão 4:
[A]
Como se pode observar na figura a seguir, se a aceleração é inclinada de 45°, as suas
componentes vertical e horizontal têm mesma intensidade.
Portanto: ay = ax = 6 m/s2.
Ou ainda: tg 45° =
⇒ ay = 6 m/s2.
Resposta da questão 5:
[C]
ac =
⇒ ac = 25 m/s2.
Nota: o enunciado poderia ser mais preciso no segundo parágrafo, pois a máxima aceleração
que um móvel pode ter numa curva é aquela para o limite de derrapagem e não a de
segurança. Ficaria melhor assim: “Segundo o engenheiro, um veículo transitando nessa curva,
para descrevê-la com segurança, pode ficar sob ação de uma aceleração centrípeta máxima
de:”
Resposta da questão 6:
[B]
III III – igual ao I
IV Resposta da questão 7:
[E]
Resposta da questão 8:
[D]
A figura mostra os deslocamentos citados e a distância procurada.
Como o triângulo mostrado é retângulo é só aplicarmos o teorema de Pitágoras.
Resposta da questão 9:
[A]
Resposta da questão 10:
[B]
Resposta da questão 11:
[C]
Resposta da questão 12:
[B]
Resposta da questão 13:
[E]
Resposta da questão 14:
[B]
Resposta da questão 15:
[D]
Resposta da questão 16:
[A]
Resposta da questão 17:
[D]
Resposta da questão 18:
[C]
I) Correta. A aceleração é sempre a gravidade.
II) Correta. Não há aceleração horizontal
III) Errada. A velocidade no ponto mais alto é igual à componente horizontal da velocidade.
Resposta da questão 19:
a) 3 min.
b) 10,0 km/h.
Resposta da questão 20:
[A]
Resposta da questão 21:
20 ds.
Resposta da questão 22:
a) A e D; B e F; C e E
b) A e D; B e F
c) B e D
d) Nenhum par.
Resposta da questão 23:
10 N
Resposta da questão 24:
[B]
HORIZONTAL
Resposta da questão 25:
a) 0,40 m/s
b) 12 m
Resposta da questão 26:
[C]
Resposta da questão 27:
[C]