Aula Teórica - 13 - Laboratório de Química Aplicada

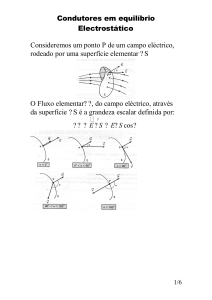
Eletricidade
Quantização da carga
 todos os objectos directamente observados na
natureza possuem cargas que são múltiplos
inteiros da carga do eletrão
a unidade de carga C, é o coulomb
A Lei de Coulomb
 A primeira constatação de que a interacção
entre cargas eléctricas obedece à lei de força
Sendo:
r - distância entre as cargas
F - o módulo da força
Esta constatação foi feita por Priestley em 1766. Priestley observou que um recipiente metálico carregado, não possui
cargas na superfície interna, não exercendo forças sobre uma carga colocada dentro dele.
A Lei de Coulomb
Medidas diretas da lei foram realizadas em
1785 por Coulomb, utilizando uma balança
de torção.
sendo
A Lei de Coulomb
O resultado obtido por Coulomb pode ser
expresso como
q1 e q2 – grandeza escalar que são ao valor o sinal das respectivas cargas
^
r12 - vector
unitário da carga 1 para a carga 2
O Campo eléctrico
Consideremos a equação
aplicada à força sentida por uma carga q0, devida
à N cargas q1 q2 … qn
onde
é a distância desde a carga
até o ponto do espaço onde se
encontra a carga
e
é o vector unitário apontando na direcção da
linha que une as cargas
e , no sentido de
para
O Campo eléctrico
 A mesma equação pode ser escrita formalmente
como:
 sendo:
 A grandeza
é denominada campo eléctrico
O campo elétrico
Para que se possa observar, ou seja, medir, o
campo eléctrico , é necessário posicionar uma
carga num determinado ponto do espaço,
medir a força sentida por esta carga e calcular
a razão
supondo uma situação idealizada, onde a carga
campo produzido pelas outras cargas
não altera o
O campo eléctrico
a interação entre duas cargas ocorre em
duas etapas:
 Primeiro a carga cria o campo ,
 em seguida, a carga interage com o campo
 Este processo é de fundamental importância em problemas dependentes do tempo,
tendo em vista que os sinais eletromagnéticos se propagam-se, no vácuo, com a
velocidade da luz
Linhas de campo
a visualização qualitativa do campo eléctrico
pode ser feita usando as chamadas linhas de
campo.
Linhas de campo
As linhas são tangentes, em cada ponto, à
direcção do campo eléctrico neste ponto.
A intensidade do campo é proporcional ao
número de linhas por unidade de área de uma
superfície perpendicular às linhas.
Linhas de campo
Linhas de campo de uma carga puntiforme positiva e de uma carga
punctiforme negativa.
Linhas de campo
Linhas do campo de um dipolo
Linhas de campo
Fluxo do campo eléctrico
 Campo uniforme
área A
atravessando uma superfície ortogonal de
 Campo uniforme atravessando uma superfície, cuja normal
forma um ângulo com a direcção do campo
Lei de Gauss
Q
E
.
dS
=
SF εo
 O fluxo do campo elétrico através de uma superfície fechada é
igual à carga total no interior dessa superfície dividida por ε0
 - Lei equivalente à lei de Coulomb.
 - Formulação inversa – através do conhecimento do campo
podemos conhecer a carga total.
 -Permite-nos calcular o campo em problemas com distribuições
simétricas de carga.
ε = 8.84×10−12 C2 N−1 m−2
[Q] = coulomb
Campo Eléctrico
O campo eléctrico é uma grandeza física.
Rodeia qualquer carga e estende-se até o infinito.
Q
E=k 2
r
F=qE
E=V /d
Os átomos de um material vão interferir
no movimento dos electrões e, portanto,
também participarão das propriedades
eléctricas do material.
Cargas elétricas (livres) podem movimentar-se sob a ação de
campos elétricos e magnéticos, e em diversos ambientes.
No caso de eletrões movendo-se em resistências, em regime
estacionário, sob a acção de um campo eléctrico
Deslocação
Campo eléctrico
Intensidade da corrente elétrica
Define-se intensidade de corrente elétrica
como a quantidade de cargas que atravessa a
secção recta de um condutor, por unidade de
tempo. Isto é,
q
i=
t
A corrente eléctrica por unidade de área
transversal define o módulo do vector densidade
de corrente J.
i
J=
A
Carga Elétrica


A carga elétrica é uma propriedade fundamental da matéria.
As cargas eléctricas do protão, do eletrão e do neutrão são,
respetivamente




Qp = e = 1.6*10-19 C
Qe = -e = -1.6*10-19 C
Qn = 0 C
as massas em repouso são

mp mn = 1.672*10-24g

me = 9.11*10-28

e os raios, assumindo-as esféricas, são

rp  rn re = 2.81*10-15m
Força Elétrica

A Lei de Coulomb estabelece que duas cargas
elétricas pontuais se atraem ou repelem com uma
força cuja intensidade é:
Campo Eléctrico

O campo eléctrico é uma medida da
acção que uma carga exerce sobre as
cargas eléctricas localizadas no seu raio
de acção.
E – campo eléctrico [ N/C ]
q – carga [ C ]
Densidade de corrente e velocidade de
deslocação
Supondo existirem ‘n’ electrões por unidade de volume; esta será a densidade de
portadores do material.
A densidade de cargas no condutor será ‘ne’, e a carga total no segmento
de condutor será
Dq = neAL
Um electrão percorrerá este segmento no intervalo de tempo
Dt = L/Vd
onde Vd é a velocidade de deslocamento.
Da definição de corrente, obtém-se
i = Dq/Dt = neAVd
Da definição de densidade de corrente, obtém-se
J = neVd
A corrente é o fluxo da densidade de corrente!
Corrente elétrica



Chama-se corrente eléctrica à carga eléctrica
em movimento
Para que a carga eléctrica se desloque entre
dois pontos de um condutor é necessário que
exista entre esses dois pontos uma diferença de
potencial.
Os dispositivos que provocam essa deslocação
são chamados geradores.
Efeitos da corrente eléctrica




Efeito térmico - efeito de Joule
Produção de campo magnético
Efeito químico
Efeitos fisiológicos
Geradores

Eletrolíticos

Mecânicos

Termoelétricos
Função do gerador

Para que haja corrente eléctrica num condutor, é necessário que os
iões ou eletrões fiquem sujeitos a forças.

Estas forças decorrem da existência de um campo elétrico.

Os corpos ao serem formados de um número muito grande de
partículas eletrizadas, a distribuição dessas partículas nos átomos
faz com que o campo resultante seja nulo no condutor.

Para que surja um campo no interior de um condutor, precisamos
de um dispositivo gerador.

Os iões positivos ficam sujeitos à força de mesmo sentido que o
campo; os iões negativos ficam sujeitos à força que tem sentido
oposto ao do campo . Assim, pode haver movimento de iões
positivos num sentido e de iões negativos em sentido oposto.
Tipos de condução

Condução eletrónica ou condução metálica –
condutores de 1ª classe - deslocamento de iões é
desprezável em relação ao dos eletrões

Condução eletrolítica - condutores de 2ª classe.

Condução gasosa - condutores de 3ª classe.
Diferença de potencial


Se em cada ponto A do condutor há um
campo , também há um potencial V
hipótese simplificadora: admitimos que
todos os pontos de uma mesma secção
transversal do condutor tenham o mesmo
potencial
Diferença de potencial


Admitamos que na secção S1 todos os pontos
tenham o mesmo potencial que o ponto B
A diferença de potencial entre duas secções
transversais S1 e S2 é igual à diferença de
potencial entre um ponto qualquer B de S1 e um
ponto qualquer C de S2
Diferença de potencial


É indiferente referir diferença de potencial
entre “dois pontos do condutor” ou entre
“duas secções transversais do condutor”
O trabalho realizado no deslocamento de
uma carga q do potencial VA para o
potencial VB
Intensidade de corrente
elétrica

Seja S uma secção transversal de um
condutor e
a carga elétrica que passa
por essa secção durante o um intervalo de
tempo
Intensidade de corrente
eléctrica

Se a intensidade média é constante para
qualquer valor do intervalo de tempo Dt a
carga Dq que passa por uma secção
transversal do condutor é diretamente
proporcional ao tempo (de passagem)
Intensidade de corrente
eléctrica



Neste caso chamamos simplesmente intensidade de
corrente, em vez de intensidade média da corrente.
Sendo t o tempo necessário à passagem da carga q, e i
a intensidade de corrente, temos
Ou seja, a intensidade de corrente eléctrica, constante
numa secção transversal do condutor, é numericamente
igual à carga eléctrica que passa pela secção durante a
unidade de tempo.