TEOREMA DE THEVENIN E NORTON
Teoremas aplicados para análise e
solução de circuitos.
Permite esconder informações
desnecessarias e se concentrar no
que é relevante e importante na
análise.
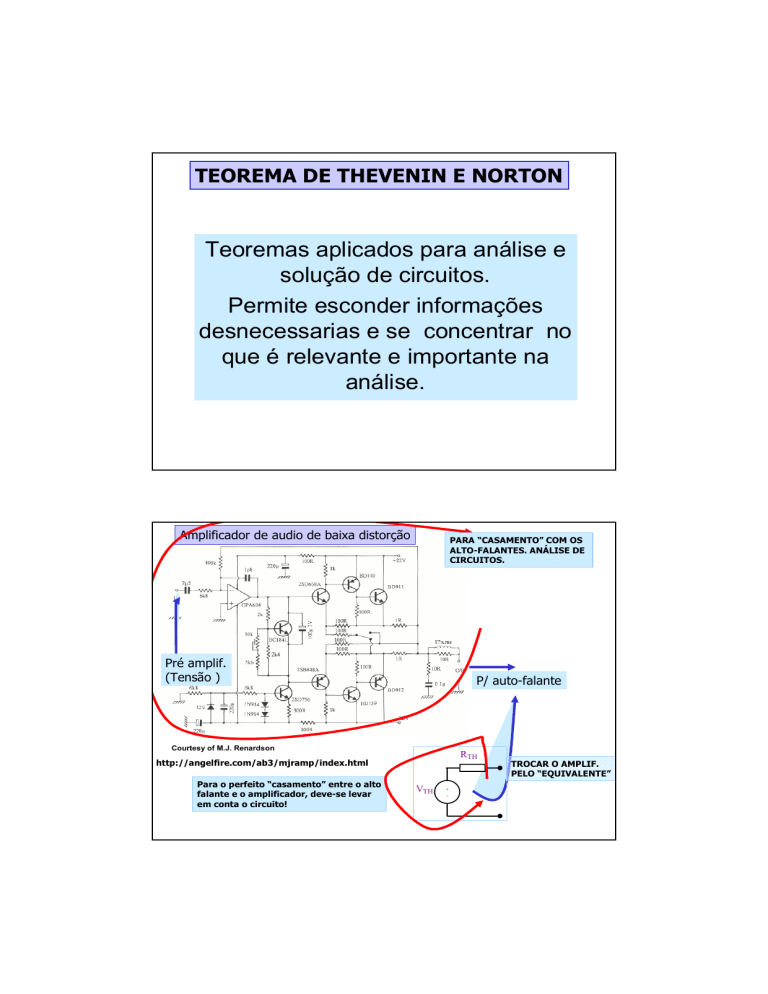
Amplificador de audio de baixa distorção
PARA “CASAMENTO” COM OS
ALTO-FALANTES. ANÁLISE DE
CIRCUITOS.
Pré amplif.
(Tensão )
P/ auto-falante
Courtesy of M.J. Renardson
RTH
http://angelfire.com/ab3/mjramp/index.html
Para o perfeito “casamento” entre o alto
falante e o amplificador, deve-se levar
em conta o circuito!
VTH
+
-
TROCAR O AMPLIF.
PELO “EQUIVALENTE”
TEOREMA “EQUIVALÊNCIA” DE THEVENIN
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
RTH
+
−
vTH
+
i
a
vO
b
_
+
i
a
LINEAR CIRCUIT
vO
_
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART B
b
PART B
PART A
Circuito equivalente de
vTH
Thevenin Equivalent Source
Thevenin para PARTE A
RTH
Thevenin Equivalent Resistance
TEOREMA “EQUIVALÊNCIA” DE THEVENIN
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
TEOREMA ‘EQUIVALÊNCIA” DE NORTON
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
+
vO
RN
b
_
+
iN
a
i
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART B
a
i
LINEAR CIRCUIT
vO
b
_
PART B
PART A
Circuito equivalente Norton
para a PARTE A
iN
RN
Thevenin Equivalent Source
Thevenin Equivalent Resistance
TEOREMA ‘EQUIVALÊNCIA” DE NORTON
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
OUTRA VISÃO DOS TEOREMAS DE THEVENIN E NORTON
i a
RTH
vOC
+
_
i
+
vO
_
i SC
RTH
−
Norton
Thevenin
iSC =
+
vO
b
vOC
RTH
Estes equivalentes podem ser vistos como transformações de fontes.
Converter uma fonte de tensão em série com um resistor para uma
fonte de corrente em paralelo com o mesmo resistor.
TRANSFORMAÇÕES DE FONTES PODEM SER INTERESSANTES PARA
REDUZIR A COMPLEXIDADE DE UM CIRCUITO
OUTRA VISÃO DOS TEOREMAS DE THEVENIN E NORTON
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
O EFEITO DO TEOREMA DE THÉVENIN
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
CIRCUITO EQUIVALENTE THÉVENIN
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
EXEMPLO:
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
SOLUÇÃO:
Resistência de
Thévenin:
RTH = R1 // R2 = 2Ω
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Tensão de Thévenin: Tensão de circuito aberto ETh
Divisor de tensão:
ETH = VOC =
6
9 = 6V
6+3
Circuito Equivalente:
IL =
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
ETh
RTh + RL
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
EXEMPLO:
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Solução:
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Resistência de Thévenin:
RTH = R1 + R2 = 6Ω
Tensão de Thévenin: Circuito aberto
ETh = V1 = I1 R1 = (12 A)(4Ω) = 48V
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Circuito Equivalente:
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
EXEMPLO (Norton):
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
SOLUÇÃO:
Resistência Norton:
RTH = R1 // R2 = 2Ω
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Corrente Norton: Curto Circuito
IN =
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
E 9V
=
= 3A
R1 3Ω
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Circuito Equivalente Norton
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Conversão Norton - Thévenin
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
EXEMPLO: RESOLVER POR TRANSFORMAÇÃO
Entre os terminais conecta-se uma fonte
de corrente e uma resistência em paralelo
O valor da fonte de corrente é dado por
12V/3k
Os resistores de 3k e 6k, em paralelos
podem ser combinados
Entre os terminais conecta-se uma fonte
de tensão em serie com o resistor
A fonte terá valor igual a 4mA*2k
Os resistores de 2k podem ser conectados
e combinados em serie
Após a transformação das fontes pode-se combiná-las
A fonte de corrente equivalente terá valuor 8V/4k
e combinada com a outra fonte de corrente, será 4mA
Opções para este ponto:
1. Nova transformação de fonte, gerando um
Circuito de uma única malha
2. Uso do divisor para obter Io e então
Calcular Vo através da Lei de Ohm
Procedimento geral para determinar o equivalente de Thevenin
vTH
Open Circuit voltage
i SC
Short Circuit Current
voltage at a - b if Part B is removed
current through a - b if Part B is replaced
RTH
by a short circuit
v
= TH
Thevenin Equivalent Resistance
i SC
1. Determinar a
Fonte Equivalente
de Thevenin
Remover part B e
Calcular a tensão
de CIRCUITO
Vab
ABERTO
Circuito da 1a parte
i =0 a
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
+
vOC
_
b
+
Vab
_
Circuito da 2a parte
Remover part B e
2. Determinar a
calcular a corrente
corrente de
CURTO CIRCUITO CURTO CIRCUITO Iab
vTH = vOC , RTH =
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
vOC
i SC
a
i SC
+
v=0
I ab
_
b
“PROVA” PARA DETERMINAÇÃO DO EQUIVALENTE DE THEVENIN
R1
VTH
a
VS
+
-
IS
R2
I SC
To Part B
Qual é a melhor técnica para calcular a
tensão de circuito aberto?
b
Agora determinar a corrente de curto circuito
através da superposição.
“Abrindo” a fonte de corrente
Quando a fonte de tensão for curto
circuitada, ou seja, tornada zero
I SC = I S +
1
ISC
=
VTH
I SC
VS
R1
2
I SC
= IS
VS
R1
Para calcular a resistência de Thevenin:
RTH =
Parte B é irrelevante.
A tensão Vab será o valor da fonte
Equivalente de Thevenin.
VTH VTH − VS
+
− IS = 0
R2
R1
(
1
1
V
+ )VTH = S + I S
R1 R2
R1
VTH =
ANÁLISE
NODAL
R2
RR
VS + 1 2 I S
R1 + R2
R1 + R2
VTH =
R1 R2 VS
+ I S
R1 + R2 R1
RTH =
R1R2
R1 + R2
Para este caso, a resistência de Thevenin pode ser calculada como
a resistência “vista” de a - b quando todas as fontes independentes
foram “zeradas”
*
5kΩ
“PARTE B”
6V
VO =
EXEMPLO
1k
(6V ) = 1[V ]
1k + 5k
OBTER Vo USANDO THEVENIN
Na região ilustrada pode-se usar transformação
de fonte (2 x) reduzindo-se a primeira parte para
fonte simples com resistores.
... Ou aplicar Equivalente de Thevenin
para toda parte (vista como “Part A”)
RTH = 4kΩ
O circuito original passa ser...
VTH =
6
12[V ] = 8[V ]
3+ 6
Para tensão de malha aberta
a parte for a da região é
eliminada.
Pode-se aplicar Thevenin uma ou mais
vezes!
+
R1TH = 4kΩ
1
VTH
−
Para tensão de malha aberta: KVL
1
TH
V
= 4k * 2mA + 8V = 16V
...e através de um simples divisor de tensão!!
V0 =
8
16[V ] = 8V
8+8
Ou somente através de Thevenin e divisor de tensão
Resistência de Thevenin
“Parte B”
Para tensão de Thevenin analisa-se o
Seguinte circuito
MÉTODO??
RTH = 8kΩ
SUPERPOSIÇÃO, por exemplo:
Contribuição da fonte de tensão
1
VOC
=
6
12V = 8V
3+ 6
Contribuição da fonte de corrente
2
VOC
= (3k // 6k + 2k) *(2mA) = 8V
Equivalente Thevenin “Parte A”
Divisor de Tensão
EXEMPLO
CALCULAR Vo USANDO DE THEVENIN
RTH = 10/3 kΩ
“Parte B”
Para tensão de circuito aberto pode-se analisar o seguinte circuito, “PARTE A”…
Loop Analysis
I 2 = 2mA
− 6V + 4kI1 + 2k ( I1 − I 2 ) = 0
6 + 2I2
5
mA = mA
6
3
= 4k * I1 + 2k * I 2 = 20 / 3 + 4V = 32 / 3[V ]
I1 =
VOC
O circuito fica...
+
USO DE THEVENIN PARA CALCULAR Vo
“PART B”
I
VOC
−
9kI = 18[V ] ⇒ I = 2mA
VOC = 3kI − 12 = −6[V ]
RESULTANDO O CIRCUITO EQUIVALENTE
RTH = 2kΩ 2kΩ
RTH
RTH = 3k || 6k = 2k
+
4kΩ
−
VTH = −6V
VO =
+
VO
−
4
(−6V ) = −3[V ]
4+4
CALCULAR Vo USANDO NORTON
4k
I
RN
2k
IN
I SC
RN = RTH = 3kΩ
PARTE B
12V
I SC = I N =
− 2mA = 2mA
3k
RN
VO = 2kI = 2k
I N
RN + 6 k
3
4
VO = 2 (2) = [V ]
9
3
CALCULAR Vo USANDO THEVENIN
VTH
PARTE B
RTH
+
+
-
VTH − 12
+ 2mA = 0
3k
RTH = 3k + 4k
2k
VO
VTH
−
VO =
2
4
(6V ) = [V ]
2+7
3
Determinar Thévenin entre a e b
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Solução: retirando a parte “B”
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Resistência Thévenin: ponto de vista dos
terminais a e b
RTh = R1 // R2 =
(6Ω)(4Ω)
= 2,4Ω
6Ω + 4 Ω
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Determinação de tensão Thévenin – Circuito aberto:
ETh =
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
R1 E1
48V
=
= 4,8V
R1 + R2
10
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Circuito Equivalente Thévenin
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
EQUIVALENTE DE THEVENIN PARA CIRCUITS COM FONTES DEPENDENTES
Não se pode iniciar um circuito contendo somente
fontes dependentes.
Como preve a variável de controle?
O que acontece se a = R + R ?
1
− aI x + ( R1 + R2 ) I X = 0
(− a + R1 + R2 )I x = 0
− a + R1 + R2 ≠ 0 ⇒ I x = 0
2
PARA QUALQUER PROJETO DE CICUITO COM SOMENTE FONTES
DEPENDENTES
VOC = 0, I SC = 0
Esta é uma simplificação!!
É necessário uma boa aproximação para calcular
a resistência equivalente de Thevenin
VTH = 0
Como não se pode iniciar o cálculo, inseri-se uma
fonte externa
A fonte pode ser escolhida entre tensão ou corrente,
bem como seu valor(escolha arbitraria!)
A escolha é direcionada em função da simplicidade
do circuito resultante (e do resultado)
ESCOLHENDO UMA TENSÃO...
CALCULAR A CORRENTE FORNECIDA PELA
FONTE ESCOLHIDA
IP = IX +
(VP )
VP − aI X
R1
IX =
VP
R2
1
1
a
VP
I P =
+ −
R2 R1 R1 R2
VP
IP
VP
=
1
1
a
+ −
VP
R2 R1 R1 R2
RTH =
(VP)
RTH
O VALOR ESCOLHIDO PARA A TENSÃO DE PROVA É IRRELEVANTE.
A MAIORIA DAS VEZES É AJUSTADO PARA “UM”.
ESCOLHENDO-SE UMA FONTE DE CORRENTE DE PROVA
Calcular a tensão no Nó, Vp
KCL
(IP )
V
IX = P
VP VP − aI X
+
− IP = 0
R2
R2
R1
1
1
a
VP = I P
+ −
R
R
R
R
2
1
1 2
(I P )
RTH =
VP
IP
O VALOR DA CORRENTE DE PROVA É IRRELEVANTE.
POR SIMPLICIDADE FOI ESCOLHIDA IGUAL A “UM”.
EXEMPLO
DETERMINE O EQUIVALENTE DE THEVENIN
KCL @V1 :
V1
VP
V1 V1 − 2V X V1 − VP
+
+
=0
1k
2k
1k
Variável de controle:
V X = VP − V1
SOLVING THE EQUATIONS
4
V1 = VP ,
7
IP =
Usar fonte de corrente ou tensão de prova?
Usando a ponta de prova de tensão há
relação entre os Nós e o conectado com a fonte.
RTH =
VP
IP
EXAMPLO
3
V X = VP
7
VP VP − 2V X V X
+
+
2k
1k
1k
IP =
15VP
14k
VP = 14 kΩ
I P 15
Usando tensão de prova simplifica
em relação a corrente de prova.
Encontrar o circuito Equivalente de Thevenin em A - B
Somente Fonte Dependente. Vth = 0
Para calcular o resistência vamos inserir
uma fonte de prova.
Opção por uma fonte de corrente
RTH =
@V_1
+
VP
−
“Convenção” circuito com fonte
dependente – uso de análise nodal
VP
IP
IP
(IP )
@V_2
Variável de controle
3(V1 − 2V1 ) + 6V1 + 2(V1 − V2 ) = 0
2(V2 − V1 ) + 3V2 = 6[V ]
RTH
A
B
Equivalente de Thevenin
5V1 − 2V2 = 0 * / 2
− 2V1 + 5V2 = 6 * / 5
V2 =
(VP = V2 ) ∩ ( I P = 1mA) ⇒ RTH =
V2
= (10 / 7)kΩ
1mA
30 10
=
21 7
PROBLEMA
RTH
A
B
Equivalente Thevenin
− VP +
I P = 1mA
I_1 = I_p/2
I_3=0
R_th = 2kOhms
MUST FIND V AB = VP . METHOD?
Análise de malha
I1 =
RTH
V
V
= P = P
I P 1mA
A resistência é
numericamente igual
a Vp mas com
unidade em KOhm
VX
; I2 = I P
2000
2k * I 3 + 1k * ( I 2 + I 3 ) + 2k * ( I 3 + I 2 − I1 ) + 4k * ( I 3 − I1 ) = 0
Variável de controle V X = 1k * ( I 3 + I 2 )
Tensão através da corrente de prova
− VP + 1k * ( I 3 + I 2 ) + 2k * ( I 3 + I 2 − I1 ) = 0
Equivalente de Thevenin
Circuitos com Fontes Dependentes e Independentes
Calcular a tensão de circuito aberto e corrente de curto circuito
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
RTH
+
-
+
i
vO
_
a
VTH
VTH = VOC
RTH =
VOC
I SC
a
b
Para cada equivalente de Thevenin
resolve-se dois circuitos
Qualquer uma das técnicas discutidas podem ser
usadas; i.e., KCL, KVL, combinação serie/paralelo,
análise de malha ou nó, superposição,
transformação de fonte, homogeneidade…
b
A aproximação de “zerar” todas as fontes e
combinar as resistências para determinar a
resistência de Thevenin em geral não se aplica!!
Obter Vo
“Parte A” deixar mais simples possível.
“Part B”
Depois “Parte A” é substituida pelo equivalente
de Thevenin tornando-se um circuito simples
As fontes dependentes e suas variáveis
de controle devem permanecer
Através do super Nó
Tensão de circuito aberto
V1
Resolvendo
Corrente de curto
VA
V1 − VOC = 12 ⇒ V1 = 12 + VOC
(12 + VOC ) − (−aI 1X ) 12 + VOC VOC
KCL no super Nó
+
+
=0
1k
2k
VOC 2k
1
IX =
Equação variável de controle
2k
36
I "X
VOC = −
4 + (a / 1k )
V
= A =0
2k
I SC = −
12V
= −18mA
1k || 2k
VOC
2
=
[ kΩ]
I SC 4 + (a / 1k )
RTH =
Solução do problema
RTH (a = 2 k )
Zerando as fontes para combinar as
resistências leva a um valor incorreto!!!!
V0 =
VOC
1k
VTH
1k + 1k + RTH
Tensão de circuito aberto
Obter Vo usando Thevenin
Super nó
V1
+
VTH
IX
IX
V1
V − (−3V )
− 1mA + 1
=0
2k
6k
Corrente de curto circuito
KVL
V11
V11 = 1000 I 1X I 1X =
− VTH − 1000 I X + V1 = 0
I SC
Variável controle
IX =
O circuito equivalente
RTH
1k
+
V11
2k
KCL
⇒ V11 = 0 ⇒ I 1X = 0
I SC = 1mA + ( −3V ) /(6k ) = 0.5mA
RTH =
V1 = (3 / 4)[V ]
VTH = (3 / 8)[V ]
I 1X
KVL
−
VOC
= (3 / 4 ) k
I SC
VTH
+
-
V0 =
2k
VO
_
2
(3 / 8)[V ]
2 + 1 + (3 / 4)
A resistência equivalente não pode ser obtida pela aproximação
“zerando” as fontes. Cuidado!!!
V1
2k
EXEMPLO: Usando Thevenin, obter Vo
Calcular Vo usando o equivalente de Thevenin
“Parte B”
V0 =
RTH
6k
11[V ]
6 k + 8k
VTH
Tensão circuito aberto
Equação de malha
I1 =
Variável de controle
V X1
; I 2 = 2mA
2000
VX1 = 4k ( I1 − I2 )
V X1 = 2kI1 ⇒ 2kI1 = 4k ( I1 − I 2 ) ⇒ I1 = 4mA
KVL para Voc
VOC = 2k * I1 + 3[V ]= 2k * 4mA + 3V = 11V
Equação de malha
Corrente de curto
I1
I1 =
I1 = 4mA
Vx"
; I 2 = 2mA
2000
− 3V + 2k ( I SC − I1 ) = 0
I sc
I SC =
Variável de controle
I2
Mesmo valor anterior
3V + 2k * I1 11
= mA
2k
2
Resistência de Thevenin
V X" = 4k * ( I1 − I 2 )
RTH =
VOC
11[V ]
=
= 2 kΩ
I SC (11 / 2) mA
EXEMPLO
Alternativa para troca de fontes
Linear Model for Transistor
R1
vS
Vx
a
+
R3 VTH
R2
+
-
g mVx
−
b
I SC
RTH
a
VTH =VOC, RTH =
VOC
ISC
Tensão de circuito aberto
VTH = − gm R3V x
Vx =
R2
RR
v S ⇒ VTH = − gm 3 2 v S
R1 + R2
R1 + R2
Corrente de curto circuito
VTH
+
-
I SC = − gmV x = − gm
b
R2
vS
R1 + R2
Resistência equivalente
RTH =
VOC
= R3
I SC
Teorema da Reciprocidade
45V
= 3A
15Ω
3A
= 1,5 A
I=
2
IS =
45V
= 4,5 A
10Ω
(6Ω).(4,5 A)
I=
= 1,5 A
12Ω + 6Ω
IS =
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
MÁXIMA TRANSFERÊNCIA DE POTÊNCIA
Courtesy of M.J. Renardson
http://angelfire.com/ab3/mjramp/index.html
PreAmp
(voltagem )
Para auto-falante
Modelo simplificado para
resistência do auto-falante...
RTH
RTH
VTH
VTH
+
-
SPEAKER
MODEL
+
-
MODELO BÁSICO PARA ANÁLISE
DE TRANSFERÊNCIA DE POTÊNCIA
MÁXIMA TRANSFERÊNCIA DE POTÊNCIA
Circuito de corrente contínua linear bilateral:
Potência transferida para carga máxima quando a
resistência da carga for exatamente igual à
resistência de Thévenin/Norton do circuito ligado a
esta carga : RL = RTh = RN
MÁXIMA TRANSFERÊNCIA DE POTÊNCIA
RTH
+
-
VTH
+
VL
−
SOURCE
PL =
RL
VL2
RL
V2
; VL =
VTH PL =
2 TH
( RTH + RL )
RL
RTH + RL
Para cada RL tem-se uma determinada potência.
Como obter o valor máximo?
RL
(LOAD)
Considerar PL em função de RL e encontrar o
valor máximo para cada função.
(R + RL )2 − 2 RL (RTH + RL )
dPL
= VTH2 TH
4 3
dRL
(
)
R
+
R
TH
L
Derivada igual a zero para obter o(s) ponto(s) extremos.
Para este caso o numerador deverá ser zero.
RTH + RL − 2 RL = 0 ⇒ RL* = RTH
Teorema da
Máxima Transferência
de Potência.
O valor da Potência
A carga que maximiza a transferência de potência para o circuito
máxima é:
é igual a resistência equivalente Thevenin do circuito.
PL (max) =
VTH2
4 RTH
SOMENTE NESTE CASO PRECISAMOS CALCULAR A
TENSÃO DE THEVENIN
Exemplo: máxima transferência potência
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Gráfico de PL x RL
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Gráfico de VL,IL x RL
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Eficiência com valor de RL
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
Exemplo de aplicação: alto-falante.
Robert L. Boylestad
Introductory Circuit Analysis, 10ed.
Conexão série e paralelo:
Copyright ©2003 by Pearson Education,
Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
DETERMINE RL FOR MAXIMUM POWER TRANSFER
EXEMPLO
a
Obter a resistência de Thevenin entre a – b.
b
O circuito contem somente fontes independentes ....
RTH = 4k + || 3k ,6k ||= 6k
Resistência para máxima
transferência de potência
Caso seja necessário obter o valor da
potência transferida, será necessário
determinar a tensão de Thevenin!!!
loop1 : I1 = 2mA
loop 2 : 3k * ( I 2 − I1 ) + 6k * I 2 + 3[V ] = 0
I2 = −
3[V ] 1
1
+ I1 = [ mA]
9k 3
3
KVL : VOC = 4k * I1 + 6k * I 2 = 10[V ]
PMX =
2
VTH
4 RTH
PMX =
100[V 2 ] 25
= [mW ]
4 * 6k
6
DETERMINE RL AND MAXIMUM POWER TRANSFERRE D
EXEMPLO
a
1. Obter o equivalente Thevenin em a - b
c
2. Para máxima transferência de potência
RL = RTH
d
Problema com fontes misturadas
PMX =
2
VTH
4 RTH
b
....É simplificado usando Thevenin
em c - d retirando 4 kΩ e RL.
loop1 : I1 = 4mA
loop 2 : − 2 kI X' + 2 kI 2 + 4 k ( I 2 − I1 ) = 0
1I
I2
I X' = I 2
Variável de controle:
I 2 = I1 = 4mA ⇒ VOC = 8[V ]
Corrente de curto circuito
I "X
=0
I SC = 4mA
RTH = 2k
RL = 6k
PMX =
8V
82
8
[mW ] = [ mW ]
4*6
3