Document

Capítulo 10 – Dinâmica do movimento
de rotação
10.1 – Torque
Força causa aceleração. O que causa aceleração angular?
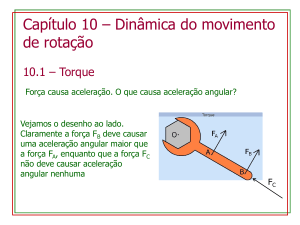
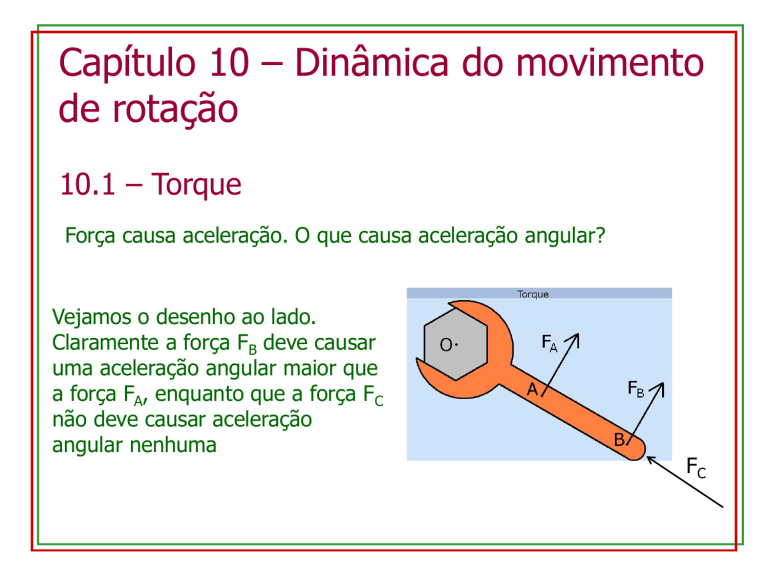
Vejamos o desenho ao lado.
Claramente a força FB deve causar
uma aceleração angular maior que
a força FA, enquanto que a força FC
não deve causar aceleração
angular nenhuma
FC
Torque:
Ftg = F senφ

F
φ

τ
O
 φ
r
l
 
τ = r × F (vetor torque)

Unidades S.I.: N.m
Direção e sentido: regra da mão direita
Módulo:

τ = τ = rF senφ = rFtg
Só há torque quando há componente tangencial da
força (força radial não produz torque)
Outra interpretação do torque:
l : Braço de alavanca
Exemplo: Y&F 10.1
τ = Fr senφ = Fl
10.2 – Torque e aceleração angular de um corpo
rígido Corpo rígido girando em torno de um eixo fixo: só a
componente tangencial da força produz aceleração angular
Componente
axial da força
Eixo de
rotação
Componente tangencial da força:
produz componente z do torque
Corpo
rígido
em
rotação
Trajetória
da
partícula
2ª Lei de Newton para a
componente tangencial:
Componente
radial da
força
F1,tg = m1a1,tg
F1,tg r1 = m1r1a1,tg = m1r12α z
Componente z
do torque
τ 1, z
F1,tg r1 = m1r12α z
I1
τ 1, z = I1α z
Momento de inércia
em relação ao eixo
Torque em relação a um ponto versus torque em relação a um eixo:

τ
β
τ = F1,tg r
τ z = τ senβ = F1,tg rsenβ = F1,tg r1
Somando por todas as partículas do CR:


2
=
τ
m
r

∑ i, z ∑ i i α z
i
∑τ

i
i,z
= Iα z

i
2ª Lei de Newton para rotação de um corpo rígido
Repare que a soma dos torques inclui apenas as forças externas
(os torques das forças internas se cancelam pela 3ª Lei de Newton)
Exemplos: Y&F 10.2 e 10.3
10.3 – Rotação de um corpo rígido em torno de
um eixo móvel
Movimento mais geral de um corpo rígido é a combinação da
translação do centro de massa com a rotação em torno de um eixo
que passa pelo centro de massa
Energia cinética de um corpo rígido (quadro-negro):
Energia cinética
de translação
1
1
2
K = MVcm + I cmω 2
2
2
Energia cinética
de rotação
Rolamento sem deslizamento:
Ponto de contato com a superfície deve permanecer instantaneamente
em repouso. Isto impõe a condição:
Vcm = Rω
Como já dissemos, o movimento pode ser visto como a combinação
da translação do centro de massa com a rotação em torno do eixo
que passa pelo centro de massa, de modo que a energia cinética
pode ser escrita como:
1
1
2
2
K=
2
MVcm +
2
I cmω
Alternativamente, o movimento pode ser visto, instantaneamente,
como uma rotação pura em torno do eixo que passa pelo ponto de
contato com a mesma velocidade angular ω:
Desta forma, a energia cinética é:
1
K = I1ω 2
2
Pelo Teorema dos Eixos Paralelos:
I1 = I cm + MR 2
v = ωR = Vcm
v = ω (2 R) = 2Vcm
Assim:
(
)
1
K = I cm + MR 2 ω 2
2
1
1
K = Mω 2 R 2 + I cmω 2
2
2
(de acordo com o
1
1
2
2
K = MVcm + I cmω resultado do slide
2
2
anterior)
Trajetória de um ponto qualquer de uma roda ou anel: ciclóide
http://www.youtube.com/watch?v=kr6-IZ925Cc&NR=1
Exemplos: Y&F 10.4 e 10.5 (kit LADIF)
Dinâmica do movimento combinado de translação e rotação:


∑ Fext = MAcm
Devemos usar as equações: 
∑τ z = I cmα z
Exemplos: Y&F 10.6 e 10.7
Demonstração LADIF: Carretel (fazer Problema Y&F 10.71)
10.4 – Trabalho e potência no movimento de
rotação
Criança aplicando força
tangencial em um carrosel

Ftg

Ftg
Trabalho infinitesimal: dW = Ftg ds = Ftg R dθ = τ z dθ
Trabalho total para deslocamento entre θ1 e θ2: W =
Se o torque for constante: W = τ z (θ 2 − θ1 ) = τ z ∆θ
θ2
∫θ τ
1
z
dθ
Teorema trabalho-energia cinética para o corpo rígido:
dω z
dθ
dW = τ z dθ = (Iα z )dθ = I
dω z = Iω z dω z
dθ = I
dt
dt
Integrando:
ω2
1 2 1 2
W = I ∫ ω z dω z = Iω2 − Iω1 = ∆K
2
2
ω1
Potência:
dW = τ z dθ
dW
dθ
=τz
dt
dt
P = τ z ω z (análogo a P = Fx v x )
Expandindo a analogia entre a cinemática linear de uma
partícula e a rotação de um corpo rígido em torno de um eixo
fixo:
Cinemática de uma partícula
Posição
Velocidade
Aceleração
Massa
Energia cinética
Força
Rotação de um CR em torno de
um eixo fixo
x
vx
Ângulo
ax
Aceleração angular
m
1 2
mv x
2
Fx
Velocidade angular
Momento de inércia
Energia cinética
Torque
θ
ωz
αz
I
1 2
Iω z
2
τz
∑ Fx,ext = max
2a. Lei
Trabalho
dW = Fx dx
Trabalho
Potência
P = Fx v x
dW = τ z dθ
Potência
P = τ zω z
2a. Lei
∑τ
z ,ext
= Iα z
Próximas aulas:
6a. Feira 11/11: Aula de Exercícios (sala A-327)
4a. Feira 16/11: Aula de Magna (sala A-343)