Exemplo - Google Groups

Condições de Equilíbrio
Uma vez que um corpo pode apresentar os
movimentos de translação e rotação, é
necessário
que
duas
condições
sejam
satisfeitas:
Para impedir a translação
Para impedir a rotação
 
FR  0


MR  0
Definição de um Sistema de Referência
 
FR  0


MR  0
F
F
F
x
0
y
0
z
0
M
M
M
x
0
y
0
z
0
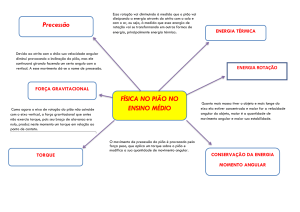
Momento (Torque) de uma Força
É uma grandeza física relacionada com a
tendência de giro de um corpo.
M  F.d.sena
Unidade no S.I.: N.m
F = força (N);
d = distância entre o ponto de aplicação da força
e o eixo de rotação (m);
a = ângulo formado entre os vetores F e d.
Momento (Torque) de uma Força
M  F .b
b  d . sen a
ou
M  Fy .d
Fy  F . sen a
M  F.d.sen a
O módulo do torque em
relação a um eixo é o
produto
força
do
módulo
da
pelo
braço
de
alavanca,
que
é
a
distância perpendicular
do eixo à linha de ação
da força.
Momento como Produto Vetorial
O momento exercido pela força F em
relação a um ponto de referência O se
define como o produto vetorial de d e F:
  
M  d F

i
  
M  d  F  dx
Fx

j
dy
Fy

k
dz
Fz
EXEMPLO
F = 100 N
M = F . d . sena
3m
a = 90 °
M = 100.3.sen90°
sen 90° = 1
M = 300 N.m
OBSERVAÇÃO:
Para que o MR seja nulo é
necessário
que
o
Momento
no
sentido horário seja igual ao
Momento no sentido anti-horário.
M
=M
F1 = 30kgf
A barra está em equilíbrio?
M
=M
120.20 = 30.80
2400 = 2400 OK!
EXERCÍCIO 1
Qual
situação
é
retirar o prego?
M = 7.30 = 210
mais
M = 10.25 = 250
favorável
para
M = 12.20 = 240
R.: Situação B, pois possui o maior momento.
EXERCÍCIO 2
Calcule o valor de x para que o homem consiga
equilibrar a barra com o urso do outro lado.
Despreze o peso da barra.
640 kg
80 kg
x
2m
640 kg
80 kg
x
M
2m
=M
PURSO . 2 = PHOMEM . x
640.10 . 2 = 80.10 . x
x = 16 m
EXERCÍCIO 3
Calcule a força exercida
segurar a bola de 5kgf.
M
=M
pelo
bíceps
5 . 32 = F1 . 4
F1 = 40 kgf
para
EXERCÍCIO 6
Uma escada uniforme está apoiada em uma
parede. Qual o valor mínimo do coeficiente de
atrito estático na interface escada-chão que
impedirá a escada de deslizar?
EXERCÍCIO 7
Em estudos sobre a fisiologia dos exercícios
é importante determinar o local do centro de
massa de uma pessoa, como mostrado na figura.
A que distância dos pés da mulher está
localizado o seu centro de massa?
1,80m
380N
320N
EXERCÍCIO 8
Uma tábua uniforme de 48N e 3,6m repousa
horizontalmente
sobre
dois
cavaletes,
conforme a figura. Quais as reações normais
exercidas pelos cavaletes sobre a tábua?
DESAFIO 1
Uma porteira de 480N está fixada em um mourão por
duas dobradiças, conforme a figura. O arame de
sustentação
está
colocado
de
modo
que
a
componente horizontal da força exercida pela
dobradiça
superior
seja
zero.
Calcule
a
componente horizontal da força exercida pela
dobradiça inferior e a tração no arame.
DESAFIO 2
Uma haste rígida está em equilíbrio estático
com uma força horizontal aplicada no seu
ponto médio. Despreze o peso da haste.
a) determine a tração no cabo, admitindo que
a haste não escorregue.
b) determine o mínimo e para que a haste não
escorregue.
Segunda lei de Newton para
Rotação
 Um torque pode causar uma rotação em um corpo rígido, por
exemplo quando abre ou fecha uma porta.
 Consideremos um corpo rígido de massa m na proximidade de
uma haste de massa desprezível e comprimento r. A haste se
move formando um círculo.
 Apenas a Ft pode acelerar a
partícula, assim usando a 2º
lei Newton
O torque que atua na partícula é
M  Ft  r  mat r
Segunda lei de Newton para
Rotação
como
teremos
M  mar r  mr a
2
A grandeza entre parênteses é o momento de inércia da partícula
em torno do eixo de rotação
M  Ia
Que é a equação de Newton para a rotação.
Momento Angular
 Consideremos uma partícula de massa m com momento linear
(p = mv) quando ela passa pelo ponto A em um plano xy. O
momento angular L desta partícula em relação à origem O é

  
 
L  r  p  mr  v 
→ S.I: kg m2/s. J.s
→ Sentido: regra da mão direita.
→ Módulo:
Momento angular 
Derivando o momento angular L em relação ao tempo:



dL d  
dr   dp
 (r  p) 
 p  r
dt dt
dt
dt
=0

como

 dp
f 
dt


dL  
 r f  M
dt
Conservação momento angular
Quando

 dL  

M
 r  f  0  L  constante
dt
se

M 0

i) f  0
ou


Li  L f
ou

ii) r  0

L  constante
 I ii  I f  f
Conservação momento angular
iii) quando a força é colinear com o vetor posição teremos também
Exemplo:

M 0
FORÇAS CENTRAIS, que são forças da forma
 

F (r )  f (r ) u
Neste caso:

 dL 

M
 r  f (r )u  0
dt

 L  constante
Conservação momento angular
Exemplo
I  mR
2


Li  L f
L  I
Quando a bailarina faz pirueta
 o momento de inércia I diminui
 a velocidade angular  aumenta
L  I  cte.
 I i i  I f  f
Conservação momento angular
No sistema homem - halteres só há forças internas e,
portanto o torque resultante externo é igual a zero
L  I  constante

f I f
i I i
Com a aproximação dos halteres (
I i i  I f  f
If
<
Ii
) a velocidade angular do sistema aumenta
Exemplo:
Exemplo:
Exemplo:
Exemplo: