Trabalho e Energia Cinética

Dinâmica de Rotação
Profª Jusciane da Costa e Silva
Rotação do Corpos
Introdução
O que ocorre com a força que
você realiza sobre a chave de
roda que ocasiona a rotação da
roda? De modo geral, o que
produz aceleração angular em
um corpo que gira?
 Definir o torque, que
descreve a ação giratória ou o
efeito de torção de uma força.
O torque efetivo que atua
sobre
um
corpo
rígido
determina
sua
aceleração
angular.
Introdução
 O que você pensa sobre o efeito
de uma força capaz de alterar o
movimento de rotação de um
corpo?
o módulo, a direção e o sentido da força
são importantes, mais o ponto de
aplicação da força também é relevante.
 Quanto mais distante do eixo de
rotação aplicar a força, mais fácil
será girar a porta.
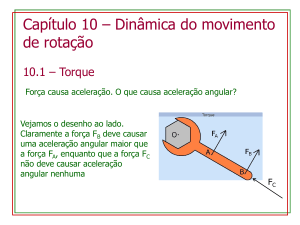
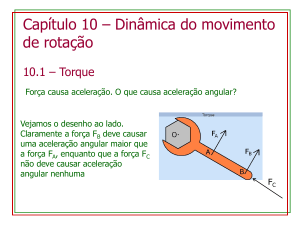
 Uma chave de boca é usada para
afrouxar uma porca presa firmemente.
TORQUE
 Consideremos uma força F aplicada num ponto P, cuja posição em
relação ao ponto O é definida pelo vetor posição r. Os vetores F e r
fazem um ângulo  um com o outro.
TORQUE
 Torque
Definimos o torque como sendo o produto dos dois fatores
Duas maneiras de calcular o torque
onde r é a distância perpendicular entre o eixo de rotação em O
e a linha de ação de F. Esta linha estendida é chamada de linha
de ação de F, e r é o braço da alavanca.
S.I: Newton.metro (N.m)
TORQUE
Torque é um vetor, portanto tem módulo,
direção e sentido.
Direção: quando r e F estão localizados
no plano perpendicular ao eixo de rotação, então o vetor torque tem o mesma
direção do eixo de rotação.
Sentido: dado pela regra da mão direita.
Segunda lei de Newton para Rotação
 Um torque pode causar uma rotação em um corpo rígido, por
exemplo quando abre ou fecha uma porta.
 Consideremos um corpo rígido de massa m na proximidade de
uma haste de massa desprezível e comprimento r. A haste se
move formando um círculo.
 Apenas a Ft pode acelerar a
partícula, assim usando a 2º
lei Newton
O torque que atua na partícula é
Segunda lei de Newton para Rotação
como
teremos
A grandeza entre parênteses é o momento de inércia da partícula
em torno do eixo de rotação
Que é a equação de Newton para a rotação.
Trabalho e energia Cinética de Rotação
 Translação: Vimos que quando uma força F acelera um corpo
rígido de massa m, ele realiza trabalho sobre o corpo. Assim K
pode mudar. (supondo que seja a única energia)
 Relacionando a variação K com W através do Teorema trabalhoenergia, temos
Para o movimento em um eixo.
Como a taxa do trabalho realizado por unidade de tempo é a
potência
Trabalho e energia Cinética de Rotação
 Para a Rotação: Um torque acelera um corpo rígido, ele realiza
trabalho. Portanto a energia cinética pode mudar também.
 Podemos calcular o trabalho, como
 Com o torque aplicado sendo constante
 Como o trabalho por unidade de tempo é a potencia, então
Que é a potência em torno
de um eixo fixo
Relações da Translação e Rotação
Rolamento
 Eixo móvel: que é combinação do movimento de translação e
rotação.
Com R sendo o raio da roda. A
velocidade linear do CM é ds/dt.
Portanto.
Energia Cinética de Rolamento
 Calcular a energia cinética de uma roda em rolamento,
descrevendo a rotação que passa por um eixo.
Com Ip sendo o momento de inércia no ponto P. Usando o teorema
dos eixos paralelos
Substituindo
Usando
, temos
Termo de rotação + termo de
translação.
Forças de Rolamento
 Se uma roda gira com v = constante ela não tem tendência a
deslizar no ponto P e portanto não existe F atrito.
 No entanto, se uma força age na roda causando uma aceleração
do CM faz com que a roda gire mais rápido ou não. Esta
aceleração tende a fazer com que a roda deslize
 Se a roda não desliza
A força é uma força de atrito estático e o rolamento é de
rolamento suave.
 quando a força de atrito atua sobre
o sistema fazendo com que seu movi mento não seja suave, dizemos que a
força que existe é uma força de atrito
cinético.
Forças de Rolamento
 Consideremos um corpo redondo de massa M e raio R rolando
suavemente para baixo ao logo do eixo x em uma rampa
inclinada de ângulo .
 Queremos
encontrar
uma
expressão para a aceleração acm
descendo a rampa.
 Após algumas manipulações
Momento Angular
 Consideremos uma partícula de massa m com momento linear (p
= mv) quando ela passa pelo ponto A em um plano xy. O
momento angular L desta partícula em relação à origem O é
 S.I: kg m2/s. J.s
 Sentido: regra da mão direita.
 Módulo:
Momento Angular
Vimos que
De forma análoga
O momento angular de um sistema de partícula é o somatório de
cada momento angular das partículas individuais.
Momento Angular
Os momentos angulares das partículas individuais podem variar
com o tempo, quer devido a influência externas que podem atuar
sobre o sistema.
Portanto
“ o torque externo resultante atuando sobre um sistema de
partículas é igual à taxa de variação temporal do momento
angular total L do sistema.”
Momento Angular
Vamos calcular o momento a angular de
um sistema de partículas que formam
um corpo rígido que gira em torno de
um eixo
Estamos interessados na componente
paralela ao eixo de rotação
Somando todas as contribuições
Conservação do Momento Angular
Quando o torque resultante externo é igual a zero
Exemplos:
O voluntário que gira:
Conservação do Momento Angular
Quando o homem recolhe o braço diminui o momento de inércia e
como o momento é constante, a velocidade angular aumenta.
A praticamente de saltos ornamentais:
Uma nadadora executa um salto mortal
frontal de uma volta e meia. Seu CM segue uma trajetória parabólica.
Ela deixa o trampolim com L, em torno
do eixo que passa pelo CM.
Nenhum torque externo age, portanto
L se conserva.