EXERCÍCIOS DO PRP03_V2

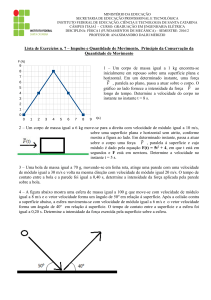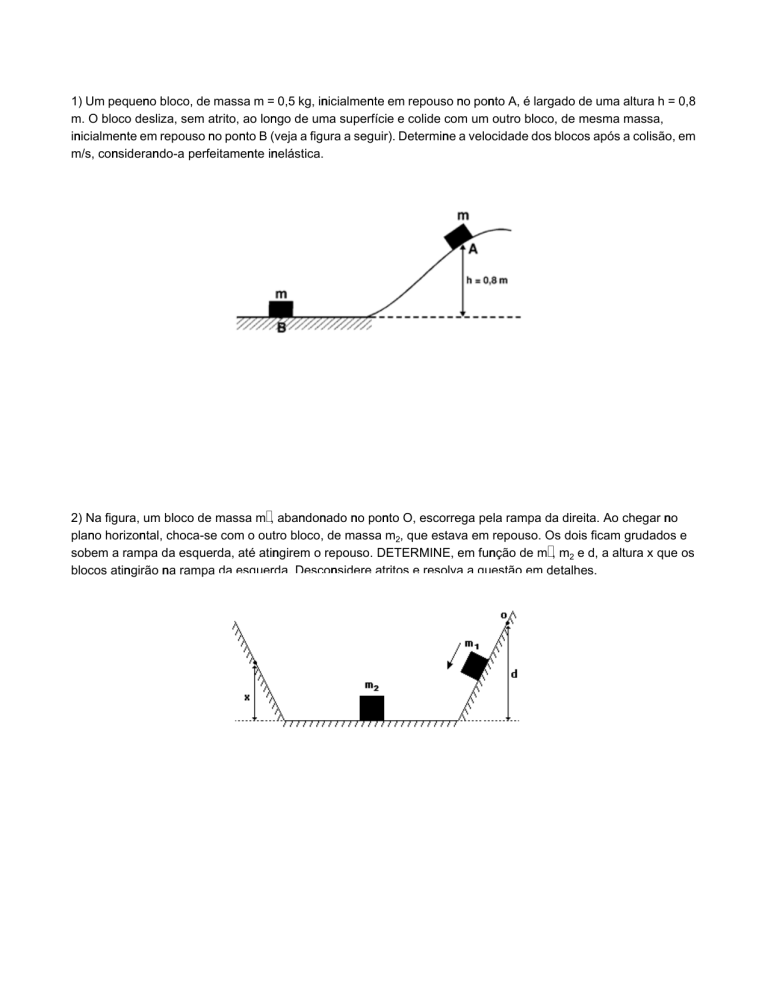
1) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma altura h = 0,8
m. O bloco desliza, sem atrito, ao longo de uma superfície e colide com um outro bloco, de mesma massa,
inicialmente em repouso no ponto B (veja a figura a seguir). Determine a velocidade dos blocos após a colisão, em
m/s, considerando-a perfeitamente inelástica.
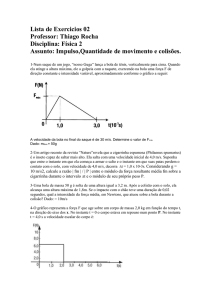
2) Na figura, um bloco de massa m•, abandonado no ponto O, escorrega pela rampa da direita. Ao chegar no
plano horizontal, choca-se com o outro bloco, de massa m‚, que estava em repouso. Os dois ficam grudados e
sobem a rampa da esquerda, até atingirem o repouso. DETERMINE, em função de m•, m‚ e d, a altura x que os
blocos atingirão na rampa da esquerda. Desconsidere atritos e resolva a questão em detalhes.
3) A figura mostra uma mesa de bilhar sobre a qual encontram-se duas bolas de mesma massa. A bola (1) é
lançada em linha reta com uma velocidade v³ e vai se chocar frontalmente com a bola (2), que se encontra em
repouso.
Considere o choque perfeitamente elástico e despreze os atritos.
Calcule, em função de v³, as velocidades que as bolas (1) e (2) adquirem após o choque.
4) Um carro A, de massa m, colide com um carro B, de mesma massa m que estava parado em um cruzamento.
Na colisão os carros se engastam, saem juntos, arrastando os pneus no solo, e percorrem uma distância d até
atingirem o repouso, como ilustram as figuras a seguir.
a) Calcule a razão EÝ'/EÝ entre a energia cinética do sistema constituído pelos dois carros após o choque (EÝ') e a
energia cinética do carro A antes do choque (EÝ).
b) Medindo a distância d e o coeficiente de atrito de deslizamento ˜ entre os pneus e o solo, conhecendo o valor
da aceleração da gravidade g e levando em consideração que os carros tinham a mesma massa m, a perícia
técnica calculou o módulo vÛ da velocidade do carro A antes da colisão.
Calcule vÛ em função de ˜, d e g.
5) Uma esfera de massa igual a 100g está sobre uma superfície horizontal sem atrito, e prende-se à extremidade
de uma mola de massa desprezível e constante elástica igual a 9N/m. A outra extremidade da mola está presa a
um suporte fixo, conforme mostra a figura (no alto, à direita). Inicialmente a esfera encontra-se em repouso e a
mola no seu comprimento natural. A esfera é então atingida por um pêndulo de mesma massa que cai de uma
altura igual a 0,5m. Suponha a colisão elástica e g=10m/s£.
Calcule:
a) as velocidades da esfera e do pêndulo imediatamente após a colisão;
b) a compressão máxima da mola.
6) No esquema a seguir estão representadas as situações imediatamente anterior e posterior à colisão
unidimensional ocorrida entre duas partículas A e B.
Sendo conhecidos os módulos das velocidades escalares das partículas, calcule a relação mÛ/m½ entre as
massas.
7) O pêndulo balístico é um sistema utilizado para medir a velocidade de um projétil que se move rapidamente. O
projétil de massa m• é disparado em direção a um bloco de madeira de massa m‚, inicialmente em repouso,
suspenso por dois fios, como ilustrado na figura. Após o impacto, o projétil se acopla ao bloco e ambos sobem a
uma altura h.
a) Considerando que haja conservação da energia mecânica, determine o módulo da velocidade do conjunto
bloco-projétil após o impacto.
b) A partir do princípio da conservação da quantidade de movimento, determine a velocidade inicial do projétil.
8) Uma pequena esfera rola sobre a superfície plana e horizontal de uma mesa, como mostra a figura adiante.
Desprezando a resistência oferecida pelo ar, pode-se afirmar que, durante o movimento de queda da esfera, após
abandonar a superfície da mesa, permanecem constantes:
a) a aceleração e a força que age na esfera.
b) a aceleração e a quantidade de movimento da esfera.
c) a velocidade e a força que age na esfera.
d) a velocidade e a quantidade de movimento da esfera.
e) a velocidade e a aceleração de esfera.
9) Um bloco de massa 0,10kg desce ao longo da superfície curva mostrada na figura adiante, e cai num ponto
situado a 0,60m da borda da superfície, 0,40s depois de abandoná-la.
Desprezando-se a resistência oferecida pelo ar, pode-se afirmar que o módulo (intensidade) da quantidade de
movimento do bloco, no instante em que abandona a superfície curva é, em kg.m/s,
a) 0,10.
b) 0,15.
c) 0,20.
d) 0,25.
e) 0,30.
10) Um atirador, com uma metralhadora, pode resistir a uma força média de recuo de, no máximo, 160N. As balas
têm massa 40 g cada uma e saem da metralhadora com velocidade de 800m/s. O número máximo de projéteis
que podem ser atirados por segundo é:
a) 16.
b) 10.
c) 8.
d) 5.
e) 4.
11) Um móvel, de massa 5,0kg, tem movimento retilíneo uniforme quando recebe a ação de uma força, na mesma
direção e sentido da velocidade, que varia com o tempo conforme o gráfico a seguir. A aceleração média
produzida pela força, no tempo considerado, em m/s£, é igual a :
a) 2
b) 3
c) 4
d) 5
e) 6
12) O gráfico representa a força resultante sobre um carrinho de supermercado de massa total 40 kg, inicialmente
em repouso.
A intensidade da força constante que produz o mesmo impulso que a força representada no gráfico durante o
intervalo de tempo de 0 a 25 s é, em newtons, igual a
a) 1,2
b) 12
c) 15
d) 20
e) 21
13) Uma nave espacial de 10¤kg se movimenta, livre de quaisquer forças, com velocidade constante de 1m/s, em
relação a um referencial inercial. Necessitando pará-la, o centro de controle decidiu acionar um dos motores
auxiliares, que fornecerá uma força constante de 200N, na mesma direção, mas em sentido contrário ao do
movimento. Esse motor deverá ser programado para funcionar durante:
a) 1s.
b) 2s.
c) 4s.
d) 5s.
e) 10s.
14) Uma esfera de massa 20g atinge uma parede rígida com velocidade de 4,0m/s e volta na mesma direção com
velocidade de 3,0m/s. O impulso da força exercida pela parede sobre a esfera, em N.s, é, em módulo, de
a) 0,020
b) 0,040
c) 0,10
d) 0,14
e) 0,70
15) Duas partículas, de massas m• e m‚, colidem frontalmente. A velocidade de cada uma delas, em função do
tempo, está representada no gráfico:
A relação entre m• e m‚ é:
a) m‚ = 5m•
b) m‚ = 7m•
c) m‚ = 3m•/7
d) m‚ = 7m•/3
e) m‚ = m•
16) Cada esquema, a seguir, revela as situações observadas imediatamente antes e depois da colisão entre dois
objetos. Nestes esquemas, a massa de cada objeto é dada em quilograma e a velocidade em metro por segundo.
O esquema que corresponde à colisão perfeitamente elástica é o indicado na opção:
17) A figura mostra o gráfico das velocidades de dois carrinhos que se movem sem atrito sobre um mesmo par de
trilhos horizontais e retilíneos. Em torno do instante 3 segundos, os carrinhos colidem.
Se as massas dos carrinhos 1 e 2 são, respectivamente, m• e m‚, então
a) m• = 3m‚.
b) 3m• = m‚.
c) 3m• = 5m‚.
d) 3m• = 7m‚.
e) 5m• = 3m‚.
GABARITO
1. V(depois da colisão) = 2,0 m/s
2. x = d.[m•/(m•+m‚)]£
3. v• = 0
v‚ = v³
4. a) EÝ'/EÝ = 1/2
b) vÛ½ = 2 Ë(2˜ g d)
5. Na colisão elástica o momento é conservado e a velocidade relativa troca de sinal. Então:
Mv• = Mu• + Mu‚
v• = u‚ + u•
v• = u• + u‚
v• = u‚ - u•
A solução é u•=0 e u‚=v•.
a) Usando a lei de conservação da energia calculamos a velocidade após a colisão: (MV£)/2=Mgh ou u‚=Ë10m/s.
b) x = 1/3 m
6. mÛ/m½ = 5/4
7. a) v• = Ë2 g h
b) v³ = [(m•+m‚)/m•] Ë2 g h
8. [A]
9. [B]
10. [D]
11. [A]
12. [E]
13. [D]
14. [D]
15. [A]
16. [A]
17. [E]