Fração (FT n.º 8) - Agrupamento Escolas João da Silva Correia

Agrupamento de Escolas João da Silva Correia
Escola EB 2,3
Matemática – 5º Ano – Ficha de Trabalho n.º _____
FTM5010a
Aluno: __________________________________________________________ Turma: ______ Nº: ______
Assunto: A fração como representação de medida de comprimento e de outras grandezas.
Na semirreta numérica abaixo representada verificamos que o segmento de reta correspondente à unidade
está dividido em 10 segmentos iguais.
0
A
B
C
D
1
O ponto A corresponde ao comprimento do primeiro segmento; então corresponde à fração
1
.
10
O ponto B corresponde ao comprimento de 4 desses segmentos alinhados, a partir do zero; então
corresponde à fração
4
.
10
Indica as frações correspondentes a:
C  ____
D ____
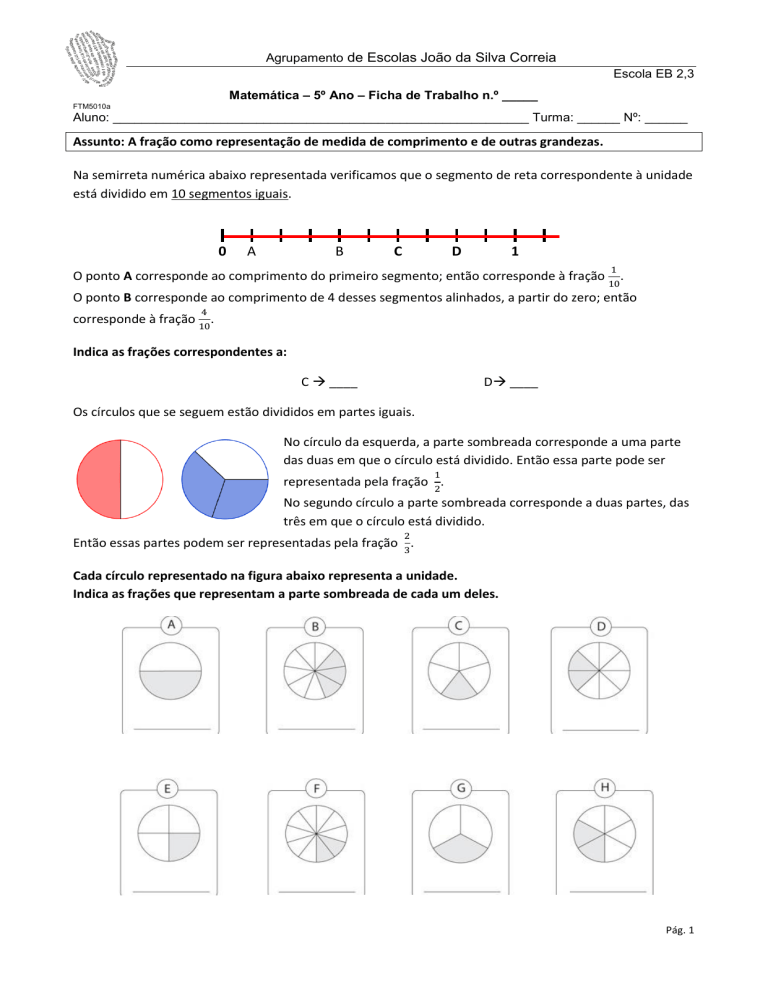
Os círculos que se seguem estão divididos em partes iguais.
No círculo da esquerda, a parte sombreada corresponde a uma parte
das duas em que o círculo está dividido. Então essa parte pode ser
1
representada pela fração 2.
No segundo círculo a parte sombreada corresponde a duas partes, das
três em que o círculo está dividido.
2
3
Então essas partes podem ser representadas pela fração .
Cada círculo representado na figura abaixo representa a unidade.
Indica as frações que representam a parte sombreada de cada um deles.
Pág. 1
Identificação dos termos da fração:
2
3
Vamos considerar, por exemplo, a fração .
2
3
NUMERADOR - Número das partes iguais que considero.
 Traço de fração
DENOMINADOR - Número de partes iguais em que está dividida a unidade.
A fração como quociente
O José comprou uma piza que estava dividida em 3 partes iguais. Que parte da piza comeu o José?
Repara que 1 ÷ 3 = 0,333 … O quociente não é exato.
Então, podemos escrever: 1 ÷ 3 =
1
3
Deste modo podemos escrever qualquer quociente.
Qualquer fração representa o quociente do numerador pelo denominador.
10
2
= 10 ÷ 2 = 5
7
4
1
6
= 7 ÷ 4 = 1,75
Repara que agora posso escrever o quociente exato de 1 por 6.
= 1 ÷ 6 = 0, 1666 …
1÷6 =
1
6
Números racionais não negativos
Já deves ter reparado que o tema que estamos a estudar se designa “Números racionais não negativos”.
Mas o que são números racionais?
Números racionais são todos aqueles que se podem representar através de uma fração.
Tem em atenção que agora só vamos falar dos números racionais não negativos (inclui-se o zero).
Assim, uma fração pode representar:

Um número natural, quando o quociente do numerador pelo denominador é qualquer número
natural ou zero.
Isto acontece quando o numerador é divisível (ou múltiplo) do denominador. Como por exemplo:
15
3

8
2
= 15 ÷ 3 = 5
0
7
=8 ÷2 =4
=0 ÷7 =0
Um número fracionário quando o quociente do numerador pelo denominador não é exato (quando
o numerador não é divisível, ou não é múltiplo, do denominador). Como por exemplo:
7
4
1
3
= 7 ÷ 4 = 1,75
= 1 ÷ 3 = 0,333 …
Quais das seguintes frações representam números naturais
75
13
27
30
17
24
24
5
3
9
10
7
3
2
Pág. 2
Fração
Leitura
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
1
10
1
11
1
20
1
100
1
1000
2
3
5
2
3
4
9
5
7
8
Completa:
Numerador Denominador
Fração
Leitura da fração
7
8
8
9
Cinco sétimos
1
2
1
3
Pág. 3
Medir com frações
1. O segmento de reta [AB] representa a unidade.
Indica a fração que corresponde aos segmentos de reta:
a)
b)
c)
2. O segmento de reta [AB] representa a unidade.
Indica a fração que corresponde aos segmentos de reta:
a)
b)
c)
d)
e)
f)
Pág. 4
3. Representa a unidade sabendo que:
a) O segmento [AB] corresponde a um terço da unidade.
b) O segmento [CD] corresponde a um quarto da unidade.
c) O segmento [EF] corresponde a um meio da unidade.
4. Localiza na semirreta seguinte as seguintes frações:
1
10
1
;
2
1
;
5
5. Localiza na semirreta seguinte as seguintes frações:
1
8
;
1
2
;
1
4
6. Identifica as frações representadas pelos pontos A, B, C e D.
A=
B=
C=
D=
7. Representa a unidade sabendo que:
a) A figura
b) A figura
c) A figura
corresponde a um meio da unidade.
corresponde a dois terços da unidade.
corresponde a três quartos da unidade.
Pág. 5
8. Observa a semirreta que segue.
a) Localiza na semirreta acima os seguintes números:
b) Identifica as frações representadas pelos pontos A, B e C.
A=
B=
C=
9. Para cada uma das figuras, indica a fração correspondente à parte pintada.
10. Pinta, em cada caso, a fração indicada.
Pág. 6