Document

Cinemática vetorial
Cinemática vetorial
Deslocamento, velocidade e aceleração
Grandezas físicas vetoriais
Módulo (intensidade), direção e sentido
Deslocamento vetorial: d
B
d
A
Velocidade vetorial média: vm
d
vm =
Dt
O vetor velocidade média
𝑣𝑚 tem a mesma direção e o
mesmo sentido do vetor deslocamento 𝑑 .
Módulo da velocidade vetorial média
e valor absoluto da velocidade
escalar média: v  Ds 
 m

Dt 

d  Ds  v m  v m
d  Ds  v m  v m
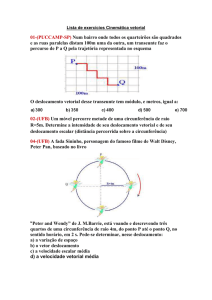
Exemplo 1
Um escoteiro, ao fazer um exercício de marcha com seu pelotão,
parte de um ponto P e sofre a seguinte sequência de
deslocamentos:
I. 800 m para o Norte;
II. 300 m para o Oeste;
III. 400 m para o Sul.
Sabendo que a duração da marcha é de 8 min 20 s e que o
escoteiro atinge um ponto Q, determine:
a) O módulo do seu deslocamento vetorial de P a Q;
b) O módulo da velocidade vetorial média e da velocidade escalar
média de P a Q.
Exemplo 2
Um ônibus percorre em 30 minutos as ruas de um bairro, de A até
B, como mostra a figura:
Determine o módulo da velocidade vetorial média e da velocidade
escalar média em km/h.
Velocidade vetorial instantânea: 𝒗
A velocidade vetorial instantânea (vetor velocidade) é igual a
velocidade vetorial média para o instante t2 muito próximo de t1.
.
B’ t2
t2
.
Sentido do
movimento
B’’
A
t1
.
B t2
𝒗m
Trajetória
Sentido do
movimento
𝒗
A
t1
Trajetória
Reta tangente ao ponto A
Direção: a mesma da reta tangente à trajetória, passando
pelo ponto A;
Sentido: o mesmo do movimento;
Módulo: igual ao valor absoluto da velocidade escalar v no
instante t.
Aceleração vetorial: 𝒂
𝒗𝟐
B
t2
Sentido do
movimento
𝒗𝟏
A
t1
Trajetória
𝒗𝟐
∆𝒗 𝒗𝟐 − 𝒗𝟏
𝒂=
=
∆𝒕
𝒕𝟐 − 𝒕𝟏
∆𝒗
𝒂
−𝒗𝟏
𝒗
Sentido do
movimento
𝒂𝒕
𝒂
𝒂𝒄𝒑
.C
Trajetória
𝒂𝒕 → é denominada aceleração tangencial. Possui como
papel modificar o módulo do vetor velocidade.
𝒂𝒄𝒑 → é denominada aceleração centrípeta. Possui como
papel modificar a direção do vetor velocidade. Aponta para o
centro da curva.
Aceleração vetorial: 𝒂
a  a t  a cp
at: Aceleração tangencial
acp: Aceleração centrípeta
 at  
 a cp
v2

R
2
a 2  a 2t  a cp
Movimento acelerado
Movimento retardado
Casos Particulares
MRU – Movimento Retilíneo Uniforme
MCU – Movimento circular Uniforme
MRUV – Movimento retilíneo
uniformemente variado
MCUV – Movimento circular
uniformemente variado
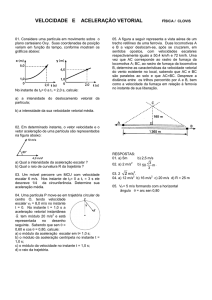
Exemplo 3
Uma partícula descreve um movimento uniformemente variado e
acelerado no sentido horário. Represente a velocidade vetorial 𝑣 ,
a aceleração centrípeta 𝑎 𝑐𝑝, a aceleração tangencial 𝑎 𝑡 e a
aceleração resultante 𝑎, no instante em que a partícula passa pelo
ponto P indicado.
Exemplo 4
Um ponto material percorre uma trajetória circular de raio R = 20
m com movimento uniformemente variado e aceleração escalar α
= 5 m/s². Sabendo-se que no instante t = 0 sua velocidade
escalar é nula, determine no instante t = 2 s os módulos da:
a)
b)
c)
d)
Velocidade vetorial;
Aceleração tangencial;
Aceleração centrípeta;
Aceleração vetorial.