Segunda lista de exercícios de Resistência dos Materiais e

Segunda lista de exercícios de Resistência dos Materiais e Estruturas − CIV 107
5.2.1 – Calcule o momento de inércia à torção ( J ) de um eixo maciço com seção transversal circular e
que tem diâmetro D = 50 mm. Resposta: J = 613.592,32 mm4
5.2.2 – Calcule o momento de inércia à torção ( J ) de um eixo com seção transversal circular vazada.
Dados: De = 12,0 cm e Di = 8,0 cm. Resposta: J = 1.633,63 cm4
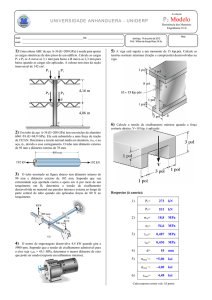
5.4.1 – Um eixo de seção transversal circular vazada fica solicitado pelos momentos de torção indicados
na figura abaixo. Calcule a tensão de cisalhamento máxima. Resposta: τmáx = 0,42 MPa
5.4.2 – Para o eixo do exercício 5.4.1 calcule o giro relativo da seção transversal B em relação ao engaste
indeformável A. Dado: G = 40 GPa. Resposta: θB = 9,55 x10 − 4 rad.
5.4.3 – Calcule as reações TA e TB nos engastes indeformáveis A e B e a tensão de cisalhamento máxima
que ocorre no eixo. Dado: T = 50 kN.mm.
Resposta: TA = 18.750 N.mm; TB = 31.250 N.mm; τmáx = 7,35 MPa
6.1.1 – Construa os diagramas de esforços internos (momento fletor e força cortante) da viga abaixo.
6.1.2 – Construa os diagramas de esforços internos da viga abaixo.
Resposta: Mmáx positivo = 9.333,3 N.m; Mmáx negativo = – 12.000 N.m; Vmáx = 7.266,67 N
6.1.3 – Calcule o maior momento fletor e a maior força cortante que solicitam a viga abaixo.
Resposta: Mmáx = 56.250 N.m; Vmáx = 45.000 N
Anexo Ι – Calcule o momento de inércia em relação ao eixo horizontal do centróide (Ιz) das duas áreas
abaixo. Resposta: a) Ιz = 31.906,8 mm4; b) Ιz = 4.920.000 mm4
6.3.1 – Calcule a tensão normal nos pontos a, b, c e d devidas ao momento fletor M = 2,0 x 105 N.mm.
Resposta: σa= − 94,02 MPa; σb= − 62,68 MPa; σc = 62,68 MPa; σd = 94,02 MPa
6.4.1 – Calcule as tensões máximas de tração e de compressão e a maior tensão cisalhante.
Resposta: σmax t = 11,25 MPa; σmax c = − 11,25 MPa; τmáx = 1,12 MPa
6.4.2 – Calcule as tensões normais extremas e a maior tensão cisalhante.
Resposta: σmax t = 16,20 MPa; σmax c = − 16,20 MPa; τmáx = 1,35 MPa
6.4.3 – Calcule a maior tensão normal de tração, a maior tensão normal de compressão e a tensão de
cisalhamento máxima. Resposta: σmáx t = 4,0 MPa; σmáx c = − 4,0 MPa; τmáx = 0,182 MPa
6.4.4 – Calcule as tensões normais extremas e a maior tensão cisalhante.
Resposta: σmax t = 20,5 MPa; σmax c = − 20,5 MPa; τmáx = 0,406 MPa
6.7.1 – Em um ensaio em laboratório mediu-se a deflexão máxima da viga abaixo: v máx = 5 mm. Sendo
E I = constante calcule o valor do módulo de elasticidade da viga. Resposta: E = 14,34 x 109 N/m2
6.7.2 – Calcule a deflexão (flecha) máxima da viga abaixo. E I = constante. Dado: E = 205 GPa.
Resposta: v máx = 3,81 x 10 − 4 m
7.1.1 – Calcule no engaste as tensões normais extremas e τmáx.
Resposta: σmáx t = 0,944 MPa; σmáx c = − 1,72 MPa; τmáx = 0,033 MPa