recuperação semestral

GOIÂNIA, ____ / ____ / 2015
PROFESSOR: Vinícius Camargo
DISCIPLINA: Matemática
SÉRIE: 8º ano
ALUNO(a):_______________________________
No Anhanguera você é
RECUPERAÇÃO SEMESTRAL
+ Enem
1. Numa partida de Futebol, 1/4 torciam pelo time A, 1/6 para o time B e 2000 pessoas não torciam por
nenhum dos dois times. Quantas pessoas assistiram ao jogo?
2. Douglas tem uma caixa de tomates. No domingo, 1/8 dos tomates da caixa estragaram; na segundafeira estragou 1/3 do que sobrou de domingo. Sobraram 70 tomates em boas condições. Calcule o
total de tomates na caixa?
3. Junior ganhou um pacote de bolinhas. No primeiro dia perdeu 1/4 das bolinhas, no 2º dia perdeu a
terça parte do que restou e sobraram ainda 50 bolinhas. Qual o número total de bolinhas?
4. Durante uma festa, as crianças tomaram metade dos refrigerantes, os adultos tomaram a terça parte
do que havia restado e ainda sobraram 120 garrafas cheias. Qual era o total de refrigerantes?
5. A soma de dois números é 20. Calcule-os, sabendo que o número maior é 3/2 do número menor.
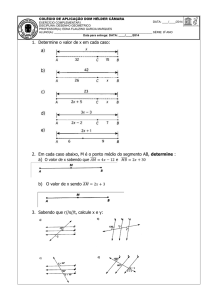
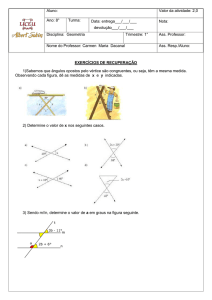
6. Calcule os ângulos indicados pelas letras nas figuras abaixo:
a)
b)
108º
x
x
y
17º
y
w
z
z
95º
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
c)
d)
120º
y
y
2x – 30º
45º
x
z
3x + 20º
7. Calcule o valor de x e y observando as figuras abaixo:
a)
b)
3x – 15º
y
60º
y
5x – 15º
4x + 5º
8. Duas retas paralelas cortadas por uma transversal determinam dois ângulos colaterais internos, em
que a medida de um deles é o triplo da medida do outro. A diferença entre as medidas dos ângulos
obtuso e agudo é igual a:
9. Uma reta transversal corta duas paralelas formando ângulos correspondentes cujas medidas são
expressas por (5x – 48º) e
(3x + 12º). A medida de cada ângulo agudo formado é igual a:
10. Usando as propriedades com potências de mesma base, transformem em uma só potência as
expressões:
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
2
 1   1
−  − 
a)  3  .  3 
 3  4 
 +  
 7  
b) 
3
3
7
11
6
c) (+ 1,9 ) : (+ 1,9 )
 1  1 
+  + 
d)  2  :  2 
3
11. Calcule as potências:
 − 3


a)  2 
2
 5
+ 
b)  4 
2
 1
− 
c)  2 
5
a −m =
12. Calcule as seguintes potências com expoente negativo: Não esqueça:
a) 10
−2
 5
− 
b)  8 
−2
 3
− 
c)  2 
1
am
−3
−3
d) (− 3)
e
13. Classifique cada sentença seguinte em verdadeira (V) ou Falsa (F). Justifique sua resposta:
a) (8 )
3 2
= 85
()
 10 4 
 5  = 10 −1
10 
b) 
()
2
2
c) (5 + 3) = 5 + 3
()
3
2
6
d) 4 .4. 4 = 4
14. Determine o valor desta expressão:
(− 1)3 − (− 1)4 + (− 2 )2 − 2 3 + (− 1 − 1)2
15. Com uma lata de tinta, pinto um quadrado de 676 metros quadrados.
Qual é a medida, em metros, do lado desse quadrado?
16. Determine a soma do quadrado de 310 com cubo de 220.
17. Um número natural é expresso por 11³ - 3³. 3. Qual é esse numero natural?
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
()
18. Encontre a soma dos quadrados dos números 10 e 5. O valor obtido é o cubo de qual numero?
19. Determine a raiz quadrada do valor de 2³ + 2 X 2².
20. Escreva o nome de 10 polígonos diferentes e determine quantos lados ele possui.
21. Quais os principais elementos de um polígono?
22. Considerando que F = {x | x é estado do sudeste brasileiro} e G = {x | x é capital de um país
sulamericano}, quais das sentenças seguintes são verdadeiras?
a) Rio de Janeiro
b) México
c) Lima
F
G
G
d) Montevidéu
G
e) Espírito Santo
f) São Paulo
F
F
23. Represente, na forma de diagrama, os seguintes conjuntos:
a) A = {x
N | 2 < x ≤ 12}
b) B = {x
N | 4 < x < 8}
24. Considere que:
•
•
•
A é o conjunto dos números naturais ímpares menores do que 10;
B é o conjunto dos dez primeiros números naturais;
C é o conjunto dos números primos menores do que 9.
Use os símbolos ⊂ ou ⊄ e relacione esses conjuntos na ordem dada:
a) A e B
b) C e A
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
c) C e B
d) A e C
25. Dados os conjuntos A = {p, q, r}, B = {r, s} e C = {p, s, t}, determine os conjuntos:
a) A ∪ B
b) A ∪ C
c) B ∪ C
d) A ∩ B
26. Represente os conjuntos A = {1, 2, 3, 5, 12}, B = {1, 2, 7, 8, 11} e C = {2, 4, 5, 8, 9} por meio
de um diagrama. A seguir, hachure a região que representa (A ∪ C) ∩ B.
27. A soma das medidas dos ângulos internos de um polígono regular é 2160º. Determine o
número de lados desse polígono.
28. Qual é o polígono convexo em que a soma dos ângulos internos é 1080°?
29. CALCULE o valor numérico das seguintes expressões algébricas:
a) 3a – 2b – 10 para a = 6 e b = -3
b) m² + 6 mn + n² para m =2 e n = -3
30. Dados os seguintes monômios, complete o que se pede:
a) 25 a²
b) – 3x²z³
c)
Coeficiente numérico
Coeficiente numérico
Parte literal
Parte literal
a³
d) - 4 ³ Coeficiente numérico
Coeficiente numérico
Parte literal
Parte literal
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
31. CALCULE:
a) 6a – 3a + 2a =
b) -2y² - 7y² + 5y²=
32. CALCULE:
7y – ( -2y + y) + ( - 3y + 5y)
33. CALCULE o perímetro e a área da seguinte figura:
5,6a
3,8a
34. Qual é o polígono convexo em que a soma dos ângulos internos é 1080°?
35. A soma dos ângulos internos de um polígono regular é 2880°. Determine:
a) O número de lados do polígono.
b) A medida do ângulo interno do polígono.
c) A medida do ângulo externo do polígono.
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.