Física I A e D 2006/2007 - 1.o Teste

dfg213ba
Física I A e D 2006/2007 - 1.o Teste - 2.a parte
Responda aos seguintes três problemas. Apresente todas as etapas utilizadas para resolver cada problema, justificando-as cuidadosamente, e apresente um resultado numérico,
sempre que tal seja pedido.
Em todas os problemas, utilize para a aceleração resultante da gravidade o valor
g = 10 m/ s2 .
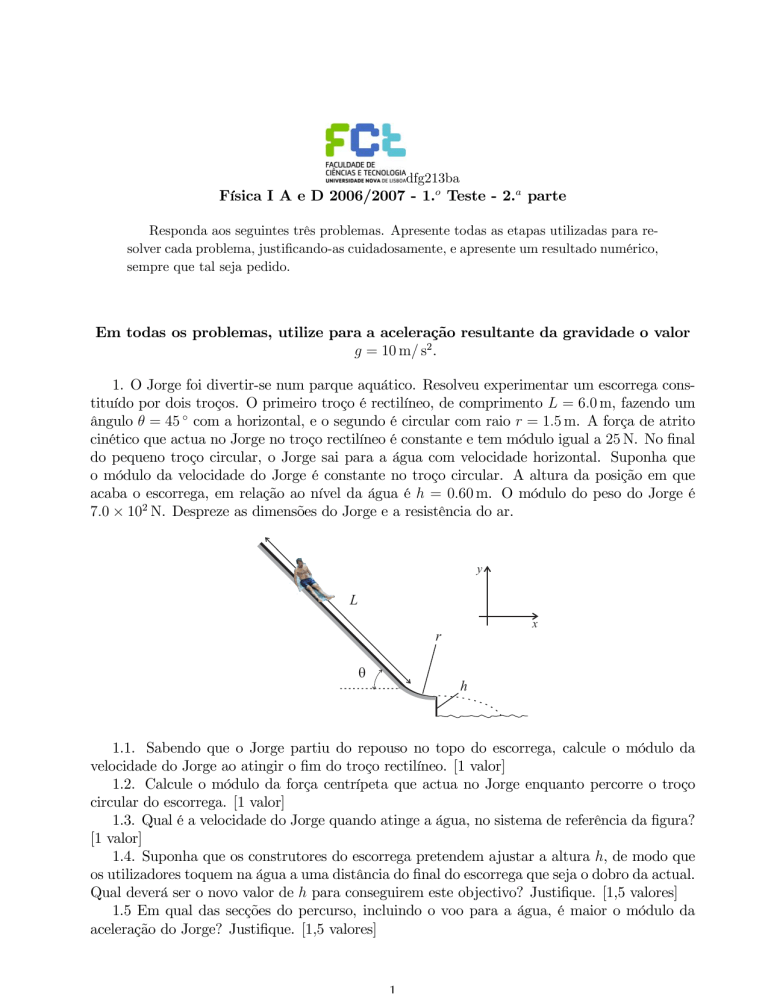
1. O Jorge foi divertir-se num parque aquático. Resolveu experimentar um escorrega constituído por dois troços. O primeiro troço é rectilíneo, de comprimento L = 6.0 m, fazendo um
ângulo θ = 45 ◦ com a horizontal, e o segundo é circular com raio r = 1.5 m. A força de atrito
cinético que actua no Jorge no troço rectilíneo é constante e tem módulo igual a 25 N. No final
do pequeno troço circular, o Jorge sai para a água com velocidade horizontal. Suponha que
o módulo da velocidade do Jorge é constante no troço circular. A altura da posição em que
acaba o escorrega, em relação ao nível da água é h = 0.60 m. O módulo do peso do Jorge é
7.0 × 102 N. Despreze as dimensões do Jorge e a resistência do ar.
y
L
x
r
q
h
1.1. Sabendo que o Jorge partiu do repouso no topo do escorrega, calcule o módulo da
velocidade do Jorge ao atingir o fim do troço rectilíneo. [1 valor]
1.2. Calcule o módulo da força centrípeta que actua no Jorge enquanto percorre o troço
circular do escorrega. [1 valor]
1.3. Qual é a velocidade do Jorge quando atinge a água, no sistema de referência da figura?
[1 valor]
1.4. Suponha que os construtores do escorrega pretendem ajustar a altura h, de modo que
os utilizadores toquem na água a uma distância do final do escorrega que seja o dobro da actual.
Qual deverá ser o novo valor de h para conseguirem este objectivo? Justifique. [1,5 valores]
1.5 Em qual das secções do percurso, incluindo o voo para a água, é maior o módulo da
aceleração do Jorge? Justifique. [1,5 valores]
2. Um piano com massa m = 500 kg está a ser descido com velocidade constante, com a
ajuda de um guindaste, estando o Luís e a Marta a puxá-lo para os lados, de modo a mantê-lo
na vertical. Num determinado instante, a corda do Luís puxa-o para a direita, fazendo um
ângulo de 15 ◦ com a horizontal, sendo o módulo da sua tensão 500 N. Por sua vez, a corda da
Marta puxa-o para a esquerda, fazendo um ângulo de 25 ◦ com a horizontal.
25o
15o
2.1. Apresente o diagrama das forças aplicadas ao piano no instante referido e escreva a
respectiva legenda. Tenha atenção às dimensões relativas dos vectores. [1 valor]
2.2. Qual é o módulo da tensão que a Marta deverá manter na sua corda para que o piano
desça na vertical? [1 valor]
2.3. Qual é o módulo da tensão no cabo de que está suspenso o piano? [1 valor]
3. Um náufrago numa ilha deserta pretende alcançar a fruta que está suspensa de um ramo
elevado de uma árvore. Felizmente, dispõe de uma espingarda de mola, com a qual pode lançar
uma pedra. Todas as pedras da ilha parecem ter massa de 400 g. A constante da mola da
espingarda é k = 1000 N/ m, e a distância de que a mola é comprimida é 30 cm. Despreze a
resistência do ar.
3.1. Nesta situação defina o sistema como constituído pela Terra, pela mola da espingarda
e pela pedra. Identifique todas as formas de energia deste sistema que estão em jogo, desde
que a mola é comprimida até a pedra atingir a altura máxima. [1 valor]
3.2. Qual é o módulo da velocidade da pedra quando deixa de estar em contacto com a mola
da espingarda da espingarda, se esta é disparada na vertical? [1 valor]
3.3. Se a fruta se encontra 15 m acima da posição de partida da pedra, conseguirá o náufrago
fazer cair a fruta, ou terá de procurar outro alimento? [1 valor]
Física I A e D 2006/2007 - Avaliação de Recurso - 23 de Julho de 2007
2.a Parte
Responda aos seguintes dois problemas. Apresente todas as etapas utilizadas para resolver
cada problema, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que
tal seja pedido.
1. Um foguete, com massa 103 kg é disparado na vertical a partir do solo e sobe com aceleração
vertical de módulo constante igual a 20 m/ s2 durante 1 minuto, após o que, tendo-se esgotado o
combustível, o foguete passa a mover-se sujeito apenas à força da gravidade terrestre. Despreze a
resistência do ar, a variação da massa do foguete devido ao consumo do combustível e considere
g = 10 m/ s2 em todos os pontos do percurso do foguete.
1.1. Qual é a altitude do foguete no instante em que se esgota o combustível? [0.5 valores]
1.2. Qual é o valor do módulo da velocidade do foguete no instante em que se esgota o combustível?
[0.5 valores]
1.3. Qual é a altitude máxima atingida pelo foguete? [1 valor]
1.4. Calcule o trabalho realizado pela força gravítica da Terra sobre o foguete, durante o movimento ascensional deste. [1 valor]
1.5. Calcule o tempo total decorrido desde o disparo do foguete até este atingir de novo o solo.
[1 valor]
2. Um corpo, suposto pontual e com massa igual a 10 g, ligado a uma mola em hélice, move-se
com movimento harmónico simples, de amplitude igual a 24 cm e período 4.0 s, ao longo de um eixo
horizontal, em torno do ponto x = 0. No instante t = 0 s a coordenada de posição é x = 24 cm
2.1. Qual é o valor da constante da mola? [1 valor]
2.2. Obtenha a expressão matemática da posição do corpo em função do tempo. [1 valor]
2.3. Calcule o módulo e o sentido da força que actua no corpo no instante t = 0.5 s. [1 valor]
2.4. Calcule o intervalo de tempo mínimo para o corpo se mover da sua posição inicial até ao
ponto de coordenada x = −12 cm. [1 valor]
1
Física I A e D - Avaliação Especial 2006/2007 - 21 de Setembro de 2007
2.a Parte
Responda aos seguintes dois problemas. Apresente todas as etapas utilizadas para resolver cada problema, justificando-as cuidadosamente, e apresente um resultado numérico,
sempre que tal seja pedido. Utilize para o módulo da aceleração de um corpo à superfície
da Terra, resultante da gravidade, g = 10.0 m/ s2 .
1. Um tijolo com massa 28.0 kg está em repouso sobre o tampo de uma mesa, ligado a
um balde vazio, com massa 1.00 kg, através de um fio de massa desprezável que passa por
uma roldana sem atrito (figura 1). O coeficiente de atrito estático entre a mesa e o tijolo é
μe = 0.450 e o coeficiente de atrito cinético entre estes dois corpos é μc = 0.320. Coloca-se
progressivamente areia no balde até que o sistema (tijolo + balde) começa a mover-se.
Figura 1:
1.1. Desenhe o diagrama de forças aplicadas ao tijolo, quando este está em repouso, e
identifique-as. Tenha em atenção a dimensão relativa dos vectores. [1 valor]
1.2. Identifique os corpos em que se exercem as forças de reacção correspondentes às forças
indicadas na resposta à questão 1.1. [1 valor]
1.3. Calcule o valor da massa de areia existente no balde, no instante em que o sistema
inicia o movimento.[1 valor]
1.4. Calcule o módulo da aceleração do sistema, após se ter iniciado o movimento. [1 valor]
1
2. A figura 2 mostra um dispositivo familiar nos parques de diversões. O jogador deve
lançar o martelo A (com massa mA = 4.00 kg) de modo que o módulo da velocidade deste no
impacto com a bigorna B seja de 8.00 m/ s, para que o corpo C vá tocar na campainha D (e
faça "ding"). Despreze a massa da bigorna e todas as forças de atrito durante o movimento do
corpo C.
Nestas condições, a mola que está presa à bigorna comprime-se de 2.00 cm. O valor da
constante da mola é k = 1.20 × 105 N/ m. O corpo C (com massa mC = 1.20 kg) sobe a uma
altura de 2.00 m, até bater na campainha. Suponha que o corpo atinge a campainha com
velocidade nula.
D
ding!!!
2.00 m
A
C
B
Figura 2:
2.1. Calcule o módulo da velocidade do corpo C no instante em que deixa a bigorna. [1
valor]
2.2. Calcule a energia potencial do sistema " corpo C + Terra" no instante em que o
corpo atinge a campainha, considerando nula essa energia quando o corpo C está na posição
inicial. [0.5 valor]
2.3. Calcule o valor máximo da energia potencial acumulada na mola depois de a bigorna
ter sido atingida pelo martelo. [0.5 valor]
2.4. As forças que intervêm na colisão do martelo com a bigorna não são conservativas.
Justifique esta afirmação por meio de cálculos apropriados. [2 valores]. Sugestão: Calcule a a
energia mecânica do sistema "corpo C + mola + martelo + Terra" antes e depois da referida
colisão. Suponha que o martelo fica imóvel imediatamente após a colisão com a bigorna.
2
Física I 2007/2008 - 1.o Teste - 12 de Novembro de 2007
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver,
justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido.
Sempre que necessário, utilize para o módulo da aceleração resultante da gravidade o valor
g = 10.0 m/ s2 .
Uma esfera encontra-se na base de um plano inclinado de altura H = 0.75 m e L = 1 m de
comprimento como mostra a figura 1. Após ter sido comunicada à esfera uma velocidade inicial de
módulo v0 na direcção perpendicular à linha de base do plano, ela desloca-se ao longo do plano até
uma determinada altura, voltando então a descer. Despreze o atrito entre a esfera e o plano inclinado
e o movimento de rotação da esfera.
Figura 1
1. Passe para a sua folha de prova, os sistemas de eixos coordenados da figura 2.
Figura 2
Utilize esses sistemas de eixos para fazer um esboço dos gráficos da velocidade em função do
tempo e da aceleração em função do tempo, para o movimento da bola desde o momento em que
é largada até imediatamente antes de chegar à base do plano. Considere como positivos os valores
destas grandezas quando os correspondentes vectores apontam para cima. [2 valores]
1
2. Se o módulo da velocidade inicial da esfera é 2, 0 m/ s, calcule a distância total percorrida pela
esfera até parar. Apresente todas as etapas de resolução. [3 valores]
3. A esfera é agora lançada de um ponto à distância d = 0.90 m da base do plano, com velocidade
de módulo 1.5 m/ s e direcção paralela à base (figura 3). Calcule as coordenadas do ponto em que a
esfera atinge a base do plano, utilizando o sistema de referência da figura. Apresente todas as etapas
de resolução [3 valores]
Figura 3.
Fórmulas fornecidas:
Equação da posição em função do tempo para o movimento uniformemente acelerado, com aceleração a:
1
r = r0 + v0 t + at2 .
2
Equação da velocidade em função do tempo para o movimento uniformemente acelerado, com
aceleração a:
v = v0 + at
Nestas equações, r0 e v0 são os vectores posição e velocidade iniciais, respectivamente.
2
Física I 2007/2008 - 1.o Teste - 19 de Dezembro de 2007
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o
resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre
que tal seja pedido. Utilize para o módulo da aceleração resultante da gravidade o
valor g = 10.0 m/ s2 .
Neste problema despreze as forças de resistência do ar e das peças móveis internas do automóvel, bem como as dimensões deste último.
Um automóvel com massa 1.50 × 103 kg está a aproximar-se de uma pequena elevação
(ver figura) com velocidade de módulo 40.0 km/ h, quando de repente fica sem gasolina.
30
A
o
5.00 m
5.00 m
20o
B
a) Conseguirá o automóvel atingir o topo da elevação? Em caso afirmativo, qual
o módulo da velocidade do automóvel nesse ponto. Justifique cuidadosamente a sua
resposta. [2 valores]
b) Suponha que o carro atingiu o topo da elevação e continua a mover-se descendo
pelo lado oposto.
Defina, para o caso presente, o sistema físico que deverá utilizar para calcular a variação
da energia potencial, que deverá identificar, associada à interacção entre os corpos que
constituem esse sistema.Calcule então a variação dessa energia potencial no movimento
do automóvel entre as posições A e B. [2 valores]
c) Após passar a posição B, o condutor, avistando um obstáculo na estrada, trava a
fundo, bloqueando as rodas, e o automóvel atinge o repouso tendo-se deslocado 30.0 m
durante a travagem. Qual é o coeficiente de atrito cinético entre os pneus e o solo na zona
de travagem? Justifique as diferentes etapas do seu cálculo. [3 valores]
d) O coeficiente de atrito estático entre os pneus e o solo é maior do que o correspondente coeficiente de atrito cinético. Qual seria o procedimento correcto que o condutor
devia ter seguido, no caso da alínea anterior para conseguir levar o automóvel ao repouso
no menor espaço possível? Não se esqueça de justificar a resposta. [1 valor]
1
Física I 2007/2008 - 1.o Teste - 20 de Dezembro de 2007
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o
resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre
que tal seja pedido. U tilize para o módulo da aceleração resultante da gravidade o
valor g = 10.0 m/ s2 .
Após ter caído 370 m sem o paraquedas abrir, o piloto de um avião foi travado finalmente por um banco de neve, sofrendo apenas ferimentos ligeiros. A queda provocou na
neve uma cratera com 1.1 m de profundidade. Suponha que a massa do piloto é de 80 kg
e que o módulo da sua velocidade terminal era 50 m/ s.
a) Defina, para o caso presente, o sistema físico que deverá utilizar para calcular
a variação da energia potencial, que deverá identificar, associada à interacção entre os
corpos que constituem esse sistema. Calcule então a variação dessa energia potencial no
movimento do piloto desde que saíu do avião até tocar na neve [2 valores]
b) Calcule o trabalho efectuado sobre o piloto pela resistência do ar durante a queda.[3
valores]
c) Obtenha o impulso (módulo, direcção e sentido) da força exercida sobre o piloto
pela neve neste processo. [2 valores]
d) Calcule o trabalho efectuado pela neve sobre o piloto para o levar ao repouso. [1
valor]
1
Física I 2007/2008 - 2.o Teste - 24 de Janeiro de 2008
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver,
justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido.
Utilize para o módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
Uma máquina de Atwood é constituída por dois corpos de massas m1 = 8.8 kg e m2 = 7.0 kg
ligados por um fio de massa desprezável através de uma roldana que pode rodar sem atrito em
torno de um eixo fixo. Considere a roldana como um cilindro sólido de raio R = 0.50 m e massa
M = 0.80 kg. Despreze o atrito no eixo da roldana.
a) Calcule o módulo da aceleração dos corpos 1 e 2; [6 valores]
b) Determine a aceleração angular da roldana, indicando o respectivo módulo, direcção e sentido..
[2 valores]
Justifique cuidadosamente as suas respostas.
Sugestão: O momento de inércia de um cilindro sólido de raio R e massa M, em relação ao eixo
1
principal é I = MR2 .
2
R
1
2
1
Física I 2007/2008 - Recurso - 9 de Fevereiro de 2008
2.a Parte
Na resposta aos seguinte problemas, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que
tal seja pedido. Utilize para o módulo da aceleração resultante da gravidade o valor
g = 10.0 m/ s2 .
1.
Um corpo pontual com massa m = 0.1 kg desliza sem atrito a partir do repouso (em
A), sobre um plano inclinado AB e, a partir do ponto B, sobre uma calha circular até ao ponto
D, como a figura 1 indica. O centro da calha circular é o ponto P e o raio da calha é a = 0.5 m.
A altura do plano inclinado é h = 1.5 m e o plano faz com a horizontal um ângulo α = 37◦ . O
ponto C é o ponto médio do arco BD (PC tem, consequentemente, a direcção vertical e BP é
perpendicular ao plano inclinado AB).
Figure 1:
a) Indique, representando-as graficamente, as forças que actuam no corpo em questão
quando ele se encontra no ponto A e quando passa no ponto C. Não esqueça os comprimentos
relativos de vectores e faça uma legenda. [1 valor]
b) Determine o módulo do vector velocidade do corpo no ponto C, e indique a respectiva
direcção e sentido. [1 valor]
c) Calcule o momento angular do corpo quando passa na posição B, em relação ao ponto A
e em relação ao ponto P, indicando, em cada caso, o módulo, a direcção e o sentido. [1 valor]
d) Há conservação do momento angular do corpo em relação ao ponto P durante o percurso
BD? Justifique em termos físicos . [1 valor]
1
2. Dois corpos com massas, respectivamente m1 = 0.1 kg e m2 = 0.2 kg, que se movem
sem atrito sobre um plano horizontal com velocidades, respectivamente v1 = 0.6 ux ( m/ s) e
v2 = −0.6 ux − 0.2 uy ( m/ s), colidem.
a) Calcule a velocidade do centro de massa do sistema antes do choque, no sistema de
referência em que estão expressas as velocidades dos dois corpos. [1 valor]
b) A velocidade do centro de massa do sistema é alterada pelo choque? Dê uma justificação
física para a sua resposta. [1 valor]
c) Depois da colisão, a partícula de massa m2 possui velocidade com módulo 2 m/ s e desloca3
se segundo uma direcção que faz com o eixo dos x um ângulo α = π rad. Calcule a velocidade
4
v10 da partícula de massa m1 depois do choque. [1 valor]
d) Verifique que o momento linear total do sistema das duas massas é nulo no referencial
do centro de massa. [1 valor]
Fórmulas que podem ser úteis:
1. Equação da posição, r, em função do tempo, t, para o movimento uniformemente acelerado, com aceleração a:
1
r = r0 + v0 t + at2 .
2
2. Equação da velocidade, v, em função do tempo, t, para o movimento uniformemente
acelerado, com aceleração a:
v = v0 + at
Nas equações 1. e 2., r0 e v0 são os vectores posição e velocidade iniciais, respectivamente.
3. Momento da força F em relação à origem de um sistema de coordenadas:
τ =r×F
4. Momento angular de um corpo em relação à origem de um sistema de coordenadas:
L=r×p
Nas equações 3. e 4., r é o vector posição do ponto de aplicação da força no sistema
considerado
Na equação 4., p é o momento linear do corpo.
2
Física I 2007/2008 - 1.o Teste - 26 de Março de 2008
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o
resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre
que tal seja pedido.
O João e a Maria são dois jovens apaixonados pela mecânica. Construiram cada um
o seu veículo automóvel, uma espécie de kart. Pretendem agora competir um com o
outro numa pista linear e horizontal, na propriedade da família de um deles. O sistema
de referência utilizado consiste num eixo horizontal com origem no ponto de partida e o
sentido do deslocamento dos carros durante a corrida.
META
x
0
a) O carro do João deslocou-se inicialmente com a aceleração constante de valor máximo que o motor permitiu mas, após t1 = 20.0 s, quando o módulo da sua velocidade era
v1J = 10.0 m/ s, o motor avariou-se e o carro passou a deslocar-se com aceleração constante igual a a2J = −5.00 × 10−2 m/ s2 , devido aos atritos. O tempo total necessário para
o João atingir a meta foi de tTotJ = 160 s, contado desde a partida. Qual é o comprimento
da pista? [5 Valores]
b) A Maria preferiu ser mais cautelosa. No seu primeiro percurso após a partida, de
comprimento 1 = 200 m, o módulo da aceleração do seu carro foi a1M = 0.100 m/ s2 , após
o que manteve a velocidade constante, durante 128 s até atingir a meta. Quem é que
ganhou a corrida?
1
Física I 2007/2008 - 2.o Teste - 7 de Maio de 2008
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver,
justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja
pedido. Sempre que necessário, utilize para o módulo da aceleração resultante da gravidade
o valor g = 10.0 m/ s2 .
O João e a Maria continuam apaixonados pela Física, competindo agora na construção de
foguetes, lançados em trajectórias verticais de forma a atingirem a maior altitude possível. A
massa do foguete construído pelo João é mJ = 5.0 kg, enquanto que a massa do foguete construído
pela Maria é mM = 6.0 kg.
Partindo do repouso, cada foguete deslocou-se com aceleração constante (de módulos
aJ = 6.0 m/ s2 e aM = 4.0 m/ s2 , respectivamente, para os foguetes do João e da Maria) até
se esgotar o combustível, quando o foguete se encontrava à altura hi (hJ para o foguete do João e
hM para o foguete da Maria). A partir desse ponto o foguete passou a deslocar-se sujeito apenas
à força da gravidade.
Na resolução deste problema despreze a resistência do ar, a variação da massa do foguete
devido ao consumo do combustível e a variação da força da gravidade com a altitude.
a) Apresente os diagramas das forças que actuam num dos foguetes no percurso desde a partida
até atingir a altura hi e no restante percurso até o foguete regressar de novo ao solo. Não se esqueça
das relações aproximadas entre as intensidades das forças e apresente as legendas dos diagramas.
[1 valor]
b) O trabalho realizado pela força resultante que actuou no foguete do João durante o percurso
até atingir a altura hJ foi WJ = 8.1×104 J, enquanto que o trabalho realizado pela força resultante
que actuou no foguete da Maria durante o percurso até atingir a altura hM foi WM = 7.7 × 104 J.
Qual dos foguetes se encontrava mais longe do solo quando o respectivo combustível se esgotou?
[4 valores].
c) Calcule a altura máxima atingida por cada um dos foguetes e, como consequência, identifique
o vencedor da competição. [3 valores]
1
Física I 2007/2008 - 3.o Teste - 18 de Junho de 2008
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver,
justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido.
Sempre que necessário, utilize para o módulo da aceleração resultante da gravidade o valor
g = 10.0 m/ s2 .
Um vagão de carga vazio, com massa 1000 kg, desloca-se com velocidade de módulo 0.90 m/ s
sobre uma linha férrea plana e rectilínea e choca com outro vagão carregado, que está em repouso
mas com os travões desengatados e possui massa total de 2000 kg.
1. Se os dois vagões permanecem juntos após a colisão, determine o módulo da sua velocidade
comum. [3 valores]
2. Calcule a variação da energia cinética que resulta da colisão. [2 valores]
3. Com que velocidade (módulo e sentido) se deveria deslocar o vagão carregado, antes da colisão,
para que ambos ficassem em repouso após a colisão? [3 valores]
Fórmula fornecida para a 1.a parte do teste:
1
Momento de inércia de um disco de massa M e raio R em relação ao eixo de simetria: I = MR2 .
2
1
Física I 2007/2008 - Avaliação de Recurso - 9 de Julho de 2008
2.a Parte - Versão a
Nas suas respostas aos seguintes dois problemas, apresente todas as etapas utilizadas
para os resolver, justificando-as cuidadosamente, e apresente um resultado numérico,
sempre que tal seja pedido. A ausência de uma justificação aceitável na resolução
implica a perda de 25% do valor atribuído à questão. Sempre que necessário, utilize
para o módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
1. O "bungee jumping" é um desporto radical em que destemidos atletas saltam da borda de
uma ponte com um cabo flexível amarrado a um dos pés, permitindo amortecer a queda.
Na situação a que se refere este problema, o comprimento normal do cabo (quando a sua tensão
é nula) é L = 12 m. A atleta, de massa m = 60 kg salta de um trampolim na borda da ponte
com velocidade inicial de direcção vertical, sentido para cima e módulo v0 = 5.0 m/ s. Considere a
atleta como uma massa pontual, suponha que o movimento é unidimensional, na vertical, despreze
a resistência do ar e a massa do cabo.
1.1. Qual é o módulo, direcção e sentido da aceleração da atleta no instante em que atinge a
altura máxima? [1 valor]
1.2. Calcule a distância a que se encontra a atleta do ponto de partida no instante em que atinge
a altura máxima. [0.5 valores]
1.3. Se a distância total de que cai a atleta, desde o ponto de partida é 31 m, calcule a constante
k do cabo, supondo que a lei da Hooke lhe é aplicável. [2 valores]
1.4. Qual é valor do módulo da aceleração da atleta quando esta se encontra no ponto mais baixo
da queda? Se não resolveu a alínea anterior, utilize k = 100 N/ m. [1 valor]
1.5. Se, após a queda, a atleta ficar a oscilar na extremidade do cabo, qual é a frequência angular
desse movimento? Se não resolveu a alínea 1.3, utilize k = 100 N/ m. [0.5 valores]
1
2. Uma vara de massa desprezável e comprimento 1.20 m tem em cada extremidade uma esfera
muito pequena com massa de 1.00 kg. A vara roda no plano horizontal, em torno do seu ponto médio,
no sentido directo, quando observada de uma posição acima do plano de rotação. Num determinado
instante, verifica-se que a velocidade angular da vara tem módulo ω 0 = 2.45 × 102 rad/ s. Devido
ao atrito com o eixo, a vara chega ao repouso após um intervalo de tempo ∆t = 32.0 s. Calcule,
supondo que o momento de força de atrito é constante:
2.1. A aceleração angular da vara (direcção, sentido e módulo). [1 valor]
2.2. O momento de inércia do sistema constituido pela vara e as duas esferas, supostas pontuais,
em relação ao ponto médio da vara. [1 valor]
2.3. O momento de força de atrito que origina a aceleração da vara (direcção, sentido e módulo).
Se não resolveu a alínea 2.1, utilize como módulo da aceleração angular do sistema 8.00 rad/ s2 . [1
valor]
2.4. O trabalho efectuado pela força de atrito durante o intervalo de tempo ∆t. [1 valor]
2.5. O número de revoluções completas efectuadas pela vara durante esse intervalo de tempo. [1
valor]
2
Física I 2007/2008 - Avaliação da Época Especial - 18 de Setembro de 2008
2.a Parte
Nas suas respostas aos seguintes dois problemas, apresente todas as etapas utilizadas
para os resolver, justificando-as cuidadosamente, e apresente um resultado numérico,
sempre que tal seja pedido. A ausência de uma justificação aceitável na resolução
implica a perda de 25% do valor atribuído à questão. Sempre que necessário, utilize
para o módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
1. Um foguete, com massa 1.0 × 103 kg é disparado na vertical a partir do solo e sobe com
aceleração vertical de módulo constante igual a 20 m/ s2 durante 60 s, após o que, tendo-se esgotado
o combustível, o foguete passa a mover-se sujeito apenas à força da gravidade terrestre. Despreze
a resistência do ar, a variação da massa do foguete devido ao consumo do combustível e considere
g = 10 m/ s2 em todos os pontos do percurso do foguete.
1.1. Qual é a altitude do foguete no instante em que se esgota o combustível? [1 valor]
1.2. Qual é o valor do módulo da velocidade do foguete no instante em que se esgota o combustível?
[1 valor]
1.3. Qual é a altitude máxima atingida pelo foguete? [1 valor]
1.4. Calcule o trabalho realizado pela força gravítica da Terra sobre o foguete, durante o movimento ascensional deste. [1 valor]
1.5. Calcule o tempo total decorrido desde o disparo do foguete até este atingir de novo o solo.
[1 valor]
2. Uma escada uniforme, com comprimento L = 5.00 m, e peso com módulo 200 N está encostada
a uma parede vertical sem atrito, com a extremidade inferior à distância D = 3.00 m da parede. O
coeficiente de atrito estático entre a escada e o chão é μe = 0.400. Um homem com o peso de módulo
800 N sobe lentamente a escada.
L
D
2.1. Apresente um diagrama das forças aplicadas à escada, bem como a respectiva legenda,
identificando cada uma das forças. (Sugestão: no diagrama desenhe a escada de perfil).[1 valor]
2.2. Qual é o valor máximo do módulo da força de atrito estático que o chão pode exercer sobre
a escada? [1 valor]
2.3. Apresente as expressões das condições de equilíbrio estático da escada. Não se esqueça de
indicar o sistema de referência que utilizar. [1 valor]
2.4. Tendo o homem percorrido 2.50 m ao longo da escada, qual é o módulo da força de atrito
exercida pelo chão na escada nesse instante? [2 valores]
1
Física I 2008/2009 - 1.o Teste - 26 de Novembro de 2008
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver,
justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido.
Sempre que necessário, utilize para o módulo da aceleração resultante da gravidade o valor
g = 10.0 m/ s2 .
O corpo 1, de massa m1 = 1.00 kg, desloca-se sobre uma rampa com atrito, partindo do repouso
no ponto A, de altura h = 3.00 m até ao ponto B, na base da rampa, continuando a deslizar, agora sem
atrito, sobre um plano horizontal, até colidir, elasticamente, com o corpo 2, de massa m2 = 1.00 kg,
que está em repouso no ponto C. Em seguida, o corpo 2 embate numa mola elástica horizontal, cuja
constante é k = 200 N/ m. O coeficiente de atrito cinético entre as superfícies da rampa e do corpo
1 é μc = 0.250. Despreze as dimensões dos corpos 1 e 2 e a massa da mola.
A
1
h
60º
2
B
C
1. Desenhe o diagrama das forças que actuam no corpo 1 enquanto este desce a rampa, fazendo
a respectiva legenda. Tenha em atenção o tamanho relativo dos vectores[1 valor]
2. Determine a intensidade da força de atrito exercida sobre o corpo 1 enquanto este desce a
rampa.[1,5 valores]
3. Calcule o módulo da velocidade do corpo 1 quanto atinge a base da rampa. [2 valores]
Se não resolveu a questão 2., utilize para a intensidade da força de atrito fc = 1.45 N
4. A partir das equações que exprimem a conservação do momento linear numa colisão unidimensional e a conservação da energia cinética total numa colisão elástica, deduza a expressão da
velocidade do corpo 2 imediatamente após a colisão com o corpo 1.
Tenha em conta o facto de o corpos possuiram massas iguais e o corpo 2 estar em repouso
imediatamente antes da colisão.[2 valores]
5. Calcule a distância de que é comprimida a mola como consequência do embate do corpo 2.
[1,5 valores]
Se não resolveu a questão 4., utilize para módulo da velocidade do corpo 2, imediatamente antes de
atingir a mola, o valor v2 = 7.00 m/ s.
1
Física I 2008/2009 - 2.o Teste - 26 de Janeiro de 2009
2.a Parte
Na resposta ao seguinte problema, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido. Sempre que necessário, utilize para o
módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
Uma corda de massa desprezável enrolada num cilindro suspende um corpo maciço sobre um poço com água. A
massa do corpo é de 1.0 kg, a massa do cilindro é 3.0 kg e o raio deste último é de 10 cm.
A
1. Qual é o módulo da força de menor intensidade que é necessário exercer no ponto A da manivela, que dista 20 cm
do eixo do cilindro, para manter o sistema cilindro+corpo em repouso? [2 valores]
2. Quando a força deixar de ser exercida na manivela, o corpo vai deslocar-se verticalmente até atingir à água do
poço. Calcule o módulo da aceleração angular do cilindro, em torno do seu eixo principal, durante o movimento
de descida do corpo. Despreze todas as forças de resistência e a massa da manivela. [2 valores]
3. O corpo atinge a água 5 s após se ter iniciado o movimento. Calcule o módulo da velocidade do corpo imediatamente antes de atingir a água. Se não resolveu a alínea anterior, utilize para módulo da aceleração angular do
cilindro o valor 15.0 rad/ s2 . [2 valores]
4. Após o corpo chegar à água, fica em repouso com 2/3 do seu volume abaixo da superfície livre da água. Qual é
a massa volúmica deste corpo? [2 valores]
Fórmulas e dados fornecidos:
1
Momento de inércia de um cilindro de raio R e massa M , em relação ao eixo principal: M R2
2
1
Equação de Bernoulli: P + ρv 2 + ρgy = constante
2
P → pressão; ρ → massa volúmica do fluido; v → velocidade do fluido; y → altura do ponto em que a
pressão e a velocidade do fluido têm os valores P e v.
Massa volúmica da água: 1.00 × 103 kg/ m3
1
Física I 2008/2009 - Avaliação de Recurso - 9 de Fevereiro de 2009
2.a Parte
Na resposta aos seguintes problemas, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido. Sempre que necessário, utilize para o
módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
I
Um rapaz, com massa M = 60.0 kg, está a patinar num lago gelado quando vê um carrinho de bebé, com massa
total m = 8.00 kg que desliza, com velocidade constante de módulo igual a v = 4.00 m/ s, em direcção a um buraco no
gelo. O rapaz, deslocando-se, também com velocidade constante de módulo igual a V = 12.0 m/ s, na mesma direcção
da trajectória do carrinho, alcança este último agarrando-o pela pega.
1. Calcule o módulo da velocidade do conjunto rapaz+carrinho, imediatamente após o rapaz ter agarrado o carrinho.
[1 valor]
2. Imediatamente após ter alcançado o carrinho, o rapaz coloca os patins perpendicularmente à trajectória, originando uma força de atrito entre os patins e o gelo. O coeficiente de atrito cinético entre os patins e o gelo é
μc = 0.350. Se no instante em que o rapaz alcançou o carrinho, este estava à distância de 20 m do buraco no
gelo, o rapaz consegue evitar que o carro caia no buraco? Justifique cuidadosamentea sua resposta. [2 valores]
Se não resolveu a alínea anterior, utilize para módulo da velocidade do conjunto v = 10.0 m/ s.
3. Calcule o trabalho realizado pela força de atrito entre o gelo e os patins até o conjunto rapaz+carrinho atingir
o repouso ou cair no buraco no gelo. [1 valor].
Se não resolveu a alínea anterior, utilize para módulo do deslocamento do conjunto o valor
= 20 m
II
Um satélite lunar, com massa ms = 20.0 kg encontra-se numa órbita circular em torno da Lua, à altitude h =
20.0 km.
1. Qual é o módulo da força exercida no satélite durante o movimento orbital? [1 valor]
2. Obtenha o módulo da velocidade orbital do satélite. [1 valor]
3. Qual é o valor da energia total do sistema satélite+Lua na situação descrita neste problema? [1 valor]
4. Qual é o valor do módulo da velocidade mínima adicional que deverá ser fornecida ao satélite para que este se
afaste para uma distância infinita da Lua? [1 valor]
1
Nesta prova, os vectores unitários segundo os eixos cartesianos x, y e z são denotados, respectivamente, por i, j e
k.
Fórmulas e dados fornecidos:
Constante da gravitação universal: G = 6.67 × 10−11 m3 kg−1 s−2
Massa da Lua: ML = 7.35 × 1022 kg.
Diâmetro da Lua: DL = 3.476 × 103 km
1
Equação de Bernoulli: P + ρv 2 + ρgy = constante
2
P → pressão; ρ → massa volúmica do fluido; v → velocidade do fluido; y → altura do ponto em que a
pressão e a velocidade do fluido têm os valores P e v.
2
Física I 2008/2009 - Avaliação Normal - 23 de Junho de 2009
2.a Parte
A resolução da segunda parte da avaliação deverá ser efectuada no conjunto de 4 folhas que lhe foi fornecido.
Na resposta aos seguintes problemas, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido. Sempre que necessário, utilize para o
módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
1. Um camião está a puxar um reboque ao longo de uma estrada horizontal, como mostra a figura. A massa do
camião é mC = 1.00 × 104 kg e a do reboque é mR = 3.00 × 104 kg. O movimento dos dois veículos é rectilíneo,
com aceleração de módulo a = 0.700 m/ s2 . Despreze as forças retardadoras resultantes dos atritos internos dos
veículos e da resistência do ar.
(a) Represente, em dois diagramas separados, as forças aplicadas ao camião e as forças aplicadas ao reboque.
Respeite, de forma aproximada, a proporcionalidade entre as intensidades das diversas forças e não esqueça
as respectiva legendas. [1 valor]
(b) Identifique um par de forças de acção e reacção entre as forças representadas nos diagramas que desenhou;
[0,5 valores]
(c) Determine o valor do módulo da força exercida pelo reboque no camião; [1,5 valores]
(d) Obtenha o módulo da força que provoca o movimento do sistema constituído pelo camião e pelo reboque.
[1 valor]
2. Uma roda de polir, com a geometria de um disco sólido uniforme, tem de raio 7.00 cm e de massa 2.00 kg. A
roda parte do repouso e acelera uniformemente, sob a acção de momento de uma força constante, em relação
ao eixo de rotação, com módulo igual 0.600 N m. Este momento de força é exercido por um motor durante um
determinado intervalo de tempo, após o que o motor é desligado e o movimento de rotação da roda passa a ser
uniforme.
(a) Qual é o intervalo de tempo que decorre até a roda alcançar a velocidade angular final de 1200 rotações/min?
[2 valores]
(b) Calcule o número revoluções completas ocorridas enquanto durou a aceleração da roda. [1 valor]
(c) Determine o módulo da velocidade linear de um ponto na periferia do disco, após este ter atingido o regime
de rotação constante. [1 valor]
Sugestão: Considere a roda de polir como um cilindro homogéneo. O momento de inércia de um cilindro
1
homogéneo de massa M e raio R, em relação ao seu eixo de simetria é I = M R2 .
2
1
Física I 2008/2009 - Avaliação de Recurso -14 de Julho de 2009
2.a Parte
A resolução da segunda parte da avaliação deverá ser efectuada no conjunto de 4 folhas que lhe foi fornecido.
Na resposta aos seguintes problemas, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido. Sempre que necessário, utilize para o
módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
1. Dois corpos, A e B, com massas mA = 15.0 kg e mB = 20.0 kg, respectivamente, encontram-se ligados, conforme
se mostra na figura, por um fio de massa desprezável que passa por uma roldana de raio 0.250 m e momento
de inércia I, em relação ao seu eixo. O corpo A sobe o plano inclinado com aceleração constante com módulo
2.00 m/ s2 . Não existe atrito entre o corpo A e o plano. O ângulo que o plano inclinado faz com a horizontal é 37o .
(a) Desenhe os diagramas de forças aplicadas em cada um dos corpos e na roldana, acompanhados das respectivas legendas . Tenha em atenção a intensidade relativa das forças representadas. [1 valor]
(b) Determine o módulo da tensões do fio em cada um dos lados da roldana. [1 valor]
(c) Calcule o valor do momento de inércia da roldana, relativamente ao seu eixo de rotação. [1 valor]:
(d) Qual deveria ser o módulo da força de atrito cinético entre as superfícies do corpo A e do plano inclinado
para que o módulo da aceleração do corpo A fosse nula? [1 valor]
2. Um satélite com massa de 30 kg encontra-se numa órbita circular a 200 km, acima da superfície da Lua.
(a) Qual é o módulo da velocidade orbital do satélite? [1 valor]
(b) Apresente num esquema simples a direcção e sentido do momento angular do satélite em relação ao centro
da Lua e calcule o módulo desse vector. [1 valor]
Sugestão: Não se esquema de indicar no seu esquema o sentido do movimento do satélite na sua órbita
circular
(c) Em determinado instante, um pequeno objecto, com 1.00 kg de massa é ejectado do satélite na direcção e
sentido da Lua. Calcule:
i. O trabalho realizado pela força gravítica da Lua sobre o objecto desde que este deixa o satélite até
atingir a superfície lunar. [1 valor]
ii. A velocidade do objecto ejectado ao atingir a superfície da Lua. Suponha que o módulo da velocidade
inicial do objecto é igual ao da velocidade do satélite. [1 valor]
Massa da Lua: ML = 7.36 × 1022 kg
Raio médio da Lua: RL = 1.74 × 103 km
Constante Universal da Gravitação: G = 6.67 × 10−11 N m2 kg−2 .
1
Física I - Avaliação de Época Especial 2008/2009 - 7 de Setembro de 2009
2.a Parte
A resolução da segunda parte da avaliação deverá ser efectuada no conjunto de 4 folhas que lhe foi fornecido.
Na resposta aos seguintes problemas, apresente todas as etapas utilizadas para o resolver, justificando-as cuidadosamente, e apresente um resultado numérico, sempre que tal seja pedido. Sempre que necessário, utilize para o
módulo da aceleração resultante da gravidade o valor g = 10.0 m/ s2 .
1. Três blocos com massas, respectivamente, m1 , m2 e m3 , encontram-se em repouso, em contacto uns com os outros
sobre uma superfície horizontal sem atrito¯ conforme
mostra figura. A partir de um determinado instante, uma
¯
→
−
¯ ¯
força horizontal constante F , de módulo ¯F ¯ = 18.0 N, é aplicada ao corpo de massa m1 . Sendo m1 = 2.00 kg,
m2 = 3.00 kg, m3 = 4.00 kg, determine, nesta situação:
(a) O módulo da aceleração dos blocos; [1 valor]
(b) Os módulos das forças resultantes que actuam em cada um dos blocos; [1 valor]
(c) O módulo do momento linear do corpo de massa m2 após terem decorrido 4 s desde que a força F começou
a ser exercida; [1 valor]
(d) O trabalho realizado, num deslocamento de 2 m, pela força que o bloco de massa m3 exerce no bloco de
massa m2 . [1 valor]
m1
F
m2
m3
2. Quatro partículas, com massas 4.0 kg, 2.0 kg, 2.0 kg e 3.0 kg, encontram-se localizadas nos vértices de um rectângulo, ligadas por barras rígidas de massa desprezável conforme se mostra na figura. Considere que a origem
do sistema de eixos, O, coincide com o centro do rectângulo. Se o sistema girar no plano xy em torno do eixo
dos z, com velocidade angular constante e igual a 6.00 rad/s, e no sentido indicado na figura, calcule:
(a) O momento de inércia do sistema em relação ao eixo dos z. [1 valor]
(b) A energia cinética de rotação do sistema. [1 valor]
(c) Em determinado instante é aplicada uma força constante numa das partículas, levando o sistema ao repouso
em 3 s. [1 valor]
i. Indique, justificando a direcção e o sentido do momento dessa força em relação ao ponto O.
ii. Calcule o módulo desse momento de força. [1 valor]
y
4.00 kg
2.00 kg
sentido da
rotação
6m
O
x
4m
2.00 kg
1
3.00 kg