Relatório_TCC_T mann_2012_Versão_final

UNIJUÍ – Universidade Regional do Noroeste do Estado do Rio grande do Sul
Curso de Engenharia Mecânica – Campus Panambi
TIAGO RAFAEL WEHRMANN
DIMENSIONAMENTO DE UM MECANISMO PANTOGRÁFICO UTILIZANDO
MÉTODO ANALÍTICO E ELEMENTOS FINITOS
Panambi
2012
TIAGO RAFAEL WEHRMANN
DIMENSIONAMENTO DE UM MECANISMO PANTOGRÁFICO UTILIZANDO
MÉTODO ANALÍTICO E ELEMENTOS FINITOS
Trabalho de conclusão do curso apresentado
para
banca
Engenharia
avaliadora
Mecânica
do
da
curso
de
Universidade
Regional do Noroeste do Estado do Rio
Grande do Sul – UNIJUÍ, como requisito
parcial
para
a
obtenção
Engenheiro Mecânico.
Orientador : Roger Schildt Hoffmann , Msc. Eng
Panambi
2012
do
titulo
de
TIAGO RAFAEL WEHRMANN
DIMENSIONAMENTO DE UM MECANISMO PANTOGRÁFICO UTILIZANDO
MÉTODO ANALÍTICO E ELEMENTOS FINITOS
Trabalho de conclusão da Graduação em Engenharia Mecânica para obtenção do
titulo de Engenheiro Mecânico, na Universidade Regional do Noroeste do Estado do
Rio Grande do Sul – UNIJUÍ.
Banca Examinadora:
............................................................................................................
Prof. Msc. Eng. Roger Schildt Hoffmann –Dceeng (Orientador)
............................................................................................................
Prof. Dr. Eng. Antonio Carlos Valdiero - Dceeng
Panambi,.....de .......................de..........
AGRADECIMENTOS
Agradeço à minha família, em especial aos meus
pais, Reinhard e Temia, minha esposa Cristine e meu filho
Kauã por todo amor, apoio e incentivo que dedicaram a
mim.
Agradeço
ao
meu
professor,
Roger
Schildt
Hoffmann, por acreditar no meu esforço e trabalho e
também por me transmitir sua experiência e seus
conhecimentos nas áreas afins deste trabalho.
RESUMO
Este trabalho relata o dimensionamento dinâmico de um mecanismo
pantográfico através de cálculos analíticos e numéricos com o objetivo de
dimensionar uma estrutura segura e leve. Os cálculos das forças dinâmicas foram
obtidos através da teoria da estática com incremento de um fator que as
transformam em cargas dinâmicas, os cálculos analíticos foram realizados a partir da
teoria de resistência dos materiais, implementados com o auxílio de uma planilha no
software Excel elaborada para este trabalho e os cálculos numéricos foram
realizados com base no método de elementos finitos implementado no software de
elementos finitos Ansys. Para auxiliar o entendimento do trabalho elabora-se a
revisão bibliográfica de resistência dos materiais clássica e do método dos
elementos finitos, essa expondo o conteúdo de forma breve e de fácil entendimento.
Palavras-chaves: Dimensionamento do mecanismo pantográfico, Dimensionamento
analítico, Dimensionamento por elementos finitos.
ABSTRACT
This paper reports the dynamic design of a pantograph mechanism through
static formulation and analytical and numerical calculations in order to design a safe
structure and light structure. The calculations of the dynamic forces were obtained
through the static theory of an increase of a factor that turn them into dynamic loads,
the analytical calculations were based on the theory of strength of materials,
implemented with the aid of a spreadsheet in Excel software developed for this work
and numerical calculations were performed based on the finite element method
implemented in the finite element software Ansys. To assist the understanding of the
work to prepare a literature review of classical strength of materials and finite element
method,
exposing
the
contents
of
this
brief
and
easy
to
understand.
Keyword: Design of the pantograph mechanism, analytical method, Finite element
method
design....………..…………………………………………………………………...
LISTAS DE FIGURAS
Figura 1: Barra quadrada submetida ao carregamento axial [1] ........................................... 15
Figura 2: Princípio de Saint-Venant [2] ................................................................................ 16
Figura 3: Distribuição de tensão para uma barra retangular com força concentrada [1] ....... 16
Figura 4: Exemplos de geometrias que possuem concentradores de tensão [1] .................. 17
Figura 5: Coeficientes de concentração de tensão para peças tracionadas com furo central
[3] ........................................................................................................................................ 17
Figura 6: Coeficientes de concentração de tensão para peças tracionadas por um eixo no
centro do furo [3].................................................................................................................. 18
Figura 7: Peça submetida à cisalhamento puro [6] .............................................................. 18
Figura 8: Cisalhamento na chapa do suporte (área Ac) [5] ................................................... 19
Figura 9: Peça submetida à cisalhamento e flexão [6] ......................................................... 19
Figura 10: Deformação de uma viga submetida à flexão [1]................................................. 20
Figura 11: Secção da barra submetida à cisalhamento [12] ................................................. 20
Figura 12: Distribuição da tensão de cisalhamento em perfis de secção circular, quadrada e
retangular [1] ....................................................................................................................... 21
Figura 13: Distribuição da tensão de cisalhamento no perfil ‘’I” [1] ....................................... 21
Figura 14: Área de esmagamento [6] ................................................................................... 22
Figura 15: Exemplo de um eixo submetido à torção e flexão [7] .......................................... 23
Figura 16: Distribuição da tensão de cisalhamento devido ao torque [1] .............................. 24
Figura 17: Imagem de uma viga submetida à flexão [12] ..................................................... 25
Figura 18: Diagrama de força cortante [12] .......................................................................... 25
Figura 19: Diagrama de momento fletor [12] ........................................................................ 25
Figura 20: Variáveis para cálculo da inércia [1] ................................................................... 26
Figura 21: Gráfico de Concentração de Tensão [3] .............................................................. 27
Figura 22: Elipse formada pela Eq. de von Mises para um estado plano de tensões [6] ...... 28
Figura 23: Elipses formadas pela Eq. de von Mises para o estado tridimensional [6]........... 29
Figura 24: Comprimento efetivo de flambagem (Lo) [1] ....................................................... 31
Figura 25: Rede de elementos finitos [7] .............................................................................. 35
Figura 26: Círculo com cinco elementos do tipo triângulo [9] ............................................... 36
Figura 27: Dimensões do elemento [9] ................................................................................ 36
Figura 28: Viga prismática em balanço [7] ........................................................................... 39
Figura 29: Deslocamentos e esforços nodais positivos [9] ................................................... 42
Figura 30: Viga dividida em duas partes, possuindo dois elementos e três nós [9] .............. 46
Figura 31: Configuração da matriz de uma viga com mais de um elemento [9].................... 47
Figura 32: Pós-processamento de resultados para visualização [11] ................................... 48
Figura 33: Desenho em perspectiva do mecanismo pantográfico [12] ................................. 49
Figura 34: Desenho em perspectiva da alavanca 01 [12] ..................................................... 50
Figura 35: Desenho em perspectiva da alavanca 02 [12] ..................................................... 51
Figura 36: Mesa elevatória [13]............................................................................................ 52
Figura 37: Push/Pulls [14] .................................................................................................... 52
Figura 38: Movimento do mecanismo pantográfico [12] ....................................................... 53
Figura 39: Fluxograma do dimensionamento analítico do mecanismo [12] .......................... 54
Figura 40: Desenho do mecanismo abaixado com carga no centro de DE [12] ................... 56
Figura 41: Barra BD [12] ...................................................................................................... 57
Figura 42: Barra AE [12] ...................................................................................................... 58
Figura 43: Modelo do mecanismo avaliado no Motion [12] .................................................. 60
Figura 44: Gráfico da força do atuador em relação ao tempo [12] ....................................... 60
Figura 45: Gráfico da força do eixo A em relação ao tempo [12].......................................... 60
Figura 46: Gráfico da força do eixo B em relação ao tempo [12].......................................... 61
Figura 47: Gráfico da força do eixo C em relação ao tempo [12] ......................................... 61
Figura 48: Elevação do pantógrafo x Comprimento do atuador [12]..................................... 63
Figura 49: Força de 1 atuador x comprimento do atuador [12] ............................................. 63
Figura 50: Esbeltez da haste [12] ........................................................................................ 64
Figura 51: Gráfico da tensão versus esbeltez pelo critério de Euler [12] .............................. 65
Figura 52: Gráfico da tensão versus esbeltez pelo critério de vigas curtas e intermediárias
[12] ...................................................................................................................................... 66
Figura 53; Geometria do eixo [12] ........................................................................................ 67
Figura 54: Diagrama de corpo livre do eixo da Figura 53 [12] .............................................. 67
Figura 55; Geometria do eixo [12] ........................................................................................ 72
Figura 56: Diagrama de corpo livre para o eixo da articulação A [12] .................................. 72
Figura 57: Diagrama de corpo livre [12] ............................................................................... 74
Figura 58: Geometria do mancal [12] ................................................................................... 75
Figura 59: Diagrama de corpo livre equivalente [12] ............................................................ 77
Figura 60: Gráfico da variação da reação no eixo B e E, conforme elevação do mecanismo
[12] ...................................................................................................................................... 77
Figura 61: Desenho representativo do eixo de suporte do rolo soldado nos tubos [12] ........ 78
Figura 62: Diagrama de corpo livre [12] ............................................................................... 80
Figura 63: Diagrama de corpo livre da barra AE [12] ........................................................... 83
Figura 64: Diagrama de corpo livre da barra BD [12] ........................................................... 85
Figura 65: Suporte do cilindro [12] ....................................................................................... 86
Figura 66: Fluxograma dos passos das análises em elementos finitos [12] ......................... 90
Figura 67: Resultados da Simulação Numérica da Haste [12] ............................................. 91
Figura 68: Resultados da Simulação Numérica do Atuador [12] .......................................... 92
Figura 69: Condições de contorno do mecanismo pantográfico abaixado [12] ..................... 93
Figura 70: Mapa de tensão do pantógrafo abaixado [12] ..................................................... 94
Figura 71: Mapa de deformações do pantógrafo abaixado [12] ........................................... 94
Figura 72: Mapa de tensões da barra AE (vista superior) [12] ............................................. 95
Figura 73: Mapa de tensões da barra AE (vista inferior) [12] ............................................... 95
Figura 74: Mapa de tensões da barra BD (vista superior) [12] ............................................. 96
Figura 75: Mapa de tensões da barra BD (vista inferior) [12] ............................................... 96
Figura 76: Região de concentração de tensão da barra BD [12] .......................................... 97
Figura 77: Mapa de tensões no suporte do atuador [12] ...................................................... 98
Figura 78: Mapa de tensão no tubo circular [12] .................................................................. 99
Figura 79: Mapa de tensão no tubo circular [12] .................................................................. 99
Figura 80: Mapa de tensão do mancal A [12] .................................................................... 100
Figura 81: Mapa de tensões do mancal A [12] .................................................................. 100
Figura 82: Mapa de tensões no eixo da articulação B e E (pantógrafo abaixado) [12] ....... 101
Figura 83: Mapa de tensões no eixo E para o mecanismo elevado [12] ............................ 102
Figura 84: Mapa de tensões no eixo B para o mecanismo elevado [12] ............................ 102
LISTA DE TABELAS
Tabela 1: Peças que compõem o mecanismo pantográfico [12] .......................................... 49
Tabela 2: Peças que compõem o conjunto alavanca 1 [12] ................................................. 50
Tabela 3: Peças que compõem o conjunto alavanca 2 [12] ................................................. 50
Tabela 4: Características técnicas [12] ................................................................................ 53
Tabela 5: Resultados das reações nos eixos e cilindro [12] ................................................. 59
Tabela 6: Propriedades da haste [12] .................................................................................. 64
Tabela 7: Dados para dimensionamento do eixo C [12] ....................................................... 68
Tabela 8: Dados para dimensionamento da bucha da articulação A [12] ............................. 71
Tabela 9: Dados para dimensionamento do eixo da articulação A [12] ................................ 73
Tabela 10: Dados para dimensionamento do mancal A [12] ................................................ 75
Tabela 11: Dados para dimensionamento do tubo [12] ........................................................ 80
Tabela 12: Dados para dimensionamento das barras [12] ................................................... 82
Tabela 13: Dados para dimensionamento do suporte do atuador [12] ................................. 86
Tabela 14: Resultados do dimensionamento analítico [12] .................................................. 88
13
SUMÁRIO
INTRODUÇÃO .......................................................................................................... 13
1 REVISÃO BIBLIOGRÁFICA .................................................................................. 15
1.1 RESISTÊNCIA DOS MATERIAIS ....................................................................... 15
1.1.1 Carregamento axial ........................................................................................ 15
1.1.2 Tensão de cisalhamento ................................................................................ 18
1.1.3 Tensão de esmagamento............................................................................... 22
1.1.4 Torção ............................................................................................................. 22
1.1.5 Flexão .............................................................................................................. 24
1.1.6 Teoria de falha de von Mises ......................................................................... 27
1.1.7 Tensão admissível ......................................................................................... 29
1.1.8 Flambagem ..................................................................................................... 30
1.2 TEORIA DE ELEMENTOS FINITOS ................................................................... 33
1.2.1 Introdução à teoria de elementos finitos e sua história.............................. 33
1.2.2 Conceito do método de elementos finitos ................................................... 34
1.2.3 Fundamento do método de elementos finitos ............................................. 38
1.2.4 Etapas de uma análise numérica através de um software de MEF............47
2 MECANISMO PANTOGRÁFICO ........................................................................... 49
2.1 PRINCIPAIS COMPONENTES DO MECANISMO PANTOGRÁFICO ................ 49
2.1.1 Componentes que formam o conjunto de alavancas 01............................. 50
2.1.2 Componentes que formam o conjunto de alavancas 02............................. 50
2.2 APLICAÇÕES DO MECANISMO PANTOGRÁFICO .......................................... 51
14
3
DIMENSIONAMENTO
DO
MECANISMO
ATRAVÉS
DE
CÁLCULOS
ANALÍTICOS ............................................................................................................ 54
3.1 DETERMINAÇÃO DA FORÇA DINÂMICA DE ELEVAÇÃO ............................... 55
3.2 CÁLCULO DAS REAÇÕES DO MECANISMO ................................................... 55
3.3 DIMENSIONAMENTO DO ATUADOR ................................................................ 61
3.3.1 Dimensionamento do diâmetro da camisa................................................... 61
3.3.2 Dimensionamento da haste do atuador ....................................................... 62
3.4 DIMENSIONAMENTO DA ARTICULAÇÃO CENTRAL C ................................... 66
3.4.1 Dimensionamento do eixo da articulação C ................................................ 66
3.4.2 Dimensionamento da bucha da articulação C ............................................. 69
3.5 DIMENSIONAMENTO DA ARTICULAÇÃO LATERAL A .................................... 70
3.5.1 Dimensionamento da bucha A ...................................................................... 71
3.5.2 Dimensionamento do eixo do mancal A....................................................... 71
3.5.3 Dimensionamento do mancal A .................................................................... 75
3.6 DIMENSIONAMENTO DO EIXO E e B ............................................................... 76
3.7 DIMENSIONAMENTO DO TUBO DO SUPORTE DO CILINDRO ...................... 80
3.8 DIMENSIONAMENTO DA BARRA AE ................................................................ 82
3.9 DIMENSIONAMENTO DA BARRA BD................................................................ 84
3.10 CÁLCULO DO SUPORTE DO CILINDRO ........................................................ 86
3.11 RESULTADOS OBTIDOS NOS CÁLCULOS ANALÍTICOS .............................. 87
4 SIMULAÇÃO NUMÉRICA PELO MÉTODO DOS ELEMENTOS FINITOS ........... 90
4.1 SIMULAÇÃO NUMÉRICA DE FLAMBAGEM DA HASTE DO CILINDRO........... 91
4.2 SIMULAÇÃO NUMÉRICA DO PANTÓGRAFO ................................................... 92
4.2.1 Tensões na barra AE ...................................................................................... 95
4.2.2 Tensões na barra BD...................................................................................... 96
4.2.3 Tensões no suporte do atuador .................................................................... 97
4.2.4 Tensões no tubo circular ............................................................................... 98
4.2.5 Tensões no mancal A..................................................................................... 99
4.2.6 Tensões no eixo B e E ................................................................................. 101
CONCLUSÃO ......................................................................................................... 104
15
REFERÊNCIAS ....................................................................................................... 106
ANEXO A - Propriedades do aço SAE 1045 cromado ........................................ 108
ANEXO B – Equações algébricas dos momentos de inércias de geometrias
comuns................................................................................................................... 109
ANEXO C – Propriedades das buchas Du do fabricante GGB .......................... 110
ANEXO D – Simulação de deformação do eixo no software AutoCAD
Mechanical ............................................................................................................. 111
ANEXO E – Propriedades do tubo ST 52 ............................................................. 112
ANEXO F – Dimensões dos tubos ST 52 ............................................................. 113
ANEXO G – Propriedades mecânicas dos aços nas condições laminados
normalizados e recozidos..................................................................................... 114
ANEXO H – Cálculo do momento fletor no software AutoCAD Mechanical..... 116
ANEXO I – Propriedades e dimensões dos tubos Dagan .................................. 117
ANEXO J – Propriedades de chapas de aço (Metalgusa) .................................. 118
13
INTRODUÇÃO
Atualmente, empresas nacionais fabricantes de máquinas estão perdendo
parcela de seu mercado para empresas internacionais (principalmente para
empresas do Oriente Médio), isso se deve a diferença de preço entre os produtos,
sendo o preço dos produtos das empresas internacionais mais baixo do que das
empresas nacionais.
O aumento na importação de máquinas e equipamentos gerou nos primeiros
quatro meses de 2011, um déficit comercial de US$ 5,5 bilhões, 33,3% a mais que o
déficit do mesmo período do ano passado, de US$ 4,1 bilhões. Estes números
mostram que as empresas nacionais estão perdendo cada vez mais o mercado,
necessitam tomar medidas urgentes para recuperar a parcela do mercado perdido,
para evitar na pior das hipóteses a falência das empresas mais prejudicadas. [5]
Para as empresas nacionais voltarem a serem competitivas, necessitam
aperfeiçoar seus produtos, o que exige projetos mais inovadores e bem
dimensionados, ou seja, projetos mais eficientes, dimensionados de acordo com as
necessidades do equipamento. Deve-se evitar projetos superdimensionados, que
aumentam o custo do equipamento, principalmente, através do desperdício de
matéria prima, entre elas o ferro que é um recurso finito.
Com base nesse problema, escolheu-se realizar o dimensionamento de um
mecanismo utilizado em várias máquinas, com o objetivo de realizar um projeto bem
dimensionado e seguro, minimizando ao máximo o gasto com matéria-prima e
evitando possíveis falhas da estrutura. O mecanismo escolhido foi um pantógrafo.
Seu pré-dimensionamento será realizado através de cálculos analíticos e
posteriormente comparado com simulações numéricas realizadas pelo método de
14
elementos finitos implementado pelo software Ansys, que gera cálculos mais
precisos para geometrias complexas, devido a simplificações realizadas para
resolver os cálculos analíticos.
A simulação numérica do método dos elementos finitos se trata de uma teoria
de cálculo que discritiza a peça a ser calculada em vários elementos e os calcula
individualmente através de equações diferenciais parciais. Para agilizar estes
cálculos são utilizados softwares de elementos finitos que importam a geometria de
software CAD, aplicam-se as condições de contorno, cargas e dados do material,
que servem de dados de entrada para o software resolver as equações diferenciais
parciais e gerar os resultados, que são apresentados de forma gráfica.
O dimensionamento do mecanismo pantográfico será realizado considerando
constantes suas principais características, como seu comprimento, largura, curso de
elevação, altura abaixada, posição do atuador hidráulico e massa a elevar.
Para alcançar o objetivo deste trabalho, faz-se inicialmente uma revisão de
resistências dos materiais e da teoria de elementos finitos. Na revisão de resistência
dos materiais é revisado carregamentos axiais, cisalhamento, torção, flexão, teoria
de falha de von Mises e flambagem. Na revisão de elementos finitos é apresentado
um exemplo simples de um cálculo, os principais passos e cuidados necessários ao
utilizar os softwares de elementos finitos. Após a revisão, realiza-se o
dimensionamento através de cálculos analíticos a partir da teoria de resistência dos
materiais, implementados com o auxilio de uma planilha no software Excel elaborada
para este trabalho e posteriormente cálculos numéricos através da teoria de
elementos finitos amparada pelo software Ansys, resultando em um projeto
dimensionado de acordo com as exigências de normas que regem equipamentos
que utilizam mecanismos pantográficos, tendo assim um equipamento seguro e sem
desperdício de matéria-prima.
Este trabalho propõem a metodologia de dimensionamento do pantógrafo,
que uma vez amparada em um software de elementos finitos poderia ser aplicada a
vários mecanismos pantográficos com tamanhos diferentes, com as mesmas
condições de contorno, agilizando o processo de dimensionamento do equipamento,
assim reduzindo o custo de desenvolvimento do mesmo e atendendo o cliente com
variedade de características técnicas e agilidade, reduzindo o prazo de entrega do
equipamento.
15
1 REVISÃO BIBLIOGRÁFICA
1.1 RESISTÊNCIA DOS MATERIAIS
1.1.1 Carregamento axial
Carregamento axial se caracteriza a uma peça simétrica de secção qualquer,
sendo submetida a uma força de tração ou compressão, sendo esta força aplicada
no centro da secção transversal em relação à direção da força. A Figura 1 mostra um
exemplo. [1]
Figura 1: Barra quadrada submetida ao carregamento axial [1]
O cálculo da tensão média (tensão normal representada pela letra grega
sigma σ) para carregamento axial, é representado pela Equação (Eq.) (1). Sendo A
igual à área da secção transversal da peça e F a força aplicada [1].
σ
med
=
F
A
(1)
Conforme expresso pela Eq. (1), as tensões normais são uniformemente
distribuídas em qualquer secção transversal ao eixo de uma barra. Porém, esta
suposição não se verifica nas vizinhanças do ponto de aplicação das forças, sendo a
16
determinação dessa tensão um problema estaticamente indeterminável, mas
resolvido pela teoria matemática da elasticidade. [1].
O princípio de Saint-Venant mostra que a tensão nas extremidades da
aplicação da carga P e da fixação possui um acréscimo de tensões provocadas pela
deformação específica superior nesta região, a Figura 2 apresenta a distorção da
malha, já longe da região de aplicação das tensões nota-se que a malha deforma-se
sem distorção (continuam paralelas), sendo nesta região válido o cálculo da tensão
pela Eq. (1). [1]
Figura 2: Princípio de Saint-Venant [2]
Sendo a tensão nos pontos de aplicação da carga sendo determinada por
métodos da matemática avançada ou experimentais, resultando em distribuições de
tensões conforme mostra o exemplo da Figura 3 para um perfil retangular. [1]
Figura 3: Distribuição de tensão para uma barra retangular com força concentrada [1]
17
Como foi visto anteriormente, o valor da tensão nas proximidades da
aplicação da carga concentrada é maior, o mesmo acontece quando a peça possui
descontinuidades como furos e variações bruscas de secção conforme exemplos
clássicos da Figura 4. [1]
Figura 4: Exemplos de geometrias que possuem concentradores de tensão [1]
Os valores dos concentradores de tensão para esses casos foram levantados
com estudos fotoelásticos e com esses foram desenvolvidas várias curvas, conforme
a Figura 5 e Figura 6, onde aplicam-se as relações geométricas das peças e obtémse um fator que multiplicado pela tensão média calculada pela Eq. (1), obtém a
tensão máxima conforme Eq. (2). [1]
Figura 5: Coeficientes de concentração de tensão para peças tracionadas com furo central [3]
18
Figura 6: Coeficientes de concentração de tensão para peças tracionadas por um eixo no centro do
furo [3]
σ
max
=
F
.k
A t
(2)
Sendo a área das geometrias da Figura 5 e Figura 6 calculada pela Eq. (3).
A = (w - d).t
(3)
1.1.2 Tensão de cisalhamento
A tensão de cisalhamento (representada pela letra grega tal
τ ) ocorre quando
a força é aplicada perpendicular ao comprimento da barra conforme representada na
Figura 7. O cisalhamento puro ocorre em situações que não há flexão junto à
mesma, que é o caso mostrado na Figura 7 e Figura 8, pelo fato da lâmina de corte
estar apertada contra os mordentes. [6]
Figura 7: Peça submetida à cisalhamento puro [6]
19
Figura 8: Cisalhamento na chapa do suporte (área Ac) [5]
A tensão de cisalhamento média é calculada pela Eq. (4), onde A é a área da
secção de transversal do comprimento da peça e F é a força aplicada. [6]
τ med = AF
(4)
Porém, se a peça estiver trabalhando com uma pequena folga, conforme
representada por x na Figura 9, essa será submetida à cisalhamento e momento
fletor, assim gerando um estado de tensão diferente ao mostrado na Figura 7. [6]
Figura 9: Peça submetida à cisalhamento e flexão [6]
Sendo assim, o cálculo do cisalhamento em peças submetidas à flexão e
cisalhamento é diferente do mostrado na Eq. (4) (cisalhamento puro), pois o
momento provoca cisalhamento na direção horizontal da peça. Esse fenômeno está
representado na Figura 10, onde podemos ver que há uma deformação nos
elementos superiores da viga em uma direção e nos elementos inferiores na direção
oposta, assim criando uma região de cisalhamento horizontal na viga que possui
maior magnitude no local da linha neutra.
20
Figura 10: Deformação de uma viga submetida à flexão [1]
Esta tensão de cisalhamento é calculada pela Eq. (5), obtida a partir da
integral τ
xy
F
=
I.t
y
∫ ydA . [6]
y1
τ xy = F.Q
I.t
(5)
Sendo F a força aplicada, I a inércia de área aplicada conforme a geometria
da peça, calculada pelas Eq. do anexo B, t a largura da peça conforme mostra a
Figura 11 e o momento estático representado por Q. [6]
Figura 11: Secção da barra submetida à cisalhamento [12]
O momento estático é calculado pela Eq (6). Onde A’ é a área da secção
transversal do ponto de onde se quer obter a tensão até a superfície externa da
peça e y é a distância entre o centróide da secção da peça ao centróide da área A’.
[6]
Q = A'.y
(6)
21
Assim resultando na distribuição de tensão de cisalhamento para perfis de
secção circular, quadrada e retangular conforme Figura 12. [1]
Figura 12: Distribuição da tensão de cisalhamento em perfis de secção circular, quadrada e
retangular [1]
Para os perfis “I” a distribuição da tensão de cisalhamento acontece diferente
dos perfis citados anteriormente, pelo fato da secção em questão possuir uma
variação brusca de largura na sua secção transversal, sendo a maior tensão na
menor largura da peça, conforme mostrado na Figura 13. [1]
Figura 13: Distribuição da tensão de cisalhamento no perfil ‘’I” [1]
O cálculo de cisalhamento realizado através da equação (5) aumenta
aproximadamente 20% a tensão para geometrias com secção quadrada ou circular
em relação ao cálculo realizado através da Eq. (4), porém superior para geometrias
com secção retangular com altura de 4 vezes a sua largura ou perfis como “I” ou
tubos que possuem mudanças bruscas da espessura t, sendo o ponto de maior
22
tensão de cisalhamento no centróide da secção transversal da peça e sua menor
tensão de cisalhamento na superfície da peça, onde o valor é 0. [1]
1.1.3 Tensão de esmagamento
Um pino engastado em suportes com furos como representado na Figura 14,
pode falhar de outros modos além do cisalhamento e do momento. As superfícies
cilíndricas laterais do pino e do furo em contato estão sujeitas à tensão de
esmagamento. Essas tensões tendem a esmagar o furo ou pino ao invés de cortá-lo,
essa tensão de esmagamento é normal representada pela letra grega sigma e pode
ser calculada pela Eq. (1), onde a área é a região de contato entre o furo e o pino,
sendo a área projetada, calculada pela Eq. (7), onde d é o diâmetro do eixo ou do
furo e t a largura da região de contato. [6]
Figura 14: Área de esmagamento [6]
A = d .t
(7)
1.1.4 Torção
A torção é um fenômeno físico que ocorre quando barras são solicitadas por
um movimento em relação ao seu eixo longitudinal, essa situação é comum em
eixos de transmissão em diversos outros elementos de máquinas em que o vetor do
momento aplicado seja paralelo ao eixo longitudinal de um corpo, em vez de ser
transversal a ele, que causaria flexão. Na prática, a maioria dos elementos de
máquinas possuem carregamentos combinados de torção e flexão conforme mostra
a Figura 15, pelo fato da força F se sobrepor no eixo. [6]
23
Figura 15: Exemplo de um eixo submetido à torção e flexão [7]
O torque provoca tensão de cisalhamento no eixo, esse que é representado
pela letra grega tau
τ
e calculado pela Eq. (8). Onde a letra T representa o torque
aplicado sobre a peça, c representa o local onde deseja-se obter a tensão, sendo
seu valor máximo obtido no raio externo da peça, conforme mostra a Figura 16 e J a
inércia polar. [1]
τ = T.c
J
(8)
A inércia polar é calculada através da integral expressa pela Eq. (9) que varia
conforme a geometria da peça; a integral pode ser transformada em Eq. algébrica,
representada pela Eq. (10) para secção transversal de tubos. [1]
(9)
c2 π c1 π
−
2
2
4
J=
4
(10)
24
Figura 16: Distribuição da tensão de cisalhamento devido ao torque [1]
A tensão obtida pela Eq. (8) não é válida para as regiões próximas a
aplicação do torque nem mesmo onde ocorrem variações bruscas de geometria,
pois nestas regiões existem concentradores de tensão, que em casos clássicos
podem ser obtidos por curvas semelhantes às mostradas Na seção 1.1.1, porém
para o torque. Como não terá aplicação para os casos clássicos no mecanismo
utilizado, não será feita a revisão desses itens. [1]
1.1.5 Flexão
Os fenômenos físicos denominados por flexão consistem em peças
submetidas a carregamentos transversais ao seu comprimento, esse tipo de peça
chama-se viga. Para facilitar o estudo da tensão encontrada nessas peças, supõe-se
que essas sejam submetidas somente a esforços de flexão, essa suposição é
chamada de flexão pura. A maioria das vigas reais também é submetida a
carregamentos de cisalhamento combinado com flexão. Nesses casos, devem-se
submeter às peças aos cálculos de uma teoria de falha, para se calcular uma tensão
normal equivalente ao carregamento combinado. Existem várias teorias, tanto para
materiais frágeis e dúcteis, algumas mais conservadoras, entre elas escolhe-se a
teoria da energia de distorção conhecida como a teoria de von Mises, pelo fato de
ser a mais precisa para materiais dúcteis,o que será visto na seção 1.1.6. [6]
A Figura 16 mostra uma viga submetida à flexão pela força F perpendicular ao
seu comprimento, essa força na sua posição atual causa o diagrama da força
cortante mostrado na Figura 18, que é utilizado para calcular a tensão de
cisalhamento e a Figura 19, o diagrama de momento fletor resultante das condições
de contorno da viga, usado para calcular a tensão normal de flexão pura nesta peça.
25
Figura 17: Imagem de uma viga submetida à flexão [12]
Figura 18: Diagrama de força cortante [12]
Figura 19: Diagrama de momento fletor [12]
26
A tensão normal ocasionada pela flexão pura pode ser calculada através da
Eq. (11), onde M é o momento fletor obtido no cálculo do diagrama de momento
fletor, c é a distância do centróide da secção transversal até a superfície mais
afastada do centróide e I a inércia de área, calculada para cada secção conforme
integral mostrada na Eq. (12), e representadas pelas equações algébricas do anexo
B. [1]
σ=
M.c
I
(11)
(12)
Figura 20: Variáveis para cálculo da inércia [1]
A tensão resultante do cálculo para Eq. (11) não é válido para regiões onde
ocorrem
variações
bruscas
da
geometria,
pois
nesses
pontos
ocorrem
concentradores de tensão, que podem ser obtidos para os casos clássicos através
da interpretação de um gráfico específico para o tipo de geometria e carregamento
das peças, com a entrada de parâmetros das características geométricas, para
obter-se o kt, que multiplicado pela tensão resulta na tensão máxima na peça. [1]
Logo a seguir observa-se o gráfico de concentração de tensão na Figura 21
para um eixo escalonado com raio de adoçamento, submetido ao carregamento de
flexão, usado para se obter o concentrador de tensão kt. [1]
27
Figura 21: Gráfico de Concentração de Tensão [3]
Então calcula-se a tensão máxima pela Eq. (13).
σ max =
M.c
.k t
I
(13)
1.1.6 Teoria de falha de von Mises
Como existem situações envolvendo tensões combinadas de normal e de
cisalhamento no mesmo ponto, necessita-se definir uma tensão equivalente que
possa ser usada para representar a combinação de tensões. A utilização da energia
de distorção (von Mises) nos dá um bom meio para fazê-lo para materiais dúcteis. A
tensão equivalente de von Mises é definida como a tensão de tração uniaxial que
criaria a mesma energia de distorção que é criada pela combinação atual das
tensões aplicadas. [6]
Para se obter a tensão de von Mises para um estado plano de tensões é
necessário primeiramente calcular as tensões máximas e mínimas obtidas pelos
diversos carregamentos que a peça foi submetida. A tensão máxima é mostrada
pela Eq.(14) e a tensão mínima é mostrada pela Eq. (15). [6]
σ max = σ 1 =
σx + σy
2
 σx - σy
+ 
 2
2

 + τ xy

2
(14)
28
σ min = σ 3 =
σx + σy
2
 σx - σy
− 
 2

2

 +τ 2
xy


(15)
Após calculada a tensão σ1 e σ3, aplicam-se os resultados obtidos na Eq.
(16), para calcularmos a tensão von Mises, sendo σ2 = 0 por se tratar de um estado
plano de tensão. [6]
σ
VM
= σ ² − σ .σ + σ ²
1
1
3
3
(16)
A equação (16) para um estado plano de tensões descreve uma elipse
mostrada na Figura 22, onde as tensões σ1 e σ3 devem estar no interior da mesma
para prevenir a falha sob escoamento para carregamentos estáticos. [6]
Figura 22: Elipse formada pela Eq. de von Mises para um estado plano de tensões [6]
Para obter a tensão de von Mises para um estado tridimensional usa-se a Eq.
(17), essa escreve um cilindro circular inclinado nos eixos σ1, σ2 e σ3, no qual cada
um dos 3 planos mostrados possui o ângulo de Euler de 45°, como mostra a Figura
23, sendo o seu interior uma região segura contra o escoamento com a combinação
de tensões. [6]
29
σ VM =
(σ x −σ y)² + (σ y −σ z)² + (σ z − σ x )² + 6(τ xy ² + τ yz ² + τ zx ²)
2
(17)
Figura 23: Elipses formadas pela Eq. de von Mises para o estado tridimensional [6]
O critério também é válido nos casos de peças submetidas à tensão de
cisalhamento puro, onde as tensões principais σ1=σ3=τ e σ2=0, resultando na tensão
de von Mises de mesmo valor que a tensão de cisalhamento, ocasionando a ruptura
na região da elipse representada pelos pontos A e B, conforme mostra
anteriormente a Figura 22. Para encontrar os valores admissíveis para os pontos A e
B aplica-se a Eq. (18). [6]
σ1 =
σe
3
(18)
Com base na Eq, (18), chega-se na Eq. (19), que define a tensão de
escoamento do material para cisalhamento.
τ e = σ e 0,577
(19)
1.1.7 Tensão admissível
A tensão admissível do material significa a capacidade do mesmo suportar
determinada tensão com segurança, devido a fenômenos não avaliados como a
fadiga dos materiais, essa é calculada pela Eq. (20) para os casos de tensão normal
e pela Eq. (21) pelos casos de tensão de cisalhamento. [6]
30
σ adm =
τ adm
=
σe
cs
(20)
τe
(21)
cs
Onde cs é o coeficiente de segurança que contempla, por exemplo, a perda
de resistência do material, a fadiga, garantindo uma vida mais longa para o
equipamento.
O
coeficiente
recomendado
pela
norma
EN
1570
(Safety
Requirements for Lifting Tables) que está sendo utilizada para dimensionar o
mecanismo é de 1,52.
1.1.8 Flambagem
Nas seções anteriores verificam-se teorias usadas para dimensionamento de
componentes estruturais, de modo que a carga não atinja valores superiores a sua
tensão de escoamento, nesta seção apontam-se critérios usados para dimensionar
estruturas prismáticas submetidas à compressão como por exemplo pilares para que
formem estruturas estáveis, ou seja, sua capacidade para suportar uma dada carga,
sem sofrer uma brusca mudança em sua configuração. Esse fenômeno é conhecido
como flambagem. [1]
Existem várias teorias que abordam este assunto, dessas foram escolhidas as
teorias mais indicadas para este trabalho, estas foram as de Euler, usadas para
vigas longas e a teoria empírica elaborada a partir de testes práticos para colunas
curtas e intermediárias, recomendadas pela American Institute Of Steel Construction
(AISC) para perfis de aço.
Para dimensionarmos uma peça prismática submetida à compressão,
inicialmente necessita-se calcular o comprimento efetivo da peça devido às
condições de contorno, conforme mostra a Figura 24. No qual L é o comprimento da
peça e Lo o comprimento efetivo. [1]
31
A: Uma extremidade
engastada e outra livre
C: Articulada
engastada
B: Biarticulada
D: Biengastada
Figura 24: Comprimento efetivo de flambagem (Lo) [1]
Posterior ao cálculo do comprimento efetivo, calcula-se o raio de giração da
peça, essa é calculada pela Eq. (22). Neste I é a menor inércia de área da secção
transversal da peça e A a área da mesma. [1]
r=
I
A
(22)
Feito isso, calcula-se a esbeltez da viga, essa é calculada pela Eq. (23), onde
Lo é o comprimento efetivo e r o raio de giração. [1]
λ=
Lo
r
(23)
Após achar a esbeltez, calcula-se o fator Cc pela equação (24), que
comparado com a esbeltez nos indica a metodologia de cálculo usada para obter a
tensão crítica. Sendo E, o módulo de elasticidade longitudinal do material conhecido
como módulo Yong e σe a tensão de escoamento do material. [1]
Cc =
2π ²E
σe
(24)
32
Para utilizar a metodologia de cálculo descrita por Euler, o valor da esbeltez
deve ser maior igual ao fator Cc e inferior e igual a 200, sendo assim utiliza-se a Eq.
(25) para calcular a tensão crítica de flambagem.
σ cr = π²E
Cc ≤ λ ≤ 200 :
λ²
(25)
Conhecendo a tensão crítica de flambagem determina-se a tensão admissível
para a viga através da Eq. (26), onde aplica-se o coeficiente de segurança 1,92
indicado pela AISC.
σ adm =
σ cr
1,92
(26)
Caso o critério da Eq. (25) não for atendido, deve-se usar a teoria para vigas
curtas e intermediárias, sendo o cálculo da tensão crítica expresso pela Eq. (27).
λ ≤ Cc ≤ 200 :
σcr = σ e .1−

λ² 
2 Cc² 
(27)
Para dimensionamento necessita-se saber a tensão admissível, que se
resume na divisão da tensão crítica pelo coeficiente de segurança, porém no caso
de vigas intermediárias e curtas o coeficiente de segurança não é constante como
no caso de Euler, necessita-se calcular a mesma. Essa é calculada pela Eq. (28).
CS =
5 3 λ  1 λ 
+ .
− .

5  8 Cc   8 Cc 
(28)
Após calcular o coeficiente de segurança, já se têm dados suficientes para
calcular a tensão admissível pela Eq. (29).
σ adm =
σ cr
CS
(29)
33
Sabendo a tensão admissível para a peça devido ao material e as condições
de contorno que a mesma vai ser submetida já se têm condições de dimensionar a
mesma para carregamento axial. Para isso calcula-se a tensão provocada pela
carga aplicada conforme a Eq. (1), na qual a tensão provocada pela carga não deve
ser superior à tensão admissível calculada pela Eq. (26) ou (29), que depende do
critério que a peça se enquadra devido a sua esbeltez.
1.2 TEORIA DE ELEMENTOS FINITOS
1.2.1 Introdução à teoria de elementos finitos e sua história
Diversos tipos de problemas físicos que são encontrados nas ciências e nas
engenharias são descritos matematicamente na forma de equações diferenciais
ordinárias e parciais. A solução exata usualmente é fruto de um método de solução
analítica encontrado através de métodos algébricos e diferenciais aplicados a
geometrias e condições de contorno particulares; a aplicação generalizada dos
métodos analíticos para diferentes geometrias e condições de contorno torna
impraticável ou até mesmo impossível a obtenção de soluções analíticas exatas. O
chamado Método dos Elementos Finitos (MEF) consiste em diferentes métodos
numéricos que aproximam a solução de problemas de valor de fronteira descritos
tanto por equações diferenciais ordinárias quanto por equações diferenciais parciais
através da subdivisão da geometria do problema em elementos menores, chamados
elementos finitos, nos quais a aproximação da solução exata pode ser obtida por
interpolação de uma solução aproximada. [8]
O MEF foi originalmente concebido pelo matemático Courant à época da II
Guerra Mundial através da publicação de um artigo em 1943. Como nessa época
ainda não haviam sido desenvolvidos computadores capazes de realizar uma
grande quantidade de cálculos matemáticos, o método matemático foi ignorado pela
academia durante vários anos. [8]
Na
década
de
1950,
engenheiros
e
pesquisadores
envolvidos
no
desenvolvimento de aviões a jato na Boeing iniciaram os primeiros trabalhos práticos
no estabelecimento do MEF aplicados à indústria aeronáutica. M. J. Turner, R. W.
Clough, H. C. Martin e L. J. Top ppublicaram em 1956, um dos primeiros artigos que
34
delinearam as principais ideias do MEF, entre elas a formulação matemática dos
elementos e a montagem da matriz de elementos. Mas, no artigo ainda não se fazia
referência ao nome “elementos finitos” para designar os elementos de discretização
da geometria do problema físico. O segundo co-autor do artigo, Ray Clough era na
época, professor em Berkeley que descreveu o método com o nome de “método dos
elementos finitos” num artigo publicado subsequentemente. Os seus trabalhos
deram início a intensas pesquisas em Berkeley por outros professores, entre eles E.
Wilson e R. L. Taylor, juntamente com os estudantes de pós-graduação T. J. R.
Hughes, C. Felippa e K. J. Bathe. Durante muitos anos, Berkeley foi o principal
centro de pesquisa em MEF. Essas pesquisas coincidiram com a rápida
disseminação de computadores eletrônicos nas universidades e institutos de
pesquisas, que levaram o método a se tornar amplamente utilizado em áreas
estratégicas à segurança americana durante o período da Guerra Fria, tais como
pesquisa nuclear, defesa, indústria automotiva e aeroespacial. [8]
1.2.2 Conceito do método de elementos finitos
O método dos elementos finitos surgiu como uma nova possibilidade para
resolver problemas da teoria da elasticidade, superando as dificuldades e problemas
inerentes aos métodos de Rayleigh-Ritz, Galerkin, diferenças finitas, ponderados e
outros. [7]
Nos dois primeiros métodos, nem sempre é fácil de obter funções
aproximadas que satisfaçam as condições de contorno irregular e saber se elas se
aproximam da função exata. [7]
Além disso, para melhorar a precisão dos resultados é preciso considerar
sempre funções de ordem superior às anteriormente propostas, o que torna o
cálculo muito trabalhoso e em certos casos, até infactível. [7]
O método de elementos finitos comumente utilizado é baseado no método de
Rayleigh-Ritz e prevê a divisão do domínio de integração, contínuo, em um número
finito de pequenas regiões denominadas elementos finitos, tornando o meio contínuo
em discreto, como mostrado no elemento hachurado da Figura 25. [7]
35
Figura 25: Rede de elementos finitos [7]
A essa divisão dá-se o nome de rede de elementos finitos. A malha desse
reticulado pode ser aumentada ou diminuída variando o tamanho dos elementos
finitos. Os pontos de intersecção das linhas dessa rede são chamados de nós. [7]
1.2.2.1.Exemplo de um cálculo simples através do método de elementos finitos
Irá se tentar expor abaixo, a ideia básica do método dos elementos finitos
através do seguinte exemplo:
Considerando o problema de determinação da área de um círculo de raio R
representado por um conjunto de triângulos conforme mostra a Figura 26, a área
aproximada do círculo será a soma das áreas dos triângulos usados na
representação do círculo. Embora esse exemplo possa parecer trivial, todavia ele
ilustra várias ideias e passos envolvidos no método dos elementos finitos. [9]
A resolução do problema será representada nos passos 1 e 2:
1 - Discretização do elemento finito: Primeiro, a região contínua (o círculo) é
representado por um conjunto de n elementos, que nesse caso são triângulos. Cada
subregião é chamada de elemento. O conjunto de elementos é chamado de malha
de elementos finitos. Nesse caso, discretiza-se o círculo em uma malha de cinco
triângulos (n=5). Desde que todos os elementos tenham o mesmo tamanho, a malha
é considerada uniforme. [9]
36
Figura 26: Círculo com cinco elementos do tipo triângulo [9]
Figura 27: Dimensões do elemento [9]
2 - Equação dos elementos: Agora define-se a equação que nos possibilita o cálculo
da propriedade desejada do elemento, no caso a área mostrada na Figura 26. O
cálculo é realizado inicialmente com as relações geométricas do elemento, onde n é
o número de elementos que compõem o círculo. [9]
θ = 2π/n
(30)
b = R.senθ/2
(31)
h = R.cosθ/2
(32)
1 
ae = 2. b.h 
2 
(33)
37
A incógnita ae é a área de um elemento triangular que compõe o círculo. Temse então para o elemento ae.
ae =
R²
 2π 
sen. 
2
 n 
(34)
Onde R é o raio do círculo. Então, a área aproximada do círculo é a soma dos
n elementos. Dentro desse contexto, é válido dizer que conforme vai-se aumentando
o número de elementos da malha, obtêm-se cada vez resultados mais próximos ao
real. Assim sendo, quando tendermos n ao infinito iremos aproximar em muito o
resultado ao resultado obtido pela fórmula padrão para o cálculo de área de círculos
(A= π R²). [9]
Ao invés de buscar uma função admissível que satisfaça as condições de
contorno para todo o domínio, no método dos elementos finitos, as funções
admissíveis são definidas no domínio de cada elemento finito. [7]
Para cada elemento i, é montado um funcional Пi que, somado aos dos
demais elementos finitos, formam o funcional П para todo o domínio, mostrado na
Eq. (35). [7]
(35)
Para cada elemento i, a função aproximada é formada por variáveis referidas
aos nós do elemento (parâmetros nodais) e por funções denominadas de funções de
forma. Assim, a função aproximação v tem a forma mostrada na Eq. (36), onde aj
são os parâmetros nodais e Φj as funções de forma. [7]
(36)
O funcional П fica expresso pela Eq. (37).
38
(37)
A condição de estacionaridade gera, como no método de Rayleigh-Ritz, um
sistema de equações algébricas lineares, conforme a mostrada pela Eq. (38). [7]
(38)
A solução do sistema de Eq. (38) dá os valores dos parâmetros nodais aj que
podem ser deslocamentos, forças internas, ou ambos, dependendo da formulação
do método dos elementos finitos que se utiliza. [7]
Se o campo deslocamento é descrito por funções aproximadas e o princípio
da mínima energia potencial é empregado, as incógnitas são as componentes dos
deslocamentos nodais e o método dos elementos finitos é denominado modelo dos
deslocamentos ou método dos elementos finitos, método da rigidez. [7]
Se o campo de tensões ou esforços internos é representado por funções
aproximadas, as incógnitas são tensões ou esforços internos nodais e o método dos
elementos finitos é denominado modelo das forças ou método dos elementos finitos,
modelo da flexibilidade, sendo utilizado o princípio da mínima energia complementar.
[7]
Nos métodos mistos, as funções aproximadas são expressas em termos de
deslocamentos e forças internas ou tensões são derivados de variacionais
generalizadas, como o princípio de Reissner.[7]
1.2.3 Fundamento do método de elementos finitos
Conforme a viga prismática da Figura 28, da qual se quer determinar a flecha
e a rotação da extremidade livre, são conhecidos a carga uniforme q, o comprimento
l da viga, o módulo Young E e o momento de inércia I da secção da viga. [7]
Para resolver este problema com o método de Rayleigh-Ritz, adota-se, por
exemplo, para representar as deflexões do eixo baricêntrico da viga, a função
aproximada da Eq. (39). [7]
39
v(x) = a 1 + a 2 x + a 3 x 2 + a 4 x 3
(39)
Figura 28: Viga prismática em balanço [7]
As condições de contorno para esse caso são: se v(0)=0 então a1=0 e se
v´(0)=0 então a2=0
Logo, aplicando-se as condições de contorno na Eq. (39), resulta na Eq. (40).
[7]
v(x) = a 3 x 2 + a 4 x 3
(40)
Sabendo que v(l)=-fev’(l)=-θ,onde F é a deflexão e θ a rotação na
extremidade livre da viga, tem-se o sistema de Eq. mostradas na Eq. (41) e (42).[7]
a 3l2 + a 4 l3 = −f
(41)
2.a 3 l + 3.a 4 l 2 = −θ
(42)
Resolvidas, fornecem as Eq. (43) e (44).
a3 =
θ 3f
−
l l2
(43)
40
a4 =
2f
l3
−
θ
l2
(44)
Então v(x) passa a ser escrita conforme mostrado na Eq. (45).
 2x 3 3x 2
v (x) = 
−
 3
l
l2

3 

 2
.f +  x − x .θ .l

 2

l3 
l

(45)
Introduzindo a coordenada adimensional ξ = x/l, a igualdade acima fica
expressa pela Eq. (46).
v (ξ ) =  2ξ 3 − 3ξ 2 .f +  ξ 2 − ξ 3 .θ .l




(46)
Nota-se que a função aproximada agora é diretamente dependente das
incógnitas do problema, ou seja, de f e θ.
A energia potencial total para o caso é dada pela Eq. (47).
(47)
Derivando duas vezes a igualdade (46) e introduzindo-a em (47), obtém-se a
Eq. (48). [7]
(48)
A condição de estacionaridade do funcional anterior exige as condições
mostradas pelas Eq. (49) e (50), essas são obtidas após integrarmos a Eq. (48),
para o intervalo de 0 a 1, e derivamos ela parcialmente em relação a f e θ. [7]
41
(49)
(50)
A solução desse sistema de Eq. nos fornece a Eq. (51).
(51)
Vê-se então, que a função aproximada pode ser expressa em função das
incógnitas do problema, ao invés do parâmetro de deslocamentos ai. [7]
Admitindo que a deflexão e a rotação na extremidade sejam representadas
por v1 e θ1, respectivamente, e na extremidade livre por v2 e θ2, respectivamente,
como mostra a Figura 29, a função aproximada pode ser escrita como mostra a Eq.
(52). [7]
(52)
Sendo:
e
Nota-se que a igualdade da Eq. (52) é a expansão do somatório da igualdade
da Eq. (36), sendo Φ1 as funções de forma e v1 e θ1 os parâmetros nodais. [7]
As outras duas funções: Φ1(ξ) e Φ2(ξ) são indeterminadas, já que v1=0 e θ1=0
para o problema em análise. [7]
42
Figura 29: Deslocamentos e esforços nodais positivos [9]
Mas admitindo valores não nulos para v1 e θ1 e deixando para impor as
condições de contorno mais adiante, as funções Φ1(ξ) e Φ2(ξ) podem ser
determinadas. Basta voltar à igualdade da Eq. (39) e fazer:
se v(0) = v então : a = v
1
1
1
se v' (0) = θ então : a = θ
1
2
1
se v(l) = v então : v = v + θ .l + a .l2 + a .l3
2
2
1
1
3
4
se v' (l) = θ então : θ = θ + 2a .l + 3a .l2
2
2
1
3
4
Os valores de a3 e a4 são obtidos resolvendo esse sistema de quatro Eq. e
quatro incógnitas:
a =
(
3. v − v
3
2
l
2
1
)- θ
2
+ 2θ
1
l
θ
2
e
a =
(
2. v − v
4
1
l
3
2
)- θ + θ
1
l
2
2
Resulta, então, a função aproximada da Eq. (53)
(53)
Assim, tem-se:
43
Matricialmente pode-se exprimir a igualdade da Eq. (52), como na Eq. (54).
Onde Φ é a matriz das funções de forma e V o vetor das componentes dos
deslocamentos nodais ou incógnitas nodais. [7]
(54)
Observar que as funções de forma têm valor unitário nos pontos onde se
determinam as incógnitas e nulo nos demais. Por exemplo: no ponto 1 tem-se:
E no ponto 2:
Derivando duas vezes a igualdade da Eq. (53), obtém-se a Eq. (55).
(55)
Ou em forma matricial, mostrado na Eq. (56):
v' ' (ξ ) = Bv
(56)
Substituindo a Eq. (55) no funcional que representa a energia potencial total,
tem-se:
44
Efetuando o quadrado e integrando obtém-se:
A minimização desse funcional é realizada derivando-o em relação às
incógnitas v1, θ1, v2 e θ2, já denominadas incógnitas nodais, uma vez que se passa a
chamar de nós os pontos 1 e 2 da viga. [7]
Dessa maneira, obtém-se o seguinte sistema de equações mostrado nas Eq.
(57). [7]
(57)
Simplificando e escrevendo matricialmente, obtém-se a matriz da Eq. (58).
(58)
Onde temos a forma mostrada na Eq. (59).
k.v = r
(59)
45
Impondo, agora, as condições de contorno: v1 = θ1 = 0, o sistema de Eq. (58)
se reduz à matriz mostrada na Eq. (60), cuja a solução conduz aos valores já
determinados para f e θ respectivamente. [7]
(60)
Uma outra maneira de resolver o sistema de Eq. (58) consiste em anular as
linhas e colunas relativas a v1 e θ1 (1ª e 2ª) da matriz quadrada e substituir os dois
primeiros termos da diagonal por 1 e anular os dois primeiros termos do vetor do
lado direito da igualdade, resultando na matriz da Eq. (61), cuja a solução leva aos
valores de v2 e θ2. [7]
Deve-se notar que a matriz quadrada da Eq. (58) é simétrica e estas
propriedades independem do problema analisado. [7]
(61)
Basta analisar as igualdades da Eq. (57) e verificar, por exemplo, que
a) Na primeira igualdade, o coeficiente θ1, obtido com ∂ ∏ ∂v , é igual ao
1
coeficiente de v1 obtido de ∂ ∏ ∂θ da segunda igualdade; [7]
1
b) Na terceira igualdade, o coeficiente v1, obtido com ∂ ∏ ∂v , é igual ao
2
coeficiente de v2 da primeira igualdade, obtido de ∂ ∏ ∂v ; [7]
1
46
Figura 30: Viga dividida em duas partes, possuindo dois elementos e três nós [9]
Generalizando o caso da Figura 28, para quando tivermos 3 ou mais nós
conforme Figura 30, temos a matriz abaixo: [7]
Se a viga da Figura 28 for dividida em n elementos (de tamanhos diferentes),
o sistema de Eq. que resulta, procedendo de maneira análoga ao que foi feito com a
viga para dois elementos e é esquematizado na Figura 31. [7]
47
Figura 31: Configuração da matriz de uma viga com mais de um elemento [9]
1.2.4 Etapas de uma análise numérica através de um software de MEF
De forma genérica, a modelagem através do MEF possui etapas operacionais
bem definida, conforme descrito abaixo: [10]
1. Descrição geométrica da região do espaço considerado (modelo do CAD).
2. Geração de uma malha de elementos interconectados por nós.
3. Definição de equações diferenciais parciais (EDPs) e respectivas condições
de contorno (ou iniciais, ou ambas) que regem o problema.
4. Solução numérica do sistema algébrico resultante.
5. Pós-processamento de resultados para visualização, conforme, Figura 32.
48
Figura 32: Pós-processamento de resultados para visualização [11]
Essas etapas de operação podem ser executadas por diferentes programas
de modo independente. Por exemplo, um modelo de um componente mecânico feito
numa ferramenta de CAD – Computer Aided Design – pode ser fornecido a um
programa de geração de malhas, que por sua vez pode gerar a entrada para um
programa que contenha um núcleo de solução numérica (solver) e finalmente, o
resultado
obtido
pelo
solver
pode
ser
visualizado
numa
ferramenta
de
processamento gráfico. [10]
Recentemente, embora o desenvolvimento tecnológico tenha trazido avanços
notáveis para o MEF – sobretudo na capacidade de cálculo dos desktops, cujo
desempenho atual é compatível ao que só estações de trabalho poderiam alcançar
até poucos tempos anos atrás – essa técnica não é uma resposta mágica para todos
os tipos de problemas descritos por EDPs. Problemas como hiper-rigidez numérica,
erros de aproximação, má qualidade da malha e má escolha de condições iniciais e
de contorno por parte do usuário podem resultar em péssimas interpretações de
análises pelo uso incipiente do MEF. Ainda assim, mesmo que adequadamente
submetido a validações em problemas reais, o MEF tem se demonstrado uma
ferramenta de engenharia excepcionalmente poderosa. Dessa forma, observa-se
que o conhecimento das bases teóricas do método é um fator determinante para o
bom ou mau uso de tal ferramenta [10].
49
2 MECANISMO PANTOGRÁFICO
O mecanismo pantográfico é usado em máquinas para elevar cargas ou até
mesmo empurrar cargas, esse tem a característica de possuir um elevado curso sem
a necessidade de estruturas para guiar o seu movimento.
2.1 PRINCIPAIS COMPONENTES DO MECANISMO PANTOGRÁFICO
O mecanismo pantográfico é formado pelas peças descritas na Tabela 1 e
representadas na Figura 33.
Tabela 1: Peças que compõem o mecanismo pantográfico [12]
Item
01
02
03
05
06
07
08
09
11
Descrição
Conjunto alavanca 1
Conjunto alavanca 2
Conjunto eixo central
Bucha maior
Rolo
Conjunto eixo do atuador
Bucha menor
Atuador hidráulico
Conjunto eixo lateral
Figura 33: Desenho em perspectiva do mecanismo pantográfico [12]
50
2.1.1 Componentes que formam o conjunto de alavancas 01
Os componentes que formam o conjunto alavanca 01 da Figura 34 são
mostrados na Tabela 2.
Item
01
02
03
04
05
06
Tabela 2: Peças que compõem o conjunto alavanca 1 [12]
Descrição
Alavanca
Mancal lateral
Eixo
Mancal central
Tampa
Tampa
Figura 34: Desenho em perspectiva da alavanca 01 [12]
2.1.2 Componentes que formam o conjunto de alavancas 02
Os componentes que formam o conjunto alavanca 02 da Figura 35 são
mostrados na Tabela 3.
Tabela 3: Peças que compõem o conjunto alavanca 2 [12]
51
Item
01
02
03
04
05
06
07
08
09
Descrição
Alavanca
Mancal Lateral
Eixo
Mancal Central
Tampa
Tampa
Tubo suporte do atuador
Suporte
Reforço
Figura 35: Desenho em perspectiva da alavanca 02 [12]
2.2 APLICAÇÕES DO MECANISMO PANTOGRÁFICO
O mecanismo pantográfico possui várias aplicações em máquinas, entre
essas aplicações as que se destacaram foram às empregadas em máquinas para
manipulação de cargas, como mesas elevatórias e Push/Pulls.
A mesa elevatória mostrada na Figura 36 é utilizada para movimentar cargas
na vertical, sendo empregadas em tarefas de elevação de cargas entre pavimentos
de fábricas, no carregamento de cargas em veículos e em linhas de produção, onde
essa é usada para manter a carga sempre a uma altura ergonômica para o
operador.
52
Figura 36: Mesa elevatória [13]
O Push/Pulls mostrado na Figura 37, é acoplado a uma empilhadeira e
utilizado como acessório para a mesma, agilizando o processo de manipulação de
cargas, o pantógrafo utilizado no Push/Pulls possui movimentos horizontais, com a
função de puxar a carga sobre os fardos e empurrar a mesma, agilizando o
transporte e eliminando a utilização de pallet.
Figura 37: Push/Pulls [14]
2.3 CARACTERÍSTICAS TÉCNICAS
O dimensionamento do mecanismo pantográfico será realizado considerando
que ele se movimentará na vertical e seja submetido a forças na mesma direção,
conforme a Figura 38.
53
Figura 38: Movimento do mecanismo pantográfico [12]
As características técnicas desejadas para o mecanismo estão na Tabela 4.
Estas serão utilizadas para realizar o dimensionamento da estrutura que compõe o
pantógrafo.
Tabela 4: Características técnicas [12]
Descrição
Massa a elevar (m)
Curso de elevação
Comprimento da Alavanca (L1)
Largura máxima do pantógrafo
Acionamento por atuadores hidráulicos
Ângulo θ1
Ângulo θ2
L2
L3
L4
Valor
2500 kg
1500 mm
2210 mm
1465 mm
2 peças
5,82 °
19,00 °
1105 mm
252 mm
112 mm
54
3
DIMENSIONAMENTO
DO
MECANISMO
ATRAVÉS
DE
CÁLCULOS
ANALÍTICOS
Com base nas características técnicas exigidas, inicia-se o dimensionamento
dinâmico do equipamento através dos cálculos da estática e de cálculos analíticos
realizados através da teoria de resistência dos materiais com o intuito de modelar
este no Software Solid Works para posteriormente realizar os cálculos de elementos
finitos do mesmo implementado através software Ansys. O dimensionamento
analítico segue a seqüência mostrada no fluxograma da Figura 39.
Figura 39: Fluxograma do dimensionamento analítico do mecanismo [12]
55
3.1 DETERMINAÇÃO DA FORÇA DINÂMICA DE ELEVAÇÃO
O mecanismo pantográfico adotado possui capacidade de elevar a massa de
2500 kg. Para saber a força necessária para elevar essa carga, deve-se realizar os
cálculos dinâmicos do mecanismo, como não se têm todas as dimensões e massas
do mecanismo definidas, não conseguimos calcular a inércia de massa do mesmo
para realizar os cálculos dinâmicos. Então se buscou na norma EN 1570-1998
(Safety Requirements for Lifting Tables) um fator que multiplicado pela massa a ser
elevada, que resulta em uma força máxima que este tipo de mecanismo é submetido
devido aos esforços dinâmicos, sob as condições de trabalhos e velocidades de
operações citadas na norma.
Como quer se dimensionar o mecanismo para carregamentos verticais buscase o coeficiente para o mesmo, este é de 1,4, então a força dinâmica máxima que o
mecanismo será submetido para elevar a massa de 2.500 kg será calculada pela Eq.
(62), resultando na força dinâmica máxima expressa pela Eq. (63). [1]
F = m.1,4.g
F = 2500 kg.1,4.10 m/s² = 35000 N
(62)
(63)
Onde, g é a aceleração da gravidade, sendo adotado o valor de 10 m/s², e m
a massa a ser elevada em kg.
3.2 CÁLCULO DAS REAÇÕES DO MECANISMO
Para cada posição de elevação, o mecanismo possui uma nova condição de
cálculo, devido a isso se deve encontrar a pior situação para realizar os cálculos.
Após alguns cálculos preliminares, chega-se a conclusão que a pior situação ocorre
quando o mecanismo está abaixado, pois o comprimento das suas alavancas fica
maior na horizontal, e a força do cilindro é superior devido ao pequeno ângulo entre
a linha de centro do cilindro e o plano horizontal. Então se define realizar o
dimensionamento estático na posição abaixada do mecanismo.
56
A Figura 40 mostra o mecanismo pantográfico abaixado, onde aplica-se a
carga no centro de DE, representado por F1, resultando na distribuição de forças na
posição abaixada FD, y = FE, y = 1/2 F1 .
Figura 40: Desenho do mecanismo abaixado com carga no centro de DE [12]
Inicialmente realiza-se o somatório das F na direção y (vertical), conforme
mostrado na Eq. (65).
∑ Fy = 0
- FD, y - FE, y + FA, y + FB, y + FCil .sen θ 2 -F C, y = 0
(64)
(65)
Como as forças FD,y+FE,y=FB,y+FA,y se anulam, obtém-se a Eq. (66).
0 + FCil .sen θ 2 - FCy = 0
(66)
Isolando a força FC,y da Eq. (66), obtemos a Eq. (67).
FC, y = FCil .sen θ 2
(67)
57
Posteriormente realiza-se o somatório das F na direção x (horizontal),
conforme mostra a Eq. (69).
∑ Fx = 0
(68)
FD, x - FE, x + FA, x -F B, x +(FCil .cos θ 2 ) -F C, x = 0
(69)
Como as forças FA,x+FD,x = FB,x+FE,x, se anulam, obtém-se a Eq. (70).
FC, x = FCil .cos θ 2
(70)
Isola-se a barra BD, conforme mostrado na Figura 41 e realiza-se o somatório
dos momentos e C na Eq. (72).
Figura 41: Barra BD [12]
∑ MC = 0 (Positivo no sentido anti-horário)
(F D, y .L 2 .cos θ 1 ) + (F B, y .L 2 .cos θ 1) - (FC .L 3 ) = 0
(71)
(72)
Isolando a força do cilindro da Eq. (72), obtém-se a Eq. (73), no qual se
alimentam os dados e obtém-se a força de reação no cilindro mostrado na Eq. (74).
58
FCil =
FCil =
(F D, y .L 2 .cos θ1 ) + (FB, y .L 2 .cos θ1 )
L3
(17500 N.1105 mm.cos 5,82°) + (17500 N.1105 mm.cos 5,82°)
= 152681N
252
(73)
(74)
Posterior ao cálculo da força do cilindro, calcula-se as forças nos eixos
centrais C e no eixo lateral A. Para calcular a força no eixo C calculou-se
inicialmente a forças nas componentes x e y, através das Eq. (67) e (70), onde
obtêm-se as forças mostradas nas Eq. (75) e (76).
FC, y = 152681 N.sen 19° = 49708 N
(75)
FC, x = 152681 N.cos 19 ° = 144363 N
(76)
Sabendo as forças em x e y consegue-se obter a resultante no eixo C através
da Eq. (77).
FC = FC,x ² + FC,y ² = 152681 N
(77)
Observa-se que a força no eixo central, eixo C, é a mesma força do cilindro
para esta posição.
Para realizar os cálculos das forças do eixo lateral A, calcula-se as reações
em x e y, para isso deve-se fazer o somatório das forças da barra AE, mostradas na
Figura 42 através da Eq. (64).
Figura 42: Barra AE [12]
59
Obtendo a Eq. (78):
R A, y = FE, y - FC, y = -32208 N
(78)
Para calcular a RA,x realiza-se o somatório das forças na direção x,
representado pela Eq. (68), resultando na Eq. (79).
R
A, x
= −F
C, x
= −144363N
(79)
Com esses dados consegue-se obter a força resultante que estará agindo no
eixo, aplicando a Eq. (80).
F = R
A
A, x
²+R
A, y
² = 147912 N
(80)
Para melhor visualização dos resultados, vamos representar os mesmos na
Tabela 5.
Tabela 5: Resultados das reações nos eixos e cilindro [12]
Descrição
Força [N]
Força no Cilindro (FCil)
152681
Eixo A
147912
Eixo B
17500
Eixo C
152681
Eixo D
17500
Eixo E
17500
Com o intuito de validar os resultados obtidos nos cálculos analíticos, modelase o mecanismo de maneira simplificada no software de CAD SolidWorks, conforme
mostrado na Figura 43 e com auxílios do software Motion realiza-se uma simulação
de movimento do mecanismo, o qual neste módulo calcula-se as reações do
mecanismo para cada posição de elevação, este não é um cálculo dinâmico pelo
fato de não se ter atribuído às acelerações do mecanismo.
Os parâmetros que são fornecidos ao software são as forças FD,y e FE,y
representadas pelas setas azuis, a aceleração da gravidade representada pela seta
60
verde de 10 m/s² e o atuar representado pela seta vermelha, no qual define-se a
velocidade de trabalho de 40 mm/s e a direção do mesmo.
Figura 43: Modelo do mecanismo avaliado no Motion [12]
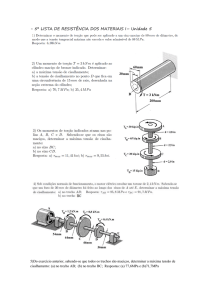
Com a simulação, obtêm-se as forças em relação a tempo de elevação,
sendo o tempo de 14 s equivalente a elevação máxima, como pode-se ver na Figura
44: Gráfico da força do atuador em relação ao tempo, Figura 45: Gráfico da força do
eixo A em relação ao tempo, Figura 46: Gráfico da força do eixo B em relação ao
Força do motor1 (newton)
tempo e Figura 47: Gráfico da força do eixo C em relação ao tempo.
152632
134345
116057
97769
79481
0.00
1.40
2.80
4.20
5.60
7.00
Tempo (sec)
8.40
9.80
11.20
12.60
14.00
12.60
14.00
Força de reação23 (newton)
Figura 44: Gráfico da força do atuador em relação ao tempo [12]
147863
126977
106091
85205
64319
0.00
1.40
2.80
4.20
5.60
7.00
Tempo (sec)
8.40
9.80
11.20
Figura 45: Gráfico da força do eixo A em relação ao tempo [12]
Força de reação20 (newton)
61
17504.921
17504.915
17504.909
17504.903
17504.897
0.00
1.40
2.80
4.20
5.60
7.00
Tempo (sec)
8.40
9.80
11.20
12.60
14.00
Força de reação18 (newton)
Figura 46: Gráfico da força do eixo B em relação ao tempo [12]
152631
134342
116054
97765
79476
0.00
1.40
2.80
4.20
5.60
7.00
Tempo (sec)
8.40
9.80
11.20
12.60
14.00
Figura 47: Gráfico da força do eixo C em relação ao tempo [12]
3.3 DIMENSIONAMENTO DO ATUADOR
O acionamento vai ser realizado por atuadores hidráulicos que transformam o
trabalho hidráulico em um trabalho mecânico. Esse vai ser realizado com duas
peças, pois ao colocar dois atuadores, um em cada extremidade do tubo, conforme
mostrado anteriormente na Figura 33, minimiza a flexão no mesmo que será o
suporte do atuador hidráulico.
O dimensionamento do atuador abordado resume-se no cálculo do diâmetro
da camisa para obter-se a força necessária no mecanismo e o diâmetro da haste
para evitar que a mesma flambe, para especificar o atuador para compra.
3.3.1 Dimensionamento do diâmetro da camisa
O diâmetro da camisa será dimensionado considerando que o circuito
hidráulico disponha uma pressão (p) de 20 N/mm² (200 bar) na entrada da conexão
do cilindro. Este será realizado através da Eq. (81), aonde F= Fcil/2.
62
p=
F
A
=
d=
F
= 69,7mm
p.π
4
(81)
Obtendo um diâmetro de 69,7 mm através do cálculo expresso pela Eq. (81),
então adota-se o diâmetro comercial mais próximo, sendo de maior diâmetro que o
mínimo calculado, assim este tubo terá 76,2 mm (3”) de diâmetro interno, assim
reduzindo a pressão devido ao aumento da área, essa mudando para 16,7 N/mm²
(167 bar).
3.3.2 Dimensionamento da haste do atuador
Para realizar o dimensionamento da haste, é necessário que saibamos a
força do atuador e o comprimento do mesmo, e o tipo de fixação desse. Como podese observar anteriormente nos gráficos da Figura 44, a força do cilindro está
diminuindo conforme o pantógrafo se eleva e o comprimento do cilindro está
aumentando, então não se tem condições de afirmar que o caso crítico acontece
quando o cilindro está aberto. Para verificarmos o caso crítico,faz-se vários cálculos
da força do atuador hidráulico variando o curso do pantógrafo em intervalos de 100
mm até chegar ao seu curso máximo. Os cálculos são realizados para cada posição
conforme mostrado na seção 3.2, agregando o cálculo do comprimento do atuador.
Realizou-se estes com o auxílio de uma planilha elaborada no software Excel.
Os resultados obtidos do comprimento do atuador em relação à elevação do
pantógrafo estão representados no gráfico da Figura 48 e a força de cada atuador
em relação ao comprimento do mesmo estão representados no gráfico da Figura 49.
63
Figura 48: Elevação do pantógrafo x Comprimento do atuador [12]
Figura 49: Força de 1 atuador x comprimento do atuador [12]
Para realizar os cálculos de flambagem do atuador temos que simplificar a
geometria do mesmo, a simplificação se resume em considerar que o atuador tem
seu diâmetro constante de mesmo valor que a haste, pois se trata do menor
diâmetro, sendo este o mais vulnerável à flambagem.
Como agora se sabe a força do atuador e do comprimento do mesmo para
cada uma das situações que o mesmo será submetido. Temos, então, condições de
verificar se a haste suportará a carga, a mesma possui as propriedades mostradas
64
na Tabela 6. Inicialmente, realiza-se o cálculo da inércia da secção transversal pela
Eq. (82) e área da secção transversal pela Eq. (83) para se calcular o raio de giração
da haste. Esse cálculo é realizado pela Eq. (22), obtendo o valor mostrado na Eq.
(84).
Tabela 6: Propriedades da haste [12]
Diâmetro da haste (d)
σe(Tensão de escoamento do material)
E (Módulo de Elasticidade Longitudinal)
Condição de contorno da fixação (Figura 24)
35 mm
350 MPa
200.000 MPa
1 (bi-articulados)
35 ².π
= 962 mm ²
4
(82)
I=
35 4.π
= 73662 mm 4
64
(83)
r=
73662
= 8,75mm
962
(84)
A=
Sabendo o raio de giração, calcula-se a esbeltez pela Eq. (23), para cada
comprimento do atuador, obtendo os valores representados pelo gráfico da Figura
50.
Figura 50: Esbeltez da haste [12]
65
Após, calcula-se o Fator Cc pela Eq. (24), para verificar o critério de cálculo
usado para cada uma das 16 condições, obtém-se o fator Cc = 106. Com base
nesse, sabemos que temos que realizar o cálculo da tensão admissível pelo critério
de Euler para os casos em que a esbeltez da haste possui um valor igual ou superior
a 106 e inferior pelo critério de vigas curtas e intermediárias recomendado pela
AISC.
Os cálculos da tensão admissível pelo critério de Euler consistem no cálculo
da tensão crítica pela Eq. (25) e posterior, o cálculo da tensão admissível pela Eq.
(26), onde se obtém os valores das tensões admissíveis mostradas pelo gráfico da
Figura 51.
Figura 51: Gráfico da tensão versus esbeltez pelo critério de Euler [12]
Também se realiza o dimensionamento pelo critério de vigas curtas e
intermediárias. Esse é obtido pelo cálculo da tensão crítica realizado pela Eq. (27),
cálculo do coeficiente de segurança pela Eq. (28), que varia conforme a esbeltez da
viga e o cálculo da tensão admissível pela Eq. (29), onde os resultados da tensão
admissível estão representados no gráfico da Figura 52.
66
Figura 52: Gráfico da tensão versus esbeltez pelo critério de vigas curtas e intermediárias [12]
Para calcular a tensão atuante na haste, utiliza-se a Eq. (1), os resultados
estão representados para cada esbeltez na Figura 51 e Figura 52, pois a tensão
varia conforme a posição do pantógrafo (pelo fato da força do cilindro
variar conforme a elevação). Como observa-se nas figuras, em nenhum dos critérios
a tensão atuante na haste ultrapassou a tensão admissível, atendendo os requisitos
do projeto, sendo o caso mais crítico para o atuador aberto, conforme pode se
verificar na Figura 51, onde a esbeltez ficou com valor de 152, a tensão admissível
em 44 N/mm² e a atuante na peça de 42 N/mm².
3.4 DIMENSIONAMENTO DA ARTICULAÇÃO CENTRAL C
3.4.1 Dimensionamento do eixo da articulação C
Escolhe-se o material SAE 1045 como material do eixo, pelo fato de ser um
material com um teor de carbono mais elevado, consequentemente possuindo uma
dureza superior e boa resistência a abrasão, que é necessário, pois o mesmo vai
deslizar sobre a bucha. O eixo também precisa ter um bom acabamento superficial
para diminuir o atrito entre ele e a bucha, especificado pelo fabricante da bucha
como menor de 0,4 µm, conforme mostrado no anexo C. O mecanismo possui duas
67
articulações centrais, então a força em C deve ser dividida por dois para realizar o
dimensionamento dessa. A montagem desse eixo será realizada conforme Figura
53, a partir da interpretação dessa, obtém-se o diagrama de corpo livre equivalente
na Figura 54. Esse será submetido a flexão e cisalhamento, porém em pontos
diferentes, pois a máxima tensão normal oriunda da flexão ocorre na extremidade do
diâmetro do eixo onde o cisalhamento é zero e a máxima tensão de cisalhamento
ocorre na região de linha neutra onde a tensão oriunda da flexão é zero, tendo que
calcular o eixo para os dois tipos de solicitação. Os dados utilizados para
dimensionamento estão mostrados na Tabela 7.
Figura 53; Geometria do eixo [12]
Figura 54: Diagrama de corpo livre do eixo da Figura 53 [12]
68
d = t = Diâmetro
L12
L13
σe
c = d/2
Tabela 7: Dados para dimensionamento do eixo C [12]
Dados
Valor
50 mm
60 mm
2 mm
370 MPa
25 mm
Inicialmente, realiza-se o cálculo da tensão de cisalhamento utilizando a Eq.
(5), portanto, é necessário calcular a metade da área da secção transversal do eixo
denominada como A’, conforme mostrado na Eq. (85).
A' =
50 ²π
= 981 ,75 mm ²
8
(85)
Posterior calcula-se o y pela Eq. (86).
y=
3
3
.r = .25 = 9,375 mm
8
8
(86)
A Inércia pela Eq. extraída do anexo B, resultando na Eq. (87).
I=
254 π
= 306796,875mm4
4
(87)
Agora consegue-se calcular o momento estático através da Eq. (6), obtendo o
valor mostrado na Eq. (88).
Q = 981,75mm ².9,375mm = 9203,9mm³
(88)
Então calcula-se a tensão de cisalhamento pela Eq. (5), resultando na tensão
da Eq. (89).
τ xy =
76340,5N.9 203,9mm³
= 45,8 N / mm ²
306796,875 mm 4 .50mm
(89)
Para comparar com o cálculo da tensão máxima, realizado na Eq. (89),
realiza-se o cálculo da tensão média, calculado como cisalhamento puro pela Eq.
(4) resultando na Eq. (90), representando uma diferença de 18 % na tensão.
69
τ med =
76340 ,5 N
= 38,88 N / mm ²
1963,5mm ²
(90)
Para realizar o cálculo da tensão normal precisa-se calcular a flexão no eixo,
essa é calculada pela Eq. (91).
Mf = 0,5.FC.(0,5.L12 + L13) = 0,5.152681N .(0,5.60mm + 2mm) = 2442895 Nmm
(91)
Então calcula-se a tensão normal pela Eq. (11), resultando nos valores da Eq.
(92)
σ=
M .c 2442895Nmm.25mm
=
= 199N / mm²
I
306796,875mm4
(92)
Para verificar se o eixo atenderá a aplicação, é necessário calcular a tensão
admissível para a flexão através da Eq. (20) e para o cisalhamento pela Eq. (21).
σ
adm
τ
adm
=
370 N/mm²
= 243,4N/mm²
1,52
(93)
213,5
= 140,46N/mm ²
1,52
(94)
=
Como a tensão normal e de cisalhamento está abaixo da tensão admissível, o
diâmetro escolhido suportará a carga. Observa-se que a tensão admissível está 44,4
MPa acima da tensão normal. Considerando isso, pode-se diminuir mais o diâmetro
do eixo, porém, o diâmetro calculado não se enquadraria em uma bitola comercial,
aumentando os custos.
3.4.2 Dimensionamento da bucha da articulação C
Escolheram-se
buchas
comerciais
por
terem
um
custo
atrativo
e
disponibilidade no mercado por vários revendedores de peças, não limitando o
cliente na compra das mesmas do fabricante do equipamento, agilizando a
manutenção do equipamento. As principais características das buchas adotadas DU
do fabricante GGB, são:
70
•
Material para aplicação a seco, com excelente propriedade de atrito e
desgaste em uma ampla faixa de condições de carga, velocidade e
temperatura.
•
São
aplicadas
na
indústria
aeroespacial,
equipamentos
agrícolas,
equipamentos de construção, equipamentos de manuseio de materiais,
máquinas de moldagem - metal, plástico e borracha; equipamentos de
escritório,
equipamentos
médicos
e
científicos,
equipamentos
para
embalagem, cilindros pneumáticos e hidráulicos, bombas e motores, ferrovias
e vias para trens elétricos, maquinário têxtil, válvulas, etc.
As propriedades mecânicas das buchas constam no anexo C, junto com
essas o fabricante recomenda a máxima tensão admissível devido ao tipo de
carregamento e número de ciclos desejados para o equipamento. Classifica-se a
aplicação em cargas dinâmicas com movimentos oscilatórios, onde a pressão adm.
para 100.000 ciclos é de 30 MPa, sendo adotado o valor de 100.000 ciclos pois
satisfaz um ano de operação do equipamento durante uma jornada de 24 h por dia.
Como o mecanismo possui duas articulações centrais, a força em C deve ser
dividida por dois para se realizar o dimensionamento da bucha mostrada
anteriormente como 01 na Figura 53. O dimensionamento da mesma será realizado
através da tensão de esmagamento da bucha pela Eq. (1), onde a área é a
projetada, calculada pela Eq. (7), onde t é a largura da peça representada por L12,
unem-se as Eq. (1) e (7) e isola-se L12, conforme mostrado na Eq. (95) onde se
obtém a largura mínima da bucha.
L12 =
0,5 .FC
76340 ,5 N
=
= 50 ,9 N / mm ²
d .σ adm 50 mm .30 N / mm ²
(95)
Obtém-se uma bucha com largura mínima de 50,9 mm, como essa medida
não é padrão comercial, escolhemos a bucha de maior largura mais próxima, sendo
a bucha de 60mm, aumentando a vida útil da mesma.
3.5 DIMENSIONAMENTO DA ARTICULAÇÃO LATERAL A
71
3.5.1 Dimensionamento da bucha A
Utiliza-se o mesmo modelo de bucha que foi utilizada na secão 3.4.2, porém
com as dimensões adequadas para os esforços que as mesmas serão submetidas
nos dois mancais da articulação A. Como são dois mancais, a carga de A será
dividida por dois. Essa bucha será dimensionada pela tensão de esmagamento
através da Eq. (1), onde a área é calculada pela Eq. (7), as Eq. são unidas e o
diâmetro é isolado conforme Eq. (96). Os dados utilizados nos cálculos estão
expressos na Tabela 8.
FA
L12
σadm
Tabela 8: Dados para dimensionamento da bucha da articulação A [12]
Dados
Valor
147912 N
*60 mm
30 N/mm²
(* )Mesma largura da articulação C, facilita a montagem.
d=
0,5.F A
73956 N
=
= 41mm
σ .L12
30 N / mm ².60 mm
(96)
Foi obtido um diâmetro de eixo de 41mm, levando em consideração que o
diâmetro comercial mais próximo é de 45 mm ou de 40 mm escolhe-se o de 40 mm,
pois a tensão vai aumentar para 30,8 N/mm², reduzindo sua vida útil, porém de
maneira insignifcativa.
3.5.2 Dimensionamento do eixo do mancal A
O eixo que fará a fixação do mancal A, também será construído com o
material SAE 1045, possuindo sua fixação de acordo com a mostrada na Figura 55
resultando no diagrama de corpo livre mostrado na Figura 56.
72
Figura 55; Geometria do eixo [12]
Figura 56: Diagrama de corpo livre para o eixo da articulação A [12]
Em um primeiro instante, interpreta-se que o diagrama resultante da Figura 55
seria engastado, não rotulado conforme mostra a Figura 56, porém após simulação
feita no software AutoCAD Mechanical mostrada no anexo D, nota-se que a
deformação do eixo na região do furo é muito pequena, sendo inferior a folga do furo
do suporte do eixo, então se comportando como uma rótula.
O eixo será submetido, a flexão e cisalhamento,sendo o local de maior tensão
à flexão, na metade da dimensão L14, possuindo a magnitude da tensão na
superfície externa, já a maior tensão provocada pelo cisalhamento acontecerá entre
o mancal 03 e o suporte 01 conforme mostra anteriormente Figura 55, onde seu
valor máximo ocorre no centro do eixo (linha neutra). Como ambas não acontecem
no mesmo ponto, serão avaliadas individualmente, conforme veremos a seguir.
Como calculado na seção 3.5.1, o diâmetro mínimo do eixo para o esmagamento da
73
bucha é de 40 mm, então faz-se os cálculos de tensão no eixo para ver se esse
resiste.
Tabela 9: Dados para dimensionamento do eixo da articulação A [12]
Dados
Valor
Diâmetro (d)
40 mm
0,5 Força em A (FA)
73956N
L12
60 mm
L14
65 mm
Força por unidade de comprimento (q)
73956 / 60 = 1232,6 N/mm
Reações RG = RH
73956 / 2 = 36978 N
Distância momento máximo (x)
32,5 mm
c=d/2
20 mm
Como a peça vai ser submetida à flexão e cisalhamento, o cisalhamento deve
ser calculado pela Eq. (5), para isto devemos calcular a A’ e y conforme descrito na
seção 1.1.2, esses são calculados conforme Eq. (97) e (98).
A' =
40 ²π
= 628 ,32 mm ²
8
(97)
y=
3
3
.r = .20 = 7 ,5 mm
8
8
(98)
Com base nos dados calculados anteriormente, consegue-se calcular o
momento estático através da Eq. (6), obtendo o valor mostrado na Eq. (99).
Q = 628,32mm ².7,5mm = 4712,4mm ³
(99)
Também calcula-se a inércia da secção transversal pela Eq. (100).
I=
204 π
= 125664mm4
4
(100)
Então, calcula-se a tensão de cisalhamento pela Eq. (5) Obtém-se a tensão
de cisalhamento da Eq. (101)
τ=
73956 N .4712,4 mm ³
= 34,7 N / mm ²
2.125664 mm 4 .40 mm
(101)
74
Verifica-se que a tensão de cisalhamento calculada pela Eq. (101) não
ultrapassou a tensão adm de cisalhamento calculada pela Eq. (94), então o diâmetro
de 40 mm atende pelo critério de cisalhamento. Agora, faz-se a verificação pelo
critério da tensão normal provocada pela flexão.
Como a carga está no centro da viga sabemos que o maior momento fletor
está no centro desta, então faz-se o cálculo do momento para esta posição. A
Figura 57 mostra o diagrama de corpo livre para cálculo do momento fletor pela Eq.
(103).
Figura 57: Diagrama de corpo livre [12]
 p.( x − 2,5mm) 2
M = ( RG .x) − 
2




 1232,6 N / mm.(32,5mm − 2,5mm)² 
M = (36978N .32,5mm) − 
 = 647115Nmm
2


(102)
(103)
Então, calcula-se a tensão oriunda do momento fletor pela Eq. (11), onde
obtém-se a tensão expressa pela Eq. (104).
σ =
647115 N .mm .20 mm
= 103 N / mm ²
125664 mm 4
(104)
Como a tensão calculada na Eq. (104) não ultrapassou a tensão admissível,
calculada pela na Eq. (93), o eixo vai resistir, como se pode perceber o diâmetro
poderia ser menor, pois a tensão no eixo está bem abaixo da tensão admissível.
Esse poderia ter diâmetro de 30 mm, que atenderia a tensão admissível, a tensão
normal e ao cisalhamento, porém causaria problemas na bucha, obrigando a utilizar
o diâmetro de 40 mm, ou aumentar largura do mancal, situação indesejada devido à
montagem do mecanismo.
75
3.5.3 Dimensionamento do mancal A
O mancal que acomodará a bucha será construído com um tubo sem costura.
Optou-se pelo material ST 52 (anexo E), que será soldado em um dos seus lados na
alavanca AE, conforme mostrado na Figura 58. Sendo assim, o mesmo vai ser
submetido a um esforço de tração, onde a área perpendicular a direção da força
deve suportar a carga da articulação A.
Também vai existir o esmagamento na face de contato do mancal com a
bucha, porém o material do mancal terá propriedades mecânicas superiores ao da
bucha, onerando o cálculo pelo fato da área já estar adequada para a situação
crítica de tensão de esmagamento da bucha. O dimensionamento da área
tracionada do mancal será realizado, com base nas características já dimensionadas
anteriormente mostradas na Tabela 10.
Tabela 10: Dados para dimensionamento do mancal A [12]
Dados
Valores
L12
60 mm
Diâmetro do eixo (d)
40 mm
Espessura da parede da bucha (t)
2 mm
Diâmetro interno (di)
44 mm
Diâmetro externo (de)
55,5 mm
0,5 Força em A (FA)
73956 N
σe (Anexo E)
345 MPa
Figura 58: Geometria do mancal [12]
Calcula-se a tensão nesse caso usando a Eq. (2), onde a área utilizada para o
cálculo é calculada pela Eq. (3), resultando no valor da Eq. (105).
76
A = (55,5 − 44)mm.60mm = 690mm²
(105)
Também necessita-se obter o concentrador de tensão. Este é obtido a partir
da interpretação da Figura 6 mostrada anteriormente, entrando com as relações
geométricas calculadas pelas Eq. (106) e (107). O fator de concentração (kt)
encontrado foi de 2,1.
Curva =
h 27 ,75 mm
=
= 0,5
w
55,5mm
Eixo _ horizontal =
di
44 mm
=
= 0,79
w 55,5mm
(106)
(107)
Com base nos dados obtidos anteriormente, conseguiu-se calcular a tensão
máxima no mancal conforme mostra a Eq. (108).
σ max =
73956N
.2.1 = 225N/mm ²
690mm²
(108)
Para verificar se o diâmetro escolhido atende os requisitos da norma, calculase a tensão admissível pela Eq. (20), obtendo o valor da Eq. (109).
σ
adm
=
343 N/mm²
= 225,7 N/mm²
1,52
(109)
Observa-se na Eq. (109), que a tensão atuante na peça calculada pela Eq.,
(108) é inferior a tensão admissível para o material utilizado, assim atendendo os
requisitos de resistência da norma utilizada.
3.6 DIMENSIONAMENTO DO EIXO E e B
Nas articulações E e B têm-se um rolo composto de rolamentos e uma capa
externa que é montada em cada extremidade do eixo, conforme pôde ser visto
anteriormente na Figura 33. O rolo se movimenta na horizontal conforme acontece a
elevação do pantógrafo, esse movimento causa um aumento na reação sobre o rolo
77
e consequentemente sobre o eixo, possuindo a magnitude de força quando o
pantógrafo estiver na elevação máxima. Esse pode ser exemplificado pela Figura 59,
onde a medida L13 permanece constante, assim como a força, gerando sempre o
mesmo momento sobre a placa (item 01), sendo a reação em E obtida pela divisão
do momento pela dimensão L11, sendo que o valor dessa está diminuindo conforme
a elevação do pantógrafo. A reação vai aumentando conforme mostrado pelo gráfico
da Figura 60, sendo a maior reação de 27826 N.
Figura 59: Diagrama de corpo livre equivalente [12]
Figura 60: Gráfico da variação da reação no eixo B e E, conforme elevação do mecanismo [12]
78
O eixo que acomoda o rolamento é engastado no tubo e soldado conforme a
Figura 61, este é submetido à flexão, sendo avaliado em dois locais, no menor e
maior diâmetro pelo fato de ambos serem submetidos a momentos diferentes. A
Força aplicada sobre cada eixo é a metade da reação em E e B, pelo fato de se ter
dois rolos.
Figura 61: Desenho representativo do eixo de suporte do rolo soldado nos tubos [12]
Para dimensionar o eixo, necessita-se calcular a inércia do mesmo pela Eq..
extraída do anexo B, resolvida na Eq. (110).
I=
12,54 π
= 19174,8mm4
4
(110)
Posteriormente, é obtido o concentrador de tensão através da Figura 21, vista
anteriormente, entrando com as relações geométricas calculadas pelas Eq. (111) e
(112).
Curva =
D 44,45mm
=
= 1,78
d
25mm
Eixo _ horizontal =
r
5mm
=
= 0,2
d 25mm
(111)
(112)
Obtém o kt= 1,4, então, calcula-se o momento fletor sobre o primeiro eixo,
esse é calculado pela Eq. (113).
M = 0,5.FE.x1 = 13913N .15mm = 208695Nmm
(113)
79
A tensão é calculada pela Eq. (13), resultando nos valores mostrados na Eq.
(114).
σ max =
208695Nmm. 12,5mm
.1,4 = 190,5 N/mm²
19174,8 mm 4
(114)
Para verificar se o material escolhido atende aos requisitos da norma, calculase a tensão admissível para o material escolhido, SAE 1020, que possui a tensão de
escoamento de 295 N/mm², conforme tabela do Anexo G. Essa é calculada pela Eq.
(20), resultando na tensão admissível da Eq. (115).
σ
adm
=
295 N/mm²
= 194N/mm²
1,52
(115)
Verifica-se que a tensão máxima não ultrapassou a admissível, sendo assim,
o eixo de diâmetro de 25 mm com raio de adoçamento de 5 mm atende os requisitos
de resistência.
Necessita-se calcular se o eixo suportará na região de maior momento e
maior diâmetro, localizada na união do mesmo com o tubo, conforme mostra
anteriormente a Figura 61. Para isso, calcula-se a inércia pela Eq. (116), o momento
fletor pela Eq. (117) e posteriormente a tensão média pela Eq. (118), calcula-se a
tensão média pelo fato de não conseguir mensurar analiticamente a concentração
de tensão para situação em questão.
I=
22,224 π
= 191627,6mm4
4
(116)
M = 0,5.FE.x2 = 13913N .92mm = 1279996Nmm
(117)
1279996Nmm .22,22mm
= 148,42N/mm ²
191627,6mm 4
(118)
σ med =
Após cálculo, verifica-se que o diâmetro de 44,45 mm atende os requisitos da
norma utilizada para dimensionamento. A tensão admissível do material é 30 %
maior que a atuante na peça, assim tendo uma segurança maior pelo fato de não ter
sido considerado o concentrador de tensão no cálculo.
80
3.7 DIMENSIONAMENTO DO TUBO DO SUPORTE DO CILINDRO
A força do atuador hidráulico é transmitida através de um tubo 7 mostrado
anteriormente na Figura 35, esse possui a secção circular pelo fato de ser submetido
a um elevado torque, pois as secções circulares possuem um desempenho superior
à torção, que os tubos com secção quadrada. Os dados utilizados para o
dimensionamento do mesmo estão expressos na Tabela 11.
Tabela 11: Dados para dimensionamento do tubo [12]
Dados
Valores
78 mm
56 mm
225,7 N/mm²
72 mm
1029 mm
150 mm
39 mm
Diâmetro externo (de)
Diâmetro interno (di)
σadm= EQ (109)
L15
L16
L17
c = D/2
Como pode se verificar no digrama de corpo livre da Figura 62, o eixo é
engastado nas duas extremidades e é submetido ao esforço torçor e à flexão, o
torque é calculado pela Eq. (119), onde a dimensão L17 está representada
anteriormente pela Figura 40 e é aplicada somente a metade da força do atuador
devido a dois dos quatro suportes estarem soldados nas alavancas não gerando
torção nem flexão ao tubo.
Figura 62: Diagrama de corpo livre [12]
T = (0,5.FCil .L17 ) / 2 = (76340,5 N .150mm) / 2 = 5725537,5 Nmm
(119)
81
Calcula-se a inércia polar pela Eq. (10), sendo o resultado representado na
Eq. (120).
J=
39mm4 π 28mm4 π
−
= 2668445,2mm4
2
2
(120)
Então calcula-se a tensão atuante na peça pela Eq. (8), resultando na tensão
expressa pela Eq. (121).
τ = 5725537,5N mm.39mm = 83,7 N/mm²
2668445,2m m 4
(121)
O diagrama representado pela Figura 62 é estaticamente indeterminável. O
cálculo do momento fletor para este é bastante trabalhoso, então se opta em
calcular o mesmo pelo Software AutoCAD Mechanical. Conforme pode ser visto no
Anexo H, o resultado obtido foi um momento de 2.555.900 Nmm.
Calcula-se a inércia de área do tubo pela Eq. (122).
I=
J
= 1334222,6mm4
2
(122)
Então é realizado o cálculo da tensão normal no tubo pela Eq. (11), e obtêmse os resultados expressos pela Eq. (123).
σ=
2555900Nmm .39mm
= 74,7N/mm²
1334222,6m m 4
(123)
Como essa peça possui tensão normal e de cisalhamento no mesmo ponto,
temos que calcular a tensão equivalente para os dois estados de tensão pelo critério
de von Mises. Para chegar ao resultado deve-se calcular primeiro a σmax= σ1 pela Eq.
(14) e σmin= σ3 pela Eq. (15), então calcula-se a tensão de von Mises pela Eq. (16),
resultando na tensão expressa pela Eq. (124).
σ
VM
= 129²− (129.- 54,3)+ (-54,3)²=163,1N/mm²
(124)
82
Verifica-se que o eixo está atendendo os critério de segurança exigido pela
norma, pois a tensão de von Mises da Eq. (124) está abaixo da tensão admissível da
Eq. (109).
3.8 DIMENSIONAMENTO DA BARRA AE
A barra AE mostrada na Figura 63 pode ser considerada como uma viga pelo
fato da mesma possuir uma força perpendicular ao seu comprimento. Esta viga está
rotulada na articulação A e C, sendo submetida a força FE,y, no ponto E e um
momento fletor em yy que é transmitido pelo eixo da articulação C .
Escolhem-se dois perfis para formar cada barra estes possuem a secção
tubular retangular pelo fato do mesmo possuir maior inércia com menor massa
quando comparados com perfis retangulares maciços, na
Tabela 12 constam os dados necessários para realizar o dimensionamento das
barras AE e BD.
Tabela 12: Dados para dimensionamento das barras [12]
Dados
Valores
Altura externa do tubo (he)
150 mm
Largura externa do tubo (be)
50 mm
Altura interna do tubo (hi)
137,3 mm
Largura interna do tubo (bi)
37,3 mm
θ1
5,82°
θ3
24,8°
L1
2210 mm
L2
1105 mm
L18
389 mm
F D= F E
17500 N
c1
75 mm
c2
25 mm
Obs: Os cálculos serão realizados considerando somente metade da carga e um dos
dois perfis iguais que compõem cada barra (conjunto alavanca, Figura 34).
83
Figura 63: Diagrama de corpo livre da barra AE [12]
Para realizar o dimensionamento da barra AE inicialmente calcula-se o
momento fletor formado pela força FE através da Eq. (125).
M xx = 0,5.FE . cos θ 1°.L2 = 8750 N . cos 5,82 .1105 mm = 9618911 ,2 Nmm
(125)
Posteriormente, calcula-se a inércia em xx através da Eq. extraída do anexo
B resultando nos valores da Eq. (126).
I
xx
=
1503.50 137,33.37,33
−
= 6017256mm4
12
12
(126)
Então calcula-se a tensão normal xx pela Eq. (11) obtendo a tensão da Eq.
(127).
σ xx =
9618911,2N mm.75mm
= 119,9N/mm²
6017256mm 4
(127)
Em seguida calcula-se a inércia em yy através da Eq. extraída do anexo B
resultando nos valores da Eq. (128).
I =
yy
503.150 37,333.137,3
−
= 968733mm4
12
12
(128)
Então calcula-se a tensão normal yy pela Eq. (11), onde o momento atuante
na direção yy é transmitido pelo eixo da articulação C para a barra AE calculado
anteriormente na Eq. (91) resultando nos valores da Eq. (129).
84
σ yy =
2442896Nmm .25mm
= 63N/mm²
7968733mm 4
(129)
Como se tratam de tensões combinadas temos que calcular a tensão de von
Mises. Para chegar ao resultado, deve-se calcular primeiro o σmax= σ1 pela Eq. (14)
e σmin= σ3 pela Eq. (15), então calcula-se a tensão de von Mises pela Eq. (16),
resultando no valor da Eq. (130).
σ
VM
= 120²− (120. - 63,1)+ (-63,1)²=161,1.N/mm²
(130)
Posteriormente se calcula a tensão admissível para o material do tubo VHB
250 do anexo I, este é realizado através da Eq. (20), resultando no valor da Eq.
(131).
σ adm =
250 N/mm²
= 164,5N/mm²
1,52
(131)
Como se pode verificar, a tensão atuante na peça calculada pela Eq. (130)
está abaixo da tensão admissível do material, mostrada pela Eq. (131), assim
atendendo os requisitos de segurança do dimensionamento exigido pela norma.
3.9 DIMENSIONAMENTO DA BARRA BD
A barra BD mostrada na Figura 64 é submetida ao mesmo momento fletor da
barra AE na sua região central onerando o cálculo desta pois ambas são
construídas com o mesmo perfil, então possuem a mesma inércia, porém a barra BD
vai possuir o suporte do atuador fixo sobre ela, conforme mostra anteriormente a
Figura 35, devido à geometria do suporte, o mesmo provoca uma variação brusca na
geometria do conjunto, assim formando um concentrador de tensão, que pelo fato de
não ser de nem uma geometria clássica não conseguimos determiná-lo
analiticamente, então calcula-se a tensão nesta região sem considerar o
concentrador de tensão que será obtido nos cálculos numéricos.
85
Figura 64: Diagrama de corpo livre da barra BD [12]
Inicialmente calcula-se o momento fletor na viga pela Eq. (132),
M xx = 0,5.F D. cosθ1 °.( L2 − L18 ) = 8750N . cos .5,82°.(1105mm − 389mm) = 6232706,25Nmm
(132)
Então calcula-se a tensão normal xx pela Eq. (11), onde obtêm-se os valores
na Eq. (133).
σ xx =
6232706,25 Nmm.75mm
= 77,7N/mm²
6017256mm 4
(133)
Então calcula-se a tensão normal yy pela Eq. (11), onde o momento atuante é
de 2555900 Nmm transmitido pelo tubo suporte do cilindro à barra BD resultando
nos valores da Eq. (134).
σ yy =
2555900Nmm .25mm
= 66N/mm²
968733mm 4
(134)
Como se tratam de tensões combinadas, temos que calcular a tensão de von
Mises. Para chegar ao resultado, deve-se calcular primeiro o σmax= σ1 pela Eq. (14)
e σmin= σ3 pela Eq. (15), então calcula-se a tensão de von Mises pela Eq. (16),
resultando no valor da Eq. (135).
σ
VM
= 77,7²− (77,7. - 66)+ (-66)²=124,5.N/mm²
(135)
86
Como a tensão máxima da Eq. (135) não ultrapassou a tensão adm da Eq.
(131) o tubo atende as exigências da norma.
3.10 CÁLCULO DO SUPORTE DO CILINDRO
O atuador é fixo em quatro suportes conforme pôde ser visto anteriormente na
Figura 33, este será dimensionado pela tensão normal provocado pela flexão, onde
o ponto de maior momento sobre o suporte será nas proximidades do tubo conforme
mostra a Figura 65, que coincide com o corte da secção transversal. Além da flexão,
avalia-se a tensão normal provocada pelo esmagamento no furo. Os cálculos são
realizados com os dados da Tabela 13.
Tabela 13: Dados para dimensionamento do suporte do atuador [12]
Dados
Valores
Altura da chapa (h)
118 mm
Largura da chapa (b)
12,7 mm
Diâmetro do furo (d)
40 mm
0,25FCil
38170 N
θ4
27,4°
x
130 mm
c
59 mm
250 N/mm²
σe(ASTM A36)
Figura 65: Suporte do cilindro [12]
Inicialmente calcula-se a inércia da secção transversal pela equação extraída
do anexo B, resultando no valor da Eq. (136).
87
I
xx
=
h3.b 1183.12,7
=
= 1738875,5mm4
12
12
(136)
Posteriormente é calculado o momento formado pela força perpendicular à
secção da inércia pela Eq. (137).
M xx = 0,25 .FCil . cos θ 4 °.x = 38170 N . cos 27 ,4.130 mm = 4405428 ,7 Nmm
(137)
Então se calcula a tensão normal provocada pelo momento fletor através da
Eq. (11) resultando no valor da Eq. (138), porem foi desconsiderado a tensão normal
axial provocada pela força Fx.
σ xx =
4405428,7N mm.59mm
= 149,5N/mm²
1738875,5m m 4
(138)
A tensão de esmagamento é calculada através da Eq. (1) resultando na
tensão média expressa pela Eq. (139)
σ
med
=
38170 N
= 75N/mm ²
40.12,7
(139)
Então se calcula a tensão admissível pela Eq. 20, onde se obtém o valor da
mesma na Eq. (140).
σ
adm
=
250 N/mm ²
= 164,5 N/mm ²
1,52
(140)
Como se verifica, as tensões atuantes no suporte, expressas pelas EQ. (138)
e (139) não ultrapassam a tensão admissível expressa pela EQ. (140), assim
atendendo os requisitos de segurança no dimensionamento exigido pela norma.
3.11 RESULTADOS OBTIDOS NOS CÁLCULOS ANALÍTICOS
88
Para melhorar a visualização dos resultados obtidos nos cálculos analíticos os
mesmos foram expostos na Tabela 14.
Tabela 14: Resultados do dimensionamento analítico [12]
Item
Diâmetro do atuador
Dimensão [mm]
θ 76,2
Material
-
Diâmetro da haste do
atuador
θ 35
SAE 1045
Diâmetro do eixo A
θ 40
SAE 1045
Bucha do mancal A
θ 40 x θ 44 x 60
DU
θ 55,5 x θ 44 x 60
ST 52
Diâmetro menor do eixo B
θ 25
SAE 1020
Diâmetro maior do eixo B
θ 44,45
SAE 1020
Diâmetro do eixo C
θ 50
SAE 1045
Bucha do mancal C
θ 55x θ 50 x 60
DU
θ 66,5 x θ 55 x 60
ST 52
θ 40
θ 44 x θ 40 x 60
SAE 1045
DU
θ 55,5 x θ 44 x 60
ST 52
Diâmetro menor do eixo E
θ 25
SAE 1020
Diâmetro maior do eixo E
θ 44,45
SAE 1020
θ 78 x θ 56
ST 52
Mancal A
Mancal C
Diâmetro do eixo D
Bucha do mancal D
Mancal D
Tubo do suporte do cilindro
Observação
Pressão de 167 bar no atuador
Dimensionada considerando que
o atuador possui a mesma inércia
da haste em toda sua extensão.
E eixo cromado para reduzir o
atrito.
Eixo cromado para atender a
rugosidade mínima da bucha de
0,4 µm.
Dimensionado para suportar a
carga máxima durante 100.000
ciclos.
Tubo sem costura.
Diâmetro
do
assento
do
rolamento, considerando que o
mesmo terá um raio de
adoçamento de 5 mm
Eixo cromado para atender a
rugosidade mínima da bucha de
0,4 µm.
Dimensionado para suportar a
carga máxima durante 100.000
ciclos.
O mancal C tem 3,2 % a mais de
força que o mancal A, porem é
engastado
em
toda
sua
circunferência
no
tubo,
reforçando o mesmo. Adota-se a
mesma parede do tubo utilizado
na articulação A.
A articulação D será submetida a
uma carga inferior a do mancal A,
porem
por
motivo
de
padronização de peças (reduzir
tempo de manufatura) adota-se o
mesmo eixo, bucha e mancal da
articulação A.
Será submetido a mesma força
da articulação B, então onera-se
o cálculo e adota-se o mesmo
diâmetro.
Será submetido ao mesma força
da articulação B, porem possui
um comprimento menor em
balanço (gera menor momento),
podendo reduzir o diâmetro do
eixo, porem por padronização
adota-se o mesmo diâmetro
maior da articulação B.
Dimensionado sem considerar os
concentradores de tensão, pois
89
Tubo da alavancas AE
Alt.150 x Larg. 50 x
Esp. 6,35
Tubo da alavancas BD
Alt.150 x Larg. 50 x
Esp. 6,35
Suporte do atuador
Alt.118 x Esp.12,7
não se tratam de casos típicos.
Dimensionado com tubos pelo
fato dos mesmos possuírem
maior inércia com menos massa,
se comparados com perfis
formados com barras maciças.
A tensão do tubo BD na região
central é a mesma do tubo AE,
porem na região em que o
suporte do cilindro é unido com o
tubo BD terá uma concentração
de tensão não calculada por não
se tratar de um caso clássico.
ASTM A36
90
4 SIMULAÇÃO NUMÉRICA PELO MÉTODO DOS ELEMENTOS FINITOS
Neste capitulo será desenvolvido os cálculos em elementos finitos do
mecanismo pantográfico desenhado com as dimensões obtidas através dos cálculos
da seção 3, sendo este implementado pelo software Ansys, os passos realizados
para elaborar os mesmos estão expressos no fluxograma da Figura 66.
Figura 66: Fluxograma dos passos das análises em elementos finitos [12]
91
4.1 SIMULAÇÃO NUMÉRICA DE FLAMBAGEM DA HASTE DO CILINDRO
Neste capítulo, faz-se a simulação numérica da flambagem da haste do
atuador dimensionado analiticamente na seção 3.3.2. Os softwares utilizados para
realizar a mesma foi o de CAD Solid Works 2010 para desenhar as peças e o de
MEF foi o Ansys Workbench 12.1, módulo Linear Buckling, atribuindo as condições
de rotulado nas duas extremidades e aplicando a Força de 40232 N para o
comprimento de 1334 mm (pior situação encontrada nos cálculos analíticos).
A primeira simulação foi realizada considerando o atuador como sendo uma
barra de secção uniforme com o diâmetro da haste, de 35 mm, conforme
considerado no dimensionamento analítico. A malha gerada possui 13.108 nós e
6.712 elementos, resultando na deformação e fator de carga mostrada na Figura 67.
Sendo o fator de carga (Load Multiplier) de 2,07. Temos esse como fator de
segurança. Comparando o fator de segurança com o do cálculo analítico, tem-se um
aumento de 8 % no coeficiente de segurança considerado no cálculo analítico,
atendendo os requisitos da norma.
Figura 67: Resultados da Simulação Numérica da Haste [12]
92
Como a geometria foi simplificada considerando a pior hipótese, devido aos
recursos de cálculos analíticos disponíveis, a situação simulada anteriormente não
corresponde a situação de geometria real de um atuador linear hidráulico, então
modela-se o mesmo com a sua geometria do atuador completo, considerando que o
mesmo tenha a haste e camisa unidas e realizam-se os cálculos com mesmas
condições de contornos aplicadas no cálculo anterior, onde utiliza-se uma malha
com 33.318 nós e 16.954 elementos e obtém-se a deformação e fator de carga
mostrada na Figura 68. Sendo o fator de carga de 4,14, verifica-se que o atuador
hidráulico está com um coeficiente de segurança maior do que o exigido pela norma.
Figura 68: Resultados da Simulação Numérica do Atuador [12]
4.2 SIMULAÇÃO NUMÉRICA DO PANTÓGRAFO
Esta seção mostra a simulação numérica das alavancas do pantógrafo
através do software Ansys Workbench 12.1, no módulo Static Structural e os
resultados obtidos.
93
Para realizar a simulação, desenha-se o mecanismo abaixado no software de
CAD Solid Works 2010, com as dimensões obtidas através do dimensionamento
analítico, o mecanismo é simétrico então simplifica-se o cálculo desenhando
somente metade do mecanismo e atribuindo a condição de contorno de simetria que
considera o comportamento do mecanismo como um todo, agilizando o cálculo do
mesmo. As condições de contorno do mecanismo estão expressas na Figura 69,
onde:
1) Cylindrical Support (permite o movimento tangencial e fixo nas demais
direções);
2) Remote Displacement (restrito na direção y e livre nas demais direções);
3) Joint cilíndrica (permite o movimento tangencial e fixo nas demais direções);
4) Remote Displacement (restrito na direção x e y e livre nas demais direções);
5) Força na direção y de 8750 N (metade da força da articulação E, pelo fato de
ser somente um lado do pantógrafo);
6) Força de um atuador hidráulico de 76340,5 N distribuída nos dois olhais,
resultando na força em x de 36091 N e em y de 12427 N para cada olhal;
7) Face de simetria;
Figura 69: Condições de contorno do mecanismo pantográfico abaixado [12]
Após gera-se a malha com 83.715 nós e 45.633 elementos resultando no
mapa de tensões da Figura 70 e no mapa de deformações da Figura 71.
94
Figura 70: Mapa de tensão do pantógrafo abaixado [12]
Figura 71: Mapa de deformações do pantógrafo abaixado [12]
95
4.2.1 Tensões na barra AE
A Figura 72 e Figura 73 mostram o mapa de tensões de maior intensidade na
barra AE, que possui a máxima tensão de 160,07 N/mm² (MPa), compara-se essa
com a calculada analiticamente na seção 3.9, que resultou na tensão de 161,1
N/mm², verifica-se que o cálculo numéricos chegou praticamente no mesmo
resultado do analítico.
Barra AE
Figura 72: Mapa de tensões da barra AE (vista superior) [12]
Barra AE
Figura 73: Mapa de tensões da barra AE (vista inferior) [12]
96
4.2.2 Tensões na barra BD
A Figura 74 e Figura 75 mostram o mapa de tensões de maior intensidade da
barra BD, essa é submetida aos mesmos esforços da barra AE na sua região central
(nas proximidades da articulação C), porém a barra BD possui um dos suportes do
atuador soldado em seu corpo gerando assim um concentrador de tensão pela
descontinuidade da geometria, o cálculo numérico resultou em uma tensão de 184,4
N/mm² conforme a Figura 76, sendo a tensão calculada analiticamente de 124,5
N/mm², essa é encontrada na região mais afastada da descontinuidade.
Barra BD
Figura 74: Mapa de tensões da barra BD (vista superior) [12]
Barra BD
Figura 75: Mapa de tensões da barra BD (vista inferior) [12]
97
Barra BD
Figura 76: Região de concentração de tensão da barra BD [12]
A transição do suporte gerou um concentrador de tensão de 1,5, assim
ultrapassando a tensão admissível para o material do tubo, para resolver este problema
verificam-se quatro opções: 1) Reforçar a região de concentrador com uma chapa de
envolvendo o tubo; 2) Colocar um tubo com propriedades mecânicas superior, 3) Fazer uma
solda que dê continuidade entre o suporte e tubo, com um ótimo acabamento superficial ou
4) Não soldar o suporte no tubo BD, porém aumentaria o torque sobre o tubo de secção
circular, tendo que aumentar seu diâmetro.
4.2.3 Tensões no suporte do atuador
A Figura 77 mostra o mapa de tensões do suporte do atuador, no qual verifica-se a
tensão próxima ao tubo com uma faixa de 149 N/mm² a 176 N/mm², possuindo um aumento
comparado com o cálculo analítico de 18 % que resultou na tensão de 149,5 N/mm², pelo
fato de não ter sido considerado a força axial.
Na região do furo, a tensão de esmagamento calculada através do método numérico
teve um aumento de 290 % (kt 2,9) comparado com o cálculo analítico da tensão média,
98
julga-se este ao concentrador de tensão que não foi avaliado no método analítico. Visto que
o valor da tensão atuante ultrapassou a tensão admissível tem-se várias opções para deixar
o suporte mais reforçado, sendo algumas destas: 1) Aumentar a espessura da chapa, 2)
Aumentar o diâmetro do furo (não indicado pois vai super dimensionar o eixo), 3) Substituir o
material por outro com maior tensão de escoamento ou 4) Soldar um reforço de secção
circular somente na região do furo aumentando sua espessura localmente (somente no local
necessário).
Suporte
Figura 77: Mapa de tensões no suporte do atuador [12]
4.2.4 Tensões no tubo circular
A Figura 78 mostra o mapa de tensões no tubo de secção circular, nesse verifica-se
que a tensão obtida no cálculo analítico 163,1 N/mm² confere com a tensão do cálculo
numérico encontrada na face perpendicular à força aplicada no suporte, porém na Figura 79
verificam-se tensões 35 % superior entre os suportes, julga-se que essa divergência esteja
acontecendo pelo fato da tensão calculada analiticamente ser válida somente para as faces
afastadas do local de aplicação do torque. Mesmo assim, a tensão atuante no tubo não
ultrapassou a admissível, atendendo as exigências da norma.
99
Tubo circular
Figura 78: Mapa de tensão no tubo circular [12]
Tubo circular
Figura 79: Mapa de tensão no tubo circular [12]
4.2.5 Tensões no mancal A
A Figura 80 mostra o mapa de tensão do mancal da articulação A, como se pode
verificar, a tensão máxima neste, ocorre na face interna do mancal na região perpendicular à
força aplicada, onde a máxima tensão resultante do cálculo numérico foi de 215,56 N/mm²
100
(MPa) que é inferior ao resultado obtido pelo cálculo analítico, que foi de 225 N/mm², julgase o decréscimo na tensão ao reforço formado pela tampa do tubo mostrada como 01 na
Figura 80.
01
Mancal A
Figura 80: Mapa de tensão do mancal A [12]
Mancal A
Figura 81: Mapa de tensões do mancal A [12]
101
4.2.6 Tensões no eixo B e E
O mapa da tensão na articulação B e E para a posição abaixada está representada
na Figura 82, nesta posição a tensão não possui sua maior magnitude, pois é o instante que
a articulação B e E possui menor força, sendo a posição elevada a mais crítica para o eixo
pela maior reação na articulação.
Eixo E
Eixo B
Figura 82: Mapa de tensões no eixo da articulação B e E (pantógrafo abaixado) [12]
Para verificar a tensão máxima no eixo da articulação B e E, realizam-se os cálculos
para a posição elevada conforme mostra anteriormente a Figura 38, sendo aplicadas as
mesmas condições de contorno mostradas anteriormente na Figura 69, porém aplicando as
cargas respectivas para a posição, sendo essas em 5) Força de 27826 N e 6) Força de
40232 N, sendo em x 15720 N e em y 37034 N, resultando no mapa de tensões mostrado
102
na Figura 83 e Figura 84. A Figura 83 mostra a tensão máxima no eixo da articulação E,
sendo a tensão máxima de 162,52 N/mm² (MPa) que ocorre no raio de transição dos
diâmetros do eixo.
Eixo E
Figura 83: Mapa de tensões no eixo E para o mecanismo elevado [12]
A Figura 84 mostra o mapa de tensão do eixo B, onde a tensão no raio de
transição é de 163,57 N/mm² (MPa) e a tensão máxima do eixo que ocorre na região
que o mesmo fica engastado com o tubo é de 192,85 N/mm² (MPa).
Eixo B
Figura 84: Mapa de tensões no eixo B para o mecanismo elevado [12]
103
Como se verifica na Figura 83 e Figura 84, a tensão obtida no raio de
adoçamento foi 18 % a menos que no cálculo numérico, essa diferença acontece
pelo fato de não possuir a curva de concentrador de tensão exata para as relações
geométricas da peça, assim escolhe-se a curva de maior valor mais próxima que
resulta em um concentrador de tensão superior ao real. Já no maior diâmetro se
obteve um aumento de 30 %, esse ocorreu pois a tensão calculada foi a média pelo
fato de não conseguir se obter o concentrador de tensão de forma analítica, o
concentrador de tensão obtido através do cálculo numérico para essa geometria foi
de 1,3. Mesmo com o acréscimo na tensão atuante na peça essa não ultrapassou a
tensão admissível do material atendendo os requisitos da norma.
104
CONCLUSÃO
Com a metodologia utilizada para dimensionar o mecanismo pantográfico,
conseguiu-se realizar um dimensionamento que garante a eficiência do mesmo, sem
a necessidade de atribuir grandes coeficientes de segurança devido à certeza dos
resultados obtidos através da metodologia utilizada, assim resultando em um
mecanismo pantográfico mais leve e barato.
Durante o desenvolvimento do trabalho foram utilizados dois métodos de
cálculos, o primeiro se trata da resistência dos materiais clássica, resolvida através
de cálculos analíticos e segundo se trata de cálculos numéricos realizados através
do método de elementos finitos implementado através do software Ansys 12.1. A
primeira metodologia foi utilizada para realizar o pré-dimensionamento do
mecanismo e a segunda para amparar o mesmo, pois devido à complexidade de
algumas peças estas não podem ser resolvidas de maneira exata através de
cálculos analíticos.
Para realizar o dimensionamento do mecanismo foi realizado a revisão
bibliográfica de resistência dos materiais clássica, onde os conteúdos da mesma
foram expressos resumidamente de maneira clara e objetiva, facilitando a
compreensão do mesmo para o leitor. Também foi realizado a revisão da teoria dos
elementos finitos, está foi feita através de um exemplo de cálculo simples e dos
procedimentos e cuidados para se realiza um cálculo em um software de MEF.
Os resultados obtidos através dos métodos analíticos e numéricos para as
peças com geometria simples tiveram pequena divergência entre os resultados,
porém nos casos mais complexos houve uma diferença superior. Pode-se citar o
caso da barra BD que tinha um suporte soldado em sua lateral provocando um
105
concentrador de tensão que não foi possível calcular através de cálculos analíticos
por não se tratar de um caso clássico, assim causando uma divergência de 150 %
em um ponto em específico.
Sendo assim, com os resultados encontrados nos métodos, consegue-se
elaborar uma planilha para dimensionamento dos mecanismos pantográficos, que
contemple os fatores de concentração não mensurados antes, dispensando o
dimensionamento numérico, assim agilizar o desenvolvimento de mecanismos
pantográficos com dimensões especiais, além de poder ser feito por mão-de-obra
menos qualificada, pois o projetista só necessita alimentar os dados de entrada para
obter o dimensionamento do equipamento, não precisa ter conhecimento do método
usado.
Deixo como sugestões para trabalhos futuros:
•
A realização dos cálculos dinâmicos do mecanismo (pois agora conhecemos
as massas e dimensões das peças) para comparação com os fatores
recomendados pela norma EN 1570-1998.
•
A Realização dos cálculos de fadiga das regiões criticas para comparar com o
coeficiente de segurança recomendado pela norma EN 1570-1998.
•
Validação experimental dos cálculos com o uso de extensometria.
106
REFERÊNCIAS
[1] BEER, Ferdinand; JOHNSTON, Russel. Resistência dos Materiais. 3° edição,
São Paulo: Pearson Makron Books, 1995.
[2] ENGBRASIL. Aula de Resistência dos Materiais. Disponível em:
<http://www.engbrasil.eng.br/pp/res/aula5.pdf>Acesso em 03/12/2011.
[3] SHIGLEY, Joseph E.; MISCHKE, Charles R. Standard Handbook of Machine
Design. 2° edição, EUA: McGraw-Hill, 1996.
[4] Norma NF_EN_1570_1998, Safety Requirements for Lifting Tables.
[5]AGENCIABRASIL. Déficit no faturamento de indústrias de máquinas e
equipamentos. Disponível em: <http://agenciabrasil.ebc.com.br/noticia/2011-0525/aumento-de-importacoes-faz-faturamento-da-industria-de-maquinas-eequipamentos-despencar> Acesso em 04/12/2011.
[6] NORTON, Robert L.. Projeto de Máquinas. 2° edição, Porto Alegre: Bookmann,
2004.
[7] ASSAN, A. Ernesto. Método dos Elementos Finitos Primeiros Passos. 1ª
edição. Campinas/SP. Editora Unicamp, 1999.
107
[8] DEMAR. Método de elementos finitos. Disponível em:
<http://www.demar.eel.usp.br/metodos/mat_didatico/Metodo_dos_Elementos_Finitos
.pdf>. Acesso em 21/12/2011.
[9] JUNGBECK, Marcelo R. Dimensionamento de uma estrutura metálica para
transporte de grãos através do método de elementos. Trabalho de Conclusão de
Curso. Universidade Regional do Noroeste do Estado do Rio Grande do Sul –
UNIJUÍ, Panambi – 2002.
[10] HAMMES, Daniel P. Projeto de estrutural para melhoria dos braços de uma
garra hidráulica com deslocamento. Trabalho de Conclusão de Curso.
Universidade Regional do Noroeste do Estado do Rio Grande do Sul –UNIJUÍ,
Panambi – 2004.
[11] WEHRMANN, Tiago R. Comparação de cálculos estruturais analíticos com
elementos finitos com diferentes malhas. Trabalho da disciplina de Projeto de
Conclusão de Curso. Universidade Regional do Noroeste do Estado do Rio Grande
do Sul –UNIJUÍ, Panambi – 2010.
[12] WEHRMANN, Tiago R. Desenhos no Software Auto CAD e SolidWorks, tabelas,
gráficos e cálculos em elementos finitos no software Ansys Workbench 12.1.
[13]
MOTOM.
Imagens
de
Plataformas
Elevatórias.
Disponível
<http://motam.com.br/>Acesso em 22/12/2011
[14] CASCADE. Imagens de PuchPull. Disponível em:
<http://www.cascorp.com/americas/en/mark55pushpull>Acesso em 22/12/2011
[15] Computador usado nos cálculos de elementos finitos: Notebook Dell Inspiron
com processador core™ 2 duo CPU T6600 @ 2,20HGz, Memória RAM 3 GB
em:
108
ANEXO A - Propriedades do aço SAE 1045 cromado
109
ANEXO B – Equações algébricas dos momentos de inércias de geometrias
comuns
Retângulo
y
y´
3
bh
bh 3
Ix´=
Ix =
12
3
.
h
x´
x
Iy´=
b3h
b3h
Iy =
12
3
Jc =
bh
bh 2
⋅ b 2 + h 2 Jo =
b + h2
12
3
Triângulo Isósceles/Eqüilátero
Ix´=
bh 3
bh 3
Ix =
36
12
Iy´=
b3h
b3h
Iy =
36
12
Jo =
bh
⋅ b2 + h2
12
b
y
y
h
.
x´
y´
.
h
x´
x
x
b
b
(
)
(
)
)
Círculo
y´
R
Ix´=
.
(
π ⋅ R4
4
Iy´=
π ⋅ R4
4
x´
Jo =
π ⋅ R4
2
Semicírculo
y
Ix =
.
π ⋅ R4
8
Iy =
π ⋅ R4
8
x
R
Jo =
π ⋅ R4
4
Quarto de Círculo
y
Ix =
.
π ⋅ R4
16
x
R
Jo =
Iy =
π ⋅ R4
8
π ⋅ R4
16
110
ANEXO C – Propriedades das buchas Du do fabricante GGB
111
ANEXO D – Simulação de deformação do eixo no software AutoCAD
Mechanical
Obtém-se a deformação máxima conforme mostra a tabela Max Deflexion =
0,0108 mm, também obtém-se a deformação do eixo dentro do furo do olhal com
espessura de 13 mm, sendo de 7,27/Scale for Defl Line= 7,27/1055,2 = 0,0069 mm,
sendo inferior a folga do furo, que possui o diâmetro de 40 0,03
com as respectivas
0,01 mm
tolerâncias, assim fazendo com que este seja considerado como rotulado conforme
a Figura 56.
112
ANEXO E – Propriedades do tubo ST 52
113
ANEXO F – Dimensões dos tubos ST 52
Obs: No dimensionamento do Mancal A, foi utilizado o Tubo de Diâmetro nominal de
56 mm, porém adotado para cálculo o diâmetro de 55,5 mm, que se refere ao
diâmetro garantido após a usinagem.
114
ANEXO G – Propriedades mecânicas dos aços nas condições laminados
normalizados e recozidos
115
116
ANEXO H – Cálculo do momento fletor no software AutoCAD Mechanical
Como se verifica na tabela, o tubo é submetido ao momento de 2.555.900
Nmm.
117
ANEXO I – Propriedades e dimensões dos tubos Dagan
118
ANEXO J – Propriedades de chapas de aço (Metalgusa)