Exercício 13) (0,5) Ao financiar uma casa no total de 20 anos

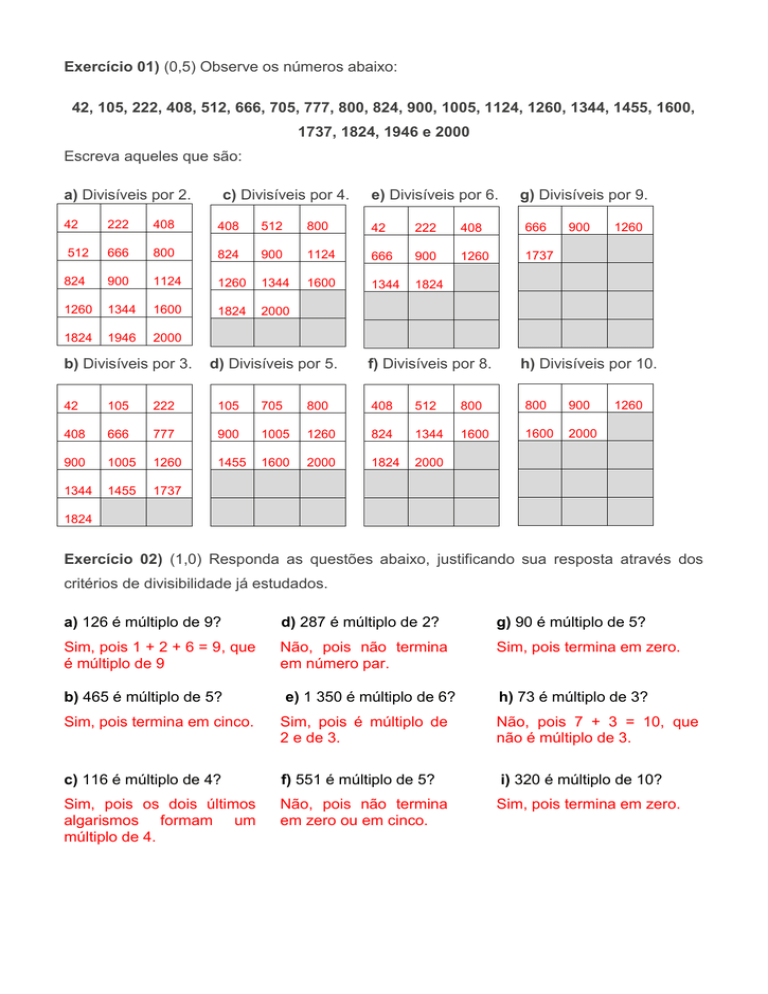
Exercício 01) (0,5) Observe os números abaixo:
42, 105, 222, 408, 512, 666, 705, 777, 800, 824, 900, 1005, 1124, 1260, 1344, 1455, 1600,
1737, 1824, 1946 e 2000
Escreva aqueles que são:
a) Divisíveis por 2.
c) Divisíveis por 4.
e) Divisíveis por 6.
g) Divisíveis por 9.
42
222
408
408
512
800
42
222
408
666
512
666
800
824
900
1124
666
900
1260
1737
824
900
1124
1260
1344
1600
1344
1824
1260
1344
1600
1824
2000
1824
1946
2000
b) Divisíveis por 3.
d) Divisíveis por 5.
f) Divisíveis por 8.
900
1260
h) Divisíveis por 10.
42
105
222
105
705
800
408
512
800
800
900
408
666
777
900
1005
1260
824
1344
1600
1600
2000
900
1005
1260
1455
1600
2000
1824
2000
1344
1455
1737
1260
1824
Exercício 02) (1,0) Responda as questões abaixo, justificando sua resposta através dos
critérios de divisibilidade já estudados.
a) 126 é múltiplo de 9?
d) 287 é múltiplo de 2?
g) 90 é múltiplo de 5?
Sim, pois 1 + 2 + 6 = 9, que
é múltiplo de 9
Não, pois não termina
em número par.
Sim, pois termina em zero.
b) 465 é múltiplo de 5?
e) 1 350 é múltiplo de 6?
h) 73 é múltiplo de 3?
Sim, pois termina em cinco.
Sim, pois é múltiplo de
2 e de 3.
Não, pois 7 + 3 = 10, que
não é múltiplo de 3.
c) 116 é múltiplo de 4?
f) 551 é múltiplo de 5?
i) 320 é múltiplo de 10?
Sim, pois os dois últimos
algarismos formam um
múltiplo de 4.
Não, pois não termina
em zero ou em cinco.
Sim, pois termina em zero.
Exercício 03) (1,0) Considere o número 847A, onde A representa um algarismo de 0 a 9.
Qual dos algarismos abaixo deverá ser o MAIOR valor de A, para que o número seja
divisível por 3? (Justifique sua resposta)
a) 2
b) 8
c) 5
d) 9
e) 0
Como 8 + 4 + 7 = 19, então para completar um número múltiplo de 3 A pode ser os
algarismos 2, 5 ou 8, logo o maior valor de A é 8 (alternativa b).
Exercício 04) (1,0) Considere o número 50B, onde B representa um algarismo de 0 a 9.
Qual dos algarismos abaixo deverá ser o MENOR valor de B, para que o número seja
divisível por 6?
a) 4
b) 8
c) 1
d) 7
e) 3
Como 5 + 0 = 5, então para completar um número múltiplo de 3 B pode ser os algarismos1,
4 ou 7. Porém para ser múltiplo de 2 B deve ser um algarismo par, logo B só pode ser 4
(alternativa a).
Exercício 05) (1,0) Qual é o menor número que devemos subtrair de 61577 para que a
diferença seja divisível ao mesmo tempo por 5 e por 9?
Soma dos algarismos: 6 + 1 + 5 + 7 + 7 = 26
Soma mais próxima divisível por 9: 18 (para isso deve-se subtrair 8 do número original, o
que não resultaria em um numero divisível por cinco)
Próxima soma: 9 (para isso deve-se subtrair 17, o que resulta em 61560, divisível por 5).
Logo o menor número que deverá ser subtraído do número original é 17.
Exercício 06) (1,0) Sendo x e y algarismos do número 32x84y, qual deve ser o menor valor
atribuído a cada uma dessas letras, tal que 32x84y seja divisível, simultaneamente, por 3 e
por 5?
Para ser divisível por 5 o número 32x84y deve terminar em 0 ou 5, logo Y = 0 ou Y = 5.
Para ser divisível por 3 a soma dos algarismos deve ser múltiplo de 3, sem considerar as
letras X e Y, temos 3 + 2 + 8 + 4 = 17 que não á múltiplo de 3. Se Y for zero então X = 1,
porém se Y for 5 X deverá ser 2, logo o menor valor atribuído a essas letras é X = 1 e Y = 0.
Exercício 07) (0,5) Qual é a soma dos 20 primeiros pares positivos?
a) 800
b) 420
c) 400
Sequência = 2 + 4 + 6 + .... + 40
Soma das extremidades = 2 + 40 = 42
Total de pares = 10
Soma total = 10 * 42 = 420 (alternativa b)
d) 200
e) 100
Exercício 08) (0,5) Qual é a soma dos 20 primeiros múltiplos positivos de 7?
a) 7007
b) 7000
c) 1470
d) 1407
e) 140
Sequência = 7 + 14 + ... + 140
Soma das extremidades = 7 + 140 = 147
Total de pares = 10
Soma total = 10 * 147 = 1470 (alternativa c)
Exercício 09) (0,5) (PUC-RIO 2008) A soma de todos os números naturais ímpares de 3
algarismos é:
a) 220000
b) 247500
c) 277500
d) 450000
e) 495000
Sequência: 101 + 103 + ... + 999
Soma das extremidades = 101 + 999 = 1100
Números ímpares da sequência = (1000 – 101 + 1) : 2 = 450 números ímpares
Números de pares = 450 : 2 = 225
Soma total = 225 * 1100 = 247 500 (alternativa b)
Exercício 10) (0,5) Em janeiro de certo ano, João estava ganhando R$ 700,00 por mês. Seu
patrão prometeu aumentar seu salário em R$ 40,00 todos os meses. Quanto João estará
ganhando em dezembro do ano seguinte?
Sequência: 700 + 740 + ...
Se forem 24 meses, então o último salário será 23 * 40 + 700 = 1 620.
Resposta: Logo João estará ganhando 1620 reais.
Exercício 11) (0,5) Um pai resolve depositar todos os meses certa quantia na caderneta de
poupança de sua filha. Pretende começar com R$ 5,00 e aumentar R$ 5,00 por mês, ou seja,
depositar R$ 10,00 no segundo mês, R$ 15,00 no terceiro mês e assim por diante. Após efetuar
o décimo quinto depósito, qual a quantia total depositada por ele?
Sequência = 5 + 10 + 15 + ... + 75
Soma das extremidades = 80
Número de pares = 15 : 2 = 7,5
Soma total = 7,5 * 80 = 600
Resposta: Terá depositado R$ 600,00.
Exercício 12) (0,5) Num programa de condicionamento físico uma pessoa começa correndo
300 metros num dia, 400 metros no dia seguinte, 500 metros no próximo dia e assim por diante até o
décimo dia. Qual o total de metros percorridos por essa pessoa nos 10 dias?
Sequência = 300 + 400 + 500 + ... +1200
Soma das extremidades = 300 + 1200 = 1 500 m
Número de pares = 10 : 2 = 5
Soma total = 5 * 1 500 = 7 500
Resposta: Terá percorrido 7 500 metros.
Exercício 13) (0,5) Ao financiar uma casa no total de 20 anos, Carlos fechou o seguinte
contrato com a financeira: para cada ano, o valor das 12 prestações deve ser igual e o valor
da prestação mensal em um determinado ano é R$ 50,00 a mais que o valor pago,
mensalmente, no ano anterior. Considerando que o valor da prestação no primeiro ano é de
R$ 150,00, determine o total pago pela casa.
1° ano: 12 * 150
2° ano: 12 * 200
...
20° ano: 12 * (150 + 19 * 50) = 12 * 1100
Soma: 150 + 200 + ... + 1 100
Soma das extremidades = 150 + 1 100 = 1 250
Número de pares = 20 : 2 = 10
Soma total = 10 * 1 250 = 12 500
Preço pago pela casa = 12 * 12 500 = R$ 150 000,00.
Exercício 14) (0,5) Wilson vestia-se para ir a uma festa. Separou as melhores roupas: duas
calças (uma branca e outra preta) e três camisetas (uma estampada, uma branca e uma
preta). E ai ficou em dúvida, sem saber com que roupa ir à festa. Antes de decidir, imaginou
todas as possibilidades de combinar uma calça e uma camiseta.
a) Faça, no papel, uma tabela com todas essas possibilidades.
Camiseta estampada
Camiseta branca
Camiseta preta
(Ce)
(Cb)
(Cp)
Calça branca (Çb)
Çb Ce
Çb Cb
Çb Cp
Calça preta (Çp)
Çp Ce
Çp Cb
Çp Cp
b) Determine por meio de uma multiplicação quantas são essas possibilidades.
São 3.2 = 6 possibilidades.
c) Mostre todas essas possibilidades usando a árvore de possibilidades.
Camiseta estampada
Calça branca
Camiseta branca
Camiseta preta
Camiseta estampada
Calça preta
Camiseta branca
Camiseta preta
Exercício 15) (0,5) Temos dois tipos de calça; dois tipos de blusa; e dois pares de sapato.
Quantas são as possibilidades de combinar uma blusa, uma calça e um par de sapatos?
São 2 * 2 * 2 = 8 possibilidades.