MATEMÁTICA
Graduação
Geometria Analítica
Silvio Antonio Bueno Salgado
Jander Pereira dos Santos
Silvio Antonio Bueno Salgado
Jander Pereira dos Santos
Geometria Analítica
MEC / SEED / UAB
2011
S164g Salgado, Silvio Antonio Bueno
Geometria analítica / Silvio Antonio Bueno Salgado, Jander Pereira dos Santos.
— São João del-Rei, MG : UFSJ, 2011.
165p.
Graduação em Matemática.
1. Geometria analítica. 2. Matemática I.Santos, Jander Pereira. II. Título.
Reitor
Helvécio Luiz Reis
Coordenador UAB/NEAD/UFSJ
Heitor Antônio Gonçalves
Comissão Editorial:
Fábio Alexandre de Matos
Flávia Cristina Figueiredo Coura
Geraldo Tibúrcio de Almeida e Silva
José do Carmo Toledo
José Luiz de Oliveira
Leonardo Cristian Rocha (Presidente)
Maria Amélia Cesari Quaglia
Maria do Carmo Santos Neta
Maria Jaqueline de Grammont Machado de Araújo
Maria Rita Rocha do Carmo
Marise Maria Santana da Rocha
Rosângela Branca do Carmo
Rosângela Maria de Almeida Camarano Leal
Terezinha Lombello Ferreira
Edição
Núcleo de Educação a Distância
Comissão Editorial - NEAD-UFSJ
Capa/Diagramação
Eduardo Henrique de Oliveira Gaio
CDU: 514.12
SUMÁRIO
Pra começo de conversa... - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 7
1 Introdução aos Vetores - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 9
1.1 Conceitos Básicos- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 11
1.2 O Conceito de Vetor- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 13
1.3 Operações com Vetores - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 16
1.3.1 Adição de vetores- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 16
1.3.3 Multiplicação por Escalar- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 18
1.3.2 Diferença de Vetores- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 17
2 Vetores: Um Tratamento Algébrico - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 21
2.1 Vetores no Plano - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -23
2.3 Vetores no Espaço - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 30
2.2 Operações com Vetores - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 25
3 Produtos de Vetores - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 35
3.1 Produto Escalar - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 37
3.3 Produto Vetorial - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 42
3.2 Ângulo entre Vetores- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 38
3.4 Produto Misto - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 46
4 Retas no Plano e no Espaço - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 49
4.1 Algumas Formas de Escrever a Equação de uma Reta - - - - - - - - - - - - - - - - - - 51
4.2 Posições Relativas de Retas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 57
4.3 Ângulos entre Retas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 60
4.4 Distância de Ponto a Reta - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 64
5 Planos - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 69
5.1 Equação de um Plano - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 71
5.3 Posições Relativas de Planos - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 79
5.2 Posições relativas de reta e plano - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 76
5.4 Ângulo entre Reta e Plano - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 83
5.5 Ângulo entre Dois Planos - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 84
5.6 Distância de Ponto a Plano - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 86
6 Mudança de Coordenadas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 91
6.1 Coordenadas Polares - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 93
6.3 Coordenadas Esféricas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 97
6.2 Coordenadas Cilíndricas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 95
6.4 Rotação e Translação - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 99
6.4.1 Rotação dos Eixos Coordenados - - - - - - - - - - - - - - - - - - - - - - - - - - - 104
6.4.2 Translação dos Eixos Coordenados - - - - - - - - - - - - - - - - - - - - - - - - - - 106
7 Cônicas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 109
7.1 Introdução - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 111
7.2 Elipse - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 113
7.2.1 Equação da Elipse com Centro na Origem do Sistema - - - - - - - - - - - - 106
7.2.2 Equação da Elipse com Centro no Ponto O′(x0, y0) - - - - - - - - - - - - - - - - 120
7.3 Hipérbole - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 126
7.3.1 Equação da Hipérbole com Centro na Origem - - - - - - - - - - - - - - - - - - 128
7.3.2 Equação da Hipérbole com Centro no Ponto O′(x0, y0) - - - - - - - - - - - - - 132
7.4 Parábola - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 137
7.4.1 Equação da Parábola com Vértice na Origem - - - - - - - - - - - - - - - - - - 138
7.4.2 Parábola com Vértice no Ponto V (x0, y0) - - - - - - - - - - - - - - - - - - - - - - - 142
8 Superfícies Quádricas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 147
8.1 Introdução - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 149
8.3 Hiperboloide de uma Folha - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 152
8.2 Elipsoide - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 150
8.4 Hiperboloide de Duas Folhas - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 154
8.5 Paraboloide Elíptico - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 156
8.6 Paraboloide Hiperbólico - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 158
8.7 Superfície Cônica - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 159
8.8 Superfície Cilíndrica - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 161
Para Final de Conversa... - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 163
Referências - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 165
Para Começo de Conversa...
Prezado(a) Aluno(a):
É com muita satisfação que estamos iniciando o estudo da disciplina de Geometria
Analítica. Convido cada um de vocês para mergulharmos profundamente nesta disciplina.
Todos nós já estudamos de alguma forma a disciplina chamada Geometria Analítica no
ensino médio. Aqui, estudaremos a Geometria Analítica com tratamento vetorial. Estamos
falando de Geometria Analítica, mas, você saberia dizer o que significa essa expressão?
Como ela surgiu?
A geometria analítica, se baseia nos estudos da geometria através da utilização da álgebra.
Os estudos iniciais estão ligados ao matemático francês, René Descartes (1596 -1650),
criador do sistema de coordenadas cartesianas. Os estudos relacionados à Geometria
Analítica datam seu início no século XVII. Descartes, ao relacionar a Álgebra com a
Geometria, criou princípios matemáticos capazes de analisar por métodos geométricos as
propriedades do ponto, da reta e da circunferência, determinando distâncias entre eles,
localização e pontos de coordenadas.
De agora em diante, nosso principal objetivo será de aproveitar essa disciplina da melhor
forma possível, a fim de que você possa enriquecer seus conhecimentos, revisando alguns
conceitos e conhecendo outros. Para elaboração deste texto, as principais referências
utilizadas foram Winterle (2006) e Boulos (1997).
Os conteúdos que abordaremos, nesta disciplina, são distribuídos em oito capítulos (ou
unidades). O tempo que você terá para cursar essa disciplina será de sessenta dias e você
deverá se organizar para estudar os seguintes tópicos:
• Introdução aos Vetores
• Vetores: Um Tratamento Algébrico
• Produtos de Vetores
• Retas no Plano e no Espaço
• Planos
• Mudança de Coordenadas
• Cônicas
• Superfícies Quádricas
Importante! Procure se organizar e dedicar da melhor forma possível a esta disciplina.
Caso você tenha qualquer tipo de dificuldade, procure trocar ideias com o tutor presencial,
com o tutor a distância ou com o professor da disciplina.
Que cada um de vocês aproveitem o máximo esta disciplina. Bons estudos!
Os Autores.
capítulo
1
Introdução aos Vetores
Objetivo
• Construir vetores no plano usando as operações vetoriais.
9
1.1
Conceitos Básicos
Quando nós falamos em vetores, geralmente, o que nos vem em mente é uma seta. Mas
não podemos ter isso como definição. Tal seta nos transmite uma ideia de deslocamento
ou de translação. Basicamente, podemos imaginar um ponto se deslocando de A para
B. Essa é a idéia mais simples que um vetor nos transmite. Assim, o deslocamento é
retilíneo, nos dando ideia de direção associada a uma reta. A extremidade da seta nos dá
ideia de sentido e o comprimento da seta nos mostra, segundo uma unidade, a distância
entre os pontos A e B. Note que tal seta que estamos imaginando não é um vetor, mas
representa a idéia que um vetor ou uma grandeza vetorial encerra. Vamos iniciar nossa
conversa, para atingirmos a definição precisa de vetor.
Segundo WINTERLE (2006), uma reta r é orientada quando se fixa nela um sentido
de percurso, considerado positivo e indicado por uma seta, como mostra a figura abaixo.
O sentido oposto é negativo. Uma reta orientada é denominada eixo.
Um segmento orientado é determinado por um par ordenado de pontos; o primeiro
chamado origem do segmento, o segundo chamado extremidade.
O segmento orientado de origem A e extremidade B será representado por AB e, geometricamente, indicado por uma seta que caracteriza visualmente o sentido do segmento.
Um segmento nulo é aquele cuja extremidade coincide com a origem.
11
Se AB é um segmento orientado, o segmento orientado BA é oposto de AB.
Fixada uma unidade de comprimento, a cada segmento orientado pode-se associar um
número real, não negativo, que é a medida do segmento em relação àquela unidade. A
medida do segmento orientado é o seu comprimento ou seu módulo. O comprimento do
segmento AB é indicado por AB.
Assim, o comprimento do segmento AB representado na figura anterior é de 5 unidades
de comprimento:
AB = 5 u.c
Agora, observe que:
• Os segmentos nulos têm comprimento igual a zero.
• AB = BA.
Dois segmentos orientados não nulos AB e CD têm a mesma direção se as retas
suportes desses segmentos são paralelas ou coincidentes.
Então, podemos enfatizar que:
• Só se pode comparar os sentidos de dois segmentos orientados se eles têm mesma
direção.
• Dois segmentos orientados opostos têm sentidos contrários.
12
Dois segmentos orientados, AB e CD, são equipolentes quando têm a mesma direção,
o mesmo sentido e o mesmo comprimento.
• Dois segmentos nulos são sempre equipolentes.
• A equipolência dos segmentos AB e CD é representada por AB ∼ CD.
Propriedades da Equipolência
1. AB ∼ AB (reflexiva).
2. Se AB ∼ CD, CD ∼ AB (simétrica).
3. Se AB ∼ CD, CD ∼ EF , AB ∼ EF (transitiva).
4. Dado um segmento orientado AB e um ponto C, existe um único ponto D tal que
AB ∼ CD.
1.2
O Conceito de Vetor
Definição 1.2.1. Vetor determinado por um segmento orientado AB é o conjunto de
todos os segmentos orientados equipolentes a AB.
13
→
−
Se indicarmos com −
v este conjunto, simbolicamente, poderemos escrever: →
v =
XY /XY ∼ AB, em que XY é um segmento qualquer do conjunto.
−→
→
O vetor determinado por AB é indicado por AB ou B − A ou −
v.
−→
Um mesmo vetor AB é determinado por uma infinidade de segmentos orientados,
chamados representantes desse vetor, e todos equipolentes entre si. Assim, um segmento
determina um conjunto que é o vetor, e qualquer um destes representantes determina
o mesmo vetor. Portanto, com origem em cada ponto do espaço, podemos visualizar
um representante de um vetor. Usando um pouco mais nossa capacidade de abstração,
se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos
caracterizando, através de representantes, a totalidade dos vetores do espaço. Ora, cada
um destes segmentos é um representante de um só vetor. Consequentemente, todos os
vetores se acham representados naquele conjunto que imaginamos.
→
As características de um vetor −
v são as mesmas de qualquer um de seus representantes,
isto é: o módulo, a direção e o sentido do vetor são o módulo, a direção e o sentido de
qualquer um de seus representantes.
→
→
O módulo de −
v é denotado por |−
v |.
−→ −−→
Dois vetores AB e CD são iguais, se, e somente se, AB ∼ CD.
Os segmentos nulos, por serem equipolentes entre si, determinam um único vetor,
−
→
chamado vetor nulo ou vetor zero, e que é denotado por O .
−→
−→
−→
−→
→
Dado um vetor −
v = AB, o vetor BA é o oposto de AB e se indica por −AB ou por
→
−−
v.
→
→
Um vetor −
v é unitário, se |−
v | = 1.
→
Definição 1.2.2. Versor de um vetor não nulo −
v é o vetor unitário de mesma direção e
−
mesmo sentido de →
v.
→
→
Os vetores −
u1 e −
u2 da figura são vetores unitários, pois ambos têm módulo 1. No
14
→
→
entanto, apenas −
u1 tem a mesma direção e o mesmo sentido de −
v . Portanto, este é o
→
versor de −
v.
→
−
Dois vetores −
u e→
v são colineares, se tiverem a mesma direção. Em outras palavras:
−
→
→
u e −
v são colineares se tiverem representantes AB e CD pertencentes a uma mesma
reta ou a retas paralelas.
→
→
→
Se os vetores não nulos −
u, −
v e −
w (o número de vetores não importa) possuem
representantes AB, CD e EF pertencentes a um mesmo plano π, diz-se que eles são
coplanares.
→
→
Guardemos bem o seguinte: dois vetores −
u e−
v quaisquer são sempre coplanares,
pois podemos sempre tomar um ponto no espaço e, com origem nele, imaginar os dois re-
15
→
→
presentantes de −
u e−
v pertencendo a um plano π que passa por este ponto.(WINTERLE,
2006).
1.3
Operações com Vetores
1.3.1
Adição de vetores
→
→
Sejam os vetores −
u e−
v representados pelos segmentos orientados AB e BC.
→
→
Os pontos A e C determinam um vetor −
s que é, por definição, a soma dos vetores −
u
→
→
→
→
e−
v , isto é, −
s =−
u +−
v.
Propriedades da adição
→
→
→
→
1. Comutativa: −
u +−
v =−
v +−
u.
→
→
→
→
→
→
2. Associativa: (−
u +−
v)+−
w =−
u + (−
v +−
w ).
−
→
−
→ −
→ →
→
→
3. Existe um só vetor nulo O tal que para todo o vetor −
v se tem: −
v + O = O +−
v =
−
→
v.
16
−
→
→
4. Qualquer que seja o vetor →
v , existe um só vetor −−
v (vetor oposto de −
v ) tal que
−
→
−
→
→
→
→
v + (−−
v ) = −−
v +−
v = O.
1.3.2
Diferença de Vetores
−
→ → −
→
→
Chama-se diferença de dois vetores −
u e−
v , e se representa por d = −
u −→
v , ao vetor
−
→
→
u + (−−
v ).
−
→
Dados dois vetores →
u e−
v , representados pelos segmentos orientados AB e AC, res→
→
→
pectivamente, e construído o paralelogramo ABCD , verifica-se que a soma −
s =−
u +−
v
→ → −
−
é representada pelo segmento orientado AD e que a diferença d = −
u −→
v é representada
pelo segmento orientado CB.
−
−
Exemplo 1.3.1. Dados dois vetores →
u e→
v não paralelos, construa, no mesmo gráfico,
→
→
→
→
−
→
→
→
os vetores −
u +−
v,−
u −−
v,→
v −−
u e −−
u −−
v , todos com origem em um mesmo ponto.
17
1.3.3
Multiplicação por Escalar
−
→
→
Dados um vetor −
v =
̸ 0 e um número real (ou escalar) k ̸= 0, chama-se produto do
−
→
→
número real k pelo vetor →
v o vetor −
p = k−
v , tal que:
→
→
→
a) módulo: |−
p | = |k −
v | = |k||−
v |;
→
b) direção: a mesma de −
v;
→
−
c) sentido: o mesmo de −
v , se k > 0, e contrário ao de →
v , se k < 0
−
→
→
Se k = 0 ou −
v = 0, o produto é o vetor O . Se k é um escalar não nulo, a notação
−
→
→
→
→
→
→
v /k significa 1/k −
v . Se −
v é um vetor não nulo, o vetor −
v /|−
v | é o versor de −
v.
Propriedades da Multiplicação por Escalar
→
→
Se −
u e−
v são vetores quaisquer, e a e b, números reais, temos:
18
→
→
1. Associativa: a(b−
v ) = (ab)−
v.
→
→
→
2. Distributiva em relação à adição de escalares: (a + b)−
v = a−
v + b−
v.
→
→
→
→
3. Distributiva em relação à adição de vetores: a(−
u +−
v ) = a−
u + a−
v.
→
→
4. Identidade: 1−
v =−
v.
→
→
Dois vetores não nulos −
u e−
v são paralelos, se, e somente se, existe um escalar k tal
−
→
→
→
que →
u = k−
v (e, consequentemente, k ̸= 0 e −
v =−
u /k).
Atividade
→
→
1. Dados dois vetores −
u e−
v não paralelos, construa em uma mesma figura os vetores
→
→
→
→
→
→
2−
u + 3−
v , 3−
u − 2−
v , −−
v −−
u e todos com origem em um mesmo ponto.
19
capítulo
2
Vetores:
Um Tratamento Algébrico
Objetivos
• Estabelecer a igualdade entre dois vetores;
• Manipular operações entre vetores;
• Reconhecer vetores paralelos;
• Representar vetores no espaço.
21
2.1
Vetores no Plano
→
→
Segundo WINTERLE (2006), dados dois vetores −
v1 e −
v2 , não colineares, qualquer vetor
−
→
−
→
→
−
v (coplanar com →
v1 e −
v2 ) pode ser decomposto segundo as direções de −
v1 e →
v2 e cuja
→
soma seja −
v . Em outras palavras, iremos determinar dois números reais a1 e a2 tais que:
−
→
→
→
v = a1 −
v1 + a2 −
v2
(2.1)
→
→
Quando o vetor −
v estiver representado por 2.1 dizemos que −
v é combinação linear
→
→
→
→
de −
v1 e −
v2 . O par de vetores −
v1 e −
v2 , não colineares, é chamado base do plano. Aliás,
→
→
qualquer conjunto {−
v1 , −
v2 } de vetores não colineares constitui uma base no plano. Os
→
números a1 e a2 da representação 2.1 são chamados componentes ou coordenadas de −
v
−
→
→
→
→
em relação à base {→
v1 , −
v2 }. O vetor a1 −
v1 é chamado projeção de −
v sobre −
v1 segundo a
−
→
→
−
direção de →
v2 . Do mesmo modo, a2 −
v2 é a projeção de −
v sobre →
v2 segundo a direção de
−
→
v1 .
Na prática, as bases mais utilizadas são as bases ortonormais.
→
→
Uma base {−
e1 , −
e2 } é dita ortonormal se os seus vetores forem ortogonais e unitários,
→
→
−
→
isto é, −
e1 ⊥ −
e2 e |→
e1 | = |−
e2 | = 1.
Dentre as infinitas bases ortonormais no plano, uma delas é particularmente importante. Trata-se da base que determina o conhecido sistema cartesiano ortogonal xOy. Os
23
→ →
−
−
vetores ortogonais e unitários, neste caso, são simbolizados por i e j , ambos com ori−
→ →
−
gem em O e extremidades em (1, 0) e (0, 1), respectivamente, sendo a base C = { i , j }
→
−
→
−
chamada canônica. Portanto, i = (1, 0) e j = (0, 1).
Daqui por diante, trataremos somente da base canônica.
→
Dado um vetor −
v qualquer do plano , existe uma só dupla de números x e y tal que
−
→
−
→
−
→
v =x i +y j
(2.2)
→
Os números x e y são as componentes de −
v na base canônica. A primeira componente
→
→
é chamada abscissa de −
v e a segunda componente y é a ordenada de −
v.
−
O vetor →
v será também representado por
−
→
v = (x, y)
dispensando-se a referência à base canônica C.
24
(2.3)
→
A igualdade anterior é chamado expressão analítica de −
v . Para exemplificar, veja
alguns vetores e suas correspondentes expressões analíticas:
−
→
−
→
−
→
−
→
3 i − 5 j = (3, −5)
3 j = (0, 3)
− 4 i = (−4, 0)
Parece óbvio o que se segue, mas a definição de igualdade de vetores é fundamental
para continuarmos o estudo de Geometria Analítica.(WINTERLE,2006).
→
→
Dois vetores −
u = (x1 , y1 ) e −
v = (x2 , y2 ) são iguais se, e somente se, x1 = x2 e y1 = y2 ,
−
→
escrevendo-se →
u =−
v.
→
→
Exemplo 2.1.1. O vetor −
u = (x + 1, 4) é igual ao vetor −
v = (5, 2y − 6) se x + 1 = 5 e
→
→
→
→
2y − 6 = 4. Assim, se −
u =−
v , então x = 4, y = 5 e −
u =−
v = (5, 4).
Atividade
→
→
Considere os vetores −
u = (m + 2n, n − 7) e −
v = (4 − m, n + m + 9). Existem valores de
−
→
m e n de modo que →
u =−
v?
2.2
Operações com Vetores
Você deve ter notado que já estudamos operações entre vetores. Por que então, tudo
isso novamente? A questão é que estudamos operações entre vetores do ponto de vista
geométrico. Agora daremos um enfoque algébrico para o que fizemos anteriormente.
→
→
Sejam os vetores −
u = (x1 , y1 ) e −
v = (x2 , y2 ) e α ∈ ℜ. Define-se:
25
→
→
1. −
u +−
v = (x1 + x2 , y1 + y2 )
→
2. α−
u = (αx1 , αx2 )
Portanto, para somar dois vetores, somam-se as correspondentes coordenadas, e para
multiplicar um número real por um vetor, multiplica-se cada componente do vetor por
este número.
1→ −
→
→
→
Exemplo 2.2.1. Determinar o vetor −
w na igualdade 3−
w + 2−
u = −
v +→
w , sendo dados
2
→
−
→
u = (3, −1) e −
v = (−2, 4).
A equação pode ser resolvida como uma equação numérica:
→
→
→
→
→
→
→
→
6−
w + 4−
u =−
v + 2−
w
=⇒
6−
w − 2−
w =−
v − 4−
u
=⇒
1→ −
→
−
w = −
v −→
u
4
→
→
Substituindo −
u e−
v na equação acima, vem
1
1
→
−
→
w = (−2, 4) − (3, −1) =⇒ −
w = (− , 1) − (3, −1) =⇒
4
4
7
→
−
w = (− , 2)
2
→
→
→
4−
w =−
v − 4−
u
=⇒
1
−
→
w = (− + (−3), 1 + 1)
2
−→
Vamos considerar agora o vetor AB de origem no ponto A(x1 , y1 ) e extremidade em
B(x2 , y2 ).
26
=⇒
−→ −−→
−→
−−→
Os vetores OA e OB têm expressões analíticas OA = (x1 , y1 ) e OB = (x2 , y2 ). Por
−→ −→ −−→
−→ −−→ −→
outro lado, do triângulo OAB da figura, vem OA + AB = OB em que AB = OB − OA
−→
−→
−→
ou AB = (x2 , y2 ) − (x1 , y1 ) e AB = (x2 − x1 , y2 − y1 ) isto é, as componentes de AB são
obtidas subtraindo-se das coordenadas da extremidade B as coordenadas da origem A,
−→
razão pela qual também se escreve AB = B − A.
É importante lembrar que um vetor tem infinitos representantes que são os segmentos
orientados de mesmo comprimento, mesma direção e mesmo sentido. E, dentre os infinitos
−→
representantes do vetor AB, o que melhor o caracteriza é aquele que tem origem em O(0, 0)
e extremidade em P = (x2 − x1 , y2 − y1 ).
−→
−→
−
O vetor →
v = AB é também chamado vetor posição ou representante natural de AB.
−→
→
→
Por outro lado, sempre que tivermos −
v = AB ou −
v = B − A podemos também
−→
→
→
concluir que B = A + −
v ou B = A + AB, isto é, o vetor −
v “transporta” o ponto inicial
A para o ponto extremo B.
Exemplo 2.2.2. Dados os pontos A(−1, 2), B(3, −1) e C(−2, 4), determinar o ponto D
−−→ 1 −→
de modo que CD = AB.
2
−−→
−→
Seja D(x, y). Então, CD = D − C = (x, y) − (−2, 4) = (x + 2, y − 4) e AB = B − A =
27
(3, −1) − (−1, 2) = (4, −3). Logo,
1
(x + 2, y − 4) = (4, −3)
2
(x + 2, y − 4) = (2,
−3
)
2
Da igualdade anterior concluimos que
x+2 =
2
y − 4 = − 32
5
Portanto, D(0, ).
2
Para você Refletir: Pense outra forma de resolver este exercício.
Vimos anteriormente, como determinar o vetor definido por dois pontos. Considere
agora o segmento de extremos A(x1 , y1 ) e B(x2 , y2 ). Sendo M (x, y) o ponto médio de AB,
−−→ −−→
podemos expressar de forma vetorial como AM = M B ou
(x − x1 , y − y1 ) = (x2 − x, y2 − y)
e daí
x − x1 = x2 − x
e y − y1 = y2 − y).
Com isso , temos
M(
x1 + x2 y1 + y2
,
)
2
2
28
Exemplo 2.2.3. Observe que o ponto médio do segmento de extremos A(−2, 3) e B(6, 2)
é
M(
−2 + 6 3 + 2
,
)
2
2
ou
5
M (2, )
2
Você se lembra da definição de vetores paralelos? Pois bem, vamos voltar nesse assunto,
mas agora, com a abordagem algébrica.
→
→
Dois vetores são paralelos se existe um número real α tal que −
u = α−
v , ou seja,
(x1 , y1 ) = α(x2 , y2 ) que pela condição de igualdade resulta em x1 = αx2 e y1 = αy2 donde
x1
y1
= (= α)
x2
y2
Esta é a condição de paralelismo de dois vetores, isto é, dois vetores são paralelos
quando suas componentes forem proporcionais.
−2
3
−
−
Exemplo 2.2.4. Os vetores →
u = (−2, 3) e →
v = (−4, 6) são paralelos pois
= .
−4
6
Atividades
→
→
→
→
1. Dados os vetores −
u = (3, −1) e −
v = (−1, 2), obtenha o vetor −
w tal que 3−
w −
→
→
→
→
(2−
v −−
u ) = 2(4−
w − 3−
u ).
2. Dados os pontos A(−1, 3), B(1, 0) e C(2, −1), determine o ponto D de modo que
−−→ −→
DC = BA.
29
2.3
Vetores no Espaço
Vamos refletir um pouco sobre o que vimos até agora. Iniciamos nossa disciplina dando
aos vetores um tratamento geométrico. Em seguida, vimos que todo vetor de um plano
possui uma representação em termos da chamada base canônina. Ou seja , passamos a
manipular os vetores do ponto de vista algébrico. Uma questão fundamental, é que tudo
o que fizemos para vetores em um plano se estende de maneira natural para vetores do
espaço, bastanto para isso fazer algumas adptações.
→
→ −
−
→ −
No espaço, de forma análoga, consideraremos a base canônica { i , j , k } , onde estes
três vetores unitários e dois a dois ortogonais estão representados com origem no ponto
O. Este ponto e a direção de cada um dos vetores da base determinam os três eixos
−
→
cartesianos: o eixo Ox ou eixo dos x (das abscissas) corresponde ao vetor i , o eixo Oy
−
→
ou eixo dos y (das ordenadas) corresponde ao vetor j e o eixo Oz ou eixo dos z (das
−
→
cotas) corresponde ao vetor k . As setas nessa figura indicam o sentido positivo de cada
eixo, chamado também de eixo coordenado.
Cada dupla de vetores de base, e, consequentemente, cada dupla de eixos, determina
um plano coordenado. Portanto, temos três planos coordenados: o plano xOy ou xy, o
plano xOz ou xz e o plano yOz ou yz. As figuras a seguir dão uma idéia dos planos xy e
30
xz, respectivamente.
Assim como no plano, a cada ponto P (x, y, z) do espaço irá corresponder o vetor
−
→
−→
→
−
→
−
OP = x i + y j + z k , isto é, as próprias coordenadas x, y e z do ponto P são as
−→
componentes do vetor OP na base canônica. As coordenadas x, y e z são denominadas
−
→
−→ →
−
→
−
→
abscissa, ordenada e cota, respectivamente. O vetor OP = −
v = x i + y j + z k também
−→ →
será expresso por OP = −
v = (x, y, z).
Tomemos o paralelepípedo da figura:
Com base nesta figura, temos:
a) A(2, 0, 0) - um ponto P (x, y, z) está no eixo dos x, quando y = 0 e z = 0;
b) C(0, 4, 0) - um ponto está no eixo dos y, quando x = 0 e z = 0;
31
c) E(0, 0, 3) - um ponto está no eixo dos z, quando x = 0 e y = 0;
d) B(2, 4, 0) - um ponto está no eixo dos xy quando z = 0;
e) F (2, 0, 3) - um ponto está no eixo dos xz, quando y = 0;
f ) D(0, 4, 3) - um ponto está no eixo dos yz, quando x = 0.
O ponto B é a projeção de P no plano xy, assim D e F são as projeções de P nos
planos yz e xz, respectivamente. O ponto A(2, 0, 0) é a projeção de P (2, 4, 3) no eixo
dos x, assim como C(0, 4, 0) e E(0, 0, 3) são as projeções de P nos eixos dos y e dos z,
respectivamente.
Como todos os pontos da face
a) P DEF distam 3 unidades do plano xy e estão acima dele, são pontos de cota z = 3,
isto é, são pontos do tipo (x, y, 3);
b) P BCD distam 4 unidades do plano xz e estão à direita dele, são pontos de ordenada
y = 4, isto é, são pontos do tipo (x, 4, z);
c) P F AB distam 2 unidades do plano yz e estão à frente dele, são pontos de abscissa
x = 2, isto é, são pontos do tipo (2, y, z).
Ao desejarmos marcar um ponto no espaço, digamos A(3, −2, 4), procedemos assim:
′
1o ) Marca-se o ponto A (3, −2) no plano xy;
′
2o ) Desloca-se A paralelamente ao eixo dos z, 4 unidades para cima (se fosse −4 seriam
4 unidades para baixo) para obter o ponto A.
32
Atividades
1. Considere os seguintes pontos: A(4, 0, 1), B(5, 1, 3), C(3, 2, 5) e D(2, 1, 3). Represente cada um desses pontos no sistema cartesiano. Utilize o que aprendermos anteriormente, para demonstrar que esses pontos são vértices de um paralelogramo.(
Lembre da definição de paralelogramo!).
→
→
2. Obtenha os valores de a e b de modo que os vetores −
u = (4, 1, −3) e −
v = (6, a, b)
sejam paralelos.
33
capítulo
Produtos de Vetores
Objetivos
• Calcular a norma de um vetor a partir de sua expressão analítica;
• Calcular o ângulo formado entre dois vetores;
• Determinar o vetor projeção;
• Calcular o produto vetorial entre dois vetores;
• Utilizar o produto vetorial para calcular a área de um paralelogramo;
• Reconhecer vetores coplanares com o uso do produto misto.
35
3
3.1
Produto Escalar
→
Definição 3.1.1. Chama-se produto escalar ou produto interno de dois vetores −
u =
−
→ →
−
→
−
→
→
−
→
−
−
→
→
→
x1 i + y1 j + z1 k e −
v = x2 i + y2 j + z2 k , e se representa por −
u ·−
v , ao número real
−
→
→
u ·−
v = x 1 x 2 + y 1 y 2 + z1 z2 .
→
→
→
→
→
O produto escalar de −
u por −
v também é denotado por < −
u ,−
v > e se lê “ −
u escalar
−
→
v ”.
−
→ →
→
−
→
−
→
−
→
−
→ −
→
Exemplo 3.1.1. Dados os vetores −
u = 3 i −5j +8k e −
v = 4 i − 2 j − k , tem-se:
−
→
→
u ·−
v = 3(4) − 5(−2) + 8(−1) = 12 − 10 − 8 = 14
.
→
−
Definição 3.1.2. Módulo ou norma de um vetor −
v ,denotado por | →
v | é o número real
não negativo
→
|−
v |=
√
−
→
→
v .−
v
→
Caso −
v = (x, y), teremos
−
|→
v |=
√
(x, y).(x, y)
ou ainda
→
|−
v |=
√
x2 + y 2
→
−
Apartir de cada vetor −
v não nulo é possível obter um vetor unitário →
u fazendo
37
−
→
v
−
→
u = −
→
| v |
Vamos agora explorarmos algumas propriedades básicas do produto escalar.
→
→
→
Para quaisquer vetores −
u, −
v e−
w e o número real α, é fácil verificar que:
→
→
→
→
1. −
u ·−
v =−
v ·−
u
→
→
→
→
→
→
→
→
→
→
→
→
→
→
2. −
u · (−
v +−
w) = −
u ·−
v +−
u ·−
w e (−
u +−
v)·−
w =−
u ·−
w +−
v ·−
w
→
→
→
→
→
→
3. α(−
u ·−
v ) = (α−
u)·−
v =−
u · (α−
v)
→ − −
−
−
→
→
→
−
→
4. −
u ·−
u > 0 se →
u =
̸ 0 e→
u ·→
u = 0, se −
u = 0 = (0, 0, 0)
→
→
→
5. −
u ·−
u = |−
u |2
3.2
Ângulo entre Vetores
→
→
Definição 3.2.1. O ângulo de dois vetores não nulos −
u e−
v é o ângulo θ formado pelas
semiretas OA e OB e tal que 0 ≤ θ ≤ π.
A ideia, agora, é estabelecermos uma maneira de calcular o ângulo formado entre dois
vetores, a partir de suas componentes. Aplicando a lei dos cossenos ao triângulo ABC da
38
figura abaixo, temos
→
→
→
→
→
→
|−
u −−
v |2 = |−
u |2 + |−
v |2 − 2|−
u ||−
v |cos θ
(3.1)
Por outro lado, tem-se:
→
→
→
→
→
→
|−
u −−
v |2 = |−
u |2 + |−
v |2 − 2−
u−
v
(3.2)
→
→
→
→
→
→
Comparando as igualdades 3.1 e 3.2 resulta em: |−
u |2 + |−
v |2 − 2−
u−
v = |−
u |2 + |−
v |2 −
→
→
2|−
u ||−
v |cosθ e daí,
−
→
→
→
→
u ·−
v = |−
u ||−
v |cos θ,
(3.3)
para 0o ≤ θ ≤ 180o .
Conclusão: O produto escalar de dois vetores não nulos é igual ao produto de seus
módulos pelo cosseno do ângulo por eles formado.
→
→
Exemplo 3.2.1. Calcule o ângulo entre os vetores −
u = (1, 1, 4) e −
v = (−1, 2, 2).
√
√
−
→
−
→
−1 + 2 + 8
u · v
(1, 1, 4) · (−1, 2, 2)
9
1
1 2
2
√
= √ √
cos θ = −
=√
= √
=√ =√ √ =
→
−
→
2
| u || v √
|
1 + 1 + 16 1 + 4 + 4
18 9
3 2·3
2
2 2
2
concluimos que θ = π4 radianos.
Como cos θ =
2
→
→
Agora, vamos questionar o seguinte fato: O que ocorre com a relação 3.3 caso −
u ·−
v =
0? Podemos verificar que neste caso cos θ deve ser igual a zero, isto é, cos θ = 0, o que
implica θ = 90o , ou seja, θ é ângulo reto.
39
Assim, podemos afirmar que dois vetores são ortogonais se, e somente se, o produto
escalar deles é nulo, isto é, se:
−
→
→
u ·−
v =0
→
→
→
→
e esses vetores serão denotados por −
u ⊥−
v (lê-se vetor −
u ortogonal ao vetor −
v ).
−
→
Exemplo 3.2.2. Verifique que →
u = (−2, 3 − 2) é ortogonal a −
v = (−1, 2, 4).
−
→
→
u ·−
v = −2(−1) + 3(2) + (−2)4 = 2 + 6 − 8 = 0
→
→
Portanto −
u ⊥−
v.
Vamos discutir agora a questão da projeção vetorial. Mas o que vem a ser isso?
→
→
Considere os vetores −
u e−
v não nulos e θ o ângulo entre eles. Pretendemos decompor
−
→
→
→
→
→
→
→
um dos vetores, digamos →
v , tal que −
v =−
v1+−
v 2 sendo −
v 1 //−
u e−
v2⊥−
u.
A figura a seguir ilustra as duas situações possíveis, podendo ser θ um ângulo agudo
ou obtuso.
−
→
→
O vetor →
v 1 é chamado projeção ortogonal de −
v sobre −
u e denotado por
−
→
−
→
→
v 1 = proj−
u v .
40
(3.4)
→
→
→
→
−
→
→
→
→
Ora, sendo −
v 1 //−
u , temos −
v 1 = α−
u e como →
v2=−
v −−
v1 = −
v − α−
u é ortogonal a
−
→
u , vem
→
→
→
(−
v − α−
u)·−
u =0
ou
−
→
→
→
→
v ·−
u − α−
u ·−
u =0
−
→
→
v ·−
u
→
→
eα= −
. Portanto, sendo −
v 1 = α−
u , por 3.4 conclui-se que
→
−
→
u · u
−
→
→
v ·−
u −
→
−
→
proj−
v
=
(
)→
u
u
−
→
−
→
u · u
(3.5)
→
→
Exemplo 3.2.3. Determine o vetor projeção de −
u = (2, 3, 4) sobre −
v = (1, −1, 0).
→
−
→
−
u · v −
(2, 3, 4) · (1, −1, 0)
2−3+0
1
−
→
→
proj−
)→
v =(
)(1, −1, 0) = (
)(1, −1, 0) = − (1, −1, 0)
v u = (−
→
→
−
(1, −1, 0) · (1, −1, 0)
1+1+0
2
v · v
Atividades
→
→
→
→
→
→
1. Mostre que | −
u +−
u |=| −
u |2 +2−
u−
v+|−
u |2 .
→
2. Determine o valor de n para que o vetor −
u = (n, 25 , 54 ) seja unitário.
3. Calcule o perímetro do triângulo de vértices A(0, 1, 2), B(−1, 0, −1) e C(2, −1, 0).
4. Determine os ângulos do triângulo de vértices A(2, 1, 3), B(1, 0, −1) e C(−1, 2, 1).
→
→
5. Determine o vetor projeção do vetor −
u (1, 2, −3) na direção de −
v = (2, 1, −2).
41
3.3
Produto Vetorial
Faremos algumas considerações importantes antes de definirmos produto vetorial:
→
→
• O produto vetorial é um vetor, ao contrário do produto escalar −
u ·−
v que é um
escalar (número real);
• Para simplicidade do cálculo do produto vetorial, faremos uso de determinantes;
• Algumas propriedades dos determinantes serão utilizadas nesta seção:
a) a permutação de duas linhas de uma matriz inverte o sinal do determinante
associado a essa matriz;
b) se duas linhas de uma matriz forem constituídas de elementos proporcionais, seu
determinante é igual a zero(duas linhas iguais é um caso particular).
c) se uma das linhas de uma matriz for constituída de zeros, o determinante é igual
a zero.
• O determinante associado a uma matriz de ordem 3 pode ser dado por
a b c
x1 y 1
x 1 z1
y 1 z1
det
c
b + det
a − det
x1 y1 z1 = det
x2 y 2
x 2 z2
y 2 z2
x 2 y 2 z2
A expressão da direita é conhecida como desenvolvimento do determinante pelo Teorema de Laplace aplicado à primeira linha.
42
−
→
−
→
−
→
→
Definição 3.3.1. Chama-se produto vetorial de dois vetores −
u = x 1 i + y 1 j + z1 k
−
→
−
→
−
→
→
→
→
e−
v = x2 i + y2 j + z2 k , tomados nesta ordem, e se representa por −
u ×−
v , ao vetor
→
→
→
y 1 z1 −
x 1 z1 −
x1 y1 −
−
→
→
u ×−
v = det
(3.6)
i − det
j + det
k
y 2 z2
x 2 z2
x2 y2
−
−
→
→
→
O produto vetorial de →
u por →
v também é denotado por −
u ∧−
v e lê-se “ −
u vetorial
−
→
v ”.
→
→
Observemos que a definição de −
u ×−
v dada em 3.6 pode ser obtida do desenvolvimento
segundo o Teorema de Laplace (item d acima) substituindo-se a, b e c pelo vetores unitários
→
→ −
−
→ −
i , j e k , fato que sugere a notação
→
−
→ −
→ −
i j k
−
→
→
u ×−
v = det
(3.7)
x
y
z
1
1
1
x2 y2 z2
Atenção: O símbolo à direita de 3.7 não é um determinante, pois a primeira
linha contém vetores em vez de escalares. No entanto, usaremos esta notação
pela facilidade de memorização que ela propicia no cálculo do produto vetorial.
Exemplo 3.3.1.
−
→ −
→
i j
det
5 4
1 0
−
→ → −
→
−
→
−
→
→ −
→
→
→
Calcular −
u ×−
v para −
u =5 i +4j +3k e −
v = i + k.
−
→
k
→
→
→
5 4 −
5 3 −
4 3 −
j
+
det
i
−
det
=
det
k
3
1 0
1 1
0 1
1
−
→
−
→
−
→
−
→
−
→
−
→
= (4 − 0) i − (5 − 3) j + (0 − 4) k = 4 i − 2 j − 4 k
Agora, conforme fizemos com o produto escalar, vamos discutir algumas propriedades
do produto vetorial.
43
Levando-se em conta as considerações feitas sobre as propriedades dos determinantes,
concluímos de imediato que:
→
→
→
→
→
→
→
→
1. −
v ×−
u = −(−
u ×−
v ), isto é, os vetores −
v ×−
u e−
u ×−
v são opostos , pois a troca
−
→
de ordem dos vetores no produto vetorial →
u ×−
v implica troca de sinal de todos os
determinantes de ordem 2, ou seja, troca de sinal de todas as suas componentes.
−
→
→
→
→
→
2. −
u ×−
v = 0 se, e somente se, −
u //−
v , pois neste caso, todos os determinantes de
ordem 2 têm suas linhas constituídas por elementos proporcionais.
Estão aí também incluídos os casos particulares:
−
→
→
→
I) −
u ×−
u = 0 (determinantes de ordem 2 com linhas iguais)
−
→ −
→
→
II) −
u × 0 = 0 (determinantes de ordem 2 com uma linha de zeros)
→
→
Características do vetor −
u ×−
v
→
→
Consideremos os vetores −
u = (x1 , y1 , z1 ) e −
v = (x2 , y2 , z2 )
→
→
a) Direção de −
u ×−
v
→
→
→
→
O vetor −
u ×−
v é simultaneamente ortogonal a −
u e−
v.
→
→
b) Sentido de −
u ×−
v
→
→
O sentido de −
u ×−
v poderá ser determinado utilizando-se a “regra da mão direita”.
→
→
→
Sendo θ o ângulo entre −
u e−
v , suponhamos que −
u (1o vetor) sofra uma rotação de
→
ângulo θ até coincidir com −
v . Se os dedos da mão direita forem dobrados na mesma
→
→
direção da rotação, então o polegar estendido indicará o sentido de −
u ×−
v.
A figura acima (b) mostra que o produto vetorial muda de sentido quando a ordem
dos vetores é invertida. Observemos que só será possível dobrar os dedos na direção
→
→
de −
v para −
u se invertermos a posição da mão, quando então o dedo polegar estará
apontando para baixo.
44
→
→
c) Comprimento de −
u ×−
v
→
→
→
→
→
→
Se θ é o ângulo entre os vetores −
u e−
v não-nulos, então |−
u ×−
v | = |−
u ||−
v |sen θ.
→
→
Proposição 3.3.1. O módulo do produto vetorial dos vetores −
u e −
v mede a área do
−→ → −→
→
paralelogramo ABCD determinado pelos vetores −
u = AB e −
v = AC
Demonstração. De fato a área
→
→
→
→
→
ABCD =| −
u | h =| −
u || −
v | sin θ =| −
u || −
v | sin θ
Usando o fato que
→
→
→
→
|−
u ×−
v |=| −
u || −
v | sin θ
segue o resultado.
Atividades
→
→
→
1. Considere os vetores −
u = (2, −1, 1), −
v = (1, −1, 0) e −
w = (−1, 2, 2). Calcule:
−
→
→
−
→
→
v ×−
w , (→
v +−
u)×−
w.
→
→
2. Calcule a área do paralelogramo definido pelos vetores −
u = (3, 1, 2) e −
v = (4, −1, 0).
45
3.4
Produto Misto
−
→ →
→
−
−
→
→
Definição 3.4.1. Chama-se produto misto dos vetores −
u = x 1 i + y 1 j + z1 k , −
v =
−
→ →
→
−
−
→
−
→
−
→
−
→
x 2 i + y 2 j + z2 k e −
w = x3 i + y3 j + z3 k , tomados nesta ordem, ao número real
−
→
→
→
u · (−
v ×−
w ).
→
→
→
→
→
→
O produto misto de −
u, −
v e−
w também pode ser denotado por (−
u ,−
v ,−
w ).
Tendo em vista
−
→
i
→
−
→
v ×−
w = det
x2
x3
vem
que
→
−
→ −
j k
→
→
→
x 2 y2 −
x 2 z2 −
y 2 z2 −
j
+det
i
−det
=
det
k
y 2 z2
x 3 y3
x 3 z3
y 3 z3
y 3 z3
y 1 z1
x 1 z1
x1 y1
−
→
→
→
u · (−
v ×−
w ) = x1 det
− y1 det
+ z1 det
y 2 z2
x 2 z2
x2 y2
e, portanto,
x 1 y 1 z1
−
→
→
→
u · (−
v ×−
w ) = det
x
y
z
2 2 2
x 3 y 3 z3
(3.8)
−
→ −
−
→
−
→
→
Exemplo 3.4.1. Calcular o produto misto dos vetores −
u = 2 i + 3j + 5k, →
v =
−
→ →
−
→
−
→
−
→
−
→
−
→
− i +3j +3k e −
w =4 i −3j +2k.
3 5
2
−
→
→
→
u · (−
v ×−
w ) = det
−1 3 3 = 27
4 −3 2
46
Vejamos agora algumas propriedades do produto misto.
−
→
→
1. O produto misto (→
u ,−
v ,−
w ) muda de sinal ao trocarmos a posição de dois vetores.
→
→
→
Então, se em relação ao produto misto (−
u ,−
v ,−
w ) ocorrer
a) uma permutação - haverá troca de sinal;
b) duas permutações - não altera o valor.
−
Resulta desta propriedade que os sinais · e × podem ser permutados, isto é, →
u ·
→
→
→
→
→
(−
v ×−
w ) = (−
u ×−
v)·−
w.
→
→
→
→
→
→
→
→
→
→
2. (−
u +−
x ,−
v ,−
w ) = (−
u ,−
v ,−
w ) + (−
x ,−
v ,−
w)
→
→
→
→
→
→
→
→
→
→
(−
u ,−
v +−
x ,−
w ) = (−
u ,−
v ,−
w ) + (−
u ,−
x ,−
w)
→
→
→
→
→
→
→
→
→
→
(−
u ,−
v ,−
w +−
x ) = (−
u ,−
v ,−
w ) + (−
u ,−
v ,−
x)
→
→
→
→
→
→
→
→
→
→
→
→
3. (α−
u ,−
v ,−
w ) = (−
u , α−
v ,−
w ) = (−
u ,−
v , α−
w ) = α(−
u ,−
v ,−
w)
→
→
→
4. (−
u ,−
v ,−
w ) = 0 se, e somente se, os três vetores forem coplanares.
−
−
Exemplo 3.4.2. Verificar se são coplanares os vetores →
u = (2, −1, 1), →
v = (1, 0, −1) e
−
→
w = (2, −1, 4).
2 −1 1
→
→
→
= 3 ̸= 0
(−
u ,−
v ,−
w ) = det
1
0
−1
2 −1 4
Portanto, os vetores não são coplanares.
47
→
→
Exemplo 3.4.3. Qual deve ser o valor de m para que os vetores −
u = (2, m, 0), −
v =
→
(1, −1, 2) e −
w = (−1, 3, −1) sejam coplanares?
2 m 0
→
→
→
Devemos ter (−
u ,−
v ,−
w ) = 0, isto é, det
1 −1 2
−1 3 −1
e, portanto, m = −10.
= 0 ou 2−2m−12+m = 0
Exemplo 3.4.4. Verifique se os pontos A(1, 2, 4), B(−1, 0, −2), C(0, 2, 2) e D(−2, 1, −3)
estão no mesmo plano.
−→ −→ −−→
Os quatro pontos dados são coplanares se forem coplanares os vetores AB, AC e AD,
−→ −→ −−→
e para tanto, deve-se ter (AB, AC, AD) = 0. Como
−2 −2 −6
−→ −→ −−→
(AB, AC, AD) =
−1 0 −2 = 0
−3 −1 −7
Portanto os pontos A, B, C e D são coplanares.
Atividades
→
→
→
1. Verifique se os vetores −
u = (3, 1, −2), −
v = (1, 2, 1) e −
w = (−2, 3, 4) são coplanares.
2. Para que valores de a os pontos A(a, 1, 2), B(2, −2, 3), C(5, −1, 1) e D(3, −2, 2) são
coplanares?
48
capítulo
4
Retas no Plano e no Espaço
Objetivos
• Identificar as diferentes formas de escrever a equação de uma reta;
• Calcular o ângulo formado por duas retas;
• Reconhecer a posição relativa de duas retas;
• Calcular a distância de um ponto a uma reta.
49
4.1
Algumas Formas de Escrever a Equação de uma
Reta
→
Consideremos um ponto A(x1 , y1 , z1 ) e um vetor não nulo −
v = (a, b, c). Só existe
→
uma reta r que passa por A e tem a direção de −
v . Um ponto P (x, y, z) pertence a
−→
→
r se, e somente se, o vetor AP é paralelo a −
v , isto é,
−→
→
AP = t−
v
(4.1)
→
P = A + t−
v
(4.2)
(x, y, z) = (x1 , y1 , z1 ) + t(a, b, c)
(4.3)
para algum real t.
→
De 4.1, vem P − A = t−
v ou
ou, em coordenadas
Qualquer uma das equações 4.1, 4.2 ou 4.3 é denominada equação vetorial de r.
→
O vetor −
v é chamado vetor diretor da reta r e t é denominado parâmetro.
51
Exemplo 4.1.1. Determine a equação vetorial da reta r que passa pelo ponto A(3, 0, −5)
→
−
→
→ −
−
→
e tem a direção do vetor −
v =2 i +2j − k.
→
Seja P (x, y, z) um ponto genérico dessa reta, tem-se P = A + t−
v , isto é, (x, y, z) =
(3, 0, −5) + t(2, 2, −1).
Quando t varia de −∞ a +∞, P descreve a reta r. Assim, se t = 2, por exemplo:
(x, y, z) = (3, 0, −5)+t(2, 2, −1)
=⇒
(x, y, z) = (3, 0, −5)+(4, 4, −2)
=⇒
(x, y, z) = (7, 4, −7)
O ponto P (7, 4, −7) é um ponto da reta r. Reciprocamente, a cada ponto P ∈ r
corresponde um número real t. Por exemplo, sabe-se que o ponto P (7, 4, −7) pertence
à reta r : (x, y, z) = (3, 0, −5) + t(2, 2, −1), logo, é verdadeira a afirmação:
(7, 4, −7) = (3, 0, −5) + t(2, 2, −1), para algum número real t.
Dessa igualdade, vem:
t(2, 2, −1) = (7, 4, −7) − (3, 0, −5)
=⇒
t(2, 2, −1) = (4, 4, −2)
=⇒
(2t, 2t, −1t) = (4, 4, −2)
Da definição de igualdade de vetores, vem: t = 2.
Vamos agora apresentar uma outra maneira de escrever as equações de uma reta.
Da equação vetorial da reta (x, y, z) = (x1 , y1 , z1 ) + t(a, b, c) ou ainda (x, y, z) =
(x1 + at, y1 + bt, z1 + ct), pela condição de igualdade, obtém-se
x = x1 + at
y = y1 + bt
z = z + ct
1
As equações 4.1.2 são chamadas equações paramétricas da reta.
52
(4.4)
→
Exemplo 4.1.2. Dados o ponto A(2, 3, −4) e o vetor −
v = (1, −2, 3), pede-se:
→
a) Escrever equações paramétricas da reta r que passa por A e tem direção de −
v.
b) Encontrar o ponto B de r de parâmetro t = 1.
c) Determinar o ponto de r cuja abscissa é 4.
d) Verificar se os pontos D(4, −1, 2) e E(5, −4, 3) pertencem a r.
a) De acordo com a forma paramétrica da reta temos imediatamente:
x= 2+t
r:
y = 3 − 2t
z = −4 + 3t
b) Das equações acima tem-se para t = 1:
x = 2 + (1) = 3
y = 3 − 2(1) = 1
z = −4 + 3(1) = −1
Portanto, B(3, 1, −1) ∈ r
c) Como o ponto tem abscissa 4 (x = 4), temos
4 = 2 + t (1o equação de r) e, portanto,t = 2. Como t = 2 ,=⇒
y = 3 − 2(2) = −1
z = −4 + 3(2) = 2
O ponto procurado é (4, −1, 2).
d) Um ponto pertence à reta r se existe um real t que satisfaz as equações de r.
53
Para D(4, −1, 2) as equações
4= 2+t
−1 = 3 − 2t
2 = −4 + 3t
se verificam para t = 2 e, portanto, D ∈ r.
Vamos pensar o seguinte fato: Dados dois pontos, por exemplo, no espaço, como
determinar as equações paramétricas da reta que passa por esses pontos?
Observe que a reta definida pelos pontos A e B é a reta que passa por A (ou B) e tem
−→
→
direção do vetor −
v = AB.
Vejamos um exemplo.
0,3cm
Exemplo 4.1.3. Escrever equações paramétricas da reta r que passa por A(3, −1, −2) e
B(1, 2, 4).
x = 3 − 2t
−→
→
Escolhendo o ponto A e o vetor −
v = AB = B−A = (−2, 3, 6), tem-se r :
y = −1 + 3t
z = −2 + 6t
Das equações paramétricas
x = x1 + at
y = y1 + bt
z = z1 + ct
supondo abc ̸= 0, vem
t=
x − x1
a
t=
y − y1
b
t=
z − z1
c
Como para cada ponto da reta corresponde um só valor para t, obtemos as igualdades
x − x1
y − y1
z − z1
=
=
a
b
c
54
(4.5)
As equações 4.5 são denominadas equações simétricas da reta que passa pelo ponto
−
A(x1 , y1 , z1 ) e tem a direção do vetor →
v = (a, b, c).
→
Exemplo 4.1.4. A reta que passa pelo ponto A(3, 0, −5) e tem a direção do vetor −
v =
x−3
y
z+5
(2, 2, −1), tem equações simétricas
= =
.
2
2
−1
Se desejarmos obter outros pontos da reta, basta atribuir um valor qualquer a uma das
5−3
y
z+5
variáveis. Por exemplo, para x = 5, tem-se
=1= =
onde y = 2 e z = −6
2
2
−1
e, portanto, o ponto (5, 2, −6) pertence à reta.
Consideremos agora a seguinte situação
→
Seja a reta r definida pelo ponto A(2, −4, −3) e pelo vetor diretor −
v = (1, 2, −3) e
expressa pelas equações simétricas
r:
x−2
y−4
z+3
=
=
1
2
−3
(4.6)
A partir destas equações pode-se expressar duas variáveis em função da terceira. Isolando, primeiramente, as variáveis y e z e expressando-as em função de x, obtém-se
x−2
1
=
y+4
2
1(y + 4) = 2(x − 2)
x−2
1
=
z+3
−3
1(z + 3)
=
−3(x − 2)
y+4
= 2x − 4
z+3 =
−3x + 6
y
= 2x − 8
z
=
−3x + 3
(4.7)
Estas duas últimas equações são equações reduzidas da reta r, na variável x.
Observações
a) É fácil verificar que todo ponto P ∈ r é do tipo P (x, 2x − 8, −3x + 3), onde x pode
assumir um valor qualquer. Por exemplo, para x = 3 tem-se o ponto P1 (3, −2, −6) ∈
r.
55
b) Equações reduzidas na variável x serão sempre da forma
y = mx + n
z = px + q
c) Apartir das equações 4.6, pode-se obter as equações
x = 1y + 4
2
(equações reduzidas na variável y)
z = −3y − 9
2
ou
x = −1z + 1
3
(equações reduzidas na variável z).
2
y=
− z−6
3
d) Areta r das equações 4.6 pode ser representada pelas equações paramétricas
x= 2+t
y = −4 + 2t
z = −3 − 3t
Da primeira equação obtém-se t = x − 2 que, substituindo nas outras duas as transforma em
y = −4 + 2(x − 2) = 2x − 8
z = −3 − 3(x − 2) = −3x + 3
que são as equações reduzidas de 4.7.
e) Paraencontrar um vetor diretor da reta
y = 2x − 8
r:
z = −3x + 3
uma das formas é determinar dois pontos A e B de r e, posteriormente, encontrar o
−→
vetor AB = B − A. Por exemplo, para x = 0, obtém-se o ponto A(0, −8, 3) e para
x = 1, obtém-se o ponto B(1, −6, 0).
−→
Logo, AB = (1, 2, −3) é um vetor diretor de r.
Atividades
1. Verifique se os pontos P1 (5, −5, 6) e P2 (4, −1, 12) pertencem à reta r :
56
x−3
y+1
z−2
=
=
.
−1
2
−2
2. O ponto P (2, y, z) pertence à reta determinada por A(3, −1, 4) e B(4, −3, −1). Calcule P .
3. Determine as equações reduzidas, com variável independente x, da reta que passa
−
→
−
→
−
→
→
pelo ponto A(4, 0, −3) e tem a direção do vetor −
v =2 i +4j +5k.
x = 2t
4. Cite um ponto e um vetor diretor da reta r :
y = −1 .
z =2−t
5. Determine a equação da reta que passa por A(1, −2, 4) e é paralela ao eixo dos x.
4.2
Posições Relativas de Retas
Duas retas r1 e r2 , no espaço, podem ser:
a) concorrentes, isto é, situadas no mesmo plano. Nesse caso, as retas poderão ser:
(a) concorrentes: r1 ∩ r2 = {P } (P é o ponto de intersecção das retas r1 e r2 ;
(b) paralelas: r1 ∩ r2 = ∅ (∅ é o conjunto vazio)
57
→
A condição de paralelismo das retas r1 e r2 é a mesma dos vetores −
v1 =
−
(a1 , b1 , c1 ) e →
v = (a2 , b2 , c2 ), que definem as direções dessas retas, isto é:
a1
b1
c1
−
→
→
v1 = m−
v2 ou
=
=
a2
b2
c2
(O caso de serem r1 e r2 coincidentes pode ser considerado como um caso
particular de paralelismo).
b) reversas, isto é, não situadas no mesmo plano.
Nesse caso: r1 ∩ r2 = ∅
Observações
−−−→
−
→
A igualdade (→
v1 , −
v2 , A1 A2 ) = 0 é a condição de coplanaridade de duas retas r1 e
r2 que passam, respectivamente, pelos pontos A1 e A2 , e tem por vetores diretores
→
→
os vetores −
v1 e −
v2 :
−−−→
−
→
a) se r1 e r2 forem paralelas, serão coplanares, isto é, (→
v1 , −
v2 , A1 A2 ) = 0, pois
−−−→
→
→
duas linhas do determinante utilizado para calcular (−
v1 , −
v2 , A1 A2 ) apresentam
→
→
elementos proporcionais −
v1 = k −
v2 .
−−−→
→
→
b) se r1 e r2 não forem paralelas, a igualdade (−
v1 , −
v2 , A1 A2 ) = 0 exprime a
condição de concorrência dessas retas.
−−−→
→
→
c) se o determinante utilizado para calcular (−
v1 , −
v2 , A1 A2 ) for diferente de zero,
as retas r1 e r2 são reversas.
58
Exemplo 4.2.1. Estude a posição relativa das retas:
x = 1 − 3t
y = 2x − 3
r1 :
e r2 :
y = 4 − 6t
z = −x
z = 3t
−
→
→
São vetores diretores de r1 e r2 : →
v1 = (1, 2, −1) e −
v2 = (−3, −6, 3). Como −
v2 =
→
−3 · −
v1 , as retas r1 e r2 são paralelas e não coincidentes (basta ver que o ponto
A1 (0, −3, 0) ∈ r1 e A1 (0, −3, 0) ̸∈ r2 .
Exemplo 4.2.2. Estude a posição relativa das retas
x= 5+t
x−2
y
z−5
r1 :
= =
e r2 :
y = 2−t
2
3
4
z = 7 − 2t
As retas não são paralelas pois:
−−−→
2
3
4
→
→
̸=
̸=
. Calculemos o produto misto (−
v1 , −
v2 , A1 A2 )
1
−1
−2
para A1 (2, 0, 5) e A2 (5, 2, 7):
4
2 3
−
−
−
→
→
→
(−
v1 , −
v2 , A1 A2 ) =
1 −1 −2 = 0
3 2
2
o que significa que as retas r1 e r2 são concorrentes (se o determinante fosse diferente
de zero, as retas seriam reversas).
Conhecidas as equações de duas retas, podemos determinar o seu ponto de intersecção.
Duas retas r1 e r2 coplanares e não paralelas são concorrentes. Consideremos as retas:
x = −t
y = −3x + 2
e r2 :
r1 :
y = 1 + 2t
z = 3x − 1
z = −2t
59
e determinemos o seu ponto de intersecção. Se I(x, y, z) é este ponto, suas coordenadas satisfazem o sistema formado pelas equações de r1 e r2 , isto é, I(x, y, z) é a
solução do sistema:
y=
z=
x=
y=
z=
−3x + 2
3x − 1
−t
1 + 2t
−2t
Eliminando t nas três últimas equações, temos o sistema equivalente
y = −3x + 2
z = 3x − 1
y = 1 − 2x
z = 2x
Resolvendo o sistema, encontramos:
x= 1
y = −1
z= 2
Logo, o ponto de intersecção das retas r1 e r2 é: I(1, −1, 2).
4.3
Ângulos entre Retas
Sejam as retas r1 , que passa pelo ponto A1 (x1 , y1 , z1 ) e tem direção de um vetor
−
→
v1 = (a1 , b1 , c1 ), e r2 , que passa pelo ponto A2 (x2 , y2 , z2 ) e tem direção de um vetor
−
→
v2 = (a2 , b2 , c2 ).
60
Definição 4.3.1. Chama-se ângulo de duas retas r1 e r2 o menor ângulo de um vetor
diretor de r1 e de um vetor diretor de r2 . Logo, sendo θ este ângulo, tem-se
→
→
|−
v1 · −
v2 |
π
cos θ = −
, com 0 ≤ θ ≤
→
→
−
2
| v1 || v2 |
(4.8)
ou, em coordenadas:
|a1 a2 + b1 b2 + c1 c2 |
√
cos θ = √ 2
a1 + b21 + c21 a22 + b22 + c22
Observação
Na figura, o ângulo α é suplementar de θ e, portanto, cos α = cos θ. O ângulo α é
→
→
→
→
o ângulo formado por −−
v1 e −
v2 ou −
v1 e −−
v2 .
Exemplo 4.3.1. Calcular o ângulo entre as retas
x= 3+t
x+2
y−3
z
e r2 :
=
=
r1 :
y
=
t
−2
1
1
z = −1 − 2t
→
Os vetores que definem as direções das retas r1 e r2 são, respectivamente: −
v1 =
→
(1, 1, −2) e −
v2 = (−2, 1, 1). Logo, temos
→
→
|−
v1 · −
v2 |
|(1, 1, 2) · (−2, 1, 1)|
√
cos θ = −
=√
→
−
→
2
2
| v1 || v2 |
1 + 1 + (−2)2 × (−2)2 + 12 + 12
61
cos θ = √
1
| − 2 + 1 − 2|
| − 3|
3
√
√ = =
=√
6
2
1+1+4× 4+1+1
6× 6
→
→
Observemos que duas retas r1 e r2 com as direções de −
v1 e −
v2 , respectivamente, são
ortogonais se:
→
→
r1 ⊥ r2 ⇐⇒ −
v1 · −
v2 = 0
Duas retas ortogonais podem ser concorrentes ou não. Na figura anterior, as retas r1
e r2 são ortogonais a r, porém, r2 e r são concorrentes. Nesse caso, diz-se que são
perpendiculares.
Exemplo 4.3.2. Verifique se as retas
r1 :
y = −2x + 1
z = 4x
x = 3 − 2t
e r2 :
y = 4+t
z= t
são ortogonais.
→
−
Sendo −
v1 = (1, −2, 4) e →
v2 = (−2, 1, 1) vetores diretores de r1 e r2 tem-se:
−
→
→
v1 · −
v2 = 1(−2) − 2(1) + 4(1) = 0, portanto as retas r1 e r2 são ortogonais.
62
→
−
Agora, sejam as retas r1 e r2 não paralelas, com as direções de −
v1 e →
v2 , respectivamente. Toda reta r ao mesmo tempo ortogonal a r1 e r2 terá a direção de um vetor
−
→
v tal que
−
→
→
v ·−
v1 = 0
−
→
→
v ·−
v2 = 0
(4.9)
→
Em vez de tomarmos um vetor −
v =
̸ 0 como uma solução particular do sistema 4.9,
→
→
→
poderíamos utilizar o produto vetorial, isto é, −
v =−
v1 × −
v2 .
Definido um vetor diretor, a reta r estará determinada quando for conhecido um de
seus pontos.
Exemplo 4.3.3. Determine equações paramétricas da reta r que passa pelo ponto
A(3, 4, −1) e é ortogonal às retas
r1 : (x, y, z) = (0, 0, 1) + t(2, 3, −4) e r2 :
x=5
y=t
z =1−t
→
→
As direções de r1 e r2 são definidas pelos vetores −
v1 = (2, 3, −4) e −
v2 = (0, 1, −1).
Então a reta r tem a direção do vetor
→
−
→ −
→ −
k
i j
−
→
→
v1 × −
v2 =
2 3 −4 = (1, 2, 2)
0 1 −1
Logo, tem-se
x= 3+t
r:
y = 4 + 2t
z = −1 + 2t
63
Atividades
1) Determine o ângulo entre as retas
x = −2 − 2t
r:
y = 2t
z = 3 − 4t
2) A reta r :
es:
y+6
z−1
x
=
=
.
4
2
2
y = mx + 3
é ortogonal à reta determinada pelos pontos A(1, 0, m)
z =x−1
e B(−2, 2m, 2m). Calcule o valor de m.
4.4
Distância de Ponto a Reta
Dado um ponto P do espaço e uma reta r, quer-se calcular a distância d(P, r) de P
−→
→
→
a r. Consideremos na reta r um ponto a e um vetor diretor −
v . Os vetores −
v e AP
determinam um paralelogramo cuja altura corresponde à distância d(P, r).
A área A do paralelogramo é dada por
→
a) A = (base) · (altura) = |−
v | · d ou
−→
→
b) A = |−
v × AP |.
64
Comparando a) e b), vem
−→
→
|−
v × AP |
d = d(r1 , r2 ) =
→
|−
v|
Exemplo 4.4.1. Calcule a distância
r:
(4.10)
do ponto P (2, 1, 4) à reta
x = −1 + 2t
y = 2−t
z = 3 − 2t
→
A reta r passa pelo ponto A(−1, 2, 3) e tem a direção do vetor −
v = (2, −1, −2). Seja
−→
ainda o vetor AP = P − A = (3, −1, 1). Calculemos
−
→ −
→ −
→
j
j
i
−→
−
→
= (−3, −8, 1)
v × AP =
2
−1
−2
3 −1 1
√
√
(−3)2 + (−8)2 + 12
74
|(−3, −8, 1)|
=
=√
u.c.
Logo temos d(P, r) =
|(2, −1, −2)|
3
22 + (−1)2 + (−2)2
Podemos utilizar do fato de que sabemos calcular a distância de um ponto a uma reta
para calcularmos a distância entre duas retas paralelas.Dadas as retas r1 e r2 , quer-se
calcular a distância d(r1 , r2 ). Podemos ter os seguintes casos:
(a) r1 e r2 são concorrentes.
Neste caso : d(r1 , r2 ) = 0.
(b) r1 e r2 são paralelas.
d(r1 , r2 ) = d(P, r2 ), com P ∈ r1 ou d(r1 , r2 ) = d(P, r1 ) com P ∈ r2 .
A figura a seguir ilustra esta situação, que se reduz ao cálculo da distância de
ponto à reta.
65
(c) r1 e r2 são reversas.
→
Seja r1 a reta definida pelo ponto A1 e pelo vetor diretor −
v1 e a reta r2 pelo ponto
→
A2 e pelo vetor diretor −
v2 .
−−−→
→
→
Os vetores −
v1 , −
v2 e A1 A2 , por serem não coplanares, determinam um paralelepípedo (figura ??) cuja altura é a distância d(r1 , r2 ) que se quer calcular (a reta r2
→
→
é paralela ao plano da base do paralelepípedo definida por −
v1 e −
v2 ).
Exemplo 4.4.2. Calcule a distância entre as retas
x = −1 + t
y = x−3
r1 :
e
r
:
2
y = 3 − 2t
z = −x + 1
z = 1−t
→
A reta r1 passa pelo ponto A1 (−1, 3, 1) e tem a direção de −
v1 = (1, −2, −1) e a
→
reta r2 pelo ponto A2 (0, −3, 1) e tem a direção de −
v2 = (1, 1, −1).
66
−−−→
Então, A1 A2 = A2 − A1 = (1, −6, 0) e
1 −2 −1
−−−→
→
→
=3
(−
v1 , −
v2 , A1 A2 ) =
1
1
−1
1 −6 0
− −
→
→ −
→
j
j
i
→
−
→
= (3, 0, 3)
v1 × −
v2 =
1
−2
−1
1 1 −1
√
√
√
√
3
3
32 · 6
6
|3|
√ =
=√
Então temos d(r1 , r2 ) =
=√ =√
2
2
|(3, 0, 3)|
6
3 +3
18
18 · 18
Atividades
x = 1 − 2t
.
1) Calcule a distância do ponto P (1, 2, 3) à reta s :
y = 2t
z =2−t
2) Calcule a distância entre as retas r :
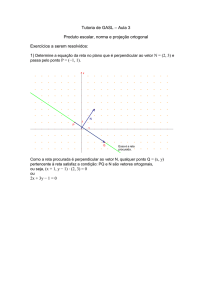
67
x=0
y=z
es:
y=3
z = 2x
.
capítulo
Planos
Objetivos
• Identificar a equação de um plano;
• Determinar a equação de um plano sobre diferentes circunstâncias;
• Determinar a interseção de uma reta com um plano;
• Reconhecer planos paralelos e perpendiculares;
• Determinar o ângulo formado entre dois planos;
• Calcular a distância de um ponto a um plano.
69
5
5.1
Equação de um Plano
→
→
Seja A(x1 , y1 , z1 ) um ponto pertencente a um plano π e −
n = (a, b, c), −
n =
̸ 0, um
vetor normal (ortogonal) ao plano.
−
−
Como →
n ⊥ π, →
n é ortogonal a todo vetor representado em π. então, um ponto
−→
→
P (x, y, z) pertence a π se, e somente se, o vetor AP é ortogonal a −
n , isto é,
−
→
n · (P − A) = 0
ou
(a, b, c) = (x − x1 , y − y1 , z − z1 ) = 0
ou
a(x − x1 ) + b(y − y1 ) + c(z − z1 ) = 0
ou, ainda
ax + by + cz − ax1 − by1 − cz1 = 0
Fazendo −ax1 − by1 − cz1 = d, obtemos
ax + by + cz + d = 0
Esta é a equação geral do plano π.
Observações
71
(5.1)
→
−
a) Assim como −
n = (a, b, c) é um vetor normal a π, qualquer vetor k →
n , k ̸= 0,
é também vetor normal ao plano.
b) É importante notar que os três coeficientes a, b e c da equação 5.1 representam
as componentes de um vetor normal ao plano.
Por exemplo, se um plano π é dado por π : 3x + 2y − z + 1 = 0, um de seus
−
vetores normais é →
n (3, 2, −1).
c) Para obter pontos de um plano dado por uma equação geral, basta atribuir
valores arbitrários a duas das variáveis e calcular o valor da outra na equação
dada.
Assim, por exemplo, se na equação anterior fizermos x = 4 e y = −2, teremos:
3(4) + 2(−2) − z + 1 = 0 =⇒ 12 − 4 − z + 1 = 0 =⇒ z = 9
e, portanto, o ponto A(4, −2, 9) pertence a este plano.
Exemplo 5.1.1. Obtenha uma equação geral do plano π que passa pelo ponto
−
A(2, −1, 3) e tem →
n = (3, 2, −4) como um vetor normal.
→
Como −
n é normal a π, sua equação é do tipo:
3x + 2y − 4z + d = 0
e sendo A um ponto do plano, suas coordenadas devem verificar a equação, isto é
3(2) + 2(−1) − 4(3) + d = 0 =⇒ 6 − 2 − 12 + d = 0 =⇒ d = 8
Logo, uma equação geral do plano π é 3x + 2y − 4z + 8 = 0.
Observação
Se um plano π intercepta os eixos coordenados nos pontos (p, 0, 0), (0, q, 0) e (0, 0, r)
72
com p · q · r ̸= 0, então π admite a equação
x y z
+ + =1
p q r
denominada equação segmentária do plano π.
Vamos considerar agora um ponto A(x0 , y0 , z0 ) um ponto pertencente a um plano
→
→
π e −
u = (a1 , b1 , c1 ) e −
v = (a2 , b2 , c2 ) dois vetores paralelos a π (figura 5.2),
→
→
porém, −
u e−
v não-paralelos.
−→ → −
Para todo ponto P do plano, os vetores AP , −
u e→
v são coplanares. Um ponto
P (x, y, z) pertence a π se, e somente se, existem números reais h e t tais que
→
→
P − A = h−
u + t−
v
ou
→
→
P = A + h−
u + t−
v
ou, em coordenadas
(x, y, z) = (x0 , y0 , z0 ) + h(a1 , b1 , c1 ) + t(a2 , b2 , c2 ), h, t ∈ ℜ
(5.2)
→
→
Esta equação é denominada equação vetorial do plano π. Os vetores −
u e−
v são
vetores diretores de π.
Da equação 5.2 obtém-se
(x, y, z) = (x0 + a1 h + a2 t, y0 + b1 h + b2 t, z0 + c1 h + c2 t)
que pela condição de igualdade,
x=
y=
z=
vem
x0 + a1 h + a2 t
y0 + b1 h + b2 t
z0 + c1 h + c2 t, h, t ∈ ℜ
73
Estas equações são chamadas equações paramétricas de π e h e t são variáveis
auxiliares denominadas parâmetros.
Exemplo 5.1.2. Seja o plano π que passa pelo ponto A(2, 2, −1) e é paralelo aos
→
→
vetores −
u = (2, −3, 1) e −
v = (−1, 5, −3). Obtenha uma equação vetorial, um
sistema de equações paramétricas e uma equação geral de π
• Equação vetorial: (x, y, z) = (2, 2, −1) + h(2, −3, 1) + t(−1, 5, −3).
• Equações paramétricas:
x = 2 + 2h − t
y = 2 − 3h + 5t
z = −1 + h − 3t
Observação: Se quisermos algum ponto deste plano, basta atribuir valores
reais para h e t. Por exemplo, para h = 0 e t = 1, vem: x = 1, y = 7 e z = −4.
E, portanto, B(1, 7, −4) é um ponto do plano π.
• Equação geral: Como o vetor
→
−
→ −
→ −
j
k
i
−
→
→
= (4, 5, 7)
u ×−
v =
2
−3
1
−1 5 −3
→
→
→
é simultaneamente ortogonal a −
u e−
v , ele é um vetor −
n normal ao plano π.
Então, uma equação geral de π é da forma 4x + 5y + 7z + d = 0 e, como A ∈ π
tem-se: 4(2) + 5(2) + 7(−1) + d = 0 =⇒ d = −11. Portanto, uma equação geral
do plano π é dada por 4x + 5y + 7z − 11 = 0.
Exemplo 5.1.3. Dado o plano π determinado pelos pontos A(1, −1, 2), B(2, 1, −3)
e C(−1, −2, 6), obtenha um sistema de equações paramétricas e uma equação geral
de π.
74
• Equações paramétricas:
Sabe-se que existe apenas um plano que contém três pontos não em linha reta.
−→
−→
→
→
Os vetores não-paralelos −
u = AB = (1, 2, −5) e −
v = AC = (−2, −1, 4) são
vetores diretores de api e, portanto,
x=
y=
z=
as equações (utilizando o ponto A)
1 + h − 2t
−1 + 2h − t
2 − 5h + 4t
são equações paramétricas do plano
−
• Equação geral: Sendo →
u e v vetores
−
→
i
−
→
→
u ×−
v =
1
−2
diretores de π, o vetor
→
−
→ −
j
k
2 −5
= (3, 6, 3)
−1 4
é um vetor normal a π. Então, uma equação geral é da forma 3x+6y +3z +d =
0. Como A ∈ π (poderíamos tomar B ou C): 3(1) + 6(−1) + 3(2) + d = 0 =⇒
d = −3. Portanto, uma equação geral de π é 3x + 6y + 3z − 3 = 0, ou
multiplicando ambos os membros da equação por 1/3: x + 2y + z − 1 = 0.
Observações
a) Como é possível encontrar infinitos ternos A, B e C de pontos não alinhados
em π, existem infinitos sistemas de equações paramétricas que representam o
mesmo plano.
b) É importante observar que os vetores diretores sejam não-paralelos. Se ocorrer
−→ −→
−→ −→
AB//AC, basta trocar um dos pontos de modo a garantir que AB e AC sejam
não-paralelos.
75
c) Uma outra maneira de obter equações paramétricas a partir da equação geral, é
substituindo duas das variáveis pelos parâmetros h e t e, posteriormente, isolar
a terceira variável em função destes.
Por exemplo, se na equação geral 2x − y − z + 4 = 0, fizermos y = h e z = t,
1
1
teremos 2x − h − t + 4 = 0. Isolando x resulta, x = −2 + h + t. Então,
2
2
x = −2 + 21 h + 12 t
y= h
z= t
são equações paramétricas do plano.
Atividade
1) Dado o plano π determinado pelos pontos A(2, −1, 3), B(1, 1, −1) e C(−3, −2, 2),
obtenha um sistema de equações paramétricas e uma equação geral de π.
5.2
Posições relativas de reta e plano
−
→
Sejam →
v um vetor diretor da reta r, −
n um vetor normal ao plano π e P um
ponto. As posições de uma reta r com o plano π são:
i. r paralela a π
→
→
r//π ⇐⇒ −
v ·−
n = 0 e P ̸∈ π
ii. r contida em π
→
→
r ⊂ π ⇐⇒ −
v ·−
n =0eP ∈π
76
iii. r e π concorrentes (ou transversais)
→
→
r ∩ π = {P } ⇐⇒ −
v ·−
n ̸= 0
Exemplo 5.2.1. Determine a intersecção da reta r com o plano π, nos seguintes casos:
a)
r : (x, y, z) = (1, 6, 2) + t(1, 1, 1); t ∈ ℜ
π :x−z−3=0
b)
r : x − 1 = y − 2 = 2(z − 1)
π : (x, y, z) = h(6, 2, 1) + t(1, 2, 1); t, h ∈ ℜ
77
x= t
r:
y = −3 + 3t ; t ∈ ℜ
c)
z = −t
π : x + y + 2z − 1 = 0
→
→
a) −
v ·−
n = (1, 1, 1) · (1, 0, −1) = 0. Logo, r ∩ π = r ou r ∩ π = ∅.
Como P (1, 6, 2) é um ponto de r, verificamos que P ̸∈ π.
Portanto, r ∩ π = ∅ e conclui-se que r e π são paralelos.
1
−
→
b) Sendo →
v = (1, 1, ) e −
n = (6, 2, 1) × (1, 2, 1) = (0, −5, 10), temos que
2
−
→
→
v ·−
n = 0. Logo, r ∩ π = r ou r ∩ π = ∅.
Como P (1, 2, 1) é um ponto de r, verificamos que P ∈ π.
Portanto, r ∩ π = r e conclui-se que r está contida em π.
→
→
c) De −
v ·−
n = (1, 3, −1)·(1, 1, 2) = 2 ̸= 0 concluímos que r π são concorrentes.
Seja r ∩ π = {P } = {(a, b, c)}. Temos
então:
a= t
(1)
a + b + 2c − 1 = 0 e (2)
b = −3 + 3t
c = −t
De (1) e (2) obtemos t = 2 e P (2, 3, −2).
para algum escalar t
Atividade
1) Determine o ponto de interseção da reta r : (x = t, y = 1 − 2t, z = −t) com
o plano π : 2x + y − z − 4 = 0.
78
5.3
Posições Relativas de Planos
Sejam π1 : a1 x + b1 y + c1 z + d1 = 0 e π2 : a2 x + b2 y + c2 z + d2 = 0 dois planos
quaisquer:
a) π1 e π2 são paralelos se, e somente se, a1 , b1 , c1 e a2 , b2 , c2 são proporcionais.
b) Nas condições do item (a):
• se d1 = d2 estão na mesma proporção, isto é, se a1 , b1 , c1 , d1 e a2 , b2 , c2 , d2
são proporcionais, então π1 = π2 .
• se d1 = d2 não seguem a proporcionalidade de a1 , b1 , c1 , d1 e a2 , b2 , c2 , d2 ,
então π1 e π2 são paralelos distintos.
c) π1 e π2 são concorrentes (ou transversais) se, e somente se, a1 , b1 , c1 , d1 e
a2 , b2 , c2 , d2 não são proporcionais.
Exemplo 5.3.1. Estude a posição relativa dos planos:
79
a) π1 : 2x + y − z + 1 = 0 e π2 : 4x + 2y − 2z + 2 = 0.
b) π1 : (x, y, z) = (1, 0, 1)+h(0, 0, 1)+t(2, 1, 3); t, h ∈ ℜ e π2 : 2x+y−z+1 = 0
x = 4t
c) π1 : (x, y, z) = (1, 0, 1)+h(0, 0, 1)+t(2, 1, 3); t, h ∈ ℜ e π2 :
; t∈
y = 1 + 2t
z = 2 − h + 5t
→
→
a) Observemos que −
n = 2−
n , assim os planos π e π são paralelos. Além
π1
π2
1
2
disso, temos d1 = 2d2 .
Portanto, podemos concluir que π1 e π2 são coincidentes.
→
→
b) Consideremos os vetores −
n π1 = (2, 1, 3) × (0, 0, 1) = (1, −2, 0) e −
n π2 =
(2, 1, −1).
Como estes vetores não são paralelos, temos que os planos π1 e π2 são concorrentes.
→
→
c) Consideremos os vetores −
n π1 = (1, −2, 0) e −
n π1 = (−2, 4, 0). Observemos
→
→
que −
n π1 = −2−
n π2 , daí os planos π1 e π2 são paralelos. No entanto, P (1, 0, 1)
pertence ao plano π1 e não pertence ao plano π2 .
Consequentemente, π1 e π2 são estritamente paralelos.
Podemos determinar o ponto de intersecção de uma reta com um plano. Observe o exemplo a seguir:
Exemplo 5.3.2. Determine o ponto de intersecção da reta r com o plano π,
80
em que
x = −1 + 2t
r:
y = 5 + 3t
z = 4 − 2t
e
π : 2x − y + 3z − 4 = 0
Qualquer ponto de r é da forma (x, y, z) = (−1 + 2t, 5 + 3t, 3 − t). Se um deles
é comum ao plano π, suas coordenadas verificam a equação de π:
2(−1 + 2t) − (5 + 3t) + 3(3 − t) − 4 = 0
e daí resulta t = −1.
Substituindo este valor nas equações de r obtém-se:
x = −1 + 2(−1) = −3,
y = 5 + 3(−1) = 2,
z = 3 − (−1) = 4
Logo, a intersecção de r e π é o ponto (−3, 2, 4).
Observe agora, um exemplo em que estamos interessados em determinar a intersecção de dois planos.
Exemplo 5.3.3. Sejam os planos não-paralelos
π1 : 5x − y + z − 5 = 0
e
π2 : x + y + 2z − 7 = 0
A intersecção de dois planos não paralelos é uma reta r cujas equações se deseja
determinar. Para tanto, dentre os vários procedimentos, apresentaremos dois.
A. Como r está contida nos dois planos, as coordenadas de qualquer ponto
(x, y, z) ∈ r devem satisfazer simultaneamente as equações dos dois planos.
Logo, os pontos de r constituem a solução do sistema:
5x − y + z − 5 = 0
r:
x + y + 2z − 7 = 0
81
(5.3)
O sistema tem infinitassoluções (são os infinitos pontos de r) e, em termos
y = 3x − 1
de x, sua solução é r :
que são equações reduzidas de r.
z = −2x + 4
B. Outra maneira de obter equações de r é determinar um de seus pontos e um
vetor diretor.
Seja determinar o ponto A ∈ r que tem abscissa zero. Então fazendo x = 0
nas
equações do sistema 5.3 resulta o sistema
−y + z − 5 = 0
y + 2z − 7 = 0
cuja solução é y = −1 e z = 4. Logo, A(0, −1, 4).
→
→
Como um vetor diretor −
v de r é simultaneamente ortogonal a −
n1 = (5, −1, 1)
−
e→
n2 = (1, 1, 2), normais aos planos π1 e π2 , respectivamente (figura ??), o
→
vetor −
v pode ser dado por
→
−
→ −
→ −
j
k
i
−
→
→
→
= (−3, −9, 6)
v =−
n1 × −
n2 =
5
−1
1
1 1 2
1
ou também − (−3, −9, 6) = (1, 3, −2).
3
Escrevendo equações paramétricas de r, temos:
x= t
r:
y = −1 + 3t
z = 4 − 2t
82
Atividade
1) Determine as equações paramétricas da reta interseção dos planos π1 : 2x −
y − 3z + 5 = 0 e π2 : x + y − z − 3 = 0.
2) Determine a e b, de modo que os planos π1 : ax + by + 4z − 1 = 0 e
π2 : 3x − 5y − 2z + 5 = 0 sejam paralelos.
5.4
Ângulo entre Reta e Plano
−
→
Seja uma reta r com a direção do vetor →
v e um plano π, sendo −
n um vetor
normal a π.
O ângulo ϕ da reta r com o plano π é o complemento do ângulo θ que a reta r
forma com uma reta normal no plano.
83
π
e, portanto, cos θ = sen ϕ, e com isso, temos
2
→
→
|−
v ·−
n|
π
sen ϕ = −
, 0≤ϕ≤
→
−
→
2
| v || n |
Tendo em vista que θ + ϕ =
x = 1 − 2t
Exemplo 5.4.1. Determinar o ângulo que a reta r :
forma
y = −t
z = 3+t
com o plano π : x + y − 5 = 0.
→
−
A reta r tem a direção do vetor −
v = (−2, −1, 1) e →
n = (1, 1, 0) é um vetor
normal ao plano π. Assim, tem-se:
√
→
→
|(−2, −1, 1) · (1, 1, 0)|
| − 2 − 1 + 0|
3
3
|−
v ·−
n|
√ √
√
=√
=
= √ =
sen ϕ = −
→
→
−
2
| v || n |
6 2
2 3
(−2)2 + (−1)2 + 12 12 + 12 + 02
5.5
Ângulo entre Dois Planos
Sejam os planos π1 : a1 x + b1 y + c1 z + d1 = 0 e π2 : a2 x + b2 y + c2 z + d2 =
−
→
0. Então, →
n1 = (a1 , b1 , c1 ) e −
n2 = (a2 , b2 , c2 ) são vetores normais a π1 e π2 ,
respectivamente.
Chama-se ângulo de dois planos π1 e π2 o menor ângulo que um vetor normal
de π1 forma com um vetor normal de π2 . Sendo θ este ângulo, tem-se:
→
→
|−
n1 · −
n2 |
π
cos θ = −
, com 0 ≤ θ ≤
→
−
→
2
|n1 ||n2 |
84
(5.4)
ou, em coordenadas:
|a1 a2 + b1 b2 + c1 c2 |
√
a21 + b21 + c21 a22 + b22 + c22
π
Como cos θ ≥ 0 quando 0 ≤ θ ≤ , o numerador de 5.4 deve ser positivo,
2
razão pela qual tomou-se o produto escalar em módulo, pois que este poderá ser
cos θ = √
negativo quando o ângulo entre os vetores for o suplementar de θ.
Exemplo 5.5.1. Determine o ângulo entre os planos π1 : 2x + y − z + 3 = 0
e π2 : x + y − 4 = 0
→
→
Sendo −
n1 = (2, 1, 1) e −
n2 = (1, 1, 0) vetores normais a π1 e π2 , de acordo com
5.4 tem-se
√
|2 + 1 + 0|
|(2, 1, 1) · (1, 1, 0)|
3
3
3
√
= √ √
cos θ = √
=√ = √ =
2
2
2
2
2
2
6 2
12
2 3
2 + 1 + (−1) · 1 + 1
√
3
π
Logo, θ = arc cos(
)= .
2
6
Como verificar, a partir de suas equações, se dois planos são perpendiculares?
→
→
Consideremos os planos π1 e π2 , e sejam −
n1 e −
n2 vetores normais a π1 e π2 ,
respectivamente. Logo
→
→
→
→
π1 ⊥ π2 ⇐⇒ −
n1 ⊥ −
n2 ⇐⇒ −
n1 · −
n2 = 0
Exemplo 5.5.2. Verificar se π1 : 3x + y − 4z + 2 = 0 e π2 : 2x + 6y + 3z = 0
são planos perpendiculares.
→
−
Sendo −
n1 = (3, 1, −4) e →
n2 = (2, 6, 3) vetores normais a π1 e π2 , respectivamente, e como
−
→
→
n1 · −
n2 = 3(2) + 1(6) − 4(3) = 0
85
conclui-se que π1 e π2 são perpendiculares.
Atividades
1) Determine o ângulo entre os planos π1 : x + 2y + z − 10 = 0 e π2 : 2x + y −
z + 1 = 0.
2) Determine o valor de m de modo que os planos π1 : 2mx + 2y − z = 0 e
π2 : 3x − my + 2z − 1 = 0 sejam perpendiculares.
5.6
Distância de Ponto a Plano
Sejam um ponto P0 (x0 , y0 , z0 ) e um plano π : ax + by + cz + d = 0.
Sejam A o pé da perpendicular conduzida por P0 sobre o plano π e P (x, y, z)
um ponto qualquer desse plano.
−−→
→
O vetor −
n (a, b, c) é normal ao plano π e, por conseguinte, o vetor AP0 tem a
→
mesma direção de −
n.
A distância d do ponto P0 ao plano π é:
−−→
d(P0 , π) = |AP0 |
86
−−→
−−→
→
Observando que o vetor AP0 é a projeção do vetor P P0 na direção de −
n , de
acordo com o dispositivo em 3.5, vem:
→
−−→ −
−−→
n d(P0 , π) = |AP0 | = P P0 · −
|→
n |
mas
−−→
P P0 = (x0 − x, y0 − y, z0 − z)
e
logo
−
→
n
(a, b, c)
= 2
−
→
a + b2 + c2
|n|
(a,
b,
c)
d(P0 , π) = (x0 − x, y0 − y, z0 − z) · √
a2 + b2 + c2 |a(x0 − x) + b(y0 − y) + c(z0 − z)|
√
d(P0 , π) =
a2 + b2 + c2
|ax0 + by0 + cz0 − ax − by − cz|
√
d(P0 , π) =
a2 + b2 + c2
Em virtude de P pertencer ao plano π:
−ax − by − cz = d
e, portanto
d(P0 , π) =
|ax0 + by0 + cz0 + d|
√
a2 + b2 + c2
87
(5.5)
Examinando esta fórmula, vê-se que o numerador é o módulo do número que
se obtém substituindo x, y e z no primeiro membro da equação geral do plano
pela coordenadas do ponto P0 , e o denominador é o módulo do vetor normal ao
plano.
Observação
Se o ponto considerado for a origem O(0, 0, 0) do sistema, tem-se:
d(O, π) = √
a2
|d|
+ b2 + c2
Exemplo 5.6.1. Calcule a distância do ponto P0 (−4, 2, 5) ao plano π : 2x +
y + 2z + 8 = 0.
No caso presente tem-se:
I) coordenadas do ponto P0 : x0 = −4, y0 = 2 e z0 = 5
−
II) componentes do vetor normal →
n : a = 2, b = 1 e c = 2
Substituindo esse valores em 5.5, vem:
d(P0 , π) =
|2(−4) + 1(2) + 2(5) + 8|
| − 8 + 2 + 10 + 8|
12
√
√
=
=
= 4 u.c.
3
4+1+4
22 + 12 + 22
Como caso particular da distância entre ponto e plano, podemos calcular a
distância entre dois planos.Essa distância só estará definida quando os planos
forem paralelos.
Dados dois planos π1 e π2 , paralelos, a distância d entre eles é a distância de
um ponto qualquer de um dos planos ao outro:
d(π1 , π2 ) = d(P0 , π2 ) com P0 ∈ π1
ou
d(π1 , π2 ) = d(P0 , π1 ) com P0 ∈ π2
88
Como se vê, a distância entre dois planos paralelos se reduz ao cálculo da
distância de um ponto a um plano.
Exemplo 5.6.2. Calcule a distância entre os planos π1 : 2x − 2y + z − 5 = 0
e π2 : 4x − 4y + 2z + 14 = 0
→
Um ponto de π1 é P0 (0, 0, 5) e um vetor normal a π2 é −
n = (4, −4, 2). Portanto,
de acordo com 5.5, vem:
d(π1 , π2 ) = d(P0 , π2 ) =
|4(0) − 4(0) + 2(5) + 14|
|10 + 14|
24
√
= √
=
u.c.
6
36
42 + (−4)2 + 22
Atividades
1) Calcule a distância do ponto P (2, −3, 5) ao plano π : 3x + 2y + 6z − 2 = 0.
2) Calcule a distância entre os planos paralelos π1 : x − 2z + 1 = 0 e π2 :
3x − 6z − 8 = 0.
3) Determine a distância da reta r :
x=3
y=4
ao plano π : x + y − 12 = 0.
4) Dado o tetraedro de vértices A(1, 2, 1), B(2, −1, 1), C(0, 1, −1) e D(3, 1, 0),
calcule a medida da altura baixada do vértice D ao plano da face ABC.
89
capítulo
6
Mudança de Coordenadas
Objetivos
• Reconhecer coordenadas polares, cilíndricas e esféricas;
• Efetuar mudança de coordenadas;
• Determinar rotações e translações no plano.
91
6.1
Coordenadas Polares
Até aqui, localizamos um ponto no plano por suas coordenadas cartesianas retangulares, em que um ponto do plano é localizado em relação a duas retas fixas
perpendiculares entre si. Há outros sistemas de coordenadas que dão origem a
posição de um ponto em um plano. O sistema de coordenadas polares é
um deles, em que um ponto do plano é localizado em relação a um ponto e a
uma reta que passa por esse ponto.
No sistema polar, as coordenadas consistem em uma distância orientada e na
medida de um ângulo relativo a um ponto fixo e a um semieixo fixo. Escolhemos um ponto O (usualmente a origem do sistema cartesiano), chamado pólo
e uma reta orientada passando pelo polo chamada eixo polar (usualmente tomamos o próprio eixo x do sistema cartesiano). Seja P um ponto qualquer no
plano, distinto de O. No sistema de coordenadas polares, um ponto no plano
é localizado dando-se a distância do ponto ao polo, r = dist(P, O) e o ângulo,
−→
θ, entre os vetores OP e um vetor na direção e sentido do eixo polar, com a
mesma direção e sentido do eixo polar, com a mesma convenção da trigonometria, ou seja, ele é positivo se medido no sentido anti-horário, a partir do
eixo polar e negativo se medido no sentido horário a partir do eixo polar. As
93
coordenadas polares de um ponto P do plano são escritas na forma (r, θ).
Segue facilmente as relações entre as coordenadas cartesianas e as coordenadas
polares.
Suponha que o polo e o eixo polar do sistema de coordenadas polares coincidem
com a origem e o eixo x do sistema de coordenadas cartesianas, respectivamente. Então, a transformação entre os sistemas de coordenadas polares e o
de coordenadas cartesianas pode ser realizada pelas equações
x = r cos θ
r=
cos θ = √
x
x2 + y 2
e
e
y = r sen θ
√
x2 + y 2
sen θ = √
y
x2 + y 2
, se
√
x2 + y 2 ̸= 0.
Estendemos as coordenadas polares para o caso no qual r é negativo da seguinte
forma:
(r, θ) = (|r|, θ + π), para r < 0.
Assim, (r, θ) e (−r, θ) estão na mesma reta que passa pelo pólo, à distância |r|
do pólo, mas em lados opostos em relação ao pólo.
Exemplo 6.1.1. Encontre as coordenadas cartesianas retangulares para o ponto
cujas coordenadas polares são (−6, 7π/4).
√
√
7π
2
x = r cos θ = −6 cos
= −6 ·
= −3 2
4
2√
√
7π
2
y = r sen θ = −6 sen
= −6 · −
=3 2
4
2
√ √
Assim, o ponto é (−3 2, 3 2).
Exemplo 6.1.2. Escreva a equação x2 + y 2 − 4x = 0 em coordenadas polares.
Substituindo x = r cos θ e y = r sen θ temos: r2 cos2 θ + r2 sen2 θ − 4rcos θ =
0 =⇒ r2 − 4rcos θ = 0 =⇒ r(r − 4cos θ) = 0.
94
Logo, r = 0 ou r(r − 4cos θ) = 0. O gráfico de r = 0 é a origem, contudo, ela
é um ponto do gráfico de r(r − 4cos θ) = 0 pois r = 0 quando θ = π/2. Logo,
a equação polar do gráfico é r = 4co θ.
O gráfico de x2 + y 2 − 4x = 0 é uma circunferência, podendo ser escrita como
(x − 2)2 + y 2 = 4 que é a equação de uma circunferência com centro em (2, 0)
e raio 2.
Atividades
1) Encontre coordenadas cartesianas retangulares para o ponto cujas coordenadas polares são (−1, π3 ).
2) Escreva a equação x2 + y 2 − 4x − 2y − 4 = 0 = 0 em coordenadas polares.
6.2
Coordenadas Cilíndricas
Vamos definir um outro sistema de coordenadas, chamado de sistema de coordenadas cilíndricas, em que um ponto do espaço é localizado em relação a
duas retas (usualmente, o eixo z e o eixo x do sistema cartesiano) e um ponto
(usualmente a origem O do sistema cartesiano).
No sistema de coordenadas cilíndricas, um ponto no espaço é localizado da
′
seguinte forma: passa-se por P uma reta paralela ao eixo z. Seja P o ponto
em que esta reta intercepta o plano xy. Sejam (r, θ) as coordenadas polares
′
de P no plano xy. As coordenadas cilíndricas do ponto P são as coordenadas
′
polares de P juntamente com a terceira coordenada retangular, z, de P e são
95
escritas na forma (r, θ, z).
Segue facilmente as relações entre as coordenadas cartesianas e as coordenadas
cilíndricas.
Suponha que o polo e o eixo polar do sistema de coordenadas polares no plano
xy coincidem com a origem e o eixo x do sistema de coordenadas cartesianas
no plano xy, respectivamente. Então, a transformação entre os sistemas de
coordenadas cilíndricas e o de coordenadas cartesianas pode ser realizada pelas
equações
x = r cos θ,
y = r sen θ
r=
cos θ = √
x
x2 + y 2
e
√
e
z=z
x2 + y 2 ,
sen θ = √
y
x2 + y 2
, se
√
x2 + y 2 ̸= 0.
Exemplo 6.2.1. Ache uma equação em coordenadas cilíndricas para x2 + y 2 =
z.
Basta substituir x = r cos θ e y = r sen θ, fazendo r2 = x2 + y 2 obtemos:
r2 = z.
96
Ache uma equação em coordenadas cartesianas da superfície cuja equação é
r = sen θ.
Multiplicando-se ambos os membros da equação por r obtemos r2 = r sen θ.
Como r2 = x2 + y 2 e r sen θ = y, então obtemos
x2 + y 2 = y,
que é a equação de um cilindro gerado pela circunferência no plano xy de
equação em coordenadas polares r = sen θ, ou seja, uma circunferência com
raio α/2 e centro no ponto cujas coordenadas cartesianas são (0, α/2).
Atividade
1) Determine uma equação em coordenadas cilíndricas para 3x − 2y + 4z = 1.
6.3
Coordenadas Esféricas
Vamos tratar de outro sistema de coordenadas, chamado de sistema de coordenadas esféricas em que um ponto do espaço é localizado em relação a
duas retas (usualmente o eixo z e o eixo x do sistema cartesiano) e um ponto
(usualmente a origem O do sistema cartesiano). No sistema de coordenadas
esféricas, um ponto no espaço é localizado da seguinte forma: passa-se por P
′
uma reta paralela ao eixo z. Seja P o ponto em que esta reta intercepta o
′
plano xy. Seja θ a segunda coordenada polar de P no plano xy. As coordenadas esféricas do ponto P são a distância de P à origem, ρ = dist(P, O), o
→
−→ −
ângulo, ϕ, entre os vetores OP e k = (0, 0, 1) e a segunda coordenada polar de
97
′
P , θ. As coordenadas esféricas de um ponto P são escritas na forma (ρ, θ, ϕ).
Segue facilmente as relações entre as coordenadas cartesianas e as coordenadas
esféricas.
Suponha que o pólo e o eixo polar do sistema de coordenadas polares no plano
xy coincidem com a origem e o eixo x do sistema de coordenadas cartesianas
no plano xy, respectivamente. Então, a transformação entre os sistemas de
coordenadas esféricas e o de coordenadas cartesianas pode ser realizada pelas
equações
x = ρ sen ϕ cos θ,
ρ=
√
y = ρ sen ϕ sen θ
e
z = ρ cos ϕ
√
x2 + y 2
π
, se z ̸= 0, ϕ = , se z = 0,
z
2
√
y
sen θ = √
, se
x2 + y 2 ̸= 0.
2
x + y2
x2 + y 2 + z 2 , tg ϕ =
cos θ = √
x
x2
+ y2
e
Se o ponto P (ρ, θ, ϕ) não for a origem, então, ρ > 0 e 0 ≤ ϕ ≤ π, em que
ϕ = 0, se P estiver no lado positivo do eixo z e ϕ = π se P estiver no lado
negativo do eixo z.
98
Exemplo 6.3.1. Ache uma equação em coordenadas cartesianas da superfície
cuja equação em coordenadas esféricas é ρ cos ϕ = 4.
Como z = ρ cos ϕ, a equação torna-se z = 4. Logo, o gráfico é um plano
paralelo ao plano xy e 4 unidades acima dele.
Exemplo 6.3.2. Ache uma equação em coordenadas esféricas para 3x + 2y +
6z = 0.
Usando x = ρ sen ϕ cos θ, y = ρ sen ϕ sen θ e z = ρ cos ϕ temos:
3x + 2y + 6z = 0 =⇒ 3ρ sen ϕ cos θ + 2ρ sen ϕ sen θ + 6ρ cos ϕ = 0.
Atividade
1) Determine uma equação em coordenadas esféricas para x2 + y 2 = z.
6.4
Rotação e Translação
Se as coordenadas de um ponto P no espaço são (x, y, z), então, as componentes
−→
do vetor OP também são (x, y, z) e, então, podemos escrever
−→
OP = (x, y, z) = (x, 0, 0) + (0, y, 0) + (0, 0, z)
−
→
→
−
→
−
= x(1, 0, 0) + y(0, 1, 0) + z(0, 0, 1) = x i + y j + z k ,
−
→
−
→
−
→
em que i = (1, 0, 0), j = (0, 1, 0) e k = (0, 0, 1). Ou seja, as coordenadas de um ponto P são iguais aos escalares que aparecem ao escrever−→
mos OP como uma combinação linear dos vetores canônicos. Assim, o ponto
→
−
→ −
→ −
O = (0, 0, 0) e os vetores i , j e k determinam um sistema de coordena→
−
→ −
→ −
das ortogonal, {O, i , j , k }. Para resolver alguns problemas geométricos é
99
necessário usarmos um segundo sistema de coordenadas ortogonal, por
√
′
exemplo, determinado por uma origem O = (2, 3/2, 3/2), U1 = ( 3/2, 1/2, 0),
√
−
→
′
U2 = (−1/2, 3/2, 0) e U3 = (0, 0, 1) = k , então {O , U1 , U2 , U3 } determina
′
um novo sistema de coordenadas: aquele com origem no ponto O , cujos eixos
′
′
′
′
x , y e z são retas que passam por O orientadas com os sentidos e direções
de U1 , U2 e U3 , respectivamente.
′
As coordenadas de um ponto P no sistema de coordenadas {O , U1 , U2 , U3 } são
−−′→
definidas como sendo os escalares que aparecem ao escrevermos O P como combinação linear dos vetores U1 , U2 e U3 , ou seja, se
−−′→
′
′
′
O P = x U1 + y U2 + z U3 ,
100
′
então as coordenadas de P no sistema {O , U1 , U2 , U3 } são dadas por
′
x
′
[P ]{O′ ,U1 ,U2 ,U3 } =
y .
′
z
−→
′
Vamos considerar, inicialmente, o caso em que O = O . Assim, se OP =
−→
′
′
′
(x, y, z), então x U1 + y U2 + z U3 = OP pode ser escrito como
′
[
] x x
′
U1 U2 U3
y = y
′
z
z
[
]
Multiplicando-se à esquerda pela transposta da matriz Q = U1 U2 U3 ,
obtemos
U1t
′
U1t
[
x
] x
′
Ut U U U
y = Ut y
1
2
3
2
2
′
U3t
z
U3t
z
Mas, como U1 , U2 e U3 são unitários e mutuamente ortogonais, então,
t
U1 [
] U1 · U1 U1 · U2 U1 · U3
U · U U · U U · U = I3
t
Qt Q =
=
U
U
U
U
1
2
3
2
2
2
3
2
2 1
U3t
U3 · U1 U3 · U2 U3 · U3
[
]
Assim, a matriz Q = U1 U2 U3 é invertível e Q−1 = Qt . Dessa forma as
coordenadas de um ponto P no espaço em relação ao sistema {O, U1 , U2 , U3 }
′
′
′
estão bem definidas, ou seja, x , y e z estão unicamente determinados e são
dados por
[P ]{O,U1 ,U2 ,U3 }
′
x
x
′
= Qt y = Qt [P ] −
→ .
→−
→−
=
y
{O, i , j , k }
′
z
z
101
Também no plano temos o mesmo tipo de situação que é tratada de forma
inteiramente análoga. As coordenadas de um ponto P no plano em relação a
′
sum sistema de coordenadas {O , U1 , U2 }, em que U1 e U2 são vetores unitários
e ortogonais, é definido como sendo os escalares que aparecem ao escrevermos
−−′→
O P como combinação linear de U1 e U2 , ou seja, se
−−′→
′
′
O P = x U1 + y U2 ,
′
então as coordenadas de P no sistema {O , U1 , U2 } são dadas por
′
x
[P ]{O′ ,U1 ,U2 } =
.
′
y
′
Vamos considerar, também no plano, inicialmente o caso em que O = O .
−→
−→
′
′
Assim, se OP = (x, y), então x U1 + y U2 = OP pode ser escrito como
′
[
]
x x
U1 U2 ′ =
y
y
[
Multiplicando-se à esquerda pela transposta da matriz Q =
mos
U1t
U2t
[
]
U1 U2
′
U1
]
U2 , obte-
U1t
x
x
′ =
.
y
U2t
y
Novamente, como U1 e U2 são unitários e mutuamente ortogonais, então
]
[
t
t
t
U1 U1 U1 U2 U1 · U1 U1 · U2
U1
Qt Q =
= I2
=
U1 U2 =
t
t
t
U2 · U1 U2 · U2
U2 U1 U2 U2
U2
]
[
Assim, a matriz Q =
U1 U2
é invertível e Q−1 = Qt . Desta forma as
coordenadas de um ponto P no plano em relação a um sistema de coordenadas
102
′
′
{O, U1 , U2 } estão bem definidas, ou seja, x e y estão unicamente determinados
e são dados por
′
x
x
[P ]{O,U1 ,U2 } =
= Qt = Qt [P ]{O,E1 ,E2 } ,
′
y
y
em que E1 = (1, 0) e E2 = (0, 1). Observe que, tanto no caso do plano quanto
no caso do espaço, a matriz Q satisfaz, Q−1 = Qt . Uma matriz que satisfaz
esta propriedade é chamada matriz ortogonal.
′
Exemplo 6.4.1. Considere o sistema de coordenadas no plano em que O = O,
√
√
U1 = ( 3/2, 1/2) e U2 = (−1/2, 3/2). Se P = (2, 4), vamos determinar as
coordenadas de P em relação ao novo sistema de coordenadas. Para isto temos
−−′→ −→
′
′
′
′
′ √
que encontrar x e y tais que x U1 + y U2 = O P = OP , ou x ( 3/2, 1/2) +
√
′
y (−1/2, 3/2) = (2, 4).
√
( 3/2)x′ − (1/2)y ′ = 2
A equação acima é equivalente ao sistema linear
√
(1/2)x′ + ( 3/2)y ′ = 4
ou
√
′
′
3/2 −1/2 x 2
x 2
=
ou
ainda,
Q
′ =
√
′
1/2
3/2
y
4
y
4
[
]
em que Q = U1 U2 com U1 e U2 escritos como matrizes colunas. Como
Qt Q =
√
√
3/2 −1/2 3/2 1/2
= I2 ,
√
√
1/2
−1/2
3/2
3/2
então as coordenadas de P , em relação ao novo sistema de coordenadas, são
dadas por
√
2+ 3
2
= √
[P ]{O,U1 ,U2 } = Qt
.
4
2 3−1
103
Exemplo 6.4.2. Considere o mesmo sistema de coordenadas do exemplo anterior, mas, agora, seja P (x, y) um ponto qualquer do plano. Vamos determinar as coordenadas de P , em relação ao novo sistema de coordenadas. Para
−−′→
−→
′
′
′
′
isto temos que encontrar x e y tais que x U1 + y U2 = O P = OP , ou
√
′ √
′
x ( 3/2, 1/2) + y (−1/2, 3/2) = (x, y).
′
′
A equação acima é equivalente ao sistema linear nas variáveis x e y
√
′
′
3/2 −1/2 x x
x x
=
ou
ainda,
Q
=
√
′
′
y
y
y
1/2
3/2
y
[
em que Q =
]
com U1 e U2 escritos como matrizes colunas. Como
U1 U2
Qt Q = I2 , então, as coordenadas de P , em relação ao novo sistema de coordenadas, são dadas por
[P ]{O,U1 ,U2 }
6.4.1
√
x
x ( 3x + y)/2
= Qt =
.
=
√
y
U2t
(−x + 3y)/2
y
U1t
Rotação dos Eixos Coordenados
Suponha que o novo sistema de coordenadas {O, U1 , U2 } seja obtido do sistema
original {O, E1 = (1, 0), E2 = (0, 1)} por uma rotação de um ângulo θ. Observando a figura abaixo, obtemos U1 = (cos θ, sen θ) e U2 = (−sen θ, cos θ). Seja
104
P = (x, y) um ponto qualquer do plano. Vamos determinar as coordenadas de
P , em relação ao novo sistema de coordenadas. Para isso temos que encontrar
′
′
x e y tais que
−→
′
′
x U1 + y U2 = OP .
A equação acima é equivalente ao sistema linear
(cos θ)x′ − (sen θ)y ′ = x
(sen θ)x′ + (cos θ)y ′ = y
ou
Rθ X = P,
cos θ −sen θ
x
em que Rθ =
e P = . A solução é dada por
sen θ
cos θ
y
′
x
cos θ sen θ x
−1
t
= Rθ P = Rθ P =
.
′
y
−sen θ cos θ
y
A matriz Rθ é chamada matriz de rotação.
105
6.4.2
Translação dos Eixos Coordenados
′
Vamos considerar, agora, o caso em que O ̸= O, ou seja, em que ocorre uma
translação dos eixos coordenados.
Observando a figura seguinte, obtemos
−−′→ −→ −−→′
O P = OP − OO .
−−→′
Assim, se OO = (h, k), então
−−′→
′
′
O P = (x , y ) = (x, y) − (h, k) = (x − h, y − k)
Logo, as coordenadas de P , em relação ao novo sistema são dadas por
′
x x−h
[P ]{O,E1 ,E2 } =
=
.
′
y
y−k
′
′
′
′
O eixo x tem equação y = 0, ou seja, y = k e o eixo y , x = 0, ou seja,
x = h.
106
Atividades
1) Ache (r, θ), se r > 0 e 0 ≤ θ ≤ 2π para o ponto cuja representação cartesiana
√
é (− 3, −1).
2) Ache a equação polar do gráfico cuja equação cartesiana é x2 = 6y − y 2 .
3) Encontre uma equação em coordenadas cilíndricas da superfície de equação
x2 + y 2 + 4z 2 = 16.
4) Encontre uma equação em coordenadas esféricas da superfície de equação
x2 + y 2 + z 2 − 8x = 0.
5) Encontre o ponto P , se as coordenadas de P em relação ao sistema de
coordenadas S, P[S] são:
P[S]
−1
√
√
√
√
, em que S = {O, (0, 1/ 2, −1/ 2), (1, 0, 0), (0, 1/ 2, 1/ 2)}
=
1
2
6) Determine
quala rotação do plano em que as coordenadas do ponto P =
√
√
3
( 3, 1) são
.
−1
107
capítulo
Cônicas
Objetivos
• Reconhecer a equação de uma elipse, de uma hipérbole e de uma parábola e
seus elementos;
• Determinar a equação de uma elipse, de uma hipérbole e de uma parábola
em diferentes situações;
109
7
7.1
Introdução
Você já ouviu falar de certas curvas chamadas elipse, parábola e hipérbole? O
objetivo deste capítulo é buscarmos uma compreensão dessas curvas do ponto
de vista da geometria analítica.
Imagine duas retas que não são perpendiculares e que se interceptam no ponto
V . Se fixarmos uma das retas como eixo e fizermos uma rotação com a outra ao
redor desse eixo, obtemos um sólido denominado cone circular reto com vértice
V , como ilustrado abaixo. Note que o ponto V divide o cone em duas partes,
chamadas folhas.
Mas, você deve estar se perguntando, qual é a relação que existe entre esse tal
cone circular reto e as curvas citadas? O fato é que a elipse, a hipérbole e a
parábola são originadas a partir desse tal cone. Com isso, podemos definir uma
secção cônica ( ou simplesmente cônica) sendo a intersecção de um plano com
um cone circular reto. As três secções cônicas básicas são a parábola, a elipse
e a hipérbole.
111
Percebeu o aspecto geométrico dessas curvas? Pois bem! Vamos conhecer um
breve histórico das cônicas. Historicamente, o matemático grego, Pappus de
Alexandria (290 − 350), atribuiu ao geômetra grego, Aristeu (o Ancião) (370 −
300) a.C., o crédito de ter publicado o primeiro tratado sobre as seções cônicas,
referindo-se aos Cinco livros sobre seções cônicas de Aristeu, nos quais foi
apresentado um estudo cuidadoso das curvas cônicas e as suas propriedades.
Segundo Pappus, o matemático grego, Euclides de Alexandria (325 − 265) a.C.,
contemporâneo de Aristeu, conhecia muito bem os cinco livros sobre as curvas
cônicas e evitou aprofundar-se sobre esse assunto na sua obra, Os elementos, de
modo a obrigar os leitores interessados a consultar a obra original de Aristeu.
Duzentos anos mais tarde, o astrônomo e matemático grego, Apolônio de Perga
(262 − 190)a.C., recompilou e aprimorou os resultados de Aristeu e de Euclides
nos oito livros da sua obra Seções Cônicas. No entanto, a História indica que as
cônicas foram descobertas pelo matemático grego, Menaecmus (380 − 320) a.C.
aproximadamente quando estudava como resolver os três problemas famosos da
Geometria grega: a trisseção do ângulo, a duplicação do cubo e a quadratura do
círculo. Segundo o historiador Proclus, Menaecmus nasceu em Alopeconnesus,
na Ásia Menor (o que hoje é a Turquia), foi aluno de Eudóxio na academia de
112
Platão.
Menaecmus foi o primeiro em mostrar que as elipses, parábolas e hipérrboles
são obtidas cortando um cone com um plano não paralelo a sua base. Mesmo
assim, pensava-se que os nomes dessas curvas foram inventados por Apolônio,
porém traduções de antigos escritos árabes indicam a existência desses nomes
em épocas anteriores a Apolônio.
Gostou da história? Vamos, então, inicar nossa tarefa de compreendermos as
cônicas do ponto de vista da geometria analítica.
7.2
Elipse
O jardineiro, senhor Antônio, cuidava do jardim da praça com muito carinho.
Certo dia, quando fazia a manutenção semanal do jardim, resolveu fazer uma
curva no gramado de modo a plantar rosas na região delimitada por essa curva.
O senhor Antônio construiu a curva da seguinte forma: Fincou duas estacas no
terreno e amarrou nelas as extremidades de uma corda maior do que a distância
entre as estacas. Assim, desenhou a curva no solo com o auxílio de um graveto
apoiado na corda, mantendo-a o mais esticada possível.
113
Essa curva , que o senhor Antônio construiu com tanto carinho, é denominada
elípse. Apresentaremos, agora, a definição precisa e formal da elipse.
Definição 7.2.1. Uma elipse, E, de focos F1 e F2 , é o conjunto de pontos P
de um plano, cuja soma das distâncias a F1 e F2 é igual a uma constante, que
será denotada por 2a > 0, maior do que a distância entre os focos 2c, ou seja
E = {P ; dist(P, F1 ) + dist(P, F2 ) = 2a > dist(F1 , F2 ) = 2c}
Você deve ter notado que, a definição anterior representa a elaboração matemática da curva que o senhor Antônio construiu em seu jardim.
Observe que, comparando a definição dada com a curva que o senhor Antônio
construiu, as estacas representam os focos da elipse. Isso sugere descrevermos
os elementos notáveis de uma elipse.
Terminologia:
• Como dissemos na definição, os pontos F1 e F2 são os focos da elipse.
• A reta que contém os focos é a reta focal, que será denotada por l;
• A intersecção da elipse com a reta focal l consiste de exatamente dois pontos
114
A1 e A2 , chamados vértices da elipse sobre a reta focal.
• O segmento A1 A2 é denominado eixo focal da elipse. O seu comprimento é
2a.
• O ponto médio C do eixo focal A1 A2 é o centro da elipse. Esse ponto é,
também, o ponto médio do segmento F1 F2 , delimitado pelos focos.
′
• A reta l que passa pelo centro C e é perpendicular a reta focal é a reta não
focal.
′
• A elipse intercepta a reta não focal l em exatamente dois pontos, B1 e B2 ,
denominados vértices da elipse sobre a reta não focal.
• O segmento B1 B2 é denominado eixo não focal da elipse e seu comprimento
é 2b, em que b2 = a2 − c2 .
• O número a é a distância do centro aos vértices sobre a reta focal, b é a
distância do centro aos vértices sobre a reta não focal e c é distância do
centro aos focos.
• O número e =
c
é chamado excentricidade da elipse. Note que 0 ≤ e < 1.
a
Antes de prosseguirmos, o que significa, de fato, a excentricidade de uma
elipse? Você tem alguma ideia? A excentricidade é uma medida que mostra
o quanto os pontos da elipse estão próximos de uma circunferência ou de um
segmento de reta. Fixada a medida 2a do eixo focal, tem-se que: quanto mais
próximos estiverem os focos, mais próximos de uma circunferência estarão os
pontos da elipse e, quanto mais distintas estiverem os focos, mais próximos
de um segmento de reta estarão os pontos da elipse.
115
Assim, quanto mais próximo de zero estiver o número e = ac , mais próximos
de uma circunferência estarão os pontos da elipse, e, quanto mais próximo
de 1 estiver o número e, mais próximos de um segmento de reta estarão os
pontos da elipse.
Caso c = 0, a elipse se reduz a uma circunferência de centro em C e raio a,
pois, nesse caso, F1 = F2 = C e, portanto,
E = {P ; dist(P, C) = a}
Em particular, e = 0, se, e somente se, a elipse é uma circunferência.
7.2.1
Equação da Elipse com Centro na Origem do Sis-
tema
Quando você se depara com a expressão equação da elipse, o que lhe vem à
mente? Pense no significado dessa expressão. Com isso, vamos considerar
xOy um sistema de eixos ortogonais no plano. Nosso objetivo é obter a equação da elipse em relação a esse sistema de eixos para alguns casos especiais.
Proposição 7.2.1. A elipse de focos, nos pontos F1 = (−c, 0) e F2 = (c, 0)
e vértices em A1 = (−a, 0), A2 = (a, 0), B1 = (0, −b) e B2 = (0, b), tem por
equação
x2 y 2
+ 2 =1
a2
b
Demonstração. Seja E a elipse mencionada, e P um ponto de E. Então, usando
116
a definição de elipse, temos:
P ∈ E ⇐⇒ dist(P, F1 ) + dist(P, F2 ) = 2a
e, agora, utilizando a distância entre dois pontos, segue que
√
(x + c)2 + y 2 +
√
(x − c)2 + y 2 = 2a
o que equivale escrever que
√
(x + c)2 + y 2 = 4a2 − 4a (x − c)2 + y 2 + (x − c)2 + y 2
e, após simplificar
√
4xc = 4a2 − 4a (x − c)2 + y 2
logo, temos que
(a2 − cx)2 = a2 ((x − c)2 + y 2 )
de onde concluimos que
b2 x2 + a2 y 2 = a2 b2 ⇐⇒
117
x2 y 2
+ 2 =1
a2
b
E, então, você já tem em mente o significado da equação de uma elipse? Essa
reflexão é de fundamental importância antes de prosseguir.
Proposição 7.2.2. A elipse de focos nos pontos F1 = (0, −c) e F2 = (0, c)
e vértices em A1 = (0, −a), A2 = (0, a), B1 = (−b, 0) e B2 = (b, 0) tem por
equação
x2 y 2
+ 2 =1
b2
a
Demonstração. Análoga à anterior.
Exemplo 7.2.1. Os focos de uma elipse são os pontos (2, 0) e (−2, 0) e sua
2
excentricidade é igual a . Determinar a equação da elipse.
3
Temos que a reta focal é o eixo das abscissas, o centro da elipse é a origem
2
c
C(0, 0) , c = 2 e e = = =⇒ a = 3.
3
a
118
Logo, b2 = a2 − c2 = 9 − 4 = 5
Portanto a equação da elipse é
x2 y 2
+
=1
9
5
Exemplo 7.2.2. Uma elipse tem seu centro na origem e um de seus vértices
√ 14
sobre a reta focal é (0, 7). Se a elipse passa pelo ponto ( 5, ), determinar
3
sua equação.
A reta focal, que contém o centro e o vértice dados, é o eixo das ordenadas. A
distância do centro C(0, 0) ao vértice A2 = (0, 7) é a = 7, e o outro vértice na
reta focal é A1 (0, −7).
Logo, a equação da elipse é da forma
x2 y 2
+ 2 =1
b2
7
√ 14
Como ( 5, ) ∈ E, temos que
3
√
5
b2
+
14
3
49
= 1 =⇒
5
4
=
1
−
=⇒ b2 = 9
b2
9
Assim, a equação da elipse é
x2 y 2
+
=1
9
49
Antes de prosseguirmos, vamos questionar o seguinte: Como obter as equações
descritas anteriormente, caso as elipses não possuíssem centro na origem do
sistema?
Poderíamos proceder da mesma forma, porém teríamos muito mais trabalho
para alcançarmos as equações desejadas. Você se lembra da translação de eixos
119
que estudamos anteriormente? Pois bem, faremos uso da translação de eixos
para obtermos as equações de uma elipse com centro em um ponto qualquer.
7.2.2
′
Equação da Elipse com Centro no Ponto O (x0 , y0 )
Usando a translação de eixos, vamos estudar agora as equações de uma elipse
com centro fora da origem.
′
Proposição 7.2.3. A equação da elipse com centro no ponto O (x0 , y0 ) e eixo
focal paralelo ao eixo ox é
(x − x0 )2 (y − y0 )2
+
=1
a2
b2
′
Demonstração. Como o centro O (x0 , y0 ) pertence à reta focal, temos que
y = y0 é a equação cartesiana da reta focal.
′
′
Além disso, como dist(F1 , O ) = dist(F2 , O ) = c, em que F1 e F2 são os focos
da elipse, temos que F1 = (x0 − c, y0 ) e F2 = (x0 + c, y0 ).
′
′
Seja um ponto P (x + x0 , y + y0 ) pertencente à elipse, em que x e y são suas
′
′
′
′
′
coordenadas no sistema xoy e x e y são suas coordenadas no sistema x O y ,
obtido transladando o sistema xOy para a origem (x0 , y0 ).
Então,
P ∈ E ⇐⇒ dist(P, F1 ) + dist(P, F2 ) = 2a
120
ou seja,
′
′
′
′
dist((x + x0 , y + y0 ), (x0 − c, y0 )) + dist((x + x0 , y + y0 ), (x0 + c, y0 )) = 2a
o que equivale escrever que
′
′
′
′
dist((x , y ), (−c, 0)) + dist((x , y ), (c, 0)) = 2a
portanto
′
′
(x )2 (y )2
(x − x0 )2 (y − y0 )2
+
=
1
⇐⇒
+
=1
a2
b2
a2
b2
′
Proposição 7.2.4. A equação da elipse com centro no ponto O (x0 , y0 ) e eixo
focal paralelo ao eixo oy é
(x − x0 )2 (y − y0 )2
+
=1
b2
a2
121
Demonstração. Análoga ao caso anterior.
Exemplo 7.2.3. Determine o centro, os vértices, os focos e a excentricidade
da elipse de equação
4x2 + 9y 2 − 8x − 36y + 4 = 0
Para que a equação possa ser analisada, devemos colocá-la na forma
(x − x0 )2 (y − y0 )2
+
=1
a2
b2
Primeiramente, vamos agrupar os termos de mesma variável
(4x2 − 8x) + (9y 2 − 36y) = −4
ou
4(x2 − 2x) + 9(y 2 − 4y) = −4
onde colocamos em evidência os números 4 e 9 para facilitar a construção de
trinômios quadrados nestes dois parênteses.
4(x2 − 2x + 1) + 9(y 2 − 4y + 4) = −4 + 4(1) + 9(4)
122
ou
4(x − 1)2 + 9(y − 2)2 = 36
Dividindo ambos os membros da equação anterior por 36 obtemos
(x − 1)2 (y − 2)2
+
=1
9
4
Agora, comparando esta última equação com a equação padrão, temos que
O centro da elípse é o ponto C(1, 2).
mas
a2 = 9 =⇒ a = 3
b2 = 4 =⇒ b = 2
Logo, os vértices são dados por
A1 (−2, 2), A2 (4, 2), B1 (1, 0), B2 (1, 4)
Para determinarmos os focos, precisamos do valor de c:
123
9 = 4 + c2 =⇒ c =
√
5
Portanto, os focos são :
F1 (1 −
√
5, 2), F2 (1 +
√
5, 2)
e a excentricidade é dada por
√
c
5
e= =
.
a
3
Atividades
1) Determine os vértices A1 e A2 , os focos e a excentricidade das elipses dadas.
x2
y2
a)
+
=1
144 81
x2
y2
b)
+
=1
25 100
c) x2 + 25y 2 = 25
d) 9x2 + 5y 2 − 45 = 0
e) 4x2 + y 2 = 1
2) Apresente a equação da elipse que satisfaz as condições dadas:
a) Centro C(0, 0), um foco F ( 34 , 0) e um vértice A(1, 0)
124
b) vértices A(0, ±6) e passando por P (3, 2)
c) vértices A1 (1, −4) e A2 (1, 8) e excentricidade e = 32 .
d) centro C(2, 1), tangente aos eixos coordenados e eixos de simetria paralelos
aos eixos coordenados.
e) centro C(2, 4), um foco F (5, 4) e excentricidade e = 43 .
3) Determine o centro, os focos e a excentricidade de cada elipse a seguir:
a)
(x − 2)2 (y + 3)2
+
=1
16
9
b) 25x2 + 16y 2 + 50x + 64y − 311 = 0
c) 4x2 + 9y 2 − 24x + 18y + 9 = 0
d) 4x2 + 9y 2 − 8x − 36y + 4 = 0
e) 16x2 + 9y 2 − 96x + 72y + 144 = 0
125
7.3
Hipérbole
Definição 7.3.1. Uma hipérbole, H,de focos F1 e F2 , é o conjunto de pontos
P de um plano tais que o módulo da diferença das distâncias a F1 e a F2 é
igual a uma constante 2a > 0, menor do que a distância entre os focos.
H = {P ; | dist(P, F1 ) − dist(P, F2 ) |= 2a < dist(F1 , F2 )}
Terminologia:
• Os pontos F1 e F2 são os focos da hipérbole;
• A reta l que contém os focos é a reta focal.
• A intersecção da hipérbole com a reta focal l consiste de exatamente dois
pontos A1 e A2 , chamados de vértices da hipérbole.
• O segmento A1 A2 é denominado eixo focal da hipérbole e seu comprimento é
dist(A1 A2 ) = 2a.
• O ponto médio C do eixo focal A1 A2 é o centro da hipérbole. Esse ponto é,
também, o ponto médio do segmento F1 F2 , delimitado pelos focos.
′
• A reta l que passa pelo centro C e é perpendicular a reta focal é a reta não
126
′
focal da hipérbole. Como l é a mediatriz do segmento F1 F2 , a hipérbole não
′
′
interce a reta não focal l , pois se P ∈ l , temos
| dist(P, F1 ) − dist(P, F2 ) |= 0 ̸= 2a
• O segmento B1 B2 perpendicular ao eixo focal que tem C como ponto médio
e comprimento 2b, em que b2 = c2 − a2 , é denominado eixo não focal da
hipérbole, e B1 e B2 são os vértices imaginários da hipérbole.
c
é denominado a excentricidade da hipérbole. Note que
a
e > 1, pois c > a.
• O número e =
A excentricidade é uma medida que mostra o quanto os pontos da hipérbole
se aproximam de duas retas que passam pelos seus vértices paralelamente ao
eixo não focal ou o quanto esses pontos se aproximam da reta que contém
o eixo focal. Quanto maior o número e = ac , mais próximos de duas retas
paralelas estarão os pontos da hipérbole; quanto menor o número e = ac , mais
próximos da reta que contém o eixo focal estarão os pontos da hipérbole.
• O retângulo de base da hipérbole H é o retângulo que tem os pontos A1 , A2 ,
B1 e B2 como pontos médios de seus lados e as retas que contém as diagonais
de retângulo de base da hipérbole H são as assíntotas de H.
Portanto as assíntotas da hipérbole H são as retas que passam pelo centro da
hípérbole e tem coeficinte angular ± ab em relação a reta focal.
127
Pelo teorema de Pitágoras, as diagonais do retângulo de base de H tem comprimento 2c e a distância do centro de H a qualquer vértice do retângulo de
base é igual a c.
• Uma hipérbole é denominada equilátera, se o comprimento do eixo focal é
igual ao comprimento do eixo não focal, isto é, a = b.
• Duas hipérboles tais que o eixo focal de cada uma é igual ao eixo não focal da
outra são denominadas hipérboles conjugadas. Como os retângulos de base
de duas hipérboles conjugadas são iguais, elas tem o mesmo centro, mesmas
assíntotas e os focos de uma mesma distância do centro.
7.3.1
Equação da Hipérbole com Centro na Origem
Proposição 7.3.1. A equação da hipérbole com centro na origem e reta focal
coincidente com o eixo das abscissas é dada por
x2 y 2
− 2 =1
a2
b
Demonstração. Neste caso, temos F1 (−c, 0), F2 (c, 0), A1 (−a, 0), A2 (a, 0), B1 (0, −b),
B2 (0, b) e C(0, 0). Logo,
P (x, y) ∈ H ⇐⇒| dist(P, F1 ) − dist(P, F2 ) |= 2a
mas
| dist(P, F1 ) − dist(P, F2 ) |=
√
128
(x + c)2 + y 2 −
√
(x − c)2 + y 2 = ±2a
Continuando o desenvolvimento de maneira análoga ao caso da elípse, e lembrando que b2 = c2 − a2 , chegamos a
P (x, y) ∈ H ⇐⇒ (c2 − a2 )x2 − a2 y 2 = a2 (c2 − a2 ) ⇐⇒ b2 x2 − a2 y 2 = a2 b2
Dividindo ambos os membros da última igualdade por a2 b2 temos que
x2 y 2
− 2 =1
a2
b
Proposição 7.3.2. A equação da hipérbole de centro na origem e reta focal
coincidente com o eixo das ordenadas é dada por
y 2 x2
− 2 =1
a2
b
Demonstração. Neste caso, temos F1 (0, −c), F2 (0, c), A1 (0, −a), A2 (0, a), B1 (−b, 0)
e B2 (b, 0).
Procendendo como no caso anterior, obtemos a equação da hipérbole.
Exemplo 7.3.1. Considere a hipérbole 9x2 − 7y 2 − 63 = 0. Determinar as
coordenadas de seus focos e sua excentricidade.
Observe que a equação dada pode ser escrita da seguinte forma
129
x2 y 2
−
= 1.
7
9
Agora,
a2 = 7 =⇒ a =
√
7
b2 = 9 =⇒ b = 3
e, para determinarmos os focos, precisamos do valor de c:
c2 = 7 + 9 =⇒ c = 4
Logo, os focos são F1 (−4, 0) e F2 (4, 0).
A excentricidade da hipérbole é dada por
e=
130
c
4
=√
a
7
Exemplo 7.3.2. Determine a equação da hipérbole equilátera com focos nos
√
√
pontos (− 8, 0) e ( 8, 0).
√
√
F1 + F2
Como F1 (− 8, 0) e F2 ( 8, 0), temos que o centro da hipérbole é C =
=
2
(0, 0) e a reta focal é o eixo das abscissas. Sendo a hipérbole equilátera, temos
√
que a = b. Como c = 8 e c2 = a2 + b2 , obtemos 8 = a2 + a2 = 2a2 , isto é,
a2 = 4. Logo, a = b = 2 e
H:
x2 y 2
−
=1
4
4
é a equação da hipérbole.
Exemplo 7.3.3. Mostre que a excentricidade de qualquer hipérbole equilátera
√
é 2.
Como a = b e c2 = a2 + b2 temos que c2 = 2a2 , ou seja, c =
√
√
e = ac = a2a = 2.
√
2a. Logo,
Exemplo 7.3.4. Os vértices de uma hipérbole são os pontos (0, 3) e (0, −3)e,
um de seus focos é o ponto (0, 5). Determine a equação da hipérbole, o comprimento do seu eixo focal e suas assíntotas.
A hipérbole tem centro C(0, 0); reta focal dada por x = 0; c = 5, a = 3 e o
ponto (0, −5) representa as coordenadas do outro foco. Com isso, temos que,
b2 = c2 − a2 = 16.
y 2 x2
−
= 1 é a equação da hipérbole, y = ± 4y
são suas assíntotas
3
9
16
e 2a = 6 é o comprimento do seu eixo focal.
Então, H :
131
′
7.3.2
Equação da Hipérbole com Centro no Ponto O (x0 , y0 )
Proposição 7.3.3. A equação da hipérbole com centro no ponto (x0 , y0 ) e reta
focal paralela ao eixo das abscissas é dada por
(x − x0 )2 (y − y0 )2
−
=1
a2
b2
′
Demonstração. Como o centro O (x0 , y0 ) pertence a reta focal, temos que
l : y = y0 é a equação cartesiana da reta focal.
Além disso, como
′
′
dist(F1 , O ) = dist(F2 , O ) = c
onde F1 e F2 são os focos da elípse, temos que F1 (x0 − c, y0 ) e F2 (x0 + c, y0 ).
′
′
Seja P (x + x0 , y + y0 ) um ponto pertencente a hipérbole, onde
′
′
x = x + x0
y = y + y0
′
′
são suas coordenadas no sistema xOy e x e y são suas coordenadas no sistema
′
′
′
′
x O y , obtido transladando o sistema xOy para a origem O (x0 , y0 ).
Então,
P ∈ H ⇐⇒| dist(P, F1 ) − dist(P, F2 ) |= 2a
132
ou seja
′
′
′
′
| dist((x + x0 , y + y0 ), (x0 − c, y0 )) − dist((x + x0 , y + y0 ), (x0 + c, y0 )) |= 2a
que é equivalente a
′
′
′
′
| dist((x , y ), (−c, 0)) − dist((x , y ), (c, 0)) |= 2a
Logo, temos
′
′
(x )2 (y )2
(x − x0 )2 (y − y0 )2
− 2 = 1 ⇐⇒
−
=1
a2
b
a2
b2
Proposição 7.3.4. A equação da hipérbole com centro no ponto (x0 , y0 ) e reta
focal paralela ao eixo das ordenadas é dada por
133
(y − y0 )2 (x − x0 )2
−
=1
a2
b2
Demonstração. Análoga ao caso anterior.
Exemplo 7.3.5. A equação x2 −2y 2 +6x+4y +9 = 0 representa uma hipérbole.
Apresentar seus elementos principais.
Separando os termos de mesma variável e completando os quadrados, obtemos:
(y − 1)2 −
(x + 3)2
=1
2
Logo, a equação representa uma hipérbole com:
• a = 1, b =
√
2ec=
√
a2 + b 2 =
√
1+2=
√
3.
• centro: C(−3, 1).
• reta focal: l : x = −3 paralela ao eixo das ordenadas.
′
• reta não focal: l : y = 1 paralela ao eixo das abscissas.
• vértices: A1 (−3, 0) e A2 (−3, 2).
√
√
• vétices imaginários ( na reta não focal): B1 (−3 − 2, 1) e B2 (−3 + 2, 1)
√
√
• focos: F1 (−3, 1 − 3, ) e F2 (−3, 1 + 3).
√
√
√
√
• assíntotas: (x + 3) = ± 2(y − 1), ou seja, x + 2y = −3 + 2 e x − 2y =
√
−3 − 2.
134
Exemplo 7.3.6. Mostre que as assíntotas de uma hipérbole não se intersectam.
Podemos supor, sem perda de generalidade ( escolhendo o sistema de coordenadas de maneira adequada), que a hipérbole é dada pela equação
x2 y 2
H: 2 − 2 =1
a
b
ou seja, H : b2 x2 − a2 y 2 = a2 b2 .
Como r+ : bx − ay = 0 e r− : bx + ay = 0 são as assíntotas da hipérbole e
H : (bx − ay)(bx + ay) = a2 b2
,
temos que r+ ∩ H = ∅ e r− ∩ H = ∅, pois (bx − ay)(bx + ay) = 0 ̸= a2 b2 se
(x, y) ∈ r+ ∪ r− .
Atividades
1) As equações a seguir representam hipérboles. Para cada uma delas, determine os vértices, os focos e a excentricidade.
x2
y2
−
=1
100 64
y2
x2
b)
−
=1
100 64
a)
c) 9x2 − 16y 2 = 144
d) x2 − 2y 2 − 8 = 0
135
e) x2 − 4y 2 − 18x − 16y − 43 = 0
2) Determinar a equação da hipérbole que satisfaz as condições dadas:
a) focos F (±5, 0), vértices A(±3, 0).
b) vértices em (5, −2) e (3, −2), um foco em (7, −2).
c) focos em (3, 4) e (3, −2), excentricidade e = 2.
d) centro C(−2, 1), eixo focal paralelo ao eixo das abscissas, passando por (0, 2)
e (−5, 6)
e) vértices A(±3, 0), equações das assíntotas y = ±2x.
136
7.4
Parábola
Com uma mangueira de água, dirija o jato obliquamente para cima e observe a
trajetória percorrida pela água. Essa trajetória é parte de uma curva denominada parábola. Pense outras situações reais que você acredita ser uma parábola
e depois compare suas situações com a definição formal dessa curva que é dada
se seguir.
Definição 7.4.1. Seja L uma reta no plano e F um ponto no plano não pertencente a L. A parábola P de diretriz L e foco F é o conjunto que consiste de
todos os pontos P do plano que são equidistantes do ponto F e da reta L, ou
seja
P = {P ; dist(P, F ) = dist(P, L)}
Terminologia
• Como apresentamos na definição, o ponto F é o foco e a reta L é chamada
diretriz da parábola.
• A reta l que contém o foco e é perpendicular à diretriz L é chamada reta
focal da parábola.
• O vértice da parábola é o ponto V da reta focal que equidista de F e de L.
• Se A é o ponto em que L intersecta l, então, V é o ponto médio do segmento
AF , ou seja,
V =
137
A+F
2
• O número dist(P, L) = 2p é o parâmetro da parábola. Note que dist(V, F ) =
dist(V, L) = p.
7.4.1
Equação da Parábola com Vértice na Origem
Vamos estabelecer as equações da parábola em relação a um sistema de coordenadas xOy no plano. Consideremos, primeiro, os casos em que o vértice da
parábola é a origem, e a reta focal é um dos eixos coordenados, e, depois, os
casos em que o vértice é um ponto qualquer, e a reta focal é paralela a um dos
eixos coordenados.
Proposição 7.4.1. A equação da parábola com vértice na origem, reta focal
coincidente com o eixo das abscissas e foco à direita da diretriz é dada por
y 2 = 4px
Demonstração. Como o vértice da parábola P é V (0, 0), temos que o foco é
F (p, 0) e a diretriz é L : x = −p onde 2p = dist(F, L).
Logo,
138
P (x, y) ∈ P ⇐⇒ dist(P, F ) = dist(P, L)
Da última igualdade segue que
√
(x − p)2 + y 2 =| x + p |
que é o mesmo que escrever
(x − p)2 + y 2 = (x + p)2
e com isso temos
y 2 = 4px
Proposição 7.4.2. A equação da parábola com vértice na origem, reta focal
coincidente com o eixo das abscissas e foco à esquerda da diretriz é dada por
y 2 = −4px
Demonstração. Neste caso, temos F (−p, 0) e L : x = p, em que 2p = dist(F, L).
Então,
P (x, y) ∈ P ⇐⇒ dist(P, F ) = dist(P, L)
Da última igualdade segue que
139
√
(x + p)2 + y 2 =| x − p |
que é o mesmo que escrever
(x + p)2 + y 2 = (x − p)2
e com isso temos
y 2 = −4px
Proposição 7.4.3. A equação da parábola com vértice na origem, reta focal
coincidente com o eixo das ordenadas e foco acima da reta diretriz é dada por
x2 = 4py
Demonstração. Neste caso, F (0, p) e L : y = −p, onde dist(F, L) = 2p.
Logo,
140
P (x, y) ∈ P ⇐⇒ dist(P, F ) = dist(P, L) ⇐⇒
√
x2 + (y − p)2 ⇐⇒ x2 = 4py
Proposição 7.4.4. A equação da parábola com vértice na origem, reta focal
coincidente com o eixo das ordenadas e foco abaixo da diretriz é dada por
x2 = −4py
Demonstração. Neste caso, F (0, −p) e L : y = p, onde dist(F, L) = 2p.
Logo,
P (x, y) ∈ P ⇐⇒ dist(P, F ) = dist(P, L) ⇐⇒
√
x2 + (y + p)2 ⇐⇒ x2 = −4py
Exemplo 7.4.1. Determinar os elementos principais da parábola x2 − 8y = 0.
Como x2 = 8y, a equação representa uma parábola com
• vértice: V (0, 0);
• reta focal: eixo Oy: x = 0;
• parâmetro: p = 2;
• foco: F (0, 2); acima da diretriz;
• diretriz: y = −2.
141
Exemplo 7.4.2. Considere uma parábola P com vértice na origem, cuja reta
focal é o eixo Oy e que passa pelo ponto (4, −2). Determine sua equação, o
foco F e a equação de sua diretriz L.
A parábola tem equação x2 = ±4py, com p = dist(V, P ) > 0.
Como (4, −2) ∈ P, temos que P : x2 = −4py e 16 = 8p. Logo, p = 2; F (0, −2),
L : y = 2 e a equação da parábola é P : x2 = −8y.
7.4.2
Parábola com Vértice no Ponto V (x0 , y0 )
Proposição 7.4.5. A equação da parábola com vértice no ponto V (x0 , y0 ), reta
focal paralela ao eixo das abscissas e foco a direita da diretriz é dada por
(y − y0 )2 = 4p(x − x0 )
Demonstração. Sabemos que a equação da parábola no sistema de coordena′
′
′
′
′
das x O y é dada por (y )2 = 4px . Além disso, nesse sistema de coordenadas,
′
o foco é F (p, 0), o vértice V (0, 0) , a diretriz é L : x = −p e a reta focal é
′
l : y = 0.
′
′
Como x = x + x0 e y = y + y0 , temos que a equação da parábola no sistema
xOy é (y − y0 )2 = 4p(x − x0 ).
Proposição 7.4.6. A equação da parábola com vértice na origem, reta focal
paralela ao eixo das abscissas e foco a esquerda da diretriz é dada por
142
(y − y0 )2 = −4p(x − x0 )
Demonstração. Análoga ao caso anterior.
′
′
Como nos casos anteriores, considerando um sistema de eixos ortogonais x O y
′
′
′
′
′
′
com origem O = V (x0 , y0 ) e eixos O x e O y paralelos e de igual sentido
aos eixos Ox e Oy, respectivamente, obtemos as equações e os elemntos das
parábolas com vértice V (x0 , y0 ) e reta focal paralela ao eixo das ordenadas.
Proposição 7.4.7. A equação da parábola com vértice V (x0 , y0 ), reta focal
paralela ao eixo das ordenadas e foco acima da diretriz é dada por
(x − x0 )2 = 4p(y − y0 )
Demonstração. Basta considerar F (x0 , y0 + p), diretriz L : y = y0 − p e usar a
definição de parábola.
143
Proposição 7.4.8. A equação da parábola com vértice no ponto V (x0 , y0 ), reta
focal paralela ao eixo das ordenadas e foco abaixo da diretriz é dada por
(x − x0 )2 = −4p(y − y0 )
Demonstração. Basta considerar F (x0 , y0 − p), diretriz L : y = y0 + p e usar a
definição de parábola.
Exemplo 7.4.3. Considere a parábola 2y 2 + 5x + 8y − 7 = 0. Determine seus
elementos principais.
A equação dada pode ser escrita da seguinte forma
2(y 2 + 4y) = −5x + 7
Após completar o quadrado, obtemos
2(y + 2)2 = −5x + 15
logo
(y + 2)2 =
representa uma parábola com:
• vértice: V (3, −2);
• reta focal: l = y = −2;
• parâmetro: 2p =
10
5
, então, p = ;
8
8
144
−5
(x − 3)
2
5
19
• foco: (3 − , −2) = ( , −2) à esquerda da diretriz;
8
8
5
29
• diretriz: L : x = 3 + =
8
8
Exemplo 7.4.4. Determine a equação da parábola P de vértice V (3, 4) e foco
F (3, 2). Determine, também, a equação de sua diretriz.
Como V (3, 4) e F (3, 2), a reta focal é l : x = 3 e, nessa reta, F está abaixo de
V e, portanto, abaixo da diretriz L. Logo, a equação da parábola é da forma
P : (x − 3)2 = −4p(y − 4)
Temos que p = dist(V, F ) = dist((3, 4), (3, 2)) = 2. Logo a diretriz é L : y = 6
e
P : (x − 3)2 = −8(y − 4)
é a equação da parábola.
Atividades
1) Determine os elementos principais de cada parábola a seguir:
a) x2 = −12y
b) y 2 = −100x
c) x2 + 4x + 8y + 12 = 0
d) y 2 + 4y + 16x − 44 = 0
e) y 2 + 2y − 16x − 31 = 0
145
2) Estabeleça a equação de cada uma das parábolas sabendo que:
a) vértice: V (0, 0) e diretriz y = −2
b) foco: F (2, 0) e diretriz x + 2 = 0
c) vértice: V (−4, 3) e foco F (−4, 1)
d) foco F (6, 4) e diretriz y = −2
e) foco F (3, −1) e diretriz x =
1
2
146
capítulo
8
Superfícies Quádricas
Objetivo
• Reconhecer superfícies quádricas, superfícies cônicas e superfícies cilíndricas.
147
8.1
Introdução
Pelo nome genérico de quádrica, vamos designar algumas superfícies do espaço
que podem ser consideradas, por assim dizer, a versão tridimensional das cônicas. Veremos, no decorrer de nossa conversa, que tais superfícies podem ser
encontradas no mundo a nossa volta.
Definição 8.1.1. Uma quádrica é uma superfície cuja equação cartesiana é
uma equação de segundo grau, nas variáveis x, y e z, isto é, uma equação da
forma
ax2 + by 2 + cz 2 + 2dxy + 2exz + 2f yz + mx + ny + pz + q = 0
em que pelo menos um dos coeficientes a, b, c, d, e ou f , é diferente de zero.
Observemos que, se a superfície quádrica, dada na definição anterior, for cortada pelos planos coordenados ou por planos paralelos a eles, a curva de intersecção será uma cônica. A intersecção de uma superfície com um plano é
chamada traço da superfície no plano.
Por exemplo, o traço da superfície da definição no plano z = 0 é a cônica
ax2 + by 2 + 2dxy + mx + ny + q = 0
contida no plano z = 0, isto é, no plano xOy.
Estaremos interessados em estudar alguns casos particulares que a equação dada
na definição acima assume, por meio de translação e rotação.
149
8.2
Elipsoide
Definição 8.2.1. O elipsoide é a superfície representada pela equação
x2 y 2 z 2
+ 2 + 2 =1
a2
b
c
em que todos os coeficientes dos termos do primeiro membro dessa equação são
positivos, sendo que a, b e c representam as medidas dos semieixos do elipsoide.
Embora a terra seja usualmente modelada por uma esfera, um modelo mais
preciso é o elipsoide, pois a rotação da terra causa um achatamento nos polos.
O traço no plano xOy é a elipse
x2 y 2
+ 2 =1
a2
b
e os traços nos planos xOz e yOz são as elípses
x2 z 2
+ 2 =1
a2
c
e
y2 z2
+ 2 =1
b2
c
150
respectivamente.
Se pelo menos dois dos valores a, b e c são iguais, o elipsoide é de revolução.
Por exemplo, se a = c, o elipsoide é obtido girando a elipse
y2 z2
+ 2 =1
b2
c
do plano yOz em torno do eixo das ordenadas.
O traço no plano xOz é a circunferência
x2 z 2
+
=1
4
4
No caso de a = b = c a equação
x2 y 2 z 2
+ 2 + 2 =1
a2
b
c
toma a forma
x2 + y 2 + z 2 = a2
e representa uma superfície esférica de centro C(0, 0, 0) e raio a.
Se o centro do elipsoide é o ponto C(x0 , y0 , z0 ) e seus eixos forem paralelos aos
eixos coordenados, sua equação assumirá a forma
(x − x0 )2 (y − y0 )2 (z − z0 )2
+
+
=1
a2
b2
c2
obtida através de uma translação de eixos.
De maneira análoga, a superfície esférica de centro C(x0 , y0 , z0 ) e raio a tem
equação
151
(x − x0 )2 + (y − y0 )2 + (z − z0 )2 = a2
8.3
Hiperboloide de uma Folha
Definição 8.3.1. A equação
x2 y 2 z 2
+ 2 − 2 =1
a2
b
c
representa um hiperboloide de uma folha ao longo do eixo z. As outras formas
x2 y 2 z 2
− 2 + 2 =1
a2
b
c
e
−
x2 y 2 z 2
+ 2 + 2 =1
a2
b
c
representam hiperbolóides de uma folha ao longo dos eixos das ordenadas e das
abscissas, respectivamente.
Você sabia que torres de resfriamento para reatores nucleares são usualmente
projetadas na forma de hiperboloides de uma folha, por razões de estabilidade
estrutural?
152
O traço no plano xOy da equação
x2 y 2 z 2
+ 2 − 2 =1
a2
b
c
é a elípse
x2 y 2
+ 2 =1
a2
b
e os traços nos planos xOz e yOz são as hipérboles
x2 z 2
− 2 =1
a2
c
e
y2 z2
− 2 =1
b2
c
respectivamente.
Um traço no plano z = k é uma elípse que aumenta de tamanho a medida que
o plano se afasta do plano xOy. Os traços nos planos x = k e y = k são
hipérboles.
Se na equação
x2 y 2 z 2
+ 2 − 2 =1
a2
b
c
tivermos a = b, o hiperboloide é de revolução, gerado pela rotação de uma
hipérbole em torno de seu eixo não focal, no caso, o eixo z.
153
8.4
Hiperboloide de Duas Folhas
Definição 8.4.1. A equação
−
x2 y 2 z 2
+ 2 − 2 =1
a2
b
c
representa um hiperboloide de duas folhas ao longo do eixo das ordenadas.
As equações
x2 y 2 z 2
− 2 − 2 =1
a2
b
c
e
−
x2 y 2 z 2
− 2 + 2 =1
a2
b
c
representam hiperboloides de duas folhas ao longo do eixo das abscissas e do
eixo Oz, respectivamente.
Os traços da superfície
−
y2 z2
x
+
− 2 =1
a2 b2
c
nos planos xOy e yOz são, respectivamente, as hipérboles
154
y 2 x2
− 2 =1
b2
a
y2 z2
− 2 =1
b2
c
O plano xOy não intercepta a superfície, nem qualquer plano y = k, onde
| k |< b.
Se | x |> b, o traço no plano y = k é a elípse
x2 z 2
k2
+
=
−1
a2
c2
b2
Os traços nos planos x = k e z = k são hipérboles.
Se na equação
−
x2 y 2 z 2
+ 2 − 2 =1
a2
b
c
tivermos a = c, o hiperboloide é denominado de revolução, gerado pela rotação
de uma hipérbole em torno de seu eixo focal. O traço no plano y = k,| x |> b,
é a circunferência
−
x2 k 2 z 2
+ 2 − 2 =1
a2
b
a
ou
x2 z 2
k2
+
=
−1
a2 a2
b2
155
8.5
Paraboloide Elíptico
Definição 8.5.1. A equação
x2 y 2
+ 2 = cz
a2
b
representa um paraboloide elíptico ao longo do eixo z. As equações
x2 z 2
+ 2 = bz
a2
c
e
y2 z2
+ 2 = az
b2
c
representam paraboloides elípticos ao longo dos eixos das ordenadas e abscissas,
respectivamente.
Os chamados paraboloides circulares, que são obtidos pela rotação de uma parábola em torno de seu eixo, são usados para coletar e refletir luz, som e sinais
de rádio e televisão. Em um radiotelescópio, por exemplo, sinais das estrelas
distantes que atingem a bacia são refletidos para o receptor no foco e assim
amplificados. O mesmo princípio se aplica a microfones e antenas de satélite
na forma de paraboloides.
156
Agora, se tomarmos a superfície de equação
x2 y 2
+ 2 = cz
a2
b
seu traço, no plano xOy, é a origem (0, 0, 0), e os traços, nos planos xOz e
yOz são as parábolas
x2
= cz,
a2
y2
= cz
b2
respectivamente.
Caso c > 0, a superfície situa-se inteiramente acima do plano xOy e, para
c < 0, a superfície situa-se inteiramente abaixo desse plano. Assim, o sinal de
c coincide com o de z, pois, caso contrário, não haveria tal superfície.
Um traço no plano z = k, k > 0 é uma elipse que aumenta de tamanho à
medida que o plano se afasta do plano xOy. Os traços nos planos x = k e
y = k são parábolas.
Se na equação
x2 y 2
+ 2 = cz
a2
b
tivermos a = b, o paraboloide é dito de revolução e pode ser gerado pela rotação
da parábola
y2
= cz
b2
em torno do eixo z. Nesse caso, o traço no plano z = k é uma circunferência.
157
8.6
Paraboloide Hiperbólico
Definição 8.6.1. A equação
y 2 x2
− 2 = cz
b2
a
representa um paraboloide hiperbólico ao longo do eixo z e as equações
z 2 x2
− 2 = by
c2
a
z2 y2
− 2 = ax
c2
b
representam paraboloides hiperbólicos situados ao longo dos eixos Oy e Ox,
respectivamente.
O traço da superfície
y 2 x2
− 2 = cz
b2
a
no plano xOy é o par de retas
y 2 x2
− 2 =0
b2
a
e os traços, nos planos xOz e yOz, são as parábolas
158
−
x2
= cz
a2
y2
= cz
b2
que têm o eixo z como eixo de simetria e concavidade para baixo e para cima,
respectivamente.
O traço no plano z = k é uma hipérbole cujo eixo focal é paralelo ao eixo
das ordenadas caso k seja positivo e paralelo ao eixo das abscissas caso k seja
negativo. Os traços nos planos x = k e y + k são parábolas.
8.7
Superfície Cônica
A expressão superfície cônica nos lembra algo familiar. A ideia de superfície
cônica é uma superfície gerada por uma reta que se move apoiada numa curva
plana qualquer e passando sempre por um ponto dado não situado no plano
desta curva. Vamos traduzir isso para uma linguagem mais adequada.
Definição 8.7.1. Seja γ uma curva contida num plano π do espaço e V um
ponto não pertencente a π. A superfície cônica S de diretriz γ e vértice V é a
superfície gerada por todas as retas que passam por V e por algum ponto de γ,
ou seja
−→
S = {V + tV P ; P ∈ γ, t ∈ R}
−→
As retas S = {V + tV P ; t ∈ R} com P ∈ γ são as geratrizes da superfície
cônica. Geometricamente a definição anterior pode ser ilustrada da forma a
seguir:
Consideremos o caso particular da superfície cônica cuja diretriz é uma elipse
159
( ou circunferência) com o vértice na origem do sistema e com seu eixo sendo
um dos eixos coordenados. Nestas condições, a superfície cônica cujo eixo é o
eixo z tem equação
x2 y 2 z 2
+ 2 − 2 =0
a2
b
c
O traço no plano xOy é o ponto (0, 0, 0). O traço no plano yOz tem equações
y2 z2
− 2 =0
b2
c
de onde obtemos duas retas que passam pela origem
b
y= z
a
e
b
y=− z
a
O traço no plano xOz, de forma análoga, é constituido por duas retas que
passam pela origem. Os traços nos planos z = k são elipses e se a = b são
circunfrências. Nesse caso, temos a superfície cônica circular reta. Os traços
nos planos x = k e y = k são hipérboles. As superfícies cônicas cujos eixos são
os eixos das abscissas e das ordenadas, tem equações
160
−
x2 y 2 z 2
+ 2 + 2 =0
a2
b
c
e
x2 y 2 z 2
− 2 + 2 =0
a2
b
c
respectivamente.
8.8
Superfície Cilíndrica
Informalmente, uma superfície cilíndrica é uma superfície gerada por uma reta
que se move paralelamente a uma outra reta fixa em contato permanente com
uma curva plana. De uma forma mais precisa, temos:
−
Definição 8.8.1. Seja γ uma curva contida num plano π do espaço e →
v um
vetor não nulo e não paralelo ao plano π. A superfície cilíndrica S de diretriz
→
γ e geratrizes paralelas ao vetor −
v é o conjunto
→
S = {P + t−
v ; P ∈ γ, t ∈ R}
Iremos considerar apenas superfícies cilíndricas cuja diretriz é uma curva que
se encontra em um dos planos coordenados e a geratriz é uma reta paralela
ao eixo coordenado não contido no plano. Neste caso a equação da superfície
cilíndrica é a mesma de sua diretriz.
Exemplo 8.8.1. Se a equação da diretriz for x2 = 2y, a equação da superfície
cilíndrica também será x2 = 2y.
Conforme a diretriz seja uma circunferência, elipse, hipérbole ou parábola, a
superfície cilíndrica é chamada de circular, elíptica, hiperbólica ou parabólica.
161
Agora, note que, em geral, o gráfico de uma equação que não contém uma
determinada variável corresponde a uma superfície cilíndrica cujas geratrizes
são paralelas ao eixo ausente e cuja diretriz é o gráfico da equação dada no
plano correspondente.
Exemplo 8.8.2. A equação
x2 z 2
+
=1
4
9
representa uma superfície cilíndrica com geratrizes paralelas ao eixo das ordenadas, sendo a diretriz uma elipse no plano xoz.
Atividades
1) Identifique as quádricas representadas pelas equações:
a) x2 + y 2 + z 2 = 25
b) 2x2 + 4y 2 + z 2 − 16 = 0
c) x2 − 4y 2 + 2z 2 = 8
d) z 2 = x2 + y 2
e) x2 + y 2 = 9
162
Para Final de Conversa...
Que bom que você chegou ao final desta disciplina. Essa chegada é fruto de sua vontade,
dedicação e persistência. Sabemos que não foi fácil essa caminhada.
Certamente, ao cursar esta disciplina, você revisou vários conteudos e adquiriu novos
conhecimentos, que serão indispensáveis para você continuar seus estudos em Matemática,
além de proporcionar a você mais autoconfiança em sua vida profissional.
Desejamos-lhe muito sucesso em seus estudos. Estamos felizes por termos feito parte
dessa etapa de sua vida.
Os Autores.
163
Referências
WINTERLE ,P.; STEINBRUCH, A. Geometria Analítica. São Paulo: Pearson Makron Books,
2006.
BOULOS ,P.; CAMARGO, I. Introdução a Geometria Analítica no Espaço. São Paulo:
Makron Books, 1997.
LIMA, E. L. Coordenadas no Espaço. Rio de Janeiro: Projeto Euclides, 1993.
VENTURI, J. Álgebra Vetorial e Geometria Analítica. Editora Unificado, Curitiba, 2000.
VENTURI, J. Cônicas e Quádricas. Editora Unificado, Curitiba, 1994.
165