Lançamento Oblíquo

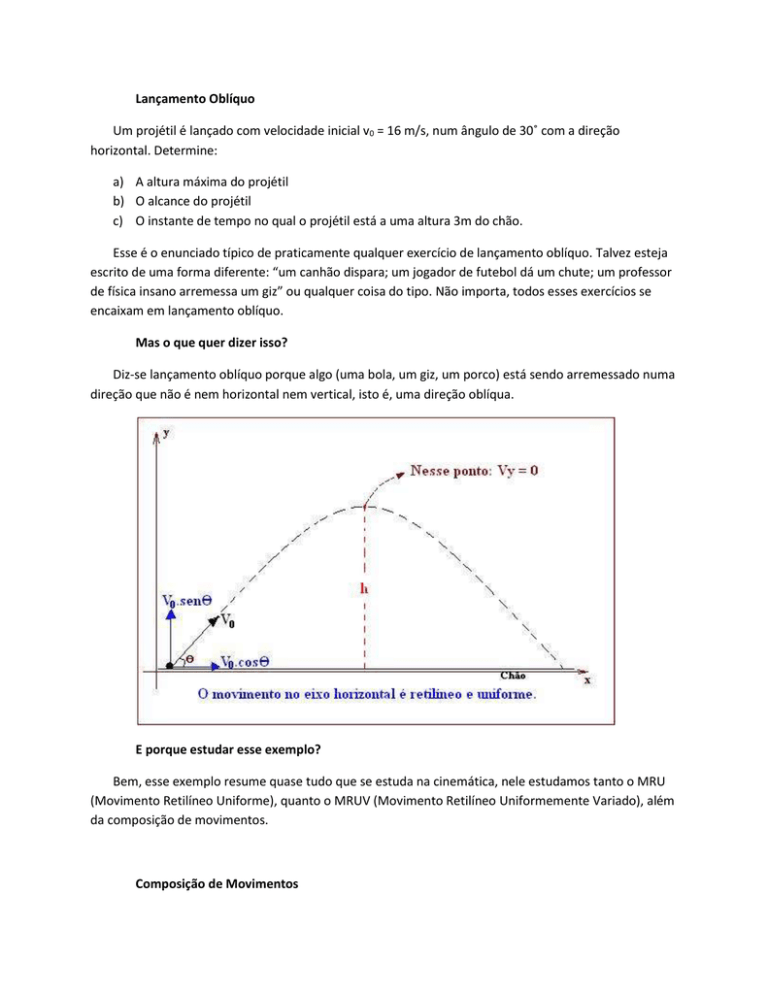
Lançamento Oblíquo
Um projétil é lançado com velocidade inicial v0 = 16 m/s, num ângulo de 30˚ com a direção
horizontal. Determine:
a) A altura máxima do projétil
b) O alcance do projétil
c) O instante de tempo no qual o projétil está a uma altura 3m do chão.
Esse é o enunciado típico de praticamente qualquer exercício de lançamento oblíquo. Talvez esteja
escrito de uma forma diferente: “um canhão dispara; um jogador de futebol dá um chute; um professor
de física insano arremessa um giz” ou qualquer coisa do tipo. Não importa, todos esses exercícios se
encaixam em lançamento oblíquo.
Mas o que quer dizer isso?
Diz-se lançamento oblíquo porque algo (uma bola, um giz, um porco) está sendo arremessado numa
direção que não é nem horizontal nem vertical, isto é, uma direção oblíqua.
E porque estudar esse exemplo?
Bem, esse exemplo resume quase tudo que se estuda na cinemática, nele estudamos tanto o MRU
(Movimento Retilíneo Uniforme), quanto o MRUV (Movimento Retilíneo Uniformemente Variado), além
da composição de movimentos.
Composição de Movimentos
Entender a composição de movimentos é o ponto chave para resolver problemas de lançamento de
projéteis. Pode parecer muito complicado estudar o movimento de um objeto lançado, mas podemos
simplificá-lo ao separar o movimento em duas direções: Vertical e Horizontal.
E porque podemos fazer isso?
Porque só há uma força atuando no objeto durante todo o movimento, a força gravitacional. Ela
atua somente na vertical, portanto o movimento na horizontal não é afetado.
Na vertical, como há uma força constante atuando, o movimento é retilíneo uniformemente variado.
Isso quer dizer que a velocidade do objeto irá variar com o tempo. Na horizontal, o movimento é
retilíneo uniforme, portanto a velocidade do objeto será constante.
Movimento vertical:
Para resolver o movimento horizontal utilizamos três equações fundamentais:
A equação horário do movimento, que tem o nome de “horária” pois é uma função do tempo, isso
quer dizer que determinamos o valor de y dependendo dos valores de t:
𝑦 = 𝑦𝑜 + 𝑣𝑜𝑦 𝑡 +
𝑎𝑡²
2
y = a posição do objeto em um determinado instante de tempo
yo = posição inicial do objeto
𝑣𝑜𝑦 = é a velocidade inicial do objeto
a = aceleração do objeto
t = instante de tempo.
A equação da velocidade:
𝑣𝑦 = 𝑣𝑜𝑦 + 𝑎𝑡
E ainda podemos deduzir uma terceira equação a partir dessas duas. Para isso basta isolar o tempo
na equação da velocidade e substituir na equação horária do movimento. A álgebra dessa operação fica
um pouco cansativa, por isso vamos direto ao resultado:
𝑣𝑦 ² = 𝑣𝑜𝑦 ² + 2𝑎(𝑦 − 𝑦𝑜 )
Ou ainda:
𝑣𝑦 ² = 𝑣𝑜𝑦 ² + 2𝑎∆𝑦
Onde ∆𝑦 é a variação da posição do objeto. Veremos como utilizar essas três equações durante a
resolução do exercício.
Movimento horizontal:
Esse caso é mais simples, pois a aceleração é nula e, como consequência, a velocidade é constante.
Temos apenas uma equação:
𝑥 = 𝑥𝑜 + 𝑣𝑜 𝑡
Resolução do exercício:
Agora que já temos as ferramentas necessárias, vamos voltar ao problema. O primeiro passo é
interpretar o que o problema está dizendo. Isso quer dizer que devemos extrair do enunciado as
informações que são dadas e entender que informação devemos obter.
“Um projétil é lançado com velocidade inicial v0 = 16 m/s, num ângulo de 30˚ com a direção
horizontal.”
Em destaque estão todas as informações necessárias para resolvermos o problema. Os enunciados
podem ser muito confusos às vezes, e por isso é bom prestar bastante atenção na leitura deles. Algumas
vezes tem somente uma ou duas informações fundamentais.
O próximo passo é decompor o movimento, dividi-lo no eixo x (horizontal) e no eixo y (vertical). Para
isso, precisamos decompor a velocidade. Utilizaremos para tal a trigonometria, vejamos como.
Primeiramente, vamos desenhar o nosso vetor velocidade, com o ângulo de 30 graus.
Agora ficou mais fácil visualizar o que devemos fazer. No que consiste essa tal de decomposição dos
vetores? Consiste em calcular a projeção do vetor nos eixos x e y. É mais ou menos como “medir a
sombra do vetor” nos eixos. Se somarmos Vx e Vy vetorialmente (isto é, colocar “o rabo” de um na ponta
do outro) teremos novamente o vetor V.
E como fazemos para determinar o valor de Vx e Vy? Basta usar as relações trigonométricas de seno
e cosseno. Se estivermos medindo a componente adjacente ao ângulo (isto é, colada no ângulo),
usamos o cosseno. No desenho acima, usaríamos o cosseno para determinar a componente Vx do vetor
V. Se medirmos a componente oposta ao ângulo, utilizamos o seno. No caso do vetor V acima,
utilizaríamos o seno para medir a componente Vy. Vamos tentar com a velocidade que foi nos dada
nesse problema:
V0 = 16 m/s, como o ângulo mede 30˚ com a horizontal, vamos precisar dos valores de sen 30˚ e cos
30˚. Esses valores são tabelados e nesse caso valem: sen 30˚ = 1/2 e cos 30˚ =
A componente Vx está adjacente ao ângulo (igual na figura), portanto vale:
𝑣𝑥 = 𝑣0 cos 30°
𝑣𝑥 = 16 ∙ cos 30°
√3
.
2
𝑣𝑥 = 16 ∙
√3
2
𝑣𝑥 = 16 ∙
√3
2
𝑣𝑥 = 8√3
Como √3 ≅ 1,73 (≅ significa aproximadamente)
𝑣𝑥 = 13,85 ≅ 14
Agora devemos calcular a componente y da velocidade, seguindo o mesmo procedimento:
𝑣𝑦 = 𝑣0 sen 30°
𝑣y = 16 ∙ sen 30°
𝑣𝑦 = 16 ∙
1
2
𝑣𝑦 = 16 ∙
1
2
𝑣𝑦 = 8
Agora já possuímos as velocidades nos dois eixos, vamos determinar as equações de movimento do
projétil:
No eixo X:
𝑥 = 𝑥0 + 𝑣0𝑥 𝑡
Como o exercício não diz a partir de qual posição o objeto foi lançado, podemos utilizar x0 = 0. Caso
o problema nos dissesse a posição inicial, deveríamos utilizá-la aqui. Lembrando sempre que o eixo X, no
nosso caso, está relacionado ao movimento vertical. A velocidade que devemos utilizar é 𝑣𝑥 :
𝑥 = 0 + 14𝑡
𝑥 = 14𝑡
Essa é a equação do movimento na direção horizontal. Para a vertical temos:
𝑦 = 𝑦𝑜 + 𝑣𝑜𝑦 𝑡 +
𝑎𝑡²
2
O problema não nos diz a partir de qual altura o objeto foi lançado, portanto podemos considerar
𝑦𝑜 = 0. Para 𝑣𝑜𝑦 utilizaremos a velocidade da componente y que calculamos e para 𝑎 utilizaremos 𝑔 =
−10 𝑚/𝑠², pois a única aceleração é a gravitacional. Aqui colocamos um sinal negativo pois o eixo de
coordenadas está definindo que no sentido para cima os vetores são positivos. Se olharmos a figura 2,
notamos que o vetor g está apontando para baixo, nesse caso, no sentido contrário ao que definimos
como positivo. Portanto, utilizamos um sinal de menos para indicar.
𝑦 = 0 + 8𝑡 +
(−10)𝑡²
2
𝑦 = 8𝑡 − 5t²
Essa é a equação do movimento vertical. Ainda podemos determinar a equação para a velocidade:
𝑣𝑦 = 𝑣𝑜𝑦 + 𝑎𝑡
Utilizando as mesmas informações para 𝑣𝑜𝑦 e 𝑎, teremos:
𝑣𝑦 = 8 − 10𝑡
Vamos enfim, responder às questões do problema:
a) Altura máxima do projétil:
Vamos analisar o movimento do projétil. A altura máxima está relacionada ao movimento na
vertical, portanto é essa parte que nos interessa. O movimento é bastante simples:
- O projétil sobe
- Para no ar
- E cai.
Num primeiro momento o projétil está subindo, portanto sua velocidade será positiva. Lembrando
que a velocidade é a variação da posição com o tempo, portanto, se ela é positiva, quer dizer que a
posição que estamos medindo está aumentando. No caso do nosso referencial, é o mesmo que dizer
que a altura do projétil está aumentando, portanto, ele está subindo. Como a aceleração é negativa, a
velocidade do projétil diminuirá até se tornar zero. Nesse momento, ele para no ar. Isso quer dizer que
sua velocidade é igual a zero, e a aceleração negativa. No momento seguinte, sua velocidade começa a
se tornar negativa. Isso quer dizer que a altura que estamos medindo está diminuindo, portanto o
objeto está caindo.
O que concluímos disso?
Concluímos que a altura máxima é atingida no ponto em que a velocidade do objeto se torna zero,
pois logo após isso o objeto começará a cair. Vamos então calcular a altura máxima do projétil, primeiro
devemos determinar o instante de tempo t em que a velocidade se torna zero.
0 = 8 − 10𝑡
Isolando t:
10t = 8
t=8s
O que acabamos de calcular é o tempo de subida do projétil. Após 1,4 segundos ele terá
atingido sua altura máxima. Para determinar o valor dessa altura basta substituir 1,4 na equação do
movimento vertical:
𝑦 = 8𝑡 − 5t²
𝑦 = 8 ∙ 0,8 − 5 ∙ (0,8)²
𝑦 = 6,4 − 5 ∙ (0,64)
𝑦 = 6,4 − 3,2 = 3,2 m
Portanto a altura máxima que o projétil atinge é 3,2m e está respondida a primeira parte da
questão.
b) O alcance do projétil.
O alcance se refere à distância horizontal que o projétil percorre. Se considerarmos que o chão é
plano, ele atingirá o chão novamente quando a altura for zero, isto é, y = 0. Vamos calcular então o
tempo que ele demora para voltar ao chão:
𝑦 = 8t − 5t²
0 = 8t − 5t²
Ou, reescrevendo:
5t² − 8t = 0
Temos uma equação de segundo grau. Podemos resolvê-la utilizando a forma de Bhaskara.
t=
−𝑏 ± √𝑏 2 − 4𝑎𝑐
2𝑎
Na nossa equação: a = 5; b = 8; e c = 0
t=
−(−8) ± √(−8)² − 4 ∙ (5) ∙ (0)
2 ∙ (5)
t=
8 ± √64)
10
t=
8±8
10
São, portanto, dois resultados possíveis:
t1 = 0
t2 =
16
= 1,6 𝑠
10
Mas o que quer dizer termos dois resultados para o tempo? Quer dizer que o projétil estará
nessa altura, nesse caso, altura zero, em dois instantes diferentes de tempo. Um deles é o instante de
tempo t= 0 que é imediatamente antes do objeto ser lançado. Portanto não é esse o instante de tempo
que nos interessa. Eliminando a alternativa t = 0, sabemos que o tempo de voo do objeto é de 1,6 s.
Certo, e como usar isso para determinar o alcance do objeto? Como foi dito, o alcance está relacionado
ao movimento horizontal, portanto devemos utilizar a equação do movimento horizontal:
𝑥 = 14𝑡
Substituindo t = 1,6
𝑥 = 14 ∙ 1,6
𝑥 = 22,4 𝑚
c) O instante de tempo no qual o projétil está a uma altura 3m do chão.
A diferença desse caso para os anteriores é que a informação que é nos dada agora é a altura,
portanto um valor de y. O que nos é pedido é um instante de tempo, portanto, t. Basta substituir o valor
de y na equação do movimento e determinarmos t.
𝑦 = 8𝑡 − 5t²
3 = 8𝑡 − 5t²
5t² − 8t + 3 = 0
Novamente temos uma equação de segundo grau. Resolvendo:
t=
t=
−𝑏 ± √𝑏 2 − 4𝑎𝑐
2𝑎
−(−8) ± √(−8)2 − 4 ∙ (5) ∙ (3)
2 ∙ (5)
t=
8 ± √64 − 60
10
t=
8 ± √4 8 ± 2
=
10
10
Novamente temos dois valores para t:
t1 =
t2 =
8 + 2 10
=
=1s
10
10
8−2
6
=
= 0,6 𝑠
10
10
Nesse caso, qual dos valores está correto? A resposta é os dois. Um deles, t = 0,6 s é referente à
subida do projétil. Enquanto sobe ele atinge y = 3m. Após isso ele continua subindo, atinge 3,2m de
altura e começa a cair. No movimento de queda, ele novamente passa pela altura y = 3m.