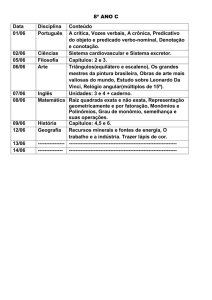
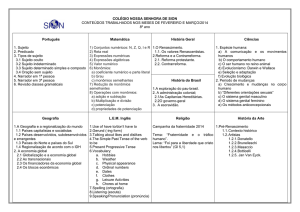
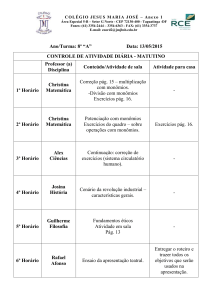
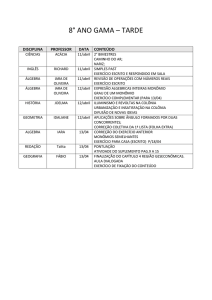
MATEMÁTICA
8° ANO
ENSINO FUNDAMENTAL
PROF. IVAIR TAVEIRA
PROF.ª REGINA COSTA
CONTEÚDOS E HABILIDADES
Unidade I
Linguagem Algébrica
2
CONTEÚDOS E HABILIDADES
Aula 3.1
Conteúdo
•• Monômios.
3
CONTEÚDOS E HABILIDADES
Habilidade
•• Reconhecer monômios, identificar o coeficiente e a
parte literal de um monômio e determinar o grau de um
monômio.
4
REVISÃO
Na aula anterior aprendemos sobre as expressões
algébricas e suas aplicações no nosso cotidiano. Vamos
relembrá-las?
5
REVISÃO
Tópicos da aula
Identificação das expressões algébricas.
Valor numérico de uma expressão algébrica identificada.
Aplicações das expressões algébricas.
6
DESAFIO DO DIA
Essas imagens podem ser representadas algebricamente?
Há alguma diferença e semelhança entre essas formas
algébricas?
7
AULA
Monômios
Toda expressão algébrica que possui apenas o produto de
constantes e variáveis recebe o nome de monômio, ou termo
algébrico.
A notação algébrica determina que deve-se usar as últimas
letras do alfabeto para representar as variáveis, e as
primeiras para representar as constantes, ou seja, x, y, z, t,
etc., são usados como variáveis, e a, b, etc., são usados para
representar constantes.
8
AULA
Exemplos de monômios
10xy
-45wt
-0,25x
½ mn
2a
9
AULA
As partes de um monômio
São divididos em duas partes: um número, denominado
coeficiente do monômio, e uma variável – ou produto de
variáveis (letras), mesmo que existam potências.
4y – neste monômio, temos o coeficiente (4), e a parte
literal (y).
10
AULA
5xy³ – neste caso, o coeficiente é o 5, e a parte literal é xy³,
lembrando sempre de incluir a potência.
x – quando não houver números explícitos, como o caso
ao lado, o coeficiente será 1. A parte literal continua sendo
identificada pelas últimas letras do alfabeto, no caso x.
11
AULA
Qual o coeficiente e a parte literal dos monômios?
Monômios
Coeficiente
Parte literal
7sz
-95r³m²n
12
DINÂMICA LOCAL INTERATIVA
Qual o coeficiente e a parte literal dos monômios?
Monômios
Coeficiente
Parte literal
6r³s²
-78xy²z
0,5wt
13
AULA
Grau de um monômio
O grau dos monômios cujos coeficientes não são nulos é
indicado pela soma dos expoentes da parte literal.
14
AULA
Exemplos:
4x²y³
Expoente da variável x é 2.
Expoente da variável y é 3.
2+3=5
Portanto, 4x²y³ é um monômio do 5° grau.
15
AULA
23m¹n²
Expoente da variável a é 1.
Expoente da variável b é 2.
1+2=3
Portanto, 23mn² é um monômio do 3° grau.
16
AULA
Qual o grau dos monômios?
Monômios
Grau
7sz
-95r³m²n
17
DINÂMICA LOCAL INTERATIVA
Qual o grau dos monômios?
Monômios
Grau
-6r³s²
78xy²z
10wt
18