potência operação possuem

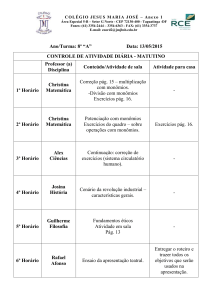
Considere as situações:
 1ª situação:
 Observe as dimensões da figura a seguir. Qual a
expressão que representa a sua área?
X
X
x2 ou x . x
 2ª situação:
 Deseja-se cercar um terreno de forma retangular cujo
comprimento e largura medem, respectivamente, 3x e y.
Quantos metros de tela deve-se comprar?
3x
y
 Devemos calcular o perímetro do terreno:
3x + 3x + y + y ou 6x + 2y
 3ª situação:
Mari tinha x reais. Foi a uma a lanchonete e tomou
2 sorvetes. Cada sorvete custou y reais. Qual a
expressão algébrica que representa a quantia que
restou para Mari depois que pagar os sorvetes?
 Como cada sorvete custou y reais, ela
gastou 2y reais.
 Então, a expressão algébrica pedida é: x – 2y.
 Nas situações apresentadas, escrevemos expressões
matemáticas nas quais aparecem números e letras, ou
somente letras. Essas expressões matemáticas são
chamadas algébricas ou literais.
AGORA É COM VOCÊS!!
Uma escola tem x alunos. Qual a expressão algébrica
que representa:
 O triplo do número de alunos.
 O número de alunos que a escola teria se entrassem 52
alunos.
 O número de alunos que a escola teria se saíssem 20
alunos.
Vejamos...
 Respostas:
 3x
 x + 52
 x - 20
VALOR NUMÉRICO DE UMA EXPRESSÃO ALGÉBRICA
 Na 3ª situação, onde Mari comprou 2 sorvetes, cada um
custando y reais e pagou com x reais. Vimos que o que
lhe restou de troco foi representado pela expressão
algébrica : x – 2y
 Agora, suponha que ela tivesse 50 reais e cada sorvete
custasse 2 reais.
 Neste caso, facilmente encontraríamos o que ela
recebeu de troco.
 Expressão algébrica que representa o troco:
 x – 2y
se x = 50 reais e y = 2 reais
 Temos então:
 50 – 2 . 2 ou 50 – 4
 Portanto, Mari recebeu de troco 46 reais.
EXERCÍCIO:
1) Qual é o valor numérico da expressão 4x – xy quando:
a) x = 2 e y = 6
b) x = 12 e y = - 2
 Observe:
 Vamos substituir as variáveis pelos números.
a) 4 . 2 – 2 . 6 = 8 – 12 = - 4
b) 4 . 12 – 12 . (- 2) = 48 + 24 = 72
Classificação das expressões algébricas
 IRRACIONAIS
 RACIONAIS
 Expressões algébricas irracionais são aquelas que
apresentam variáveis sob radicais.
 Exemplos:
 Expressões algébricas racionais são aquelas que não
apresentam variáveis sujeitas à operação radiciação.
 INTEIRAS
 FRACIONÁRIAS
 Exemplos:
2x + 3
4y
MONÔMIOS OU TERMOS ALGÉBRICOS
Considere a situação:
 Calcular a área de um terreno retangular, cujas dimensões
estão indicadas na figura.
2y
x
A área: 2y . x ou simplesmente 2yx
 O termo acima que representa a área do terreno é
denominado de MONÔMIO.
Definição:
 Monômio é toda expressão algébrica racional inteira
que indica uma multiplicação entre números e
variáveis ou apenas entre variáveis.
 Exemplos:
5x2y
-2a3b2
 Em geral, um monômio é formado por uma parte
numérica, que chamamos de coeficiente, e de uma
parte literal.
 Por exemplo:
 10xy, temos que 10 é o coeficiente e xy é a parte literal.
 -23abc, temos que – 23 é o coeficiente e abc é a parte
literal.
Monômios semelhantes
 Definição: São aqueles que possuem a mesma parte
literal.
 Exemplos:
 2xy
– 8xy
49xy
12yx
OBSERVAÇÕES IMPORTANTES:
 Toda expressão algébrica composta de dois termos não
semelhantes é chamada de BINÔMIO. Veja estes exemplos:
Y + 4x
2m – 7x
 Toda expressão algébrica composta de três termos não
semelhantes é chamada de TRINÔMIO. Veja estes
exemplos:
a + 4x – y
x + y – 5z
 De modo geral, toda expressão algébrica constituída de
monômios é chamada de POLINÔMIO.
OPERAÇÕES COM MONÔMIOS
 Adição e Subtração:
 Considere uma figura de forma retangular, cuja a
medida do comprimento é o triplo da medida da
largura.
 a) Escreva a expressão algébrica que representa o
perímetro desse retângulo.
Temos que: largura = x comprimento = 3x
O perímetro desse retângulo será:
3x + 3x + x + x = 8x
Nesta questão, resolvemos uma adição de monômios
 b) Escreva agora, a expressão algébrica que representa
a diferença entre a medida do comprimento e a medida
da altura.
 Temos que: comprimento = 3x
 Portanto, a diferença será:
altura = x
3x – x = 2x
 Neste caso, teremos uma subtração de monômios.
 ATENÇÃO!
 A adição e subtração de monômios só pode ser feita
quando os termos envolvidos são semelhantes. Nesse
caso, adicionamos ou subtraímos os coeficientes e
conservamos a parte literal.
EXERCÍCIO
 1) Efetue as seguintes adições e subtrações de
monômios.
 3x + 6x =
 4y -2y =
 1,2xy + 3xy – 0,2xy =
Polinômio reduzido
 Um polinômio que possui termos semelhantes pode ser
escrito numa forma mais simples chamada FORMA
REDUZIDA. Para isso, basta efetuarmos a adição e
subtração dos coeficientes dos monômios semelhantes,
conservando a parte literal desses monômios.
 Exemplo: 3x + 6x + 5y – 3y = 9x + 2y
MULTIPLICAÇÃO E DIVISÃO DE MONÔMIOS
 Considere que as dimensões de um retângulo sejam 3x
e 2x, conforme a figura abaixo:
3x
2x
 Para calcularmos a área devemos multiplicar essas
dimensões, então teremos:
3x . 2x = (3 . 2) .(x . x) = 6 x2
Devemos observar que quando multiplicamos
monômios, multiplicamos os coeficientes e a parte
literal.
 Exemplos:
2x .2x = (2.2) . (x.x) = 4x²
(3a2b) . (5ab3) = (3.5) . (a2.a) . (b .b3) = 15 . (a 2 +1) . (b 1 + 3) = 15 a3 b4
OBSERVAÇÃO:
 Se a parte literal for a mesma, usamos a propriedade de
potência.
Lembrar...
Potências de mesma base; conserva-se a base e soma-se
os expoentes.
am . an = am + n
 Se a parte literal for diferente, basta deixá-la indicada
no produto.
 Outros exemplos:
 2x . 3y = 6xy
 20c . 2ab = 40abc
 x . 6a = 6xa
 A figura abaixo representa parte do piso de um quarto, cuja
forma é retangular. Esse piso será coberto por lajotas de forma
quadrada, conforme abaixo:
2y
12y2
2y
20y2
a) Determine o monômio que representa a área total do piso do
quarto.
b) Determine o monômio que representa a área de cada lajota.
c) Determine o monômio que representa a quantidade de lajotas
necessária para cobrir totalmente o piso desse quarto.
d) Considerando y = 1, calcule a quantidade de lajotas necessárias
para cobrir o piso dessa sala.
 Resolvendo o que foi pedido, temos:
 a)20y2 . 12y2 = (20.12) . (y2.y2) = 240y4
 b) 2y . 2y = (2.2) . (y.y) = 4y2
 c) 240y4 :4y2 = (240:4) . (y4:y2) = 60y2
 d) 60y2 = 60 . 1 = 60 lajotas
 Nesse caso, efetuamos uma divisão entre monômios.
 Devemos observar que quando dividimos monômios,
dividimos os coeficientes e a parte literal.
OBSERVAÇÃO:
Se a parte literal for a mesma, usamos a propriedade de
potência.
Lembrar...
Divisão de potências de mesma base, conserva-se a
base e subtraí-se os expoentes.
am : an = am - n
Se a parte literal for diferente, basta deixá-la indicada
no quociente.
 Exemplos:
 6x3 : 3x = 6 . x3 = 2x2
3 x
 -10x2y4 : 2xy2 = -10 x2 y4 = -5xy2
2 x y2