QUADRILÁTEROS.

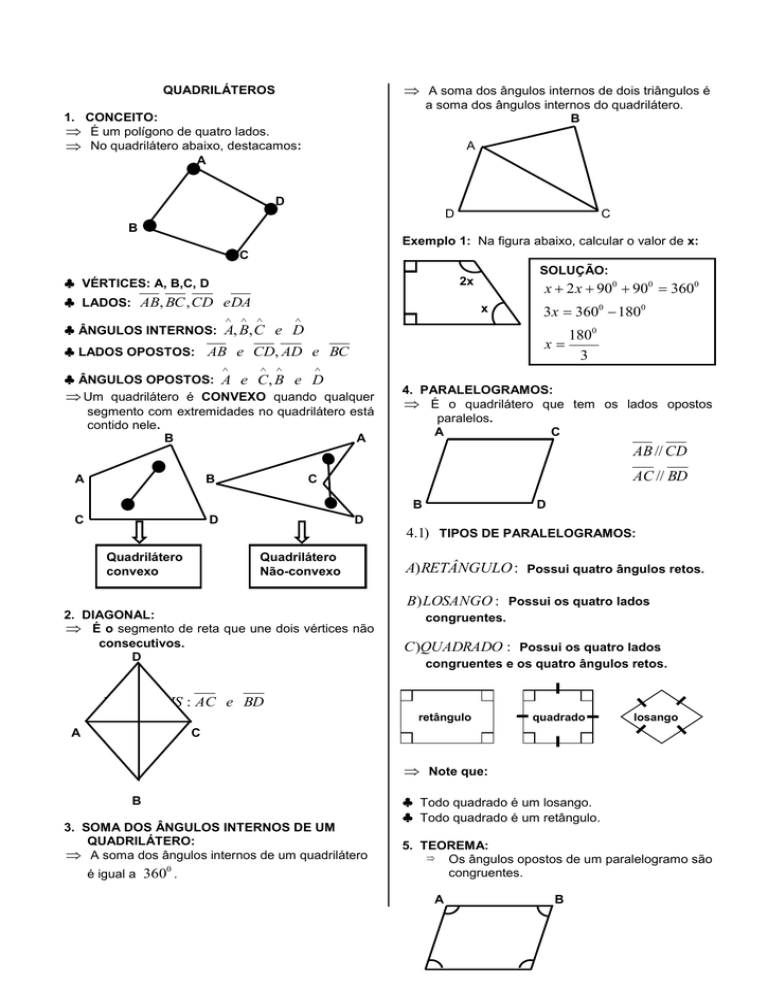
 A soma dos ângulos internos de dois triângulos é
QUADRILÁTEROS
a soma dos ângulos internos do quadrilátero.
B
1. CONCEITO:
 É um polígono de quatro lados.
 No quadrilátero abaixo, destacamos:
A
A
D
D
C
B
Exemplo 1: Na figura abaixo, calcular o valor de x:
C
SOLUÇÃO:
2x
♣ VÉRTICES: A, B,C, D
♣ LADOS: AB, BC , CD e DA



x  2 x  900  900  3600
x

♣ ÂNGULOS INTERNOS: A, B, C e D
1800
3
x  600
x
♣ LADOS OPOSTOS: AB e CD, AD e BC



3x  3600  1800

♣ ÂNGULOS OPOSTOS: A e C , B e D
 Um quadrilátero é CONVEXO quando qualquer
segmento com extremidades no quadrilátero está
contido nele.
B
A
4. PARALELOGRAMOS:
 É o quadrilátero que tem os lados opostos
paralelos.
A
C
AB // CD
A
B
C
D
AC // BD
C
B
D
D
4.1) TIPOS DE PARALELOGRAMOS:
Quadrilátero
convexo
Quadrilátero
Não-convexo
A)RETÂNGULO : Possui quatro ângulos retos.
B)LOSANGO : Possui os quatro lados
2. DIAGONAL:
 É o segmento de reta que une dois vértices não
consecutivos.
D
congruentes.
C )QUADRADO : Possui os quatro lados
congruentes e os quatro ângulos retos.
DIAGONAIS : AC e BD
retângulo
A
quadrado
losango
C
 Note que:
B
3. SOMA DOS ÂNGULOS INTERNOS DE UM
QUADRILÁTERO:
 A soma dos ângulos internos de um quadrilátero
0
é igual a 360 .
♣ Todo quadrado é um losango.
♣ Todo quadrado é um retângulo.
5. TEOREMA:
 Os ângulos opostos de um paralelogramo são
congruentes.
A
B




AD
BC
C
a)
b)
c)
d)
Todo quadrado é um losango.
Todo quadrado é um retângulo.
Todo paralelogramo é um quadrilátero.
Um losango pode não ser um paralelogramo.
D
Exemplo 1: Na figura abaixo, calcular o valor de x:
3 x  100
SOLUÇÃO:
3 x  100  x  500
x  50
3 x  x  500  100
0
2 x  60
0
3. (FRANCO) As medidas dos ângulos internos de
um
quadrilátero
são
x,2 x,3x e 4 x ,
respectivamente. Então os ângulos desse
quadrilátero são:
a) Todos iguais a 36
0
600
x
 x  300
2
6. TRAPÉZIO:
 É o quadrilátero que possui dois lados
paralelos (que são chamados de base).
0
0
0
b)
0
18 ,36 ,54 ,72
0
0
0
0
c) 36 ,72 ,108 ,144
90 ,180 ,270 ,360
d)
4. (FRANCO) Um quadrilátero convexo PQRS tem



ângulos internos P  90 , Q  120 , R  60 . O
0
0
0

ângulo interno S do quadrilátero vale:
a) 60
0
100
b) 70
0
c) 90
0
d)
0
Base menor
A
B
AB// CD
altura
C
5. (FRANCO) Na figura ao lado, o valor de x:
0
D
550
a) 55
Base maior
0
b) 65
OBS: A distância entre as bases chama-se altura.
1300
0
c) 75
0
d) 85
700
x
6.1) TIPOS DE TRAPÉZIO :
6. (FRANCO) Na figura ao lado, o valor de x:
A)ISÓSCELES : Os lados não-paralelos são
congruentes.
a) 20
b) 30
B)RETÂNGULO : Tem dois ângulos retos.
0
4x
0
0
c) 35
d) 40
2x
0
C )ESCALENO : Os lados não-paralelos não são
7. (FRANCO) Dois segmentos que têm a mesma
medida são chamados:
congruentes.
Trapézio
Isósceles
Trapézio
Retângulo
Trapézio
Escaleno
TESTES
400 e 1400
0
0
b) 140 e 40
0
0
c) 130 e 50
0
0
d) 50 e 130
a)
40 0
y
x
1. (FRANCO) Um polígono de 4 lados chama-se:
a) quadrado
b) paralelogramo
b) retângulo
d) n. d. a
2. (FRANCO) A afirmação falsa é:
8. (FRANCO) Os valores de x e y no paralelogramo
abaixo são, respectivamente:
1250 e 550
0
0
b) 135 e 45
a)
x
1450 e 350
0
0
d) 135 e 55
c)
450
y
9. (FRANCO) No paralelogramo ao lado, o valor de x
é:
a) 32
3 x  100
0
0
b) 38
2 x  540
440
0
d) 64
c)
10. (FRANCO) No paralelogramo ao lado, o valor de
x é:
0
a) 40
0
b) 45
c) 50
d) 60
0
2 x  150
0
x  150
11. (FRANCO) No losango ao lado, o valor de x é:
a) 70
0
1500
0
b) 75
c) 60
0
x
0
d) 65
12.
(FRANCO)
  
Nesta
figura,
os
ângulos

a, b, c e d
medem, respectivamente,
x
3x
, 2 x,
e x. O
2
2


ângulo e é reto. Qual a medida do ângulo f ?
a) 16
0
b) 18
c) 20
d)
c
0
b
0
22
f
d
a
0
G A B A R I T O
1. D
5. C
9. C
2. D
6. B
10. D
3. C
7. D
11. B
4. C
8. B
12. B
e