Material - SOL - Professor | PUC Goiás

Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
I.3 Indução de Árvores de Decisão
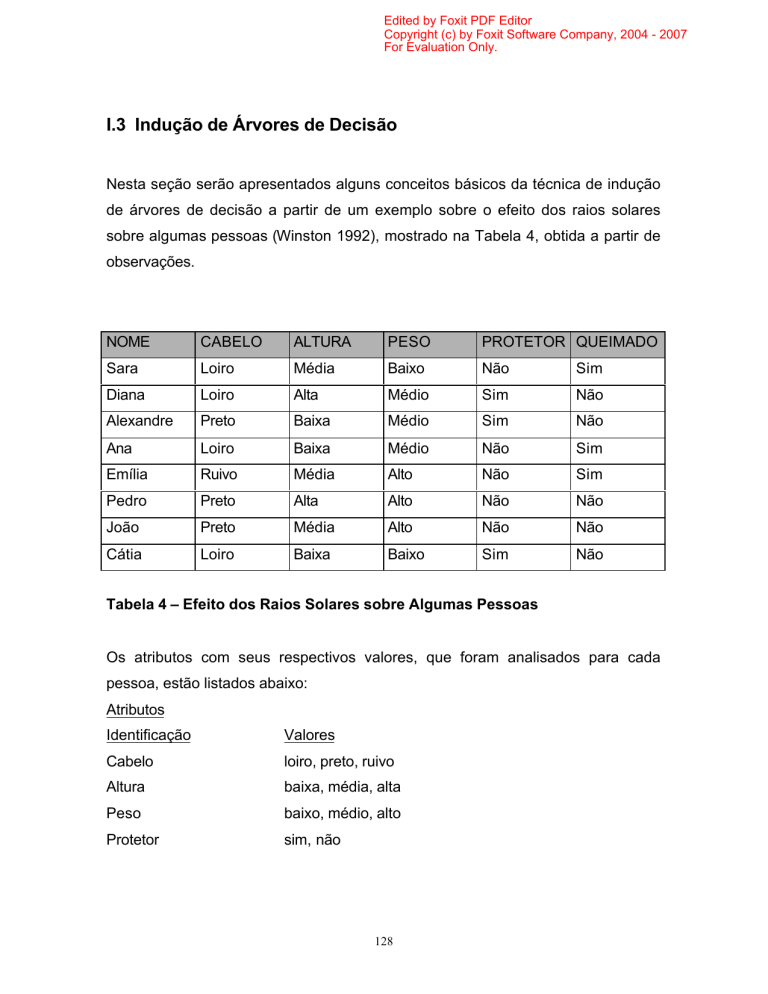
Nesta seção serão apresentados alguns conceitos básicos da técnica de indução
de árvores de decisão a partir de um exemplo sobre o efeito dos raios solares
sobre algumas pessoas (Winston 1992), mostrado na Tabela 4, obtida a partir de
observações.
NOME
CABELO
ALTURA
PESO
PROTETOR QUEIMADO
Sara
Loiro
Média
Baixo
Não
Sim
Diana
Loiro
Alta
Médio
Sim
Não
Alexandre
Preto
Baixa
Médio
Sim
Não
Ana
Loiro
Baixa
Médio
Não
Sim
Emília
Ruivo
Média
Alto
Não
Sim
Pedro
Preto
Alta
Alto
Não
Não
João
Preto
Média
Alto
Não
Não
Cátia
Loiro
Baixa
Baixo
Sim
Não
Tabela 4 – Efeito dos Raios Solares sobre Algumas Pessoas
Os atributos com seus respectivos valores, que foram analisados para cada
pessoa, estão listados abaixo:
Atributos
Identificação
Valores
Cabelo
loiro, preto, ruivo
Altura
baixa, média, alta
Peso
baixo, médio, alto
Protetor
sim, não
128
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
A classificação foi feita para o atributo categórico queimado, com os valores: sim
ou não.
O número de combinações dos valores dos atributos é 54. Este valor é obtido pela
multiplicação dos números de possíveis valores para cada atributo:
Cabelo = 3 (loiro, preto, ruivo);
Altura = 3 (baixa, média, alta);
Peso = 3 (baixo, médio, alto); e
Protetor = 2 (sim, não).
Ou seja, o resultado é obtido pela multiplicação destes valores: 3 * 3 * 3 * 2 = 54.
A probabilidade de uma nova ocorrência ter as mesmas propriedades de um caso
já observado é calculada pela divisão do número de casos já observados dividido
pelo número total de casos possíveis, ou seja, 8 / 54 = 0,15. Isto indica que a
probabilidade de uma nova informação casar exatamente com um dos casos já
observados é 15%.
Na prática, a probabilidade pode ser bem menor, pois pode haver muito mais
atributos e muito mais valores a eles associados. Por exemplo, supondo existir 12
atrubutos, cada um com 5 possíveis valores e cada valor aparecendo com igual
freqüência, haveria 512 combinações. Se a tabela tivesse um milhão de casos, a
probabilidade de um novo caso ser igual a um já existente seria cerca de 0,4 %
(= 1 milhão / 512 ).
Portanto, pode ser impraticável classificar um caso desconhecido buscando um
casamento exato com propriedades de casos conhecidos e classificados.
Os dados poderiam ser tratados com um espaço de características no qual
poderia-se buscar um casamento parcial. Porém, em não se sabendo quais
propriedades são importantes, pode-se encontrar um vizinho próximo devido a um
alinhamento coincidente de propriedades irrelevantes.
129
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Uma outra alternativa seria utilizar um procedimento de teste de propriedades que
classificasse corretamente cada um dos casos conhecidos, podendo ser usado
para classificar corretamente novos casos.
Os testes envolvidos podem ser arrranjados numa árvore de identificação, isto é,
numa árvore de decisão na qual cada conjunto de possíveis conclusões é
estabelecido implicitamente por uma lista de amostras de classes conhecidas,
como pode ser observado nas Figuras 11 e 12.
Cabelo
loiro
preto
ruivo
Alexandre
Pedro
João
Protetor
não
Sara
Ana
não
Diana
Cátia
Figura 11 – Árvore de Decisão Consistente com o Conjunto de Casos e com
a Intuição sobre os Efeitos dos Raios Solares na Pele das Pessoas
OBS – Em todas as Figuras desta seção, para facilitar o entendimento ao leitor, as
pessoas classificadas com atributo categórico com valor “sim”, estão destacadas
em negrito, para diferenciar das outras classificadas com valor “não”.
130
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Altura
alta
baixa
média
Diana
Pedro
Peso
Cabelo
baixo
ruivo
médio
loiro
preto
alto
Sara
Peso
Cabelo
loiro
Alexandre
baixo
médio
Cátia
ruivo
preto
alto
Emília
Ana
João
Figura 12 – Árvore de Decisão Consistente com o Conjunto de Casos, porém
Inconsistente com a Intuição sobre os Efeitos dos Raios Solares na Pele das
Pessoas
Intuitivamente, a árvore da Figura 11 parece ser melhor que a da Figura 12.
Porém, para um programa chegar a esta conclusão seria necessário um
especialista registrar estas informações ou então basear-se nos fundamentos da
lâmina de Occam e na teoria da Informação que serão descritos em seguida.
131
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Lâmina de Occam
O fundamento da lâmina de Occam (Occam’s razor) é baseado na teoria do
filósofo Ockham, que viveu no século XIII, de que o mundo é inerentemente
simples. Aplicando este fundamento às árvores de decisão pode-se concluir que a
menor árvore de identificação que for consistente com as amostras (casos) será
aquela que mais provavelmente irá classificar corretamente casos desconhecidos.
E a questão deixa, portanto, de ser “qual é a árvore de identificação correta?” e
passa a ser “como construir a menor árvore de identificação?”.
Para construir a menor árvore de identificação procura-se partir da característica
mais relevante, mais discriminante e a partir dela, descer a árvore. O objetivo é
selecionar o teste para o nó raiz que melhor divida os casos em subconjuntos
homogêneos (com a mesma classificação) e assim sucessivamente até que todos
os subconjuntos sejam homogêneos. Comparando-se os resultados obtidos nas
Figuras 13, 14, 15 e 16, observa-se que o teste da cor do cabelo (Figura 13) faz
uma melhor divisão dos casos em subconjuntos homogêneos. A Figura 17 mostra
que após isolar pessoas loiras, o teste de uso de protetor solar é o que faz a
melhor divisão desse conjunto em subconjuntos homogêneos.
132
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Teoria da Informação
A teoria da informação fornece uma fórmula para avaliar a desordem (entropia) de
uma árvore de decisão:
Desordem Média =
∑
Desordem Média =
∑ (nb / ni) * (∑ − nbc / nb log 2 nbc / nb)
b
((peso (do ramo)) * ( ∑ desordem de um ramo))
c
Onde:
nb = número de exemplos no ramo b;
ni = número de exemplos em todos os ramos; e
nbc = número de exemplos no ramo b da classe c.
Se um dado conjunto tivesse membros de apenas duas classes, por exemplo, A e
B, e o número de membros de cada classe fosse perfeitamente balanceado, a
desordem seria máxima e igual a 1:
Desordem =
∑ − nbc / nb log 2nbc / nb
c
Desordem = − 1 / 2 log 21 / 2 − 1 / 2 log 21 / 2 = ½ + ½ = 1
Por outro lado, se houvesse apenas membros da classe A ou apenas membros da
classe B, a desordem seria zero, pois no limite, quando x tende a zero, x log 2 x é
zero:
Desordem = − 1 / 1 log 21 − 0 / 1 log 20 = 0 – 0 = 0
Aplicando a fórmula da Desordem Média ao teste da cor do cabelo, obtém-se:
133
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Desordem Média = 4 / 8( −2 / 4 Log 22 / 4 − 2 / 4 log 22 / 4)
(para loiro)
+ 1/8 * 0
(para ruivo)
+ 3/8 * 0
(para preto)
= 0,5
Fazendo o mesmo para os outros testes obtém-se:
Teste
Desordem
Cabelo
0.5
Altura
0,69
Peso
0,94
Protetor
0,61
Após a seleção do teste do cabelo, para separar as pessoas do conjunto Sara,
Diana, Ana e Cátia, tem-se:
Teste
Desordem
Altura
0,5
Peso
1
Protetor
0
134
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Cabelo
preto
loiro
Sara
ruivo
Emília
Alexandre
Diana
Pedro
Ana
João
Cátia
Figura 13 – Teste da Cor do Cabelo
Peso
baixo
Sara
médio
alto
Diana
Emília
Alexandre
Pedro
Ana
João
Figura 14 – Teste do Peso
135
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Altura
baixa
alta
média
Alexandre
Sara
Diana
Ana
Emília
Pedro
Cátia
Figura 15 – Teste da Altura
Protetor
não
sim
Sara
Diana
Ana
Alexandre
Emília
Cátia
João
Pedro
Figura 16 – Teste de Uso de Protetor Solar
136
Edited by Foxit PDF Editor
Copyright (c) by Foxit Software Company, 2004 - 2007
For Evaluation Only.
Altura
baixa
média
Ana
alta
Diana
Sara
Cátia
Peso
alto
baixo
médio
Sara
Diana
Cátia
Ana
Protetor
não
sim
Sara
Diana
Ana
Cátia
Figura 17 – Teste de Uso de Protetor Solar após Isolar Pessoas Loiras
137