Colégio Jardim Paulista

Colégio Jardim Paulista
Nome:__________________________________________Nº______Série: 7º ano A
Prof:
Roberto
Início:________Término:________Data: _____/_____/______
Avaliação Bimestral de Matemática
Nota__________
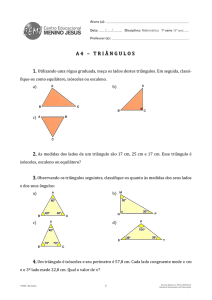
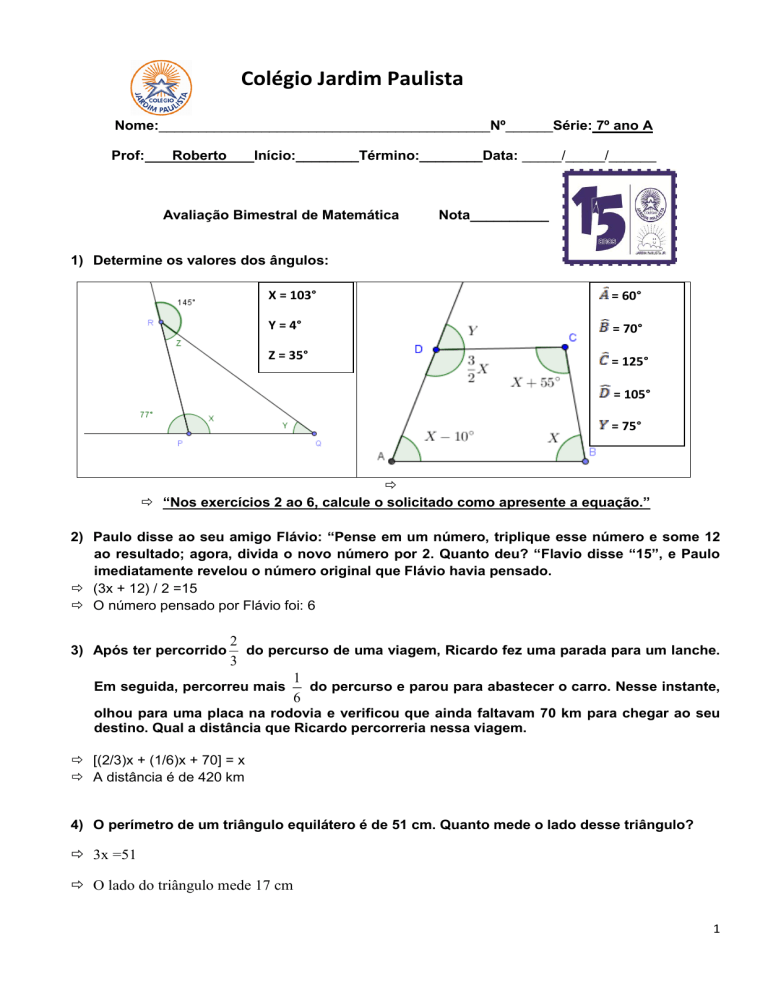
1) Determine os valores dos ângulos:
X = 103°
= 60°
Y = 4°
= 70°
Z = 35°
= 125°
= 105°
= 75°

 “Nos exercícios 2 ao 6, calcule o solicitado como apresente a equação.”
2) Paulo disse ao seu amigo Flávio: “Pense em um número, triplique esse número e some 12
ao resultado; agora, divida o novo número por 2. Quanto deu? “Flavio disse “15”, e Paulo
imediatamente revelou o número original que Flávio havia pensado.
 (3x + 12) / 2 =15
 O número pensado por Flávio foi: 6
2
do percurso de uma viagem, Ricardo fez uma parada para um lanche.
3
1
Em seguida, percorreu mais
do percurso e parou para abastecer o carro. Nesse instante,
6
3) Após ter percorrido
olhou para uma placa na rodovia e verificou que ainda faltavam 70 km para chegar ao seu
destino. Qual a distância que Ricardo percorreria nessa viagem.
 [(2/3)x + (1/6)x + 70] = x
 A distância é de 420 km
4) O perímetro de um triângulo equilátero é de 51 cm. Quanto mede o lado desse triângulo?
 3x =51
 O lado do triângulo mede 17 cm
1
5)



A soma de dois números naturais ímpares e consecutivos é 108. Quais são esses números?
X+ 1 + x + 3 = 108
2x + 4 = 108
Os números são 53 e 55
6) O perímetro de um triângulo escaleno é 363 cm. As medidas de seus lados são três números
naturais consecutivos. Determine-as.
 X + X + 1 + X + 2 = 363
 3x + 3 = 363
 As medidas dos lados do triângulo escaleno são: 120 cm; 121 cm; 123 cm
7) Resolva a equação:
X = -(59/16)
8) Resolva as inequações e represente a solução graficamente.
2x + 14 > 36, sendo
X > 11
9)



No plano cartesiano a seguir, a distância entre os pontos é de 1 cm.
Localize nesse plano cartesiano os pontos: A (1,1); B (6,1); C (8,3); D (3,3).
Ligue os pontos, formando uma figura geométrica, Que figura é essa? Paralelogramo
Calcule a área dessa figura.
2
10) Encontre a solução do sistema e apresente a representação gráfica da solução.
X
Y
(x , Y)
Solução
1,6
1,2
(1,6 , 1,2)
0
-2
(0 , -2)
1
0
(1 , 0)
0
2
(0 , 2)
4
0
(4 , 0)
Ponto
A
B
C
D
E
3