Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 4.ED., LTC, RIO DE
JANEIRO, 1996.
FÍSICA 2
CAPÍTULO 8 – CONSERVAÇÃO DA ENERGIA
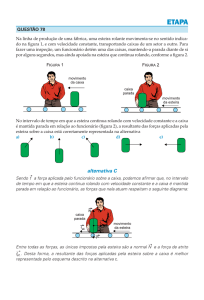
91. Numa fábrica, uma máquina de empacotamento deixa cair verticalmente um engradado de 300
kg numa esteira rolante que se move com uma velocidade de 1,20 m/s. (Fig. 8-56). (A
velocidade da esteira é mantida constante por um motor.) O coeficiente de atrito cinético entre o
engradado e a esteira é 0,400. Depois de um pequeno intervalo de tempo, o engradado deixa de
escorregar e passa a se mover com a mesma velocidade que a esteira. Para o intervalo de tempo
durante o qual o engradado está se movendo em relação à esteira, calcule, para um sistema de
coordenadas estacionário em relação à fábrica, (a) a energia cinética fornecida ao engradado, (b)
o módulo da força de atrito cinético que age sobre o engradado e (c) a energia fornecida pelo
motor. Por que as respostas de (a) e (c) são diferentes?
(Pág. 184)
Solução.
Considere a seguinte sequência de eventos que caracteriza a evolução do problema (vamos chamar
o “engradado” de “pacote” para evitar conflito de índices com a esteira):
1. Queda do pacote sobre a esteira, que se move com velocidade constante vE:
2. O pacote toca a esteira e começa a deslizar (derrapar) sobre ela. Nesse momento, a velocidade do
pacote (vP0) é nula.
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
3. O pacote continua deslizando sobre a esteira, mas sua velocidade está aumentando a cada
instante:
4. Após algum tempo, o pacote para de deslizar e adquire a mesma velocidade da esteira (vP2 = vE):
a) A energia cinética fornecida ao pacote (KP) é simplesmente:
1
1
1
2
K P  mvP2 2  mvE2   300 kg 1, 20 m/s 
2
2
2
K P  216 N
b) A figura ao lado mostra o esquema de forças que age sobre o pacote
enquanto desliza (acelera) sobre a esteira. Devemos notar que, na vertical
(eixo y), as forças normal (FN) e gravitacional (Fg) anulam-se, ou seja,
possuem módulos iguais e sentidos contrários. Logo:
Fat   FN   Fg   mg   0, 400  300 kg   9,81 m/s2   1177, 2 N
Fat  1,18 kN
(c) A energia fornecida pelo motor (EM) é igual à energia cinética fornecida ao pacote mais a
energia dissipada no atrito entre o pacote e a esteira (trabalho da força de atrito, Wat):
EM  K P  Wat
(1)
O trabalho da força de atrito é dado por:
Wat   Fat  ds
onde ds é um elemento de deslocamento do pacote sobre a esteira. Como a força de atrito é
constante e os vetores Fat e ds possuem mesma direção e mesmo sentido (x), teremos:
Wat   Fat ds cos 0  Fat  dx'  Fat x '
(2)
Na equação acima, substituímos ds por dx’, o que já será explicado. O estudante deve notar que x’
é o deslocamento do pacote sobre a esteira (ou seja, num referencial sobre a esteira), enquanto
derrapa sobre ela, o que causa movimento acelerado do pacote para alcançar a velocidade da própria
esteira.
Para um observador no solo, o pacote parte do repouso e é acelerado no sentido x até alcançar a
velocidade constante da esteira, vE. Como o movimento do pacote ocorre sobre uma superfície em
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
2
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Problemas Resolvidos de Física
movimento, fica mais fácil determinar seu deslocamento (x’) a partir de um referencial inercial
fixo sobre a esteira (referencial x’y’, daí a substituição de ds por dx’). Nesse referencial, um
observador veria o pacote com velocidade inicial v0x’ = vP’ = 1,20 m/s no sentido +x’, sendo
desacelerado pela força de atrito Fat na direção x’. Ao término do deslizamento do pacote, este
estará em repouso sobre a esteira.
Cálculo de x’ (movimento acelerado):
vx2'  v02x '  2ax '  x'  x0' 
0  vP'  2aP' x'
x '  
vP'2
2aP'
(3)
Cálculo da aceleração do pacote:
F
x'
 max '
 Fat  maP'
Fat
m
Substituindo-se (4) em (3), teremos:
aP'  
(4)
mv 2  300 kg 1, 20 m/s 
x  P 
 0,183486
2 Fat
2 1177, 2 N 
2
'
m
Substituindo-se este valor em (2), teremos:
Wat  1177, 2 N  0,183486
m   216 J
Agora podemos calcular a energia fornecida pelo motor substituindo-se os valores numéricos
apropriados na Eq. (1):
EM  K P  Wat   216 N    216 N 
EM  512 N
d) EM e KP são diferentes (EM  KP) porque o motor precisa fornecer mais energia do que o valor da
energia cinética final do pacote por causa da perda de energia devida ao atrito entre o pacote e a
esteira.
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
3