Teorema de Tales - profmariocastro

Teorema de Tales
O Teorema de Tales possui diversas aplicações no cotidiano, que devem ser
demonstradas a fim de verificar sua importância. O Teorema diz que “retas
paralelas, cortadas por transversais, formam segmentos correspondentes
proporcionais”.
Algumas considerações preliminares
O enunciado do Teorema de Tales será compreensível a partir da
consideração, nesse primeiro momento, de alguns elementos básicos: um feixe
de retas paralelas r, s e t que cortam as retas transversais u e v.
Neste exemplo, o feixe de retas é formado por apenas três retas paralelas e
duas transversais, mas outros feixes podem ser formados com maior número
de retas paralelas contidas num mesmo plano.
No feixe acima, destacam-se os seguintes elementos:

Pontos correspondentes: A e D, B e E, C e F;

Segmentos correspondentes: AB e DE, BC e EF, AC e DF.
O teorema de Tales:
“Se duas retas transversais são cortadas por um feixe de retas paralelas, então
a razão entre quaisquer dos segmentos determinados em uma das transversais
é igual à razão entre os segmentos correspondentes da outra transversal.”
No feixe de retas exemplificado anteriormente, podemos destacar, de acordo
com o Teorema de Tales, as seguintes razões:
Aplicação do teorema
c) Fuvest–SP) Três terrenos têm frente para a rua A e para a rua B, como na
figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente
para a rua B de cada lote, sabendo que a frente total para essa rua tem 180m?
Com base no enunciado, vamos fazer umas anotações na imagem.
ATIVIDADES
1) Determine o valor de x, y e z em cada uma das figuras:
a)
b)
c)
d)
e)
f)
2) Ao realizar a instalação elétrica de um edifício, um eletricista observou
que os dois fios r e s eram transversais aos fios da rede central
demonstrados por a, b, c, d. Sabendo disso, calcule o comprimento x e y
da figura.
Obs.: os fios da rede central são paralelos.
3) No triângulo ABC da figura abaixo temos que DE//BC Sabendo que a
medida do lado BC do triângulo é 14 cm, calcule as medidas dos
lados AB e AC o perímetro desse triângulo.
4) No triângulo da figura abaixo, as medidas são consideradas em
centímetros. Se BC=32 cm, calcule o valor de x – y.
5) No triângulo ABC a seguir, o segmento DE é paralelo ao segmento BC.
Determine o valor de x aplicando a proporcionalidade entre segmentos
paralelos cortados por segmentos transversais.
6) Observe a figura r // s // t. Calcule o valor de x de acordo com o Teorema
de Tales.
7) Nas figuras, a//b//c, calcule o valor de x:
a)
b)
c)
d)
e)
f)
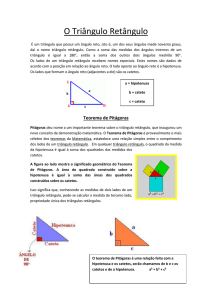
Teorema de Pitágoras
Considerado um dos mais importantes teoremas da Matemática, o
Teorema de Pitágoras foi desenvolvido por Pitágoras de Samos, filósofo grego
que viveu no séc. VI a.C., fundador da mística Escola Pitágorica.
O Teorema de Pitágoras pode ser aplicado em qualquer triângulo
retângulo no intuito de determinar uma das medidas quando conhecidas as
outras duas. O Teorema não se restringiu somente ao triângulo retângulo, de
acordo com estudos da época, eram conhecidos os números inteiros e as
frações, sendo através das aplicações do Teorema iniciado o estudo dos
números irracionais.
O Teorema consistia na seguinte relação:
“A medida do quadrado da hipotenusa é igual à soma das medidas dos
quadrados dos catetos”
Exemplos
1 – Determine a medida da hipotenusa do triângulo representado pela figura a
seguir:
2 – Dado o triângulo retângulo a seguir, determine a medida do cateto y.
3) Calcule a altura do muro x:
4) Encontre o valor de c:
ATIVIDADES
1) Usando o teorema de Pitágoras encontre o valor de x nas seguintes figuras:
a)
b)
c)
d)
2) Um avião percorreu a distância de 5 000 metros na posição inclinada, e em
relação ao solo, percorreu 3 000 metros. Determine a altura do avião.
3) Do topo de uma torre, três cabos de aço estão ligados à superfície por meio
de ganchos, dando sustentabilidade à torre. Sabendo que a medida de cada
cabo é de 30 metros e que a distância dos ganchos até à base da torre é de
15 metros, determine a medida de sua altura.
4) Calcule a metragem de arame utilizado para cercar um terreno triangular com
as medidas perpendiculares de 60 e 80 metros, considerando que a cerca de
arame terá 4 fios.
Lista 2
LISTA 3
Razões trigonométricas
Catetos e Hipotenusa
Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os
lados adjacentes de catetos.
Observe a figura:
HIPOTENUSA: BC
CATETOS: AC E AB
Seno, Cosseno e Tangente
Considere um triângulo retângulo BAC:
Hipotenusa:
, m(
) = a.
Catetos:
, m(
) = b.
Ângulos:
, m(
) = c.
, e .

Seno de um ângulo agudo é a razão entre a medida do cateto oposto a
esse ângulo e a medida da hipotenusa.
Assim:

Cosseno de um ângulo agudo é a razão entre a medida do cateto
adjacente a esse ângulo e a medida da hipotenusa.
Assim:

Tangente de um ângulo agudo é a razão entre a medida do cateto
oposto e a medida do cateto adjacente a esse ângulo.
Assim:
Exemplo:
Observações:
1. A tangente de um ângulo agudo pode ser definida como a razão entre
seno deste ângulo e o seu cosseno.
Assim:
2. A tangente de um ângulo agudo é um número real positivo.
3. O seno e o cosseno de um ângulo agudo são sempre números reais
positivos menores que 1, pois qualquer cateto é sempre menor que a
hipotenusa.
SENO, COSSENO E TANGENTE DE 30º, 45º E 60º
x
sen x
cos x
1
0
30º
45º
60º
90º
tg x
Matemática
4º BIMESTRE
8ª série
Aluno:
Turma: