Profª. Drª Maria Lúcia Pereira Antunes
ENGENHOCAS
LANÇAMENTO DE FOGUETE DE GARRAFA
PET
Henrique Tavela
Willgner Santos
Sorocaba
2015
I.
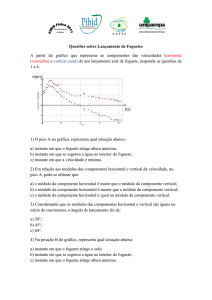
OBJETIVOS
O principal objetivo deste experimento foi provar que o lançamento obliquo
de garrafa pet, cheia com água, não descreve um movimento em duas dimensões
completo.
II.
INTRODUÇÃO
Primeiramente devemos compreender como se dá estabilidade do vôo para
isso devemos encontrar o Centro de Massa (CM) que é encontrado ou tentando
equilibrar a garrafa sobre uma régua ou a partir da equação 1.
(1)
E também devemos encontrar o Centro de Pressão (CP), responsável pela
influência da força aerodinâmicas do sistema, que é a média da somas das áreas
do corpo, que é dado pela equação 2.
(2)
Assim para termos uma boa estabilidade o CM deve ficar até 1,5 cm acima
do CP, para que possa haver correção por parte do CP se a garrafa sair do eixo, se
o CP estiver acima é ruim pois se a garrafa sair do eixo o CP irá aumentar o desvio
dele e não subirá bem, podemos analisar isto através da Figura 1.
Figura 1
Assim temos a estabilidade do corpo durante seu vôo, depois devemos
compreender como que ocorre a propulsão do foguete que é dada pelo Empuxo e
pelas leis de Newton.
Pela 1ª Lei de Newton temos A Lei da Inércia diz que "Qualquer corpo em
movimento continuará se movendo e qualquer corpo parado permanecerá parado
até que alguma força externa aja sobre ele". Em outras palavras, inércia é a
tendência que os objetos têm de resistir a mudanças no movimento. Ela tem a ver
com a massa do objeto, que no cotidiano costumamos de chamar de peso.
Figura 2: Uma garrafa mais cheia tem mais inércia, pois
mais massa. Mais inércia quer dizer mais resistência a
mudanças de direção. O vento precisa trabalhar mais para
alterar o curso da garrafa.
Figura 3: Uma garrafa menos cheia tem menos inércia,
pois possui menos massa. Menos inércia quer dizer menos
resistência a mudanças de direção. Com pouca força o vento
empurra a garrafa para outro curso.
Pela Segunda Lei de Newton diz que a Força aplicada é igual à massa vezes a
aceleração, ou: F=m·a (3). Se dois foguetes aplicam forças iguais.
Figura 4: Uma garrafa de maior massa (mais cheia) terá uma
menor aceleração.
Figura 5: Uma garrafa de menor massa (menos
cheia) terá uma maior aceleração.
E pela Terceira Lei de Newton diz que "para cada ação, há uma reação de
igual intensidade e de sentido oposto". Isso quer dizer que quanto mais água for
expelida e quanto mais depressa isso acontecer, maior será a reação da garrafa,
assim pela conservação da quantidade de movimento essa reação proporcionará o
foguete para cima.
Massa da garrafa e da água X Velocidade da garrafa
É IGUAL A
Massa da água espelida X Velocidade da água expelida
O empuxo é como chamamos a força que faz subir o foguete.
Nos foguetes a água, o ar pressurizado empurra a água para fora, causando uma
reação da garrafa em sentido oposto (3ª Lei de Newton).
Portanto o empuxo depende tanto da velocidade com que a água é expelida
quanto do "tamanho" do bocal de saída. Assim, o empuxo pode ser calculado como
sendo aproximadamente igual ao dobro do produto da pressão pela área da seção
do bocal. Ou seja, E = 2·P·A (4).
Assim de maneira simplificada o aluno pode ver vários conceitos vistos em
sala de aula em pratica neste experimento.
Já para o Ensino Superior podemos dar uma explicação mais detalhada e
usando equações mais elaboradas como será descrito a partir de agora. Para o
calculo do CM e CP serão usados as mesma equações usadas no Ensino Médio, e
para descrever o movimento do foguete durante a ejeção de água vamos usar uma
aplicação da segunda Lei de Newton.
Para sua descrição, consideremos que a única força atuante sobre o foguete
é a força gravitacional (desprezemos o atrito do ar). Imaginemos que o foguete está
em movimento inicial uniforme, com velocidade constante v. Na realidade a
velocidade é zero, pois o foguete está parado sobre a base de lançamentos, mas
utilizaremos este artifício para manipulações matemáticas mais simples. O
momento linear inicial do foguete será então pi = Mv, onde M é sua massa inicial
que é dada por M=mF +mH2O, ou seja, a massa do foguete vazio (mF) mais a
massa de água contida em seu interior (mH2O). No momento em que ocorre a
ejeção de uma pequena quantidade de água ∆mH2O a uma velocidade vf , a
velocidade do foguete é alterada de ∆v. Logo, o sistema terá um momento final
dado por:
Se ΣF = -Mg, substituindo a Eq. (6) na Eq. (5)
Manipulando esta equação e desprezando o termo ∆mH2O∆v já que ∆mH2O
é muito pequeno, obtemos para a velocidade do foguete ∆v:
Onde u é a velocidade de escape da água relativa ao foguete, u = v + vf .
Utilizando as quantidades ∆mH2O = ρ∆V e M = ρVH2O + mF, onde ρ é a densidade
da água, ∆V a mudança no volume de ar dentro do foguete, VH2O o volume de
água dentro do foguete e mF a massa do foguete vazio, temos:
Podemos obter a velocidade do foguete durante o tempo ∆t de ejeção da
água conhecendo-se a velocidade de escape da água u em relação ao foguete.
(a)Configuração do foguete no momento em que não é ejetada nenhuma
quantidade de água, sua massa é M e sua velocidade é v. A única força atuante é a
força gravitacional. (b) Configuração do foguete após a ejeção de uma pequena
quantidade de água com massa ∆m h 20 e a velocidade vf. A massa do foguete
muda para M-∆m h 20 e sua velocidade para v+∆v. (c) Mostra-se o volume V de
ar dentro do foguete; P, a pressão sobre a superfície da água; Df o diâmetro do
foguete; Db o diâmetro do bocal; ρ, a densidade da água; Vl, a velocidade da água
dentro do foguete; u, a velocidade de escape da agua em relação ao foguete e P
atm , a pressão atmosférica.
Para obtermos u, vamos considerar a água como um fluido perfeito e
incompressível e seu escoamento pelo tubo (foguete) estacionário. Utilizando a
equação de Bernoulli, temos:
Onde as quantidades apontadas no primeiro membro da Eq. (10) estão
relacionadas à quantidade de água no interior do foguete, ou seja, sua densidade ρ
e sua velocidade vL, a pressão P em sua superfície. No segundo membro estão as
quantidades relacionadas à porção de água que é ejetada do foguete, que são sua
velocidade relativa u, a qual queremos encontrar, e a pressão atmosférica Patm no
bocal da garrafa. Note que estamos desprezando a parte da energia potencial
gravitacional da equação de Bernoulli, pois sua magnitude é desprezível
comparada com as outras grandezas envolvidas [7]. Ambas as velocidades u e vL
estão relacionadas com a taxa com que a água é ejetada, ou, equivalentemente, à
taxa com que o volume de ar V dentro da câmara aumenta. Esta relação é dada
pela equação de continuidade:
Sendo DB e DF os diâmetros do bocal e do corpo da garrafa,
respectivamente. A Fig. 14c ilustra as grandezas apresentadas nas Eqs. (10) e (11).
Da Eq. (11) observa-se que vL é proporcional à razão DB/DF, que por sua
vez é muito menor que 1, tornando-se menor ainda quando elevada à quarta
potência na Eq. (10). Logo, podemos desprezar o primeiro termo da Eq. (10), o que
nos permite obter a expressão para a velocidade de escape da água, que é dada
por:
Quando a garrafa retorna ao solo observa-se que há vapor de água dentro
da mesma, e isso implica que houve resfriamento do ar dentro da garrafa no
momento de sua expansão. Como ∆t é muito pequeno, significa que este processo
de expansão pode ter ocorrido sem trocas de calor entre o sistema, câmara de
compressão e a vizinhança. Portanto podemos supor que houve uma expansão
adiabática. Admitindo que o ar seja um gás ideal, temos:
(eq.13)
Onde P0 é a pressão absoluta inicial dentro do foguete, V0 o volume inicial
de ar dentro do mesmo e V seu volume final, que é o volume da garrafa. Como o ar
pode ser considerado um gás diatômico, temos que γ = 1,4. Substituindo a Eq. (13)
na Eq. (12), obtemos finalmente, para a velocidade de escape da água.
Onde uC é a velocidade característica dada por:
Calculando u pela Eq. (14) e substituindo na Eq. (8), pode-se obter a
velocidade do foguete no momento em que ocorre toda ejeção de água (Eq. (16)) e
estimar sua aceleração durante o processo que, dependendo da pressão imposta,
pode ser da ordem de dezenas de vezes a aceleração da gravidade; um resultado
realmente incrível utilizando apenas garrafas PET, água e ar comprimido.
Desta forma encerramos a descrição do movimento do foguete, lembrando
que após ele atingir sua velocidade máxima ele começara a desacelerar e depois a
cair em queda livre seguindo a equação da velocidade:
V = V0 - gt (17)
Sendo que o V0 será dado pela Eq (16), até quando V=0 que é onde ele
começara a cair e acelerar com a gravidade até atingir o solo. Onde podemos
calcular a altura aproximada obtida medindo o tempo de queda e aplicando na
equação [7]:
Onde H = gt2 (18), 2 onde H é a altura, o tempo t será medido e g é a
gravidade. (1)
As equações necessárias para se estudar um lançamento em duas
dimensões são separadas nos eixos X e Y, as equaçoes pertencentes ao estudo do
eixo X sao:
X=
Vx*t, onde Vx é a velocidade na direçao X e t o tempo(19)
A= (V02*sen2θ)/g(20), onde A é o alcance na horizontal
Vx=V0*senθ(21), Vo a velocidade inicial e o senθ o ângulo de inclinaçao.
E as equaçoes para estudar o movimento no eixo Y são:
Y=V0y t+(gt2)/2(22), onde g é a gravidade
Vy = V0y +gt(23)
Vy2= V0y + 2gy(24)
H= ( V0*senθ)2/2g(25), onde H é altura maxima atingida.
MATERIAIS E MÉTODOS
III.
Os materiais usados para a realização deste experimento foram:
2 T’s de ¾
3 cotovelos de ¾ de 90º
8 pedaços de cano pvc de ¾ de 12 cm cada
1 pedaço de ½ de 17 cm
1,30 m de mangueira de nível
1 bico de câmara de pneu de bicicleta
1 braçadeira
1 garrafa pet
Fita adesiva
Veda rosca
Martelo
Adaptador para encaixar melhor os canos ½ com o ¾
Silicone
Bomba de encher pneu de bicicleta
MÉTODOS
Primeiramente, foi construído a plataforma de lançamento do foguete de
garrafa PET, para isso usou-se os materiais a cima citados. Para começar, é
necessário encaixar os canos de pvc, usando os tampões de um lado e do outro
lado o cotovelo ¾ para que fiquem dessa forma:
Fazer isso mais duas vezes para que se tenha os três pés da plataforma.
Após ter feito o passo a cima use um T para juntar dois canos e o outro T na
extremidade do cano que ainda não foi usado, de modo que os T’s fiquem
perpendiculares. Deverá ficar desse jeito.
Com os três conectados através dos T’s, use o adaptador e encaixe o cano
mais fino(½) no mais largo(¾), para vedar é aconselhável que se use a veda rosca,
com todos os canos encaixados fure um T para que se possa passar a mangueira
de nível por dentro dos canos. De modo que fique assim:
Após ter passado a mangueira, use bastante silicone, para obter a maior
vedação possível. O próximo passo é passar veda rosca no cano mais fino no
altura que desejar, para que a garrafa PET encaixe bem no cano e assim gerando
pressão ao bombear ar para dentro da garrafa.
Agora, deve-se terminar o trabalho do outro lado da mangueira, para isso
deve-se pegar o bico da câmara de pneu de bicicleta e encaixar na mangueira para
que se firma bem e vede bem, é necessário usar a braçadeira, veda rosca e, se
necessário, a fita adesiva.
Para acabar o sistema de bombeamento, encaixe a bomba de ar no bico da
câmara.
Após fazer os passos a cima, nosso sistema ficou dessa maneira:
IV.
RESULTADOS
Pode-se perceber que a trajetória descrita pelo nosso foguete foi em duas
dimensões (x e y), ou lançamento oblíquo, a direção x descreve um movimento
uniformemente variado, onde a força que atrapalha o deslocamento é a força de
arrasto. E na direção y o movimento feito é o movimento uniformemente variado
onde a força que atrapalha o deslocamento é a própria gravidade.
Durante a realização do nosso experimento nosso projétil foi lançado cerca
de 15 metros de distância e cerca de 4 metros de altura, pode-se perceber que ao
longo da trajetória descrita pelo foguete montado com garrafa PET quando atinge
um certo ponto despenca ao chão, isso ocorre devido a alguns fatores que serão
explicados na conclusão.
Pode-se perceber também que a aerodinâmica do nosso foguete não é muito
boa, isso pode ser melhorado com alguns ajustes, como aumento de peso da
garrafa, melhorar a infraestrutura do foguete, colocando asas entre outras coisas,
como o nosso foguete não possui uma aerodinâmica boa a força de arrasto que
atua sobre o nosso corpo é maior, fazendo com que a garrafa gire e perca
parcialmente o rumo da trajetória.
V.
CONCLUSÃO
Após a realização deste experimento pode-se concluir que o
lançamento de foguete de garrafa PET não realiza um movimento obliquo
completo, isso ocorre, pois, diferente dos lançamentos oblíquos
estudados em sala em que o corpo é um corpo rígido com massa fixa,
nosso corpo de experimento sofria variação da massa, a partir do
momento que o foguete decolava ele perdia água, e também sofria
variação de pressão, o que fazia com que o foguete decolasse até uma
certa altura e distância, e no ponto em que o foguete não possuía mais
massa(água), nem pressão interna, despencasse ao chão.
A seguir há um anexo que visa explicar a trajetória percorrida pelo
nosso foguete.
VI.
ANEXOS
(2)
VII.
REFERÊNCIAS BIBLIOGRÁFICAS
(1) Disponível em: <
http://www.ifi.unicamp.br/~lunazzi/F530_F590_F690_F809_F895/F809/F8
09_sem2_2009/LucasC_Luengo_RF2.pdf>. Data de acesso: 19/06/2015.
(2) Disponível em: < http://www.spacex.com/news/2015/05/04/5-thingsknow-about-spacexs-pad-abort-test>. Data de acesso: 23/06/2015
(3) Disponivel em:<http://www.brasilescola.com/fisica/lancamentoobliquo.htm>. Data de acesso:23/06/2015.