- COC Imperatriz Unidade II

1° ANO E 3° ANO
1. Dois carros, A e B, movem-se no mesmo sentido, em uma estrada reta, com
velocidades constantes VA = 100 km/h e VB = 80 km/h, respectivamente.
a) Qual é, em módulo, a velocidade do carro B em relação a um observador no carro
A?
b) Em um dado instante, o carro B está 600 m à frente do carro A. Quanto tempo, em
horas, decorre até que A alcance B?
2. Uma criança solta uma pedrinha de massa m = 50 g, com velocidade inicial nula, do
alto de um prédio de 100 m de altura. Devido ao atrito com o ar, o gráfico da posição
da pedrinha em função do tempo não é mais a parábola y = 100 - 5t2, mas sim o
gráfico representado adiante.
a) Com que velocidade a pedrinha bate no chão (altura = 0)?
b) Qual é o trabalho realizado pela força de atrito entre t = 0 e t = 11 segundos?
3. Um velocista consegue fazer os 100 metros finais de uma corrida em 10 segundos.
Se, durante esse tempo, ele deu passadas constantes de 2,0 metros, qual foi a
frequência de suas passadas em hertz?
4. Num caminhão-tanque em movimento, uma torneira mal fechada goteja à razão de
2 gotas por segundo. Determine a velocidade do caminhão, sabendo que a distância
entre marcas sucessivas deixadas pelas gotas no asfalto é de 2,5 metros.
5. Um atleta que se preparou para participar das Olimpíadas de Atlanta corre a prova
dos 100 metros rasos em apenas 9,6 segundos. Calcule sua velocidade média.
6. Um professor de física utiliza um cronômetro para medir em quanto tempo uma
moeda cai de uma altura de um metro e vinte centímetros no interior de um elevador.
Com o elevador parado o tempo medido foi meio segundo cravado. Se a medida for
realizada com o elevador subindo em movimento uniforme o tempo será maior, menor
ou o mesmo?
7. Como se deve mover um corpo de maneira que sua velocidade vetorial permaneça
CONSTANTE?
8. Em uma estrada o limite de velocidade é de 100 km/h. Poderá ser multado um carro
que esteja viajando a 30 m/s?
9. Qual a velocidade média de um atleta que faz 50 m em 4,0 s?
10. A equação horária S = 3 + 4 . t, em unidades do sistema internacional, traduz, em
um dado referencial, o movimento de uma partícula. No instante t = 3 s, qual a
velocidade da partícula?
11. Um trem de 200 m de comprimento viaja a 10 m/s. Qual o intervalo de tempo
necessário para que este trem ultrapasse um poste que está ao lado da linha férrea?
12. Um trem de 200 m de comprimento viaja a 20 m/s. Qual o intervalo de tempo
necessário para que este trem ultrapasse um túnel de 300 m de comprimento?
13. Um corpo é abandonado da altura de 45 m. Determine o intervalo de tempo
necessário entre o momento em que o corpo é abandonado e o instante em que ele
chega ao solo.
14. Admitindo que um circuito tenha 5 km de extensão, e que uma corrida disputada
neste tenha 78 voltas e que a média de velocidade das voltas é de 195 km/h, em
quanto tempo o piloto termina a corrida?
15. Dois carros partem de um mesmo lugar e viajam numa mesma direção e no
mesmo sentido. Um deles faz o percurso com uma velocidade média de 70 km/h e o
outro, com 80 km/h. No fim de 2,5h, qual a distância entre eles?
16. A velocidade média do ultra-som, na água do mar, é de 1500 m/s. O operador do
sonar de um barco pesqueiro observou no aparelho o registro de duas reflexões. A
primeira, 1/4 de segundo após a emissão do ultra-som, era correspondente a um
cardume que passava. A outra, recebida 2 segundos após a emissão, era de próprio
fundo do mar. Com esses dados, responda a que profundidade se encontrava o
cardume e qual a profundidade do fundo do mar no ponto assinalado?
17. Um circuito tem x km de extensão. Uma corrida disputada neste circuito tem 78
voltas, e a velocidade média das voltas é de 195 km/h, em 2 horas de corrida. Qual o
valor de x?
18. Em um trecho em declive, de
velocidade máxima permitida para
leves é de 80 km/h. Suponha que
trecho em declive simultaneamente
estabelecidas.
20 km de extensão, de uma estrada federal, a
veículos pesados é de 70 km/h e para veículos
um caminhão pesado e um automóvel iniciem o
e que mantenham velocidades iguais às máximas
Calcule a distância entre os dois veículos no instante em que o automóvel completa o
trecho em declive.
19. Um maratonista percorre a distância de 42 km em duas horas e quinze minutos.
Determine a velocidade escalar média, em km/h, do atleta ao longo do percurso.
20. Um submarino em combate lança um torpedo na direção de um navio ancorado.
No instante do lançamento o submarino se movia com velocidade v = 14 m/s. O
torpedo é lançado com velocidade v(ts), em relação ao submarino. O intervalo de
tempo do lançamento até a colisão do torpedo com o navio foi de 2,0 min. Supondo
que o torpedo se moveu com velocidade constante, calcule v(ts) em m/s.
21. Um atleta dá 150 passos por minuto, cada passo com um metro de extensão.
Calcule quanto tempo ele gasta, nessa marcha, para percorrer 6,0 km.
22. Um estudante a caminho da UFRJ trafega 8,0 km na Linha Vermelha a 80 km/h
(10 km/h a menos que o limite permitido nessa via).
Se ele fosse insensato e trafegasse a 100 km/h, calcule quantos minutos economizaria
nesse mesmo percurso.
23. Um automóvel faz o percurso Recife-Gravatá a uma velocidade média de 50 km/h.
O retorno, pela mesma estrada, é realizado a uma velocidade média de 80 km/h.
Quanto, em percentual, o tempo gasto na ida é superior ao tempo gasto no retorno?
24. Numa competição, Fernanda nadou 6,0 km e, em seguida, correu outros 6,0 km.
Na etapa de natação, conseguiu uma velocidade escalar média de 4,0 km/h; na
corrida, sua velocidade escalar média foi de 12 km/h.
a) Calcule o tempo gasto por Fernanda para nadar os 6,0 km.
b) Calcule a velocidade escalar média de Fernanda no percurso total da prova.
25. Para se dirigir prudentemente, recomenda-se manter do veículo da frente uma
distância mínima de um carro (4,0 m) para cada 16 km/h. Um carro segue um
caminhão em uma estrada, ambos a 108 km/h.
a) De acordo com a recomendação acima, qual deveria ser a distância mínima
separando os dois veículos?
b) O carro mantém uma separação de apenas 10m quando o motorista do caminhão
freia bruscamente. O motorista do carro demora 0,50 segundo para perceber a freada
e pisar em seu freio. Ambos os veículos percorreriam a mesma distância até parar,
após acionarem os seus freios. Mostre numericamente que a colisão é inevitável.
26. A figura representa o gráfico velocidade × tempo do movimento retilíneo de um
móvel.
a) Qual o deslocamento total desse móvel?
b) Esboce o gráfico posição × tempo correspondente, supondo que o móvel partiu da
origem.
27. A partir da altura de 7 m atira-se uma pequena bola de chumbo verticalmente para
baixo, com velocidade de módulo 2,0 m/s. Despreze a resistência do ar e calcule o
valor, em m/s, da velocidade da bola ao atingir o solo.
28. Um paraquedista, descendo na vertical, deixou cair sua lanterna quando estava a
90 m do solo. A lanterna levou 3 segundos para atingir o solo. Qual era a velocidade
do paraquedista, em m/s, quando a lanterna foi solta?
29. Um avião em movimento solta uma bomba que cai até atingir o solo. Qual a
trajetória da bomba em relação a quem se encontra fora do avião? Despreze a
resistência do ar.
30. Um corpo parte do repouso, acelerado com 2 m/s2. Após percorrer a distância de
16 m, com que velocidade o móvel se encontrará?
31. Um corpo possui velocidade inicial de 8 m/s e desacelera a 2 m/s2. Qual a
distância que o corpo percorre até parar?
32. O que a equação cinemática de Torricelli tem de especial, quando comparada com
as equações cinemáticas de Galileu para o movimento uniformemente acelerado?
33. Qual o tempo necessário para que um corpo que acelera a 2 m/s2, partindo do
repouso, atinja a velocidade de 108 km/h?
34. As faixas de aceleração das auto-estradas devem ser longas o suficiente para
permitir que um carro partindo do repouso atinja a velocidade de 100 km/h em uma
estrada horizontal. Um carro popular é capaz de acelerar de 0 a 100 km/h em 18 s.
Suponha que a aceleração é constante.
a) Qual o valor da aceleração?
b) Qual a distância percorrida em 10 s?
c) Qual deve ser o comprimento mínimo da faixa de aceleração?.
35. Numa competição automobilística, um carro se aproxima de uma curva em grande
velocidade. O piloto, então, pisa o freio durante 4s e consegue reduzir a velocidade do
carro para 30m/s. Durante a freada o carro percorre 160m.
Supondo que os freios imprimam ao carro uma aceleração retardadora constante,
calcule a velocidade do carro no instante em que o piloto pisou o freio.
36. Um veículo em movimento sofre uma desaceleração uniforme em uma pista reta,
até parar. Sabendo-se que, durante os últimos 9,0 m de seu deslocamento, a sua
velocidade diminui 12 m/s, calcule o módulo da desaceleração imposta ao veículo, em
m/s2.
37. Um veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal,
quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz
uniformemente à razão de 4 m/s em cada segundo a partir do momento em que o freio
foi acionado, determine
a) o tempo decorrido entre o instante do acionamento do freio e o instante em que o
veículo pára.
b) a distância percorrida pelo veículo nesse intervalo de tempo.
38. Considere o movimento de um caminhante em linha reta. Este caminhante
percorre os 20,0 s iniciais à velocidade constante v• = 2,0 m/s. Em seguida, ele
percorre os próximos 8,0 s com aceleração constante a = 1 m/s2 (a velocidade inicial é
2,0 m/s). Calcule:
a) a distância percorrida nos 20,0 s iniciais;
b) a distância percorrida nos 28,0 s totais;
c) a velocidade final do caminhante.
39. Uma torneira, situada a uma altura de 1,0 m acima do solo, pinga lentamente à
razão de 3 gotas por minuto.
a) Com que velocidade uma gota atinge o solo?
b) Que intervalo de tempo separa as batidas de duas gotas consecutivas no solo?
Considere para simplificar, g = 10 m/s2.
40. Em vôo horizontal, a 3.000 m de altitude, com a velocidade de 540 km/h, um
bombardeiro deixa cair uma bomba. Esta explode 15 s antes de atingir o solo.
Desprezando a resistência do ar, calcule a velocidade da bomba no momento da
explosão.
2° ANO
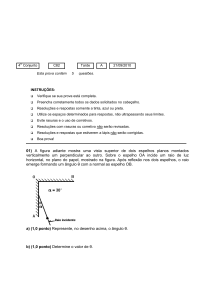
1. A figura adiante representa um objeto A colocado a uma distância de 2,0 m de um
espelho plano S, e uma lâmpada L colocada à distância de 6,0 m do espelho.
a) Desenhe o raio emitido por L e refletido em S que atinge A. Explique a construção.
b) Calcule a distância percorrida por esse raio.
2. Dois espelhos planos e quase paralelos estão separados por 5,0 m. Um homem se
coloca de frente a um dos espelhos, a uma distância de 2,0 m. Ele observa uma
seqüência infinita de imagens, algumas de frente, outras de costas.
a) Faça um esquema mostrando o homem, os espelhos e as quatro primeiras imagens
que o homem vê.
b) Indique no esquema as imagens de frente e de costas com as iniciais F e C.
c) Quais as distâncias entre as imagens consecutivas?
3. Um observador, a 1,0 m de um espelho plano, vê a imagem de um objeto que está
a 6,0 m do espelho. Quando o observador se aproxima 0,5 m do espelho, a quantos
metros do espelho estará a imagem do objeto?
4. O ângulo de incidência, em um espelho plano, é de 30°. Qual o valor do ângulo
formado entre o raio refletido e a superfície do espelho?
5. Um objeto é colocado entre dois espelhos planos, que tem suas faces refletoras se
confrontando. O objeto está a igual distância dos dois espelhos. O ângulo formado
entre os dois espelhos é de 45°. Qual o número de imagens deste objeto que
podemos ver nos dois espelhos?
6. Um corpo encontra-se a 20 cm da superfície refletora de um espelho plano. Qual a
distância entre o corpo e a imagem conjugada por este espelho?
7. Observa-se a imagem de um relógio conjugada por um espelho plano vertical. O
relógio, dada a posição de seus ponteiros, parece indicar 2h. Na verdade que horas
indica o relógio?
8. Um objeto está a 30 cm de um espelho plano vertical. Este espelho é transladado
para uma posição que fica a 50 cm do objeto. Qual foi o deslocamento da imagem
conjugada deste objeto por este espelho?
9. Um espelho convexo é convergente ou divergente?
10. Um estudante veste uma camiseta em cujo peito se lê a inscrição seguinte:
UNESP
a) Reescreva essa inscrição, na forma que sua imagem aparece para o estudante,
quando ele se encontra frente a um espelho plano.
b) Suponha que a inscrição esteja a 70cm do espelho e que cada letra da camiseta
tenha 10cm de altura. Qual a distância entre a inscrição e sua imagem? Qual a altura
de cada letra da imagem?
11. A imagem de um objeto forma-se a 40 cm de um espelho côncavo com distância
focal de 30 cm. A imagem formada situa-se sobre o eixo principal do espelho, é real,
invertida e tem 3 cm de altura.
a) Determine a posição do objeto.
b) Construa o esquema referente à questão representando objeto, imagem, espelho e
raios utilizados e indicando as distâncias envolvidas.
12. O raio de curvatura de um espelho esférico é de 40 cm. Qual o valor da distância
focal?
13. A imagem de um objeto conjugada por um espelho esférico é real, menor e
invertida. O espelho é côncavo ou convexo?
14. A imagem de um objeto conjugada por um espelho esférico é virtual, menor e
direita. O espelho é côncavo ou convexo?
15. A imagem de um objeto conjugada por um espelho esférico é real, maior e
invertida. O espelho é côncavo ou convexo?
16. Um espelho projeta em uma tela a imagem de um objeto. O espelho é côncavo ou
convexo?
17. Um espelho projeta em uma tela a imagem de um objeto. A imagem é direita ou
invertida?
18. Um raio de luz atinge um espelho côncavo paralelamente ao eixo principal do
espelho. Este raio, após se refletir, irá passar pelo centro de curvatura, pelo foco ou
pelo vértice?
19. A imagem de um objeto forma-se a 40 cm de um espelho côncavo com distância
focal de 30 cm. A imagem formada situa-se sobre o eixo principal do espelho, é real,
invertida e tem 3 cm de altura.
a) Determine a posição do objeto.
b) Construa o esquema referente à questão representando objeto, imagem, espelho e
raios utilizados e indicando as distâncias envolvidas.
20. Um objeto O, em forma de seta de 5,0cm de comprimento, está apoiado no eixo
principal de um espelho esférico côncavo de distância focal 40cm, a 50cm do vértice
como está indicado no esquema.
a) Determine a distância da imagem ao vértice do espelho, em cm.
b) Determine o valor do comprimento da imagem, em cm.
21. Na entrada do circo existe um espelho convexo. Uma menina de 1,0m de altura vê
sua imagem refletida quando se encontra a 1,2m do vértice do espelho. A relação
entre os tamanhos da menina e de sua imagem é igual a 4.
Calcule a distância focal do espelho da entrada do circo.
22. Um espelho côncavo tem um raio de curvatura R = 2,0 m. A que distância do
centro do espelho, em centímetros, uma pessoa deve se posicionar sobre o eixo do
espelho para que a ampliação de sua imagem seja A = +2?
23. Para evitar acidentes de trânsito, foram instalados espelhos convexos em alguns
cruzamentos. A experiência não foi bem sucedida porque, como os espelhos convexos
fornecem imagens menores, perde-se completamente a noção de distância. Para
perceber esse efeito, suponha que um objeto linear seja colocado a 30 m de um
espelho convexo de 12 m de raio, perpendicularmente a seu eixo principal.
a) A que distância do espelho convexo seria vista a imagem desse objeto?
b) Se substituíssemos o espelho convexo por um espelho plano, a que distância deste
espelho seria vista a imagem daquele objeto?
24. Com o objetivo de obter mais visibilidade da área interna do supermercado,
facilitando o controle da movimentação de pessoas, são utilizados espelhos esféricos
cuja distância focal em módulo é igual a 25 cm. Um cliente de 1,6 m de altura está a
2,25 m de distância do vértice de um dos espelhos.
a) Indique o tipo de espelho utilizado e a natureza da imagem por ele oferecida.
b) Calcule a altura da imagem do cliente.
25. Uma caixa d'água cilíndrica, com altura h = 36 cm e diâmetro D = 86 cm, está
completamente cheia de água. Uma tampa circular, opaca e plana, com abertura
central de diâmetro d, é colocada sobre a caixa. No esquema a seguir, R representa o
raio da tampa e r o raio de sua abertura.
Determine o menor valor assumido por d para que qualquer raio de luz incidente na
abertura ilumine diretamente o fundo da caixa, sem refletir nas paredes verticais
internas.
26. A figura representa, esquematicamente, a trajetória de um estreito feixe de luz
branca atravessando uma gota d'água. É dessa forma que se origina o arco-íris.
a) Que fenômenos ópticos ocorrem nos pontos 1, 2 e 3?
b) Em que ponto, ou pontos, a luz branca se decompõe, e por que isso ocorre?
27. Um prisma reto de vidro cuja base é um triângulo retângulo isósceles foi totalmente
mergulhado em água. Calcule o menor índice de refração que tal prisma deverá ter,
para que reflita por completo um raio que incida normalmente em uma das faces
menores. Considere que o índice de refração.
28. Na figura a seguir, o semidisco transparente, de centro O, de raio igual a 1,0m,
possui a face curva interna espelhada e ângulo limite de refração igual a 60°.
Um raio de luz incide perpendicularmente à sua face plana, a distância d de seu
centro, é refletido em sua face espelhada e, a seguir, sofre uma reflexão total na face
plana.
A partir desses dados, calcule:
a) o índice de refração do semidisco;
b) a distância d.
29. Uma pequena pedra repousa no fundo de um tanque de x m de profundidade.
Determine o menor raio de uma cobertura circular, plana, paralela à superfície da água
que, flutuando sobre a superfície da água diretamente acima da pedra, impeça
completamente a visão desta por um observador ao lado do tanque, cuja vista se
encontra no nível da água. Justifique.
Dado: índice de refração da água n = (4/3)
30. Em meados do século XX, pesquisadores começaram a sugerir a utilização de
guias para conduzir a luz. Em 1970, isto foi conseguido com um fio muito fino de fibra
de vidro (núcleo) revestido por outro material, escolhido de modo a permitir que a luz
fosse totalmente refletida ao longo do fio. Desta forma, obteve-se o que atualmente é
conhecido como fibra óptica.
Suponha que um feixe LASER penetre no núcleo de uma fibra óptica a partir do ar,
fazendo um ângulo α com seu eixo, como indicado na figura.
Dados:
Índice de refração do revestimento = 1,52
Índice de refração do vidro = 1,60
Índice de refração do ar = 1,00
Calcule o maior valor de α que possibilita a propagação do feixe ao longo da fibra.