E v

Viscosidade
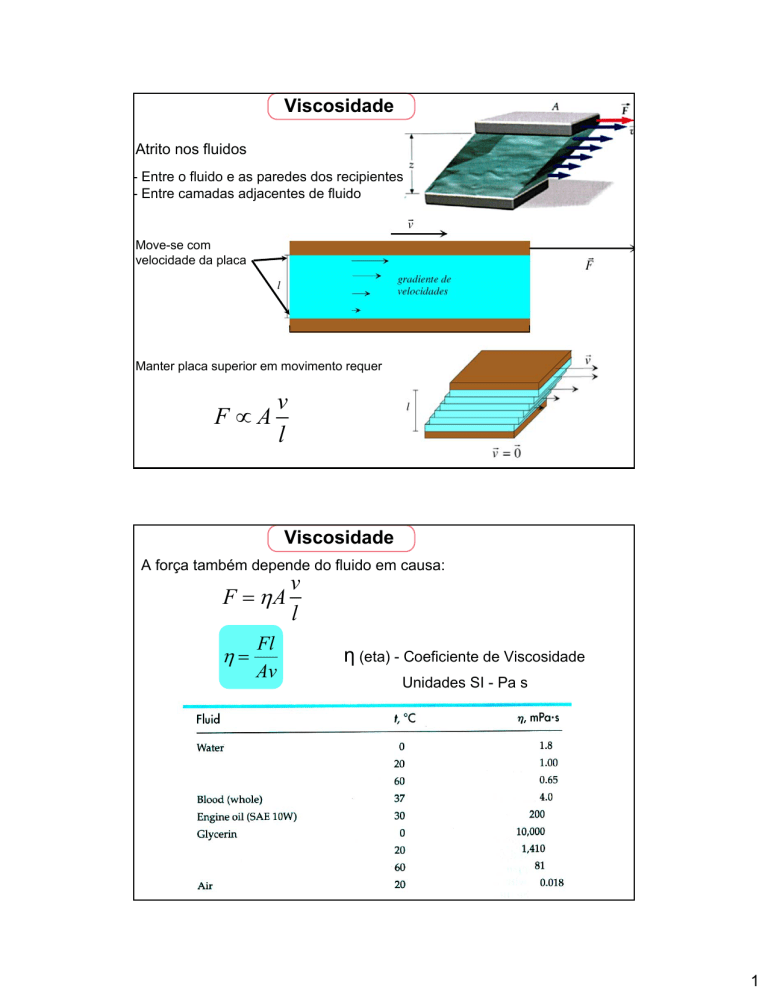
Atrito nos fluidos
- Entre o fluido e as paredes dos recipientes
- Entre camadas adjacentes de fluido
Move-se com
velocidade da placa
Manter placa superior em movimento requer
F∝A
v
l
Viscosidade
A força também depende do fluido em causa:
F = ηA
η=
Fl
Av
v
l
η (eta) - Coeficiente de Viscosidade
Unidades SI - Pa s
1
Viscosidade
Viscosidade
depende de
não depende de
Temperatura
Pressão
Fluido Newtoniano:
Fluido Não-Newtoniano:
velocidade
ou outros
Temperatura
Pressão
velocidade
etc.
Distinção mais formal envolve a relação entre a
força e a variação de velocidade
Newtoniano
Não-Newtoniano
a) variação de velocidade com altura (gradiente) = constante
dv v0
=
dz l
v=
v0
z
l
b) viscosidade depende da forma do gradiente de velocidades
dv
= f (z, v0 , η,l )
dz
2
Escoamento em regime laminar
F = ηA
v
l
Força que lâmina, de área A, exerce na adjacente
F = ηA
dv
dz
Lei de Newton para fluidos
viscosos em regime laminar
Escoamento Viscoso em tubos cilindricos
Fluido não viscoso
Fluido viscoso
velocidade à distância r do eixo
v=
∆PR
4η L
2
⎛
r ⎞
1
−
⎜⎝
R 2 ⎟⎠
2
r=R
r=0
v=0
vmax
∆PR 2
=
4η L
3
Lei de Poiseuille
Resistência ao escoamento em regime laminar
Qv
Entre 1 e 2 escoa-se fluido, de viscosidade η, devido à diferença de
pressão: ∆P = P − P
1
2
∆P = ξQv
Experimentalmente
( V = RI )
Lei de Poiseuille
∆P = ξQv
π R 4 ∆P
Qv =
8η L
Poiseuille
Se η ou L aumentarem
Dependência em
R4
R→
Qv
diminui
R
Q
⇒ Qv → v
2
16
4
Lei de Poiseuille
De
∆ P = ξ Qν
e
ξ=
Qv = Avm = π R vm
2
Qν =
π R 4 ∆P
8η L
8η L
π R4
∆P R 2 vmax
vm =
=
8η L
2
Transição de regime laminar para turbulento
Quando velocidade do fluido passa um valor crítico
Fluxo laminar
Fluxo turbulento
5
Número de Reynolds
Definição:
NR =
2Rρ v
η
Qv = Avm
v é a velocidade média
Dados experimentais:
Fluxo laminar
Fluxo turbulento
N R < 2000
N R > 3000
Ex. Sangue na aorta:
R = 1 cm; v = 0, 3 m s −1 ; ρ = 1060 kg m −3 ; η = 4mPa s
N R = 1590
Viscosidade
F = ηA
dv
dz
Fluido Newtoniano:
dv v0
=
dz l
Lei de Newton para fluidos
viscosos em regime laminar
Fluido Não-Newtoniano:
dv
= f (z, v0 , η,l )
dz
6
Lei de Poiseuille
π R 4 ∆P
Qv =
8η L
Velocidade média do fluido
∆P R 2 vmax
vm =
=
8η L
2
Efeito da Temperatura sobre a Viscosidade
Para a maioria das substâncias:
Ev
A
k
η = Ae
−
Ev
kT
- Energia de activação para fluxo viscoso
- depende do peso e volume molecular
- constante de Boltzmann
7
Efeito da Temperatura sobre a Viscosidade
η = Ae
−
Ev
kT
Fluidos não-Newtonianos
F = ηA
dv
dz
Fluidos Newtonianos:
Para um mesmo z:
F = ηA
v=
v∝F
v
z
z
F
ηA
8
Fluidos não-Newtonianos
INDEPENDENTES DO TEMPO
Fluidos Plásticos:
F = ηA
dv
dz
Viscosidade proporcional à velocidade
após o limite de escoamento
Exs.
- pasta de dentes
- cremes cosméticos
- pasta de tomate
- gorduras
Fluidos não-Newtonianos
INDEPENDENTES DO TEMPO
Fluidos Pseudo-Plásticos:
viscosidade diminui com velocidade
Exs.
- algumas tintas
- shampoo
- pasta de cimento
- concentrados de
sumos de frutas
- ketchup
9
Fluidos não-Newtonianos
INDEPENDENTES DO TEMPO
Fluidos Dilatantes:
viscosidade aumenta com velocidade
Exs.
- areias movediças
- suspensão
concentrada de farinha
Fluidos não-Newtonianos
DEPENDENTES DO TEMPO
Fluidos Tixotrópicos:
viscosidade diminui com o tempo
Exs.
- iogurte
- algumas tintas
- indústria química
- indústria alimentar
10
Fluidos não-Newtonianos
DEPENDENTES DO TEMPO
Fluidos Reopécticos:
viscosidade aumenta com o tempo
Exs.
- pasta de gesso
QuickTime™ and a
Microsoft Video 1 decompressor
are needed to see this picture.
Tipos de Fluidos
Newtoniano
v∝F
⎧
⎧Plástico
⎪
⎪
Independente
do
tempo
⎨Pseudo-plástico
⎪
⎪
⎪Dilatante
Não-Newtoniano ⎨
⎩
⎪
Tixotrópico
⎪Dependente do tempo ⎧⎨
⎪⎩
⎩Reopéctico
11
Medição da Viscosidade
Viscosímetros Cinemáticos
- baseiam-se na Lei de Poiseuille
- método relativo
- só para líquidos Newtonianos
π R 4 ∆P
Qv =
8η L
Viscosímetros Dinâmicos
- determinaçõa de valores absolutos de η
- permite determinar η em função da velocidade
- para qualquer líquido (incluindo não-Newtonianos)
Medição da Viscosidade
Viscosímetros Cinemáticos
π R 4 ∆P
Qv =
8η L
- baseiam-se na Lei de Poiseuille
- método relativo
- só para líquidos Newtonianos
η=
π R 4 ∆P
8LQv
Para um determinado instrumento - mesmo capilar, mesmo volume:
1
t
∝
Qv v
como
∆P ∝ ρ
η∝
π R 4 ∆P t
8Lv
η = kρ t
η = k∆P t
com:
k∝
π R4
8Lv
12
Medição da Viscosidade
Viscosímetros Cinemáticos
η = k∆P t
η1 = k ρ1 t1
Líquido 1:
Líquido 2 - água:
η2 = k ρ 2 t 2
η1 = η2
ρ1 t1
ρ2 t 2
Medição da Viscosidade
Viscosímetros Cinemáticos - Visc. de Ostwald
Variantes:
Cannon-Fenske
Ubbelohde
13
Medição da Viscosidade
Viscosímetros Cinemáticos - Visc. de Hoppler
Força de atrito viscoso na esfera
(Lei de Stokes)
F = 6π η R v
F
I
Força total:
P − I − F = ma
Velocidade terminal (a=0)
F = P−I
P
6π η R vt = (m − V ρliq )g
η=
(m − V ρliq )g
6π R vt
η=
(m − V ρliq )g t
6π R
l
Tipos de Fluidos
Newtoniano
v∝F
⎧
⎧Plástico
⎪
⎪
Independente
do
tempo
⎨Pseudo-plástico
⎪
⎪
⎪Dilatante
Não-Newtoniano ⎨
⎩
⎪
Tixotrópico
⎪Dependente do tempo ⎧⎨
⎪⎩
⎩Reopéctico
14
Medição da Viscosidade
Viscosímetros Cinemáticos
- baseiam-se na Lei de Poiseuille
- método relativo
- só para líquidos Newtonianos
ρ1 t1
η1 = η2
ρ2 t 2
Medição da Viscosidade
Viscosímetros Dinâmicos
- determinação de valores absolutos de η
- permite determinar η em função da velocidade
- para qualquer líquido (incluindo não-Newtonianos)
15
Medição da Viscosidade
Viscosímetros Dinâmicos
Copo e cilindro
Medição da Viscosidade
Viscosímetros Dinâmicos
Brookfield (de vara)
— e - muito grande
— medidas relativas rápidas
16
Medição da Viscosidade
Viscosímetros Dinâmicos
Couette
Medição da Viscosidade
Viscosímetros Dinâmicos
Prato e cone-prato
17
Resistência ao deslocamento num fluido
Fd
viscosa é
∝
v
v
2
para velocidades pequenas
grandes
Velocidades pequenas
Corpo: esfera de raio R e velocidade v
Fluido: viscosidade η e densidade
ρ0
Φ - factor Geométrico
Fd = Φ Rη v
Fd - não depende de ρ 0 pois a
força viscosa também não
Resistência ao deslocamento num fluido
Fd = Φ R η v
Válida se v é muito pequeno
NR =
2 ρ0 v R
η
<1
Muito abaixo do limiar de turbulência (Nr=2000)
Por ex. esfera de r=1cm, Nr<1 se v<1mm/s
Para uma esfera Φ=2π e temos a LEI DE STOKES
Fd = 6π η R v
18
Resistência ao deslocamento num fluido
Velocidade terminal de esfera a cair num fluido:
4
V = π R3
3
W = ρ gV
Fd =W − B
I = B = ρ0 g V
4
4
6 π Rη vt = π R 3 ρ g − π R 3 ρ 0 g
3
3
2R 2
vt =
g( ρ − ρ0 )
9η
Resistência ao deslocamento num fluido
Velocidades elevadas
NR =
ρ0 v R
≥1
η
Fd ∝ v 2
Fd = A C D
ρ0
2
v2
Aplicável a todos os corpos
macroscópicos em qualquer
fluido.
19
Resistência ao deslocamento num fluido
Fd = C D A
ρ0 v 2
2
C D - coeficiente de atrito viscoso (experimental)
A = π R 2 - é a área eficaz
ρ0 v2
- energia cinética por unidade de volume
2
do fluido com velocidade v
Notar que η não aparece – este atrito resulta da aceleração que
o fluido sofre ao mover-se à volta do objecto.
Resistência ao deslocamento num fluido
Fd = C D A
ρ0 v 2
2
-Válido para qualquer objecto e de qualquer forma
-Velocidade terminal: objecto de secção A, comprimento L e
massa ρAL
vt =
(ρ − ρ0 ) 2 g L
ρ0
CD
20
Resistência ao deslocamento num fluido
Fd = C D A
ρ0 v 2
vt =
2
( ρ − ρ0 ) 2gL
CD
ρ0
Aerodinâmica:
Minimizar CD
Sedimentação
F
Partículas em suspensão num fluido:
Fd = φη R v
P = mg
ρliq
I = V ρliq g = m
ρ
I
P
Velocidade de sedimentação (terminal) (a=0)
F = P−I
ρliq
φ η R vs = mg − m
ρ
vs =
ρliq ⎞
mg ⎛
1
−
φ η R ⎜⎝
ρ ⎟⎠
Ex: Hemoglobina em água a 37ºC
vs ≈ 3.7 cm / 24h
21
Centrifugação
Numa centrifugadora a aceleração da gravidade
é substituida pela aceleração centrípeta
gefect = ω 2 R
R
ω
ω - geralmente em rpm
Valores típicos de rpm: 1000 - 100 000 rpm
Valores típicos de
ρliq ⎞
mgeff ⎛
vs =
1
−
φ η R ⎜⎝
ρ ⎟⎠
gefect
vs =
: 100 g - 50 000 g
mgeff
φη R
= K geff
Centrifugação
22
Centrifugação
Ultra-centrifugação:
Valores típicos de
gefect : 10 000 g - 500 000 g
Muito utilizadas no estudo de formas e dimensões de moléculas
23