Document

UDESC – Universidade do Estado de Santa Catarina
DCC – Departamento de Ciência da Computação
Curso: TADS
Disciplina: Pesquisa Operacional - PES – SI
Notas de Aula
Avaliação: 3 (três) provas ( P1*0,4 + P2*0,3 + P3*0,3 )
Referências bibliográficas:
1.) Taha, H.A. Pesquisa Operacional, 8 edição,
Pearson, 2008;
2.) EHRLICH, Pierre Jacques. Pesquisa operacional:
Curso introdutório. 7. ed. São Paulo: Atlas,
c1991;
3.) SHAMBLIN, James E; STEVENS, G. T. Pesquisa
operacional: uma abordagem básica . São Paulo:
Atlas, 1979
4.) Apostila “Programação Linear” – professor
Maurício Pereira dos Santos. Instituto de
Matemática e Estatística. Universidade do Estado
do Rio de Janeiro. 2000
I.)
INTRODUÇÃO
I.1) O QUE É PESQUISA OPERACIONAL ?
“ METODOLOGIA DE ESTRUTURAR PROCESSOS
APARENTEMENTE NÃO ESTRUTURADOS POR MEIO DA
CONSTRUÇÃO DE MODELOS. UTILIZA UM CONJUNTO DE
TÉCNICAS QUANTITATIVAS COM O INTUITO DE
RESOLVER OS ASPECTOS MATEMÁTICOS”
Pierre Ehrlich-Pesquisa Operacional– Curso Introdutório,
Editora Atlas, 1991
A PO É aplicada à problemas que estão relacionados à
gestão de operações de uma empresa ou organização.
Para isto utiliza um procedimento sistêmico para
solução dos problemas, buscando uma solução que seja
ótima para o problema;
Objetivo do curso: Capacitar o aluno na
formulação e resolução de problemas clássicos de
pesquisa operacional.
I.2) Aplicações da PO:
Programação Matemática
 Linear (mais utilizada)
 Não Linear
 Inteira
Modelos de rede
 Transportes
 Designação
 Grafos
 Teoria das Filas
 Modelos de Simulação
 Modelos de Estoques
 Programação Dinâmica
I.3) Fases de implementação da PO:
a.) Definição do problema. Identificar os três elementos
de um problema de decisão:
. descrição das alternativas de decisão;
. determinação do objetivo do estudo;
. especificação das limitações sob as quais o sistema
modelado funciona.
b.) Construção do modelo. Tentativa de traduzir a
definição do problema em relações matemáticas. Um
modelo é sempre uma aproximação do mundo real.
c.) Validação do modelo. Verifica se o modelo proposto
faz ou não o que diz fazer.
d.) Implementação da solução.
O MODELO GERAL DE PO PODE SER ORGANIZADO NO
SEGUINTE FORMATO:
MAXIMIZAR ou MINIMIZAR FUNÇÃO OBJETIVO
SUJEITO Á RESTRIÇÕES
Exemplo_01: Um fabricante produz dois tipos de ligas ( A
e B) e deseja MAXIMIZAR a receita bruta de sua
empresa. A tabela abaixo ilustra as composições das
ligas, seus preços, limitações na disponibilidade de
matéria-prima.
atividades
itens
Cobre
Zinco
Chumbo
Preço unitário
Venda
Liga_tipo_A
Liga_tipo_B
2
1
1
1
2
3
$30
$50
Matéria-prima
disponivel
16
11
15
a.) IDENTIFICAR QUAIS SÃO AS VARIÁVEIS DE DECISÃO
Seja Xa a quantidade de liga A a ser produzida;
Seja Xb a quantidade de liga B a ser produzida.
b.) IDENTIFICAR A FUNÇÃO OBJETIVO:
MAX Z = 30*Xa + 50*Xb
c.) IDENTIFICAR AS RESTRIÇÕES:
2*Xa + Xb <= 16 (cobre)
Xa + 2*Xb <= 11 ( zinco)
RESTRIÇÕES DE DISPONIBILIDADE DE
RECURSOS
Xa + 3*Xb <= 15 ( chumbo)
Xa >= 0 ; Xb >= 0 ( não pode fabricar quantidades negativas)
Resolução do problema de programação linear:
Analise o gráfico a ser apresentado abaixo:
X2
Chumbo
X1 = 7 ; X2 = 3 ; Z = 310
Ponto Ótimo
Zinco
Regiao
Permissivel
Cobre
X1
As inequações de restrição constituem semi-planos no
espaço, e a intersecção entre elas define o espaço de
solução;
A função objetivo Z que desejamos MAXIMIZAR
constitui uma família de retas paralelas;
Devemos encontrar, no espaço de solução, aquela que
proporciona o valor ótimo da função objetivo
De todas estas retas escolhemos a que maximiza Z e tem
pelo menos um ponto pertencente à região permissível.
Traçando a paralela mais alta possível, que toque pelo
menos um ponto no espaço solução. Este ponto
corresponde à solução ótima desejada.
O ponto ótimo é sempre um dos vértices do espaço
solução.
Substituindo os valores, Xa=7 e Xb=2 obtidos, nas
restrições observamos que todo o cobre e todo o zinco
disponíveis são utilizados !
Entretanto, sobram duas unidades de chumbo não
utilizadas !
Exemplo_02: Resolver graficamente
problema de programação linear
MAX Z = X1 + 2*X2
-X1 + 3*X2 <= 9
X1 – 2*X2 <= 0
2*X1 + X2 <= 10
2*X1 + X2 >= 5
X1 >= 0 ; X2 >= 0.
o
seguinte
Exemplo_03: Resolver graficamente
problema de programação linear
MAX Z = 2*X1 + X2
X1 + 4*X2 <= 24
X1 + 2*X2 <= 14
2*X1 – X2 <= 8
X1 – X2 <= 3
X1 >= 0 ; X2 >= 0.
Resposta : Z = 16.
o
seguinte
Exemplo_04: Uma empresa fabrica produtos 1 e 2. Cada
produto requer um tempo de processamento em cada
um dos três departamentos da empresa. Os lucros de
cada produto são respectivamente $1,00 e $1,50.
Maximizar o lucro, respeitando a capacidade de
produção.
Tempo de processamento:
Departamentos
Produto
A
B
C
1
2
1
4
2
2
2
2
Disponibilidade:
Depto.
Horas
disponíveis
A
160
B
120
C
280
Objetivo: maximizar o lucro
Restrições: horas disponíveis nos departamentos
x1 = quantidade do produto 1 a ser fabricado
x2 = quantidade do produto 2 a ser fabricado
max z = x1 + 1,5x2
S. A .
2x1 +
2x2  160
x1 +
2x2  120
4x1 +
2x2  280
x1, x2  0
2. PROGRAMAÇÃO LINEAR
SISTEMAS DE EQUAÇÔES LINEARES
Dado um sistema de equações lineares:
a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
:
:
:
:
:
:
:
:
an1xn + an2x2 + ... +annxn = bn
através de operações entre as equações podemos
chegar a
x1
= b1
x2
= b2
.
.
.
xn
.
= bn
que equivale ao sistema original,
diretamente a solução. Gauss-Jordan
mas
fornece
O sistema só tem solução única se
No. de equações = No. de incógnitas
Quando temos mais incógnitas, o sistema é subdeterminado. Dado um sistema com m equações e n
incógnitas (n > m), podemos arbitrar n-m variáveis = 0 e
resolver para as restantes.
A forma padrão é:
x1
x2
.
+ a1 m+1xm+1
+...+ a1 nxn
=1
+ a2 m+1xm+1
+...+ a2 nxn
=2
.
.
.
xm + am m+1xm+1
+...+ am nxn = m
|__________________|
|_________________|
Dependentes
independentes
COMO MODELAR MATEMATICAMENTE UM PROBLEMA
DE PROGRAMAÇÃO LINEAR ?
MAX (ou Min) Z = C1X1 + C2X2 + . . . + CnXn
objetivo)
(função
Sujeito à (restrições):
A11*X1 + A12*X2 + ... + A1n*Xn >= ou <= b1
A21*X1 + A22*X2 + ... + A2n*Xn >= ou <= b2
...
Am1*X1 + Am2*X2 + ... + Amn*Xn >= ou <= bn
Onde:
Bi >= 0 para i = 1,...,m
X1 >= 0,..., Xn >= 0
n = atividades que competem, sendo x1,...,xn seus níveis
de atividade
Cj = é o aumento em Z por unidade de atividade j.
m = são os recursos cujos níveis são b1,...,Bm
Aij = é o quanto de recurso i é consumido pela atividade
j.
i = recurso;
j = atividade.
O problema resume-se na Maximização ou Minimização
de uma função linear, a função objetivo, sujeito à
restrições também lineares.
Formulação Equivalente:
max z
=
min –z
n
c x
j1
j
n
j
 (-c )x
j1
j
j
Exemplo_05: Considere a produção de ração animal a
partir de três ingredientes básicos: osso, soja e farinha
de peixe. Os principais nutrientes da ração são: proteína
e cálcio. As necessidades mínimas desses nutrientes por
kilo de ração são 30 % de proteína e 50% de cálcio. Os
custos e quantidades de nutriente (em porcentagem)
por ingrediente são dados na tabela.
Devemos determinar as quantidades de cada
ingrediente a compor a ração de tal forma que as
necessidades mínimas sejam satisfeitas com o menor
custo possível.
Exemplo_06: Problema da dieta balanceada. Sabe-se
que os alimentos, leite, carne e ovos fornecem as
quantidades de vitaminas dadas na tabela abaixo:
Vitaminas Leite(litro) Carne (kg)
A
C
D
Custo
unitário
0,25 mg
25
2,5
2 mg
20
200
$2,2
$17,0
Ovos (dúzia)
Qte. Diária
mínima
10 mg
10
10
$4,2
1 mg
50
10
Deseja-se calcular quais as quantidades de leite, carne e
ovos, a fim de satisfazer as quantidades diárias mínimas
de nutrientes (vitaminas) a um custo mínimo.
Exemplo_07:
Uma fábrica utiliza dois tipos de insumos:
. A a um custo unitário Ca e com uma quantidade
máxima disponível Na;
. B a um custo unitário Cb e com uma quantidade
máxima disponível Nb.
Estes insumos podem ser processados pelos Processos I,
II ou III, a um custo operacional nulo. Serão produzidos
os produtos alpha, beta e gama, que alcançarão preços
de venda P_alpha, P_beta, P_gama respectivamente
(preços unitários).
- Uma unidade de A processada em I produz,
simultaneamente: 5*alpha e 2*gama;
- Uma unidade de A junto com duas unidades de B
conjuntamente
processadas
em
II
produz,
simultaneamente: 3*alpha, 9*beta e 8*gama;
- Uma unidade de B processada em III produz
simultaneamente: 1*alpha, 4*beta, 1*gama.
Formule o problema com programação linear de modo a
minimizar o lucro.
Exemplo_08: Deseja-se formular o problema de modo a
calcular qual a proporção de presuntos, lombinhos e
pernis a serem defumados e qual a proporção a vender
sem defumar. O objetivo é maximizar o lucro, supondo
que toda a produção possa ser vendida.
Podem ser processados (defumados), no máximo,
106 presuntos defumados por dia, sem pagar hora extra.
Também pode-se processar (defumar), no máximo, 315
lombinhos e pernis por dia sem ter que pagar hora
extra.
Disponibilidade de matéria-prima: 480 presuntos,
400 lombinhos e 230 pernis.
Custo de produção para produto acabado (por
unidade)
itens
Defumado
(horário
Normal)
Defumado
(horário extra)
Sem defumar
presunto
5,18
lombinho
4,76
pernil
5,62
6,58
5,54
6,92
0,5
0,48
0,51
A diferença nos preços de venda entre defumado e não
defumado é:
Presunto = 6;
Lombinho = 5;
Pernil = 6.
Adotar a seguinte nomenclatura:
X1 = qte. de presuntos defumados em hora extra;
X2 = qte. de presuntos defumados em hora normal;
X3 = qte. de presuntos vendidos sem defumar;
X4 = qte. de lombinhos defumados em hora extra;
X5 = qte. de lombinhos defumados em hora normal;
X6 = qte. de lombinhos vendidos sem defumar;
X7 = qte. de pernis defumados em hora extra;
X8 = qte. de pernis defumados em hora normal;
X9 = qte. de pernis vendidos sem defumar.
Exemplo_09: Um fazendeiro deseja otimizar as
plantações de arroz e milho na sua fazenda. O seu lucro
por unidade de área plantada de arroz é 5 u.m., e por
unidade de área plantada de milho é 2 u.m. . As áreas
plantadas de arroz e milho não devem ser maiores que 3
e 4 respectivamente. Cada unidade de área plantada de
arroz consome 1 homem-hora, e cada unidade de área
plantada de milho consome 2 homens-hora. A
disponibilidade total de homens-hora é 9.
Objetivo: maximizar o lucro
Restrições: área máxima, mão de obra
x1 = área plantada de arroz
x2 = área plantada de milho
max z = 5x1 + 2x2
x1
S. A .
 3 (área de arroz)
x2  4 (área de milho)
x1 + 2x2  9 (mão de obra)
x1, x2  0
Exemplo_10: Um aluno da disciplina PES, que não quer
ser identificado, quer aproveitar os conhecimentos
adquiridos em programação linear para resolver um
problema particular muito grave. Atualmente ele possui
duas namoradas: Maria e Luisa, das quais gosta com a
mesma intensidade. Ele fez alguns calculos e constatou
que:
– Uma saída de 3 horas com Maria, elegante e
sofisticada, custa $120,00; já com Luisa, mais
simples, o gasto é de $60,00.
– Cada saída com Maria consome 3000 calorias;
com Luisa, mais extrovertida e alegre, o gasto
de energia é o dobro.
– Seus afazeres (trabalho, estudos) consomem
muito do seu tempo e energia, de modo que,
mensalmente lhe sobram 30 horas e 40000
calorias para as atividades sociais. Depois de
pagar as contas da república onde mora,
sobram $360,00 para diversão.
– O objetivo desse aluno é planejar sua vida
social, de modo a obter o número máximo de
saídas. Formular e resolver o problema
graficamente.
Objetivo: maximizar número de saídas
Restrições: dinheiro, tempo e calorias
x1 = saídas com Maria
x2 = saidas com Luisa
max z = x1 + x2
120x1 +
S.A.
3x1 +
60 x2  360
3x2
 30
3000x1 + 6000x2  40000
x1 , x 2  0
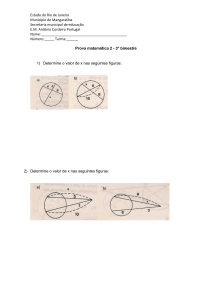
Exemplo_11: Apresentar o gráfico do problema:
max z = 4x1 + 2x2
2x1 + x2  12
S. A .
 8
x1
x2  4
x1, x2
0
Geometria e álgebra em programação linear
Conjuntos convexos: um conjunto é convexo se, unindo
dois pontos do conjunto por um segmento de reta, todos
os pontos deste segmento também pertencerão ao
conjunto.
Inserir figuras ilustrativas
Semi-espaços: uma solução considerando a equação
abaixo
a1*x1 + a2*x2 + ... + na*xn = b
divide o espaço R de dimensão n em 3 subconjuntos:
. = dá um hiperplano, com uma reta em RxR, e um plano
em RxRxR
. > dá um semi-espaço aberto;
. < dá um semi-espaço aberto;
Por exemplo, dado a reta 2x + 4y = 8 , divide o espaço
como mostrado na figura abaixo:
y
>
<
x
=
. Poliedrico convexo: é dado pela intersecção de um
número finito de semi-espaço fechado em R**m.
. Conjunto poligonais convexos podem ser: limitado e
não-limitado
limitado
Não- limitado
O conjunto convexo das soluções aceitáveis é chamado
de conjunto factível ou conjunto viável.
Semi-espaços são conjuntos convexos, e a intersecção de
um número finito de semi-espaços fechados em Rn é um
conjunto poliédrico convexo
Exemplo_12: Maximizar Z = 2x + 5y
Sujeito à:
X+2y <= 4
X – y <= 4
X >= 1
Y >= -1
y
x=1
x
y = -1
Seja f uma função linear definida num conjunto poliédrico
fechado convexo S. A função S assume seu máximo ou
seu mínimo num ponto extremo de S. Portanto, para
resolver um problema de programação linear basta
encontrar os pontos extremos e selecionar aquele que
maximiza (ou minimiza) a função objetiva.
Para resolver um problema de P.L., basta encontrarmos
os pontos extremos e avaliar a função objetivo em cada
um.
Para que um problema de P.L. possa ser resolvido
algebricamente, as inequações devem ser transformadas
em igualdades.
Adicionamos variáveis de folga, também não negativas:
Max
z = c1x1 +c2x2 +c3x3
a11x1 + a12x2 + a13x3 ≤ b1
 a11x1 + a12x2 + a13x3 + x4 = b1
S. A . a21x1 + a22x2 + a23x3 ≥ b2  a21x1 + a22x2 + a23x3 + x5 = b2
a31x1 + a32x2 +a33x3 = b3
 a31x1 + a32x2 + a33x3 = b3
Dado um conjunto de m equações linearmente
independentes e n incógnitas, onde n > m, se define
como solução básica a solução para o conjunto de
equações em que ( n – m) variáveis são feitas iguais a 0 e
as restantes são obtidas da resolução do sistema de
equações.
Exemplo_13: Seja o sistema abaixo:
X1 + X2 + 3*X3 – X4 + X5 = 6
X1 + 2*X2 + 2*X3 – X4 + 2*X5 = 2
Temos m = 2 e n = 5
Cada solução básica terá (5 - 2) = 3 variáveis iguais a 0,
por exemplo X3, X4 e X5 e ( 5 - 3) = 2 obtidas da resolução
do sistema.
Ou seja, X1 = 10 e X2 = -4. É óbvio que variando-se as
variáveis feitas iguais a zero teremos novas soluções
básicas.
O número de soluções básicas que podem ser obtidas é
dado por:
(
)
As variáveis diferentes de zero são chamadas de variáveis
básicas e as iguais a zero são chamadas de variáveis não
básicas.
As variáveis de folga são acrescentadas as inequações
para transformá-las em equações.
Exemplo_14: Dado o seguinte problema de PL
(MAX) Z = 20*X1 + 60X2
S.A.
70*X1 + 70*X2 <= 4900
90*X1 + 50*X2 <= 4500
2*X1 <= 80
3*X2 <= 180
X1,X2 >= 0
Acrescentando as variáveis de folga às quatro restrições
do modelo:
(1)
(2)
(3)
(4)
70*X1 + 70*X2 + F1 = 4900
90*X1 + 50*X2 +F2 = 4500
2*X1 +F3 = 80
3*X2 + F4 = 180
Tem-se então um sistema de equações lineares com 4 (m)
equações e 6 (n) variáveis. Então tem-se:
( )
= 15 soluções básicas
Observação: Embora as variáveis de folga sejam usadas
para transformar inequações em equações, elas possuem
um significado físico relacionado ao problema que está
sendo modelado.
Cada solução básica do exemplo 13 será obtida
escolhendo-se 2 variáveis e fazendo-as iguais à zero, e
resolvendo–se o sistema para as 4 variáveis restantes.
Vide a tabela a seguir:
número
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
não básicas
Báscias
condição
x1=0 , x2=0 F1=4900 , F2=4500 , F3 = 80 , F4 = 180 praticável
x1=0, F1=0 X2=70 , F2 = 1000 , F3 = 80 , F4 = -30 impraticável
x1=0, F2=0 X2=90, F3 = 80 , F4 = -90 , F1 = -1400 impraticável
x1=0, F3=0
O = 80
impossível
x1=0, F4=0
F3=80, x2=60 , f1 = 700 , f2 = 1500
praticável
x2=0, F1=0 F3 =-60, F2 = -1800 , F4 = 180 , X1 =70 impraticável
x2=0, F2=0 F3 = -20 , F1 = 1400 , X1 = 50 , F4 = 180 impraticável
x2=0, F3=0 F1= 2100, F2 = 900 , X1 = 40, F4=180
praticável
x2=0, F4=0
O =180
impossível
F1=0, F2=0
X1 = 25 , X2 = 45 , F3 = 30 , F4 = 45
praticável
F1=0, F3=0 X1 = 40 , X2 = 30 , F2 = -600 , F4 = 90 impraticável
F1=0, F4=0 X1 = 10 , X2 = 60 , F3 = 60 , F2 = 600
praticável
F2=0, F3=0 X1 = 40, X2 = 18, F1 = 840 , F4 = 126
praticável
F2=0, F4=0X1 = 16,7 , X2 = 60 , F3 = 46,7 , F1 = -466,6impraticável
F3=0, F4=0 X1 = 40 , X2 = 60 , F1 = -2100 , F2 =2100 impraticável
Z
0
3600
800
3200
3800
1880
X2
4
R3
3
2
14
5
R4
15
12
10
11
9
13
6
1
8
7
X1
R2
R1
No gráfico podemos observar que a solução ótima só
pode ser um dos vértices (pontos extremos) do espaço
solução, pois, eles são justamente as soluções básicas
praticáveis. Isto vem do fato de que o espaço solução é
sempre um conjunto convexo onde cada solução básica
corresponde a intersecção de tantas restrições quantas
forem as variáveis de decisão do modelo ( duas, x1 e x2,
neste exemplo).
Observação: Se um modelo de PL possui uma única
solução ótima, então ela é uma solução básica do sistema
de equações lineares formado pelas restrições do modelo
acrescidas das suas respectivas variáveis de folga.
Observação: No caso de termos mais de uma solução
ótima, teremos sempre um número infinito de soluções
ótimas, pois, serão ótimos todos os pontos que unem
dois vértices (pontos extremos) adjacentes, ou seja, todos
os pontos de um dos lados do espaço solução.
Observação: O exemplo apresentado indica que esta
maneira de resolver o problema de PL torna-se
impraticável, quando por exemplo, temos um problema
com 50 restrições e 100 variáveis. Neste caso teríamos
10**29 possíveis soluções básicas !!!
Método Simplex
O método simplex de PL usa os conceitos básicos de
álgebra matricial para achar a intersecção de duas ou
mais linhas ou planos. O Simplex é uma maneira
sistemática de pesquisar os vértices de um poliedro
convexo, de modo a em um número finito de iterações
fornecer a solução, ou indicar que esta não existe.
Começa com alguma solução viável que satisfaz todas as
restrições e sucessivamente obtêm soluções nas
intersecções que oferecem valores melhores para a
função objetivo.
O método simplex examina apenas um número pequeno
destas soluções básicas para encontrar a solução básica.
Duas soluções básicas praticáveis são adjacentes se elas
diferem por apenas uma variável não básica. Como o
total de variáveis é a soma das não básicas com as
básicas, elas diferem também por uma variável básica.
Considerando o exemplo anterior, então temos que as
seguintes soluções básicas são adjacentes:
Número 01:
VB
VNB
F1 = 4900
X1 = 0
F2 = 4500
X2 = 0
F3 = 80
F4 = 180
Número 08:
VB
VNB
F1 = 2100
F3 = 0
F2 = 900
X2 = 0
X1 = 40
F4 = 180
O número de soluções básicas praticáveis adjacentes à
cada solução básica é igual ao número de variáveis de
decisão do modelo ( duas, x1 e x2 no caso deste
exemplo). Assim, pode ser visto no gráfico onde são
mostradas as soluções básicas, a solução 1 tem duas
adjacentes: a 5 e a 8.
O método Simplex considera que: se uma solução básica
é melhor que as suas adjacentes, então ela é a solução
ótima.
Aplicação do método Simplex:
• colocar na forma padrão, adicionando as
variáveis de folga
• montar o quadro do SIMPLEX, conforme o
seguinte esquema:
• I: matriz identidade
x (atividades)
x (folga)
A
I
b
-c
0
0
i.)
ii.)
iii.)
Selecionar a coluna com o valor de C mais
negativo;
Encontre para todas as linhas i, a menor
relação Bj/Aij , com Aij > 0. O valor escolhido
será o pivô.
Proceder com a operação-pivô que tal maneira
a tornar o coeficiente Xij igual a 1 e todos os
outros coeficientes da coluna j nulos.
Identificar um novo ponto extremo.
iv.)
Repita as etapas i, ii e iii até que não haja mais
valores negativos na última linha c.
Exemplo_16:
Max z = 30 x1 + 50 x2
2 x1 + x2  16
x1 + 2x2  11
x1 + 3x2  15
x1 , x 2  0
forma padrão :
2 x1 + x2 + x3
x1 + 2x2
+ x4
x1 + 3x2
+ x5
= 16
= 11
= 15
x1
x2
x3
x4
x5
2
1
1
0
0
16
1
2
0
1
0
11
1
3
0
0
1
15
0
0
0
0
-30
-50
A tabela inicial (acima) apresenta como base inicial, por
ser mais simples, as variáveis de folga. Se analisarmos o
gráfico a seguir corresponde a tomar-se a origem como
solução básica inicial.
Porém, para otimizar a solução acima é necessário aplicar
o método simplex ( fases de i a iv), em que serão
identificados os outros pontos extremos do poliedro
convexo, e garantindo assim que estaremos passando de
um ponto extremo a outro.
X1
2
1
1
-30
X2
1
2
3
-50
X3
1
0
0
0
X4
0
1
0
0
X5
0
0
1
0
b
Z
16
11
15
0
0
0
0
1
Esta posição representa o primeiro máximo a ser
atingido.
Divide L3 por 3:
X1
2
1
1/3
-30
X2
1
2
1
-50
X3
1
0
0
0
X4
0
1
0
0
X5
0
0
1/3
0
Multiplica L3 por (-2) e soma com L2:
b
16
11
15
0
Z
0
0
0
1
X1
2
1/3
1/3
-30
X2
1
0
1
-50
X3
1
0
0
0
X4
0
1
0
0
X5
0
- 2/3
1/3
0
b
16
1
5
0
Z
0
0
0
1
Multiplica L3 por (-1) e soma com L1:
X1
1 2/3
1/3
1/3
-30
X2
0
0
1
-50
X3
1
0
0
0
X4
0
1
0
0
X5
- 1/3
- 2/3
1/3
0
b
11
1
5
0
Z
0
0
0
1
Multiplica L3 por 50 e soma com L4:
X1
1 2/3
1/3
1/3
-13 1/3
X2
0
0
1
0
X3
1
0
0
0
X4
0
1
0
0
X5
b
- 1/3 11
- 2/3
1
1/3
5
16 2/3 0
Z
0
0
0
250
Realizadas as operações Pivô na coluna 2, continua-se o
processo selecionando agora a coluna 1, linha 2.
X1
1 2/3
1/3
1/3
-13 1/3
X2
0
0
1
0
X3
1
0
0
0
X4
0
1
0
0
X5
- 1/3
- 2/3
1/3
16 2/3
Multiplicou-se a segunda linha por 3.
b
11
1
5
0
Z
0
0
0
250
Multiplicou-se a segunda linha por -1/3 e somou-se á
terceira linha.
Multiplicou-se a segunda linha por -5/3 e somou-se à
primeira.
Multiplicou-se a segunda por 40/3 e somou-se a quarta
linha.
Realizadas as operações Pivo na coluna 1, continua-se o
processo selecionando agora a coluna 5, linha 1.
X1
0
1
0
0
X2
0
0
1
0
X1
0
1
0
0
1
0
0
0
X2
0
0
1
0
X3
X4
-5
3
-1
40
X3
X4
1/3
-1 2/3
2/3
- 1/3
- 1/3
2/3
3 1/3 23 1/3
X5
3
-2
1
-10
b
6
3
4
0
X5
1
0
0
0
Z
0
0
0
290
b
2
7
2
Solução ótima é dada por:
X1 = 7; X2 = 2 ; X3 = 0 ; X4 = 0 ; X5 = 2 ; Z = 310.
Z
0
0
0
310
As variáveis X3 e X4 são não básicas.
X2
X1 = 7 ; X2 = 3 ; Z = 310
Ponto Ótimo
X1
– Algoritmo do Simplex:
– Escolha do pivô:
• na última linha (linha z), escolha o
coeficiente mais negativo (escolha da
coluna)
• para a coluna selecionada, escolher a
menor relação bj / aij (para aij >0) (escolha
da linha)
– Escolhido o pivô, fazemos as operações de linha
para que este seja 1 e os outros elementos da
coluna sejam 0.
– Os passos são repetidos até que não existam
elementos negativos na última linha (linha z), o
que significa que a função objetivo não pode
ser melhorada.
Exercícios SIMPLEX
1 Max z = 5x1 + 2x2
x1
 3
S. A . x2  4
x1 + 2x2  9
x1, x2  0
2 Max z= 3x1 + 2x2 + 6x3
6x1 + 3x2 - 4x3  60
2x1 - 4x2 + 4x3  40
S.A
3x1 + 3x2 + 3x3  60
x1 , x 2 , x 3  0
3 Max z = 4x1 + 2x2
2x1 + x2
S. A .
x1
 12
 8
x2  4
x1, x2  0
4 Min z = - x1 + 2x2
-x1 + x2
 1
S.A 6x1 + 4x2  24
x2  2
x1,x2  0
5 Max z = 2x1 + x2
x1 + x 2
 5
S.A x1 + 2x2  8
X1  4
x1,x2  0
Resposta: X1 = 4 ; X2 = 1 ; Z = 9)
6 Max z = 7x1 + 3X2 + 2X3
5x1 + 2x2 + 2X3
 19
S.A 2x1 + x2 + 2X3  8
x1,x2, x3,  0
Resposta: Z = 27
Solução 1
x1
x2
x3
x4
x5
b
1
0
1
0
0
3
0
1
0
1
0
4
1
2
0
0
1
9
-5
-2
0
0
0
0
1
0
1
0
0
3
0
1
0
1
0
4
0
2
-1
0
1
6
x2 = 3 (área de milho)
0
-2
5
0
0
15
x3 = 0 (folga área de arroz)
1
0
1
0
0
3
0
0
1/2
1
-1/2
1
0
1
-1/2
0
1/2
3
0
0
4
0
1
21
Resposta:
x1 = 3 (área de arroz)
x4 = 1 (folga área de milho)
x5 = 0 (folga mão de obra)
z = 21 (lucro)
Resposta:
Solução 2
x1 = 0
fab prod 1
x1
x2
x3
x4
x5
x6
b
x2 = 5
fab prod 2
6
3
-4
1
0
0
60
x3 = 15
fab prod 3
2
-4
4
0
1
0
40
3
3
3
0
0
1
60
-3
-2
-6
0
0
0
0
8
-1
0
1
1
0
100
½
-1
1
0
1/4
0
10
3/2
6
0
0
-3/4
1
30
0
-8
0
0
3/2
0
60
x4 = 105 sobra rec 1
x5 = 0
sobra rec 2
x6 = 0
sobra rec 3
z=100
lucro total
33/4
0
0
1
7/8
1/6
105
¾
0
1
0
1/8
1/6
15
¼
1
0
0
-1/8
1/6
5
2
0
0
0
1/2
4/3
100
Solução 3
x1
x2
x3
x4
x5
b
2
1
1
0
0
12
1
0
0
1
0
8
0
1
0
0
1
4
-4
-2
0
0
0
0
I
II
III
1
1/2
1/2
0
0
6
0
-1/2
-1/2
1
0
2
0
1
0
0
1
4
0
0
2
0
0
24
Resposta1:
Múltiplas
soluções
x1 = 6
x2 = 0
Fazendo mais uma iteração :
x3 = 0
x4 = 2
1
1/2
1/2
0
0
6
x5 = 4
0
-1/2
-1/2
1
0
2
z = 24
0
1
0
0
1
4
0
0
2
0
0
24
1
0
1/2
0
-1/2
4
0
0
-1/2
1
1/2
4
0
1
0
0
1
4
0
0
2
0
0
24
X1
X2
X3
X4
X5
b
X1
X2
X3
X4
X5
B
-1
1
1
0
0
1
0
5/3
1
1/6
0
5
6
4
0
1
0
24
1
2/3
0
1/6
0
4
0
1
0
0
1
2
0
1
0
0
1
2
-1
2
0
0
0
0
0
8/3
0
1/6
0
4
X1= 4
X2=0
X3=5
X4=0
X5=2
Z = -4
Outras formas de restrição
As restrições podem ser também na forma:
>= ou =.
A restrição >= tem dois efeitos principais:
. reduz o tamanho do campo viável ou aceitável;
. requer uma modificação do método básico de solução.
A restrição do tipo >= (por exemplo, X2 >= 10) exclui o
ponto (0,0). Assim a solução inicial antes utilizada, isto é,
quando todas as variáveis decisórias eram zero, não é
viável.
Como o algorítmo Simplex procede de uma solução viável
para uma situação melhorada, deve-se obter um novo
ponto de partida.
Existem vários métodos para tratar este problema. Um
deles utiliza-se de uma variável artificial. Convertendo
uma desigualdade em uma igualdade, a variável de folga
deve ser acrescentada do outro lado da desigualdade.
Exemplo_16:
x1
x2
x3
x4
1
1
1
0
10
1
2
0
-1
8
-1
1
0
0
2
-2
-2
0
0
0
Com ser pode ser verificado, não identifica-se a matriz
identidade. Este problema é resolvido acrescentando
uma outra variável denominada de variáveis artificiais (y1
e y2).
Então, a solução do problema inicia-se com a introdução
de variáveis artificiais, de modo a obter-se uma forma
padrão, ou seja, um ponto extremo, mas não um ponto
extremo do problema inicial.
x1 + x2 + x3
x1 +2x2
= 10
- x4 + y1
-x1 + x2
= 8
+ y2 = 2
Dado que a variável artificial foi acrescida o quadro
simplex é construído:
x1
x2
x3
x4
y1
y2
1
1
1
0
0
0
10
1
2
0
-1
1
0
8
-1
1
0
0
0
1
2
-2
-2
0
0
0
0
0
As variáveis artificiais não fazem parte do problema,
portanto não podem fazer parte da solução. Como
“elimina-las” encontrando uma solução inicial válida?
Para estes tipos de restrição, deve-se empregar o
SIMPLEX em duas fases.
Assim:
Fase I: encontrar uma solução factível inicial,
minimizando a soma das variáveis artificiais sobre um
novo conjunto.
Fase II : Otimizar função objetivo z
Fase I:
a. Em cada expressão (restrição) <= ou >= introduzir as
variáveis de folga. Em seguida, em cada expressão que
era = ou >= , adicionar uma variável artificial.
b. Monte a tabela
c. Adicione no final da tabela mais uma linha (W) de
coeficientes Dij debaixo da última linha, onde:
Dij = -( A1j + A2j + . . . + Amj) e inserir zeros nas colunas
correspondentes às variáveis artificiais. Adicione debaixo
de B, na última linha:
Bw = - ( B1 + B2 + . . . + Bm).
No cálculo do valor de Dj e Bw só se consideram os
elementos Aij e Bj das linhas que incluem variáveis
artificiais.
d. Aplicar o algoritmo do Simplex utilizando a última linha
como sendo a de decisão para a inclusão de variáveis de
base.
e.) Quando a última linha tiver chegado ao valor ótimo,
verifique W. Se W = 0, quer dizer que a soma das
variáveis artificiais é 0 (zero) e , portanto, obtivemos um
ponto extremo do problema original.
Desprezar todas as variáveis não básicas Xj, cujos
elementos da última linha sejam > 0, variáveis artificiais,
de modo que elas nunca possam ser diferentes de zero.
Abandone a última linha. Agora, aplique o Simplex
empregando a nova última linha.
Se W é diferente de zero, isto quer dizer que o problema
inicial tem um conjunto de restrições inconsistentes e não
há solução factível para o problema original !
forma padrão:
x1 + x2 + x3
x1 + 2x2
-x1 + x2
= 10
- x4 + y1
= 8
+ y2 = 2
x1
x2 x3 x4 y1 y 2
1
1
1
0
0
0
10
1
2
0
-1 1
0
8
-1
1
0
0
0
1
2
-2
-2
0
0
0
0
0
0
-3
0
1
0
0
z
-10 w
Resolvendo usando a linha w como linha de decisão.
Exemplo_17
Dado a função objetivo:
Max Z = -X1 -6X2 +7X3 – X4 – 5X5
S.A.
5X1 – 4X2 + 13X3 – 2X4 + X5 >= 20
X1 – X2 + X3 – X4 + X5 = 8
2X1 + X2 - X3 + 4X4 <= 15
X1,..., X5 >= 0
Neste exemplo, introduz-se as variáveis artificiais Y1
e Y2 além das de folga X6 e X7.
A função objetivo do problema artificial é dada por:
Min Y1 + Y2 = Max w = - Y1 – Y2, ou seja:
W + y1 + Y2 = 0
Sujeito à:
5X1 ... + X5 – X6
+ Y1
X1 ... +X5
= 20
+ Y2 = 8
2X1 + ...
+ X7
X1,..., X7 >= 0 , Y1 >= 0 , Y2 >= 0
Z
W
5X1 - 4X2 + 13X3
X1 - X2 + X3
2X1 + X2 - X3
1
6
-7
-6 5
-14
- 2X4 + X5 - X6
- X4 + X5
+ 4X4
1
5
0
3
-2
1
Y1
Y2
+X7
0 0
0 0
0
0
20
8
15
0
-28
Exemplo_18
Maximizar a função objetivo sujeito as seguintes
restrições:
Max Z = 2X1 + X2 + X3
S.A.
3X1 + 4X2 + X3
=5
X1 + X2 + 2X3 = 3
X1 >= 0 ; X2 >= 0 ; X3 >= 0
L1
L2
L3
L4
X1
3
1
-2
-4
L1
L2
L3
L4
X1
3/4
1/4
-1 1/4
- 1/4
L1
L2
L3
L4
X1
5/7
1/7
-1 1/7
0
X2
4
1
-1
-5
X3
1
2
-1
-3
Y1
1
0
0
0
X2
1
0
0
0
X3
1/4
1 3/4
- 3/4
-1 3/4
Y1
1/4
- 1/4
1/4
1 1/4
X2
1
0
0
0
X3
0
1
0
0
Y1
2/7
- 1/7
1/7
1
Y2
0
1
0
0
b
5
3
0
-8
Y2
0
1
0
0
Y2
- 1/7
4/7
3/7
1
b
1 1/4
1 3/4
1 1/4
-1 3/4
L4/4
Z
W
L1 / 4
L1 - L2
Z L1 + L3
W 5L1 + L4
b
1
1
2
0
(-1/4)L2 + L1
L2/(7/4)
Z (3/4)L2 + L3
W (7/4)L2 + L4
Com W = 0 chega-se ao final da fase I, e dá-se início a fase
II, abaixo apresentada.
L1
L2
L3
X1
5/7
1/7
-1 1/7
X2
1
0
0
X3
0
1
0
1
1
2
L1
L2
L3
X1
1
0
0
X2
1 2/5
- 1/5
1 3/5
X3
0
1
0
b
1 2/5
4/5
3 3/5
b
Ao obter-se W = - y1 - y2 igual à zero no terceiro tableau,
chegou-se ao ponto X2 = 1 ; X3 = 1 ; X1 = 0, como base
inicial para o problema original. Neste ponto Z já tem um
valor não nulo.
No quarto tableaux abandona-se o problema artificial e
concentra-se em otimizar o problema original.
Soluções múltiplas:
Se uma variável não-básica tem coeficiente de custo
igual à zero numa solução ótima, isto quer dizer que ela
pode ser introduzida na base sem alterar o valor da
função objetiva.
Portanto, também é uma base ótima (ponto
extremo) e qualquer combinação linear destes dois
pontos também é ótima.
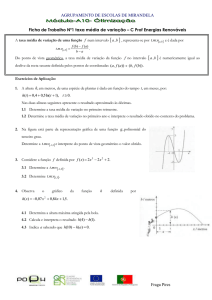
Exemplo_19
Encontra-se a solução do problema graficamente e pelo
método Simplex e análise ambas as soluções.
Max Z = 4X1 + 2X2
SA:
2X1 + X2 <= 12
X1 <= 8
X2 <= 4
X1, X2 >= 0
Conclusão:
Geometricamente, isto pode ser visualizado dizendose que o hiperplano definido pela função objetiva ( reta
no plano, no caso de duas variáveis) encosta numa das
arestas do conjunto convexo que define o espaço das
soluções factíveis (viáveis). Portanto, neste caso, qualquer
combinação linear originando um ponto entre dois
extremos obtidos neste exemplo resulta no mesmo valor
de Z máximo.
Sem Soluções:
Se w é diferente de zero significa que o problema possui
uma série de restrições inconsistentes, e não solução
factível para o problema.
Exemplo_20
Encontra-se a solução do problema graficamente e pelo
método Simplex e análise ambas as soluções.
Max Z = 2X1 + X2
SA
X1 –X2 <= 0
X2 <= 2
X1 + 2X2 >= 8
X1, X2 >= 0
Soluções ilimitadas:
Todos os possíveis coeficientes (pivôs) são negativos
na sua coluna equivalente, ou seja, não há limitante. Isto
leva a solução para valor infinito, sem tornar as outras
varáveis básicas negativas.
Exemplo_21
Encontra-se a solução do problema graficamente e pelo
método Simplex e análise ambas as soluções
Max Z = 2X1 + 3X2
SA
-4X1 + 2X2 <= 8
-4X1 + 4X2 >= 4
X1 + X2 >= 5
X1, X2 >= 0
Soluções degeneradas:
Ocorre quando uma variável básica assume valor zero.
Exemplo_22
Encontra-se a solução do problema graficamente e pelo
método Simplex e análise ambas as soluções.
Max Z = 3X1 + 9X2
SA
X1 + 4X2 <= 8
X1 + 2X2 <= 4
X1, X2 >= 0
Programação Linear Inteira (PLI)
PLIs são programações lineares nas quais algumas ou
todas as variáveis estão restritas à valores inteiros
ou discretos. Os algorítimos de PLI são baseados na
exploração da PL e envolve três etapas (Taha, 2008):
a.) Relaxe a região de soluções da PLI, eliminando a
restrição inteira imposta a todas as variáveis
inteiras e substituindo qualquer variável y por
uma faixa contínua. O resultado da relaxação é
um PL normal;
b.) Resolva a PL e identifique a solução ótima
contínua;
c.) Começando do ponto ótimo contínuo, adicione
restrições
especiais
que
modifiquem
iterativamente a região de soluções da PL, de
maneira que, a certa altura, resultará em um
ponto extremo ótimo que satisfaz os requisitos
inteiros.
Branch and Bound: algorítmo de programação
inteira
Exemplo_23
Maximizar Z = 5X1 + 4X2
SA:
X1 + X2 <= 5;
10X1 + 6X2 <= 45;
X1, X2 inteiros, não negativos
Os pontos de grade da figura abaixo definem a
região de soluções da PLI.
De acordo com o gráfico, a solução ótima da
programação linear (PL) é definida com base na
eliminação das restrições inteiras. A solução ótima é
dada por:
X1 = 3,75 ; X2 = 1,25 ; Z = 23,75.
Os pontos de grade da figura acima definem as
regiões de soluções da PLI.
Como a solução ótima da PL não satisfaz os
requisitos inteiros, o algoritmo B&B modifica a
região de soluções, de maneira a identificar a
solução ótima para a programação linear inteira
(PLI).
Em primeiro lugar, seleciona-se uma das variáveis
inteiras cujo valor ótimo na PL seja não inteiro (X1);
Selecionando X1, a região 3 < X1 < 4 da região de
soluções de PL não contêm nenhum valor inteiro de
X1 e , por isso, pode ser eliminada como não
promissora.
Isto equivale a substituir a PL original por duas novas
PLs:
. Região da PL2 ( X1 <= 3)
. Região da PL3 ( X1 >= 4)
Os dois espaços combinados de PL2 e de PL3 contêm
a mesma quantidade de pontos inteiros viáveis da
PLI original, ou seja: PLI= PL2+PL3
Como as novas restrições são mutuamente
exclusivas, então PL2 e PL3 serão tratadas como PLs
separadas. Ou seja, a solução ótima se encontra em
PL3 ou em PL4.
Portanto, estaremos resolvendo o problema de
programação linear inteira (PLI), lidando com uma
sequencia de PLs (ramificação).
Vamos primeiro, começar analisando PL2.
Maximizar Z = 5X1 + 4X2
SA:
X1 + X2 <= 5
10X1 + 6X2 <= 45
X1 <= 3
X1,X2 >= 0
A solução de PL2 é dada por:
X1 = 3 ; X2 = 2 e Z = 23
Esta solução satisfaz os requisitos inteiros para
X1 e X2. Não precisa ser mais investigada !
Vamos analisar PL3. Como o Z ótimo = 23,75 na
PL, e por acaso todos os coeficientes da função
objetivo são inteiros, é impossível que a PL3 (
que é mais restritiva que a PL1) produza uma
solução inteira melhor do que Z > 23. Portanto,
PL3 é descartado !
Assim X1 = 3; X2 = 2 e Z = 23 é a solução ótima.
A figura acima demonstra que poderíamos
também ter iniciado o algoritmo de B&B por
PL3, o que pode acontecer na prática.
Pelo fato de termos iniciado o problema
analisando PL3, gerou-se um número maior de
subproblemas como pode ser constatado na
figura acima.
Resumo do algoritmo B&B (Taha, 2008):
Etapa_1: Selecione uma PLi, o próximo subproblema
a ser analisado. Resolva a PLi e tente interpretá-la
usando uma das três condições:
a. O valor ótimo de Z da PLi n ão pode dar um
valor objetivo melhor do que o limite inferior atual
b. A PLi dá uma solução inteira viável melhor do
que o limite inferior atual;
c. A PLi não tem nenhuma solução viável.
Na etapa_1 podem surgir dois casos:
. Se a PLi for interpretada e uma solução melhor
for encontrada, atualize o limite inferior. Se todos os
subproblemas tiverem sido descartados, pare; a PLI
ótima está associada com o limite finito atual. Se não
existir nenhum limite inferior finito, o problema não
tem solução viável. Senão, determine i = i +1 e repita
a etapa_1
. Se a PLi não for interpretada, vá para a
etapa_2 para ramificar.
Etapa_2: (Ramificação). Selecione uma das variáveis
inteiras Xi, cujo valor ótimo Xi na solução da PLi não
seja inteiro.
As etapas dadas se aplicam a problemas de
maximização. Para minimização, substituímos o
limite inferior por um limite superior.
Exercício
Desenvolva a árvore B&B para cada um dos
seguintes problemas. Por conveniência, sempre
selecione X1 como a variável de ramificação no nó 0.
Max Z = 3X1 + 2X2
SA
2X1 + 5X2 <= 9
4X1 + 2X2 <= 9
X1 , X2 >= 0 e inteiras
Capítulo 5 – Otimização em redes
Os problemas de otimização em redes apresentados
neste capítulo tratam de aplicações tradicionais, tais
como: encontrar o caminho mais curto entre dois
pontos, determinar o fluxo máximo em uma rede de
tal maneira a satisfazer os requisitos de suprimentos
e demanda em diferentes locais.
A solução destes problemas pode ser obtida por
meio de uma variedade de algoritmos de otimização
em redes. Neste capítulo veremos dois algoritmos:
. Resolução do problema de caminho mínimo
(Dijkstra)
. Resolução do problema para fluxo máximo
Definições: Uma rede consiste em um conjunto de
nós conectados por arcos. A notação para descrever
uma rede é dada por (N,A), na qual N representa o
conjunto de nós e A representa o conjunto de arcos.
Como exemplo, a rede da figura abaixo é
representada por:
N = [ 1,2,3,4,5]
A = [(1,2), (1,3), (2,3), (2,5), (3,4), (3,5), (4,2), (4,5) ]
Associado com cada rede está um fluxo. Em geral, o
fluxo em uma rede é limitado pela capacidade de
seus arcos, que pode ser finita ou infinita.
Diz-se que um arco é orientado ou dirigido se ele
permitir fluxo positivo em uma direção e fluxo zero
na direção oposta. Uma rede orientada é aquela em
que todos os arcos são orientados.
Um caminho representa uma sequência de arcos
distintos que ligam dois nós passando por outros
nós, independentemente da direção de fluxo em
cada arco.
Uma rede conectada é uma rede tal que todos os
pares de nós estão ligados por no mínimo um
caminho.
Uma árvore é uma rede conectada sem ciclos
formada por um subconjunto de todos os nós, e uma
árvore geradora corresponde a uma árvore que liga
todos os nós de rede. Veja a figura acima.
5.1 Caminho Mínimo
O problema do caminho mínimo determina o
caminho mais curto entre um destino e uma origem
em uma rede
Algorítmo de Dijkstra: determina o caminho mais
curto entre o nó de origem e qualquer outro nó da
rede.
Fases do algoritmo:
Fase_0: Dado uma rede, rotule o nó de origem (nó 1)
com o rótulo permanente [0,--]. Determine i = 1;
Os rótulos dos nós do algoritmo de Dijsktra são de
dois tipos: temporários e permanentes. Um rótulo
temporário é modificado se for possível encontrar
uma rota mais curta até um nó. Se não for possível
encontrar nenhuma rota melhor, o status do rótulo
temporário muda para permanente.
Fase_1: Calcular os rótulos temporários [Ui + Dij, i]
para cada nó j que puder ser alcançado partindo do
nó i, contando que j não seja permanentemente
rotulado.
a.) Se o nó j já estiver rotulado com [Uj,k]
passando por um outro nó k, e se Ui + Dij <
Uj, substitua [Uj, k] por [ ui + Dij, i];
b.) Se todos os nós tiverem rótulos
permanentes, pare. Caso contrário,
selecione o rótulo [ Ui, S], cuja distância
(=Uj) é a mais curta entre todos os rótulos
temporários (empates são resolvidos
arbitrariamente). Determine i = r e repita a
etapa i;
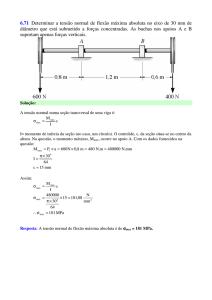
Exemplo: A rede da figura abaixo fornece as rotas
possíveis e seus cumprimentos em milhas entre a cidade
1 ( nó 1) e quatro outas cidades (nó 2 a 5). Determine os
caminhos mais curtos entre a Cidade 1 e cada uma das
quatro outras cidades.
Iteração 0: Designe o rótulo permanente [0, --] ao nó 1;
Iteração 1: Os nós 2 e 3 podem ser alcançados com base
no nó 1 ( último no rotulado permanente).
Assim, a lista de nós rotulados (permanentes e
temporários ) fica como demonstrado na tabela abaixo:
Para os dois rótulos temporários [100,1] e [30,1], o nó 3
resulta na menor distância (U3 = 30). Assim, o status do
nó 3 muda para permanente.
Iteração 2. Os nós 4 e 5 podem ser alcançados com base
no nó 3, e a lista de nós fica como demonstrado na tabela
abaixo:
O status do rótulo temporário [40,3] no nó 4 muda para
permanente (U4 = 40).
Iteração 3. Os Nós 2 e 5 podem ser alcançados com base
no nó 4. Assim, a lista de nós rotulados é atualizada
conforme demonstrado na tabela abaixo:
O rótulo temporário do nó 2 [100,1] obtido na iteração 1
muda para [55,4] na iteração 3 a fim de indicar que foi
encontrada uma rota mais curta que passa pelo nó 4.
Além disso, na iteração 3, o nó 5 tem dois rótulos
alternativos com a mesma distância U5 = 90.
Na iteração 3, o rótulo para o nó 2 passa a ser
permanente.
Iteração 4: Só o nó 3 pode ser alcançado com base no nó
2. Contudo o nó 3 tem um rótulo permanente e não pode
ser rotulado novamente.
A nova lista de rótulos permanece a mesma na iteração 3,
exceto que o rótulo no nó 2 é permanente. Isso deixa o
nó 5 como o único rótulo temporário.
Como o nó 5 não leva a outros nós, seu status é
convertido em permanente, e o processo termina.
O caminho mais curto entre o nó 1 e qualquer outro é
determinado começando no nó de destino desejado e
percorrendo a rota inversa a partir desse ponto, usando a
informação dada pelos rótulos permanentes.
Por exemplo, a seguinte sequencia determina a rota mais
curta do nó 1 ao nó 2.
(2)  [55,4]  (4)  [40,3]  (3)  [30,1]  (1)
Exercício: A rede da figura abaixo fornece as distâncias
em milhas entre pares de cidades. Use o algoritmo de
Dijkstra para achar o caminho mais curto entre as
seguintes cidades:
a.) Cidades 1 e 8
b.) Cidades 1 e 6
5.2 Fluxo máximo
Dado um arco (i,j) com i < j, usamos a notação (Cij,
Cji) para representar as capacidades de fluxo nas
duas direções i  j e j  i , respectivamente,
conforme apresentado na figura abaixo.
Cij
i
Cji
j
Cij: arco de fluxo I  J
Cji: arco de fluxo J  I
Define-se um corte como um conjunto de arcos, que
quando eliminados da rede, causará um rompimento
total do fluxo entre o nó de origem e o nó
sorvedouro.
A capacidade do corte é igual à soma das
capacidades de seus arcos.
Entre todos os possíveis cortes na rede, o que tiver a
menor capacidade dá o fluxo máximo da rede.
Considere a rede da figura abaixo. As capacidades
bidirecionais são mostradas nos respectivos arcos
usando a convenção apresentada anteriormente.
A figura apresenta 3 cortes cujas capacidades estão
apresentadas a seguir:
Corte 2
0
20
4
Corte 3
Corte 1
5
10
1
0
0
30
5
0
20
30
0
2
40
0
0
10
3
20
Corte
Arcos Associados
Capacidades
1
(1,2), (1,3), (1,4)
20+30+10 = 60
2
(1,3), (1,4), (2,3), (2,5) 30+10+40+30 = 110
3
(2,5), (3,5), (4,5)
30+20+20 = 70
O fluxo máximo da rede não pode ultrapassar 60
unidades. Para determinar o fluxo máximo é
necessário enumerar todos os cortes !
Em uma rede de grande porte este procedimento
pode ficar inviável. Portanto, é necessário de se
desenvolver um algorítmo que torne o processo
eficiente !
Algorítmo de fluxo máximo
Este algoritmo é baseado em achar rotas de
passagem com fluxo líquido positivo entre os nós de
origem e sorvedouro. Cada rota compromete parte
ou toda a capacidade de seus arcos ao fluxo da rede.
Dada a figura anterior, determine o fluxo máximo na
rede.
Etapas do algoritmo:
Iteração 01: Iguale as capacidades residuais iniciais
às capacidades Iniciais ( Cij, Cji);
Etapa 01: Determine a1 = infinito, e rotule o nó 1
com [infinito,--]. Determine i = 1;
Etapa 2: S1 = {2,3,4} (diferente de vazio)
Etapa 3: K =3, por que C13 = max {C12, C13, C14} =
Max { 20,30,10} = 30. Determine a3 = C13 = 30, e
rotule o nó 3 com [30,1]. Determine i=3 e repita a
etapa 2;
Etapa 2: S3 = {4,5}
Etapa 3: K = 5 e a5 = C35 = max {10,20} = 20. Rotule o
nó 5 com [20,3]. Uma rota de passagem é obtida. Vá
para a etapa 5.
Etapa 5: A rota de passagem é determinada pelos
rótulos que iniciam no nó 5 e percorrem a rota
inversa até o nó 1, isto é:
(5)  [20,3]  (3)  [30,1]  (1)
Assim, N1 = {1,3,5} e f1 = min {a1,a2,a5} =
{infinito,30,20} = 20. As capacidades residuais ao
longo da rota N1 são:
(C13, C31) = (30-20, 0 + 20) = (10,20)
(C35, C53) = (20-20, 0 +20) = (0,20)
Iteração 2:
Etapa 1. Determine a1 = infinito, e rotule o nó 1 com
[infinito, --]. Determine i = 1;
Etapa 2: S1 = {2,3,4};
Etapa 3: K=2 e a2 = C12 = max {20,10,10} = 20.
Determine i=2 e repita a etapa 2;
Etapa 2: S2 = {3,5}
Etapa 3: K = 3 e a3 = C23 = 40. Rotule o nó 3 com
[40,2]. Determine i = 3 e repita a etapa 2.
Etapa 2: S3 = {4} . Observe que C35 = 0, portanto, o
nó 5 não pode ser incluído em S3;
Etapa 3: k = 4 e a4 = c34 = 10. Rotule o nó 4 com
[10,3]. Determine i = 4 e repit a etapa 2;
Etapa 2: S4 = {5} . Observe que os nós 1 e 3 estão
rotulados, portanto, não podem ser incluídos em S4;
Etapa 3: K = 5 e a5 = c45 = 20. Rotule o nó 5 com
[20,4]. Foi conseguida uma rota de passagem. Vá
para a etapa 5.
Etapa 5: N2 = {1,2,3,4,5} e
f2 = min {infinito,20,40,10,20} = 10.
As capacidades residuais ao longo da rota de N2 são:
(C12,C21) = (20-10,0+10) = (10,10)
(C23,C32) = (40-10, 0+10) = (30,10)
(C34,C43) = (10-10, 5+10) = (0,15)
(C45,C54) = (20-10, 0+10) = (10,10)
Iteração 3
Etapa 1: Determine a1 = infinito e rotule o nó 1 com
[infinito, --]. Determine i=1.
Etapa 2: Si = {2,3,4}
Etapa 3: K =2 e a2 = C12 = max[10,10,10] = 10.
Empates são decididos aleatoriamente. Vamos
rotular o nó 2 com [10,1]. Determine i=2 e repetir a
etapa 2.
Etapa 2: S2 = {3,5}
Etapa 3: K=3 e a3 = C23 = 30. Rotule o nó 3 com
[30,2]. Determine i = 3 e repita a etapa 2.
Etapa 2: S3 = vazio, porque C34 = C35 = 0. Vá para a
etapa 4ª fim de percorrer a rota inversa.
Etapa 3: Rota inversa. O rótulo [30,2] no nó 3 dá o nó
imediatamente precedente r =2. Elimine o nó 3 de
qualquer consideração nessa iteração, cancelando-o.
Determine i = r = 2, e repita a etapa 2.
Etapa 2: S2 = {5}. Observe que o nó 3 foi eliminado
na etapa da rota inversa.
Etapa 3: k = 5 e a5 = C25 = 30. Rotule o nó 5 com
[30,2]. Foi conseguida uma rota de passagem. Vá
para a etapa 5.
Etapa 5: N3 = {1,2,5} e C5 = min {infinito, 10,30} = 10.
As residuais ao longo da rota de N3 são:
(C12,C21) = (10-10,10+10) = (0,20)
(C25, C52) =(30 -10 , 0+10) = (20,10)
Iteração 4. Esssa iteração dá N4 = {1,3,2,5} com
f4=10.
Iteração 5. Essa iteração dá N5 = {1,4,5} com f5 = 10
Iteração 6.
Todos os arcos eu partem do nó 1 tem reisduais
zero. Portanto, não há mais nenhuma rota de
passagem possível. Retornar à etapa 6 para
determinar a solução:
Etapa 6: Fluxo máximo na rede é:
F = f1 + f2 + ... + f5 = 20+10+10+10+10 = 60.
contin
Formalização do algorítimo:
Considere o arco (i,j) inicialmente com capacidade
(Cij, Cji). À medida que porções destas capacidades
são comprometidas ao fluxo no arco, as capacidades
residuais (ou capacidades restantes) do arco são
atualizadas. Usando a notação (cij,cji) para
representar essas capacidades residuais.
Para um nó j que recebe fluxo do nó i, anexamos um
rótulo [aj,i], no qual aj é o fluxo do nó i ao nó j.
Assim, as etapas do algoritmo são resumidas da
maneira a seguir:
Etapa 1: Para todos os arcos (i,j) iguale a capacidade
residual à capacidade inicial, isto é:
(cij, cji) = (Cij, Cji).
Seja a1 = infinito e rotule o nó de origem com
[infinito,--]. Determine i = 1 passe para a etapa 2.
Etapa 2: Determine Si, que representa o conjunto de
nós j não rotulados que podem ser alcançados
diretamente do nó i por arcos com residuais
positivos, isto é cij > 0, para todo j E Si. Se Si for
diferente de zero, vá para a etapa 3. Caso contrário,
vá par a etapa 4.
Etapa 3: Determine k E Si, tal que:
Cik = Max {cij}, j E Si
Determine ak = cik e rotule o nó k com [ak,i]. Se k = n, o
nó sorvedouro foi rotulado e foi encontrada uma rota de
passagem. Vá para a etapa 5. Caso contrário, determine i
= k e vá para a etapa 2.
Etapa 4: (percorrer a rota inversa). Se i = 1, nenhuma
rota de passagem é possível, vá para a etapa 6. Caso
contrário, determine que r seja o nó que foi rotulado
imediatamente antes do nó atual i e elimine i do
conjunto de nos adjacentes a r. Determine i=r e vá
para a etapa 2.
Etapa 5: (determinação das capacidades residuais).
Defina os nós da p-ésima rota de passagem de nó de
origem ao nó sorvedouro n como:
Np = (1, K1, K2, ...,n). Então o fluxo máximo ao longo
da rota é calculado por:
Fp = min {a1,ak1,ak2,...,an}
A capacidade residual de cada arco ao longo da rota
de passagemé reduzida de Fp, na direção do fluxo e
aumentada de Fp, na direção contrária; isto é, para
os nós i e j na rota, o fluxo residual é alterado do
atual para:
(a) ( cij – fp, cji + fp) se o fluxo for de i para j;
(b) (cij + fp, cji – fp) se o fluxo for de j para i.
Reinstale quaisquer nós que foram eliminados na etapa 4.
Determine i = 1 e retorne à etapa 2 para tentar uma nova
rota de passagem.
Exercícios:
1.) Determine o fluxo máximo para a rede da figura
abaixo:
2.) Três refinarias enviam um produto à base de
gasolina a dois terminais de distribuição por meio de uma
rede de tubulações. Qualquer demanda que não puder
ser satisfeita pela rede é adquirida de outras fontes. A
rede de tubulações é atendida por três estações de
bombeamento, como mostrado na figura abaixo. O
produto flui pela rede na direção mostrada pelas setas. A
capacidade de cada segmento de tubulação (mostrada
diretamente nos arcos) é dada em milhões de barris por
dia.
Estações
bombeamento
Refinarias
1
terminais
20
10
7
4
10
10
2
50
50
6
20
30
20
20
5
30
3
8
15
Determine o seguinte:
a.) A produção diária em cada refinaria que combina
com a máxima capacidade da rede;
b.) A demanda diária em cada terminal que combina
com a máxima capacidade da rede;
c.) A capacidade diária de cada bomba que combina
com a máxima capacidade da rede.
Obs: A solução do problema proposto requer equipar a
rede com uma única origem e um único sorvedouro
usando arcos unidirecionais de capacidade infinita
representados na figura abaixo e grifados em vermelho:
Estações
bombeamento
Refinarias
1
terminais
20
10
7
4
20
10
10
80
0
2
60
50
50
6
9
20
30
20
20
5
15
50
30
3
15
8
3.) Use o algoritmo de Dijkstra para achar o caminho
mais curto entre o nó 1 e todos os outros da rede da
figura abaixo:
6
6
2
7
5
1
2
7
4
4
2
7
6
6
1
5
3
9
1
7
5
3
7
4.) De três depósitos A, B e C, dispondo-se
respectivamente de 20,10 e 35 toneladas de um dado
produto, pretende-se fazer chegar a três destinos D,E e
F, respectivamente, 25, 20 e 20 toneladas do produto. As
disponibilidades de transporte via caminhão entre as
localidades é dada na tabela abaixo. Estabeleça o melhor
plano de transportes.
5.) Dado o grafo abaixo determinar o fluxo máximo
entre os nós 1 e 6
v