Indutores e Indutância

Eletromagnetismo
Indutores e Indutância
Eletromagnetismo » Indutores e Indutância
Introdução
Indutores são elementos muito úteis, pois com eles podemos armazenar energia de natureza
magnética em um circuito elétrico. Sob este aspecto, ele tem algo em comum com um capacitor.
Trata-se, portanto, de elemento ativo de um circuito no qual ele está inserido.
Podemos definir indutor como um elemento de um circuito contendo dois terminais, e composto
por N enrolamentos. Quando os enrolamentos são feitos de fios ideais, sem resistência elétrica, o
indutor é considerado ideal. Seu papel é produzir indutância, definida como uma propriedade do
indutor, mediante a qual uma corrente que o percorre, variando com o tempo, leva a uma tensão
agindo sobre ele. Essa tensão será indicada pela letra ε e receberá o nome de tensão auto-induzida.
Um indutor comum é representado pelo primeiro símbolo abaixo:
Figura 1: Tipos de indutores e sua representação.
Os indutores são caracterizados por uma grandeza física denominada indutância (ou coeficiente
de autoindutância), representada pela letra L. Veremos que tal grandeza é, em última análise, determinada pela geometria do indutor, além de outros parâmetros, como o número de enrolamentos.
Veremos que a indutância aumenta consideravelmente com o número de espiras numa bobina.
De particular relevância no sentido de amplificar seu efeito como elemento ativo do circuito, a
indutância de uma bobina, por exemplo, depende do material magnético que constitui seu núcleo.
Como é sabido, alguns materiais magnéticos (aqueles dotados de alta permeabilidade magnética)
realçam o campo magnético. Assim, a indutância é aumentada por um fator dado pela permeabilidade relativa do material do núcleo.
Os indutores podem ser construídos de forma a terem uma indutância variável. A figura 000
ilustra a representação desses tipos de indutores.
Outros coeficientes importantes são aqueles relativos à indução mútua. Ela ocorre quando
circuitos interagem entre si. Neste caso, os coeficientes importantes são os coeficientes de indutância
1
Eletromagnetismo » Indutores e Indutância
2
mútua, que serão representados por uma matriz M, cujo elemento de matriz Mij representa a
indutância mútua entre o circuito i e o circuito j.
Como a indução é um fenômeno comum a todo circuito, ele é indissociável do mesmo. Ou seja,
de um ponto de vista rigoroso, devemos sempre associar uma indutância a um circuito.
Figura 2: Indutores podem ser elementos bem simples, como, por exemplo, uma espira
ou um arranjo de várias delas, no caso das bobinas.
Auto-Indução e Coeficiente de Indutância
Consideremos o caso de um circuito isolado pelo qual circula uma corrente elétrica I que varia
com o tempo. Ou seja:
I = I(t)
( 1 )
Tal corrente produzirá um campo magnético que varia com o tempo e, consequentemente, o
circuito fica imerso nesse campo produzido por sua própria corrente elétrica. Tendo em vista que a
corrente é variável, o mesmo ocorre com o campo magnético produzido por essa corrente. Como
resultado, o fluxo desse campo através do circuito será variável. Ou seja,
Φ = Φ(t)
( 2 )
Eletromagnetismo » Indutores e Indutância
3
De acordo com a lei de Faraday, um condutor percorrido por uma corrente variável experimenta
uma indução magnética que, por sua vez, leva ao surgimento de uma corrente elétrica induzida.
Para determinar seu sentido, devemos utilizar a lei de Lenz.
O fato é que o condutor fica imerso nesse campo magnético produzido por sua própria corrente.
Esse campo produz no próprio condutor um fluxo Φ (Figura 000). Como a corrente i varia, o seu
campo também será variável e, por consequência, o fluxo Φ será variável. Nessas circunstâncias, o
condutor, sendo atravessado por um fluxo variável, sofre indução eletromagnética. Portanto, como
consequência da corrente i ser variável, surge no condutor uma corrente elétrica induzida. Esse
fenômeno é denominado autoindução.
Ocorre autoindução magnética sempre que um condutor leva a uma indução magnética sobre
si mesmo. Isso ocorre sempre que a corrente no circuito varia com o tempo.
Portanto, estamos tratando de um caso de autoindução. Ou seja, uma força eletromotriz induzida pelo circuito sobre si mesmo.
Nesse caso o fluxo do campo elétrico através do circuito dependerá do tempo apenas através da
corrente elétrica. Logo, podemos escrever:
ε=−
dΦ
d Φ dI
=−
dt
dI dt
( 3 )
Essa tensão é conhecida como tensão auto-induzida.
Ao primeiro coeficiente do lado direito dessa expressão, damos o nome de coeficiente de
indutância mútua ou, simplesmente, indutância, representada pela letra L. Assim, temos:
L≡
dΦ
dI
( 4 )
Tendo em vista a dependência linear do fluxo com a corrente original, a corrente que percorre o
condutor, podemos definir a indutância como o quociente entre o fluxo e a corrente:
L≡
Φ
I
( 5 )
No sistema SI, a unidade de fluxo é o Weber. Tendo em vista que a unidade do campo elétrico
no mesmo sistema é o Tesla (T), tem-se que:
1Weber = T.m2
( 6 )
Figura 3
Eletromagnetismo » Indutores e Indutância
4
A indutância é medida na unidade Henry, símbolo H.
1weber
T ⋅ m2
1Henry = 1H =
=1
ampére
A
( 7 )
Como veremos nos próximos exemplos, o coeficiente de autoindutância envolve certas características
do indutor, como sua geometria, número de enrolamentos e o material do núcleo de uma bobina.
Utilizando o coeficiente de indutância, escrevemos a Lei de Faraday para a tensão autoinduzida
da seguinte forma:
ε = −L
dI
dt
Figura 4: A indutância pode ser aumentada por meio do uso de um
núcleo de ferro.
exercícios resolvidos 
( 8 )
Eletromagnetismo » Indutores e Indutância
5
Abertura e Fechamento de um Circuito
Um dos efeitos da autoindução, sendo perceptível e mensurável, é aquele que acontece quando
abrimos e fechamos um circuito. Para entendê-lo, é importante lembrar que, nos casos de corrente
variável, se a corrente elétrica I que percorre o circuito estiver diminuindo (dI/dt < 0), a corrente
resultante do processo de autoindução, a corrente I′ tem o mesmo sentido que ela. No entanto,
se a corrente estiver numa fase crescente (dI/dt > 0), isto é, aumentando, a corrente decorrente
do processo de autoindução (I′) tem sentido oposto a ela. Tal regra decorre do uso da Lei de Lenz.
Pode-se constatar que, quando fechamos um circuito, a corrente não atinge imediatamente o valor
final I. Um comportamento típico da corrente em função do tempo é ilustrado na Figura 000. Ou seja,
a corrente não atinge o valor esperado imediatamente, mas o faz depois de um intervalo de tempo
Δt. O intervalo de tempo depende da indutância do circuito. Este fenômeno é mais pronunciado para
valores elevados da indutância (quando nele inserimos uma bobina, por exemplo).
Uma vez que a corrente varia, no caso da abertura, ela está aumentando com o tempo, e apenas
durante o intervalo de tempo Δt, o fenômeno da autoindução tem exatamente essa duração. O fato
é que, nesse caso, a corrente é uma soma de correntes geradas por dois efeitos. A corrente gerada
quando abrimos o circuito argumentar e a corrente gerada pela autoindução.
Quando fechamos um circuito, ocorre um fenômeno análogo, muitas vezes bastante pronunciado. Um gráfico típico, nesse caso, é aquele esboçado na Figura 000. Novamente, como no caso
da abertura do circuito, a corrente não cai imediatamente a zero. Ao fechar o circuito, surge uma
corrente induzida. Essa corrente, de acordo com a Lei de Lenz, atua no sentido de elevar a corrente
elétrica. A soma dos dois efeitos, corrente desligada mais a corrente induzida, é a elevação do valor
da corrente elétrica por um pequeno lapso de tempo, para depois ir reduzindo até atingir o valor
nulo. Este efeito pode ser bastante pronunciado gerando, em alguns casos, faíscas na chave .
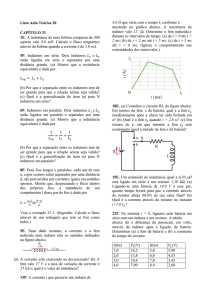
Figura 5: Comportamento típico da corrente como
função do tempo quando abrimos um circuito.
Figura 6:. Ilustração do comportamento da
corrente no circuito quando ele é fechado.
Eletromagnetismo » Indutores e Indutância
6
Indutância Mútua
Em muitas situações de interesse físico, os circuitos podem interagir entre si. E isso acontece
quando circuitos próximos têm suas correntes variando com o tempo. Nesse caso, os campos
magnéticos através deles, ou de um deles, variam com o tempo.
Consideremos o caso em que temos N circuitos, os quais serão designados pelos índices 1, 2, ...N; e que
um certo número, n, desse circuitos tenham correntes variando com o tempo. Essa variação das correntes
elétricas acarretará uma variação no fluxo do campo elétrico através dos demais circuitos. Assim, o fluxo
no i-ésimo circuito, aqui designado por Φ, poderá ser escrito como uma soma sobre n circuitos:
n
Φi = ∑ Φi j
( 9 )
j =1
No caso em que todos os N circuitos tenham correntes variáveis, escrevemos:
N
Φi = ∑ Φi j
( 10 )
j =1
Φij é o fluxo do campo magnético através do i-ésimo circuito gerado pela variação da corrente
no j-ésimo circuito. Ou seja, o fluxo no i-ésimo circuito é a somatória dos fluxos associados aos
campos magnéticos produzidos pelos demais circuitos (e o dele mesmo, como visto antes).
O campo magnético produzido pelo j-ésimo circuito depende da corrente no mesmo (a corrente Ij).
Assim, podemos escrever para a taxa de variação do fluxo:
N dΦ
d Φi
i j dI j
=∑
dt
dt
j =1 dI j
( 11 )
Se houver variação da corrente em apenas um dos circuitos, rotulado com o índice 1, a taxa
de variação do fluxo nos demais sistemas e no próprio circuito é dada como função da taxa de
variação da corrente neste circuito. Assim, escrevemos:
d Φ i d Φ i j dI1
=
dI1 dt
dt
( 12 )
Eletromagnetismo » Indutores e Indutância
7
Denomina-se coeficiente de indutância mútua Mij o coeficiente dado pela taxa de variação:
M ij =
d Φi j
( 13 )
dI j
Nessa notação, podemos escrever o coeficiente de autoindutância do i-ésimo circuito (Li) como
sendo um dos coeficientes acima. Isto é, nessa notação, escrevemos :
Li = Mii
( 14 )
Tendo em vista a dependência linear do fluxo com a corrente, podemos escrever, de forma
simplificada:
M ij =
Φi j
( 15 )
Ij
Em termos dos coeficientes de indutância mútua, podemos escrever a força eletromotriz induzida
no i-ésimo circuito como sendo dada pela somatória:
N
εi = −∑ M ij
j =1
dI j
dt
( 16 )
A famosa experiência de Faraday, colocando duas bobinas próximas uma da outra, se encaixa
nesse contexto. A força eletromotriz na segunda bobina é proporcional à taxa de variação da
corrente elétrica na primeira bobina. Ou seja:
ε 2 = −M 21
dI1
dt
( 17 )
A constante nessa relação linear é o coeficiente de indutância mútua, que envolve características
dos dois sistemas. Como regra geral, podemos escrever:
M
=
M
=
k L1 L2
21
12
Sendo que L1, L2 são as indutâncias de cada uma das bobinas.
( 18 )
Eletromagnetismo » Indutores e Indutância
8
Figura 7: esquema da experiência de Faraday
Fórmula de Neumann
É possível escrever uma expressão bastante geral para a indutância mútua e a autoindutância em
termos de uma integral dupla de caminhos envolvendo os circuitos. Essa é a fórmula de Neumann.
Lembrando que força eletromotriz sobre o i-ésimo circuito pode ser escrita como:
εi = −
d Φi
d   
= −  ∫∫ B ⋅ dS 
dt
dt  Si

( 19 )
O campo magnético pode ser escrito como o rotacional do potencial vetor:


B = ∇× A
( 20 )
Substituindo a expressão acima em (000) e utilizando o teorema de Stokes, podemos escrever
a força eletromotriz como uma integral de caminho do potencial vetor. Tal caminho Γ ao longo do
i-ésimo circuito. Isto é:
εi = −
d  
 ∫ A ⋅ dli 
dt  
Γi
( 21 )
Eletromagnetismo » Indutores e Indutância
9
A contribuição para o potencial vetor associada ao j-ésimo circuito é:
1
Aj ( r ) = µ 0 I j ∫ dl ′j
′
Γj r − r
( 22 )
Portanto, a força eletromotriz sobre o i-ésimo circuito poderá ser escrita como uma soma da forma:
N
εi = −∑ µ 0
j =1
dI j 

∫
dt  Γi

∫
Γj

dl
i ⋅ dl j 
ri − rj′

1
( 23 )
Conclui-se assim, utilizando-nos das expressões (000) e (000), que o coeficiente de indutância
mútua entre os circuitos i e j é dada pela dupla integral de caminho:
M ij = −µ 0 ∫
Γi
∫
Γj
1
dli ⋅ dl j
ri − rj′
( 24 )
Enquanto que expressão análoga vale para o coeficiente de autoindutância. Para o i-ésimo
circuito, escrevemos:
Li = − µ0 ∫
Γi
Figura 8
∫
Γj
1
dli ⋅ dl ′j
ri − rj′
( 25 )
Eletromagnetismo » Indutores e Indutância
10
Energia armazenada num sistema de Indutores
Um indutor armazena energia de natureza magnética. Ela fica distribuída no espaço e concentrada nos pontos próximos do indutor. Ou seja, a densidade de energia ρM é maior nos pontos
próximos do indutor. Ela é dada pela expressão:
ρ M ( x, y , z ) =

1 2
B ( x, y , z )
2µ
( 26 )
Em que B é o campo magnético na região na qual o indutor está inserido.
A energia armazenada pode ser expressa em termos da corrente e da indutância. Para isso,
determinamos a variação de energia
quando deslocamos uma quantidade de carga dq pelo indutor.

dl
Para um deslocamento virtual , temos que a força à qual devemos nos opor é a força elétrica:

F = −dqE
( 27 )
A energia é dada, portanto, pela integral de caminho:
dU = − dq ∫ E idl = − dqε
( 28 )
Lembrando que I = dq/dt, a expressão acima se escreve como:
dE = dq
dI
dI
d  LI 2 
L=I
Ldt = 
 dt
dt
dt
dt  2 
( 29 )
Conclui-se daí que a potência suprida pelo indutor é:
dI
I vI
=
P L=
dt
( 30 )
E que a energia armazenada é dada por:
E=
LI 2
2
( 31 )1
Eletromagnetismo » Indutores e Indutância
11
No caso de vários indutores, a energia é dada pela expressão:
N N
1
E = ∑ ∑ M ij I i I j
i =1 j =1 2
( 32 )
exercícios resolvidos 
Associação de Indutores
Assim como no caso de resistores e capacitores, existem duas formas básicas de associar indutores: em paralelo ou em série.
Associação em série
Nesse tipo de associação, dispomos os indutores de tal forma que o término de um deles coincide com
o início do próximo indutor (vide figura). Ou seja, eles têm terminais que são, dois a dois, em comum.
Figura 9: Indutores em série.
Para um determinado trecho da associação em série (trecho esse fazendo parte, por exemplo,
de um circuito), comprendido, por exemplo, entre dois terminais A e E, trecho esse contendo N
resistores, podemos chegar às seguintes conclusões:
Eletromagnetismo » Indutores e Indutância
12
a. Corrente Elétrica
A corrente elétrica percorrendo tal arranjo é a mesma que passa ao longo de cada um dos
indutores. Ou seja, a corrente que passa pelo primeiro é a mesma que passa pelo segundo e assim
por diante. Isso decorre do princípio de conservação da carga elétrica. Como as cargas não se
acumulam em um indutor e não têm para onde se desviar, o número daquelas que passam pelo
primeiro terminal A é igual ao número das que passam pelo terminal E.
b. Tensões nos Terminais de cada Elemento
As tensões sobre cada um dos indutores são diferentes. Designando as resistências L1, L2,...LN,
respectivamente, dos resistores 1, 2...N, podemos escrever a tensão sobre o EQN indutor como
sendo dada pelo produto:
εj = Lji
( 33 )
ε = εAB + εBC + ..... + εDE
( 34 )
Lembrando que:
Obtemos que a tensão entre os terminais do primeiro e o último resistor é dada pela soma:
N
N
j =1
j =1
ε = ∑ ε j = ∑ L ji
( 35 )
c. Indutor equivalente
Definimos indutor equivalente aquele cuja indutância é equivalente à do conjunto de indutores
em série. Por essa definição, a indutância equivalente é tal a obedecer a relação:
ε = Li
( 36 )
Eletromagnetismo » Indutores e Indutância
13
Da equação (000), segue que:
 N

ε =  ∑ Lj  i
 j =1 
( 37 )
Portanto, a resistência do indutor equivalente é dada pela soma das resistências dos resistores
que compõem o arranjo. Ou seja:
N
L = ∑ Lj
( 38 )
j =1
Associação em Paralelo
Nesse caso, os resistores são dispostos de tal forma que todos eles têm os mesmos terminais.
Podemos pensar esse arranjo como sendo de condutores ligados em dois pontos A e B (vide
Figura 000)
Para um determinado trecho da associação em série (fazendo parte, por exemplo, de um
circuito), comprendido, por exemplo, entre dois terminais A e E, trecho esse contendo N indutores,
podemos chegar às seguintes conclusões:
a.Tensões nos Terminais de Cada Elemento
A tensão sobre cada um dos elementos é a mesma, designada por ε. Podemos escrever a tensão
sobre o j-ésimo indutor como sendo:
εj = ε
( 39 )
b. Corrente Elétrica
A corrente elétrica percorrendo cada um dos resistores dispostos em paralelo é diferente. Designando L1, L2,....LN as indutâncias, respectivamente, dos indutores 1, 2....N, e por i1, i2,....iN as respectivas correntes, podemos escrever a tensão sobre o j-ésimo indutor como sendo dada pelo produto:
ε = Ljij
( 40 )
Figura 10: Indutores em paralelo.
Eletromagnetismo » Indutores e Indutância
14
Portanto, a corrente elétrica no j-ésimo resistor é dada por:
ij =
ε
Lj
( 41 )
A relação acima vale para qualquer um dos elementos que compõem o arranjo em paralelo
c. Indutor equivalente
Consideremos uma corrente elétrica i, que chega ao primeiro terminal comum a todos os indutores. Essa corrente se bifurca, produzindo correntes em cada um deles. De acordo com o princípio
da conservação da carga elétrica, podemos afirmar que
i = i1 + i2 + .... + iN
( 42 )
Definimos capacitor equivalente aquele percorrido pela corrente elétrica i, a corrente total, cuja
indutância é equivalente à do conjunto de indutores em série. Por definição, a indutância equivalente é dada por:
ε = Li = L (i1 + i2 +....+ iN)
( 43 )
Figura 11: Substitui-se um conjunto de indutores
por um que lhe seja equivalente.
Lembrando a relação (000), segue de (000) que:
ε 1 1
1
=  + + ⋅⋅⋅⋅ +
L  L1 L2
LN

ε

( 44 )
Portanto, a indutância do indutor equivalente é dada, em função das indutâncias em série,
pela expressão:
1 N 1 1 1
1 
= ∑ =  + + ⋅⋅⋅⋅ +

L j =1 L j  L1 L2
LN 
( 45 )
Eletromagnetismo » Indutores e Indutância
15
Exercício Resolvido: Auto-indução e coeficiente
de indutância
Exemplo
Determine a indutância de uma bobina toroidal, com N rolamentos, cujo núcleo é constituído de
uma material ferromagnético de permeabilidade μ.
No caso de um Toroide, o campo produzido por uma corrente I que o percorre é tal que o campo
magnético nos pontos externos ao mesmo é nulo. Se o número de enrolamentos for N e o seu
comprimento for l, então no seu interior esse campo é dado por:

N
B = µI eϕ
l
( 46 )
Em que μ é a permeabilidade do material magnético do núcleo.
Tendo em vista que o campo magnético é paralelo à normal de uma espira, o fluxo desse campo
sobre cada uma delas é dado pelo produto da área da secção transversal da espira, A, pelo campo
magnético. Ou seja:
Φ1 = B0 A = µI
N
A
l
( 47 )
Portanto, o fluxo do campo elétrico, quando consideramos os N enrolamentos (N espiras), é
dado por:
Φ = N Φ1 = NB0 A = µIA
N2
L
( 48 )
Consequentemente, a indutância do enrolamento definida por:
L=
Φ N Φ1
=
I
I
( 49 )
nos leva ao resultado:
L = µA
N2
l
( 50 )
Eletromagnetismo » Indutores e Indutância
16
O mesmo resultado vale para uma bobina constituída por um enrolamento na forma de
solenoide, desde que admitamos que o resultado para um solenoide infinito se aplica também para
um solenoide de comprimento l.
Figura 12: Um indutor toroidal
contendo N enrolamentos
Eletromagnetismo » Indutores e Indutância
17
Exercício Resolvido: Energia armazenada num sistema
de indutores
Exemplo
Determinar a energia e os coeficientes de autoindução e indução mútua no caso de dois circuitos
toroidais, tendo em vista que um tem N1 enrolamentos, enquanto o outro tem N2 enrolamentos.
Resolução
O campo magnético produzido pelos dois enrolamentos, baseado no princípio da superposição,
é dado pela soma:
 
N
N 
B =  µI1 1 + µI 2 2  eϕ
l
l 

( 51 )
Portanto, a densidade de energia magnética é uniforme, concentrada no interior do toroide e
dada por:
ρM =
1 2 µ
B = 2 ( I1 N1 + I 2 N 2 ) 2
µ
l
( 52 )
A energia eletromagnética total é dada por:
E = ρM V =
1 2
BV
µ
( 53 )
Em que V é o volume interno do Toroide. Sendo sua área transversal dada por A e seu comprimento sendo l, tal volume é dado por:
V = Al
( 54 )
Portanto, de (000) e (000), concluímos que a energia desses dois circuitos é dada por:
E=

µA  I12 N12 + I 2 2 N 2 2
+ I1 N1 I 2 N 2 

l 
2

( 55 )
Eletromagnetismo » Indutores e Indutância
18
Expressão a partir da qual inferimos os seguintes resultados:
µAN12
L1 = M 11 =
l
µAN 2 2
L2 = M 22 =
l
µAN1 N 2
M 12 = M 21 =
= L2 L1
l
Figura 13: Dois indutores toroidais contendo N1 e N2 enrolamentos.
( 56 )
Eletromagnetismo » Indutores e Indutância
19
Como usar este ebook
Orientações gerais
Caro aluno, este ebook contém recursos interativos. Para prevenir problemas na utilização desses recursos, por favor acesse o arquivo
utilizando o Adobe Reader (gratuito) versão 9.0 ou mais recente.
Botões
Indica pop-ups com mais informações.
Ajuda (retorna a esta página).
Sinaliza um recurso midiático (animação, áudio etc.) que pode
estar incluído no ebook ou disponível online.
Créditos de produção deste ebook.
Indica que você acessará um outro trecho do material.
Quando terminar a leitura, use o botão correspondente (  )
para retornar ao ponto de origem.
Bons estudos!
Eletromagnetismo » Indutores e Indutância
Créditos
Este ebook foi produzido pelo Centro de Ensino e Pesquisa Aplicada (CEPA), Instituto de Física da Universidade de São Paulo (USP).
Autoria: Gil da Costa Marques.
Revisão Técnica e Exercícios Resolvidos: Paulo Yamamura.
Coordenação de Produção: Beatriz Borges Casaro.
Revisão de Texto: Marina Keiko Tokumaru.
Projeto Gráfico e Editoração Eletrônica: Daniella de Romero Pecora, Leandro de Oliveira e Priscila Pesce Lopes de Oliveira.
Ilustração: Alexandre Rocha, Aline Antunes, Benson Chin, Camila Torrano, Celso Roberto Lourenço, João Costa, Lidia Yoshino,
Maurício Rheinlander Klein e Thiago A. M. S.
Animações: Celso Roberto Lourenço e Maurício Rheinlander Klein.
20