1. Para a distribuição normal, qual é a probabilidade de uma

UNIVERSIDADE FEDERAL DE SANTA CATARINA
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE PRODUÇÃO
ÁREA DE CONCENTRAÇÃO: SISTEMA DE PRODUÇÃO
DISCIPLINA: CONTROLE ESTATÍSTICO DE QUALIDADE
PROFESSOR: ROBERT WAYNE SAMOHYL
MESTRANDO: MARCIO EVANDRO CARDOSO
Capítulo 3- As distribuições de probabilidade mais importantes em controle estatístico
de qualidade (CEQ): variáveis mensuráveis
Questões para discussão e exercícios
1. Para a distribuição normal, qual é a probabilidade de uma mensuração ficar no
máximo a distância de 1,5 desvios padrão da média? Sua resposta pode ser
aproximada.
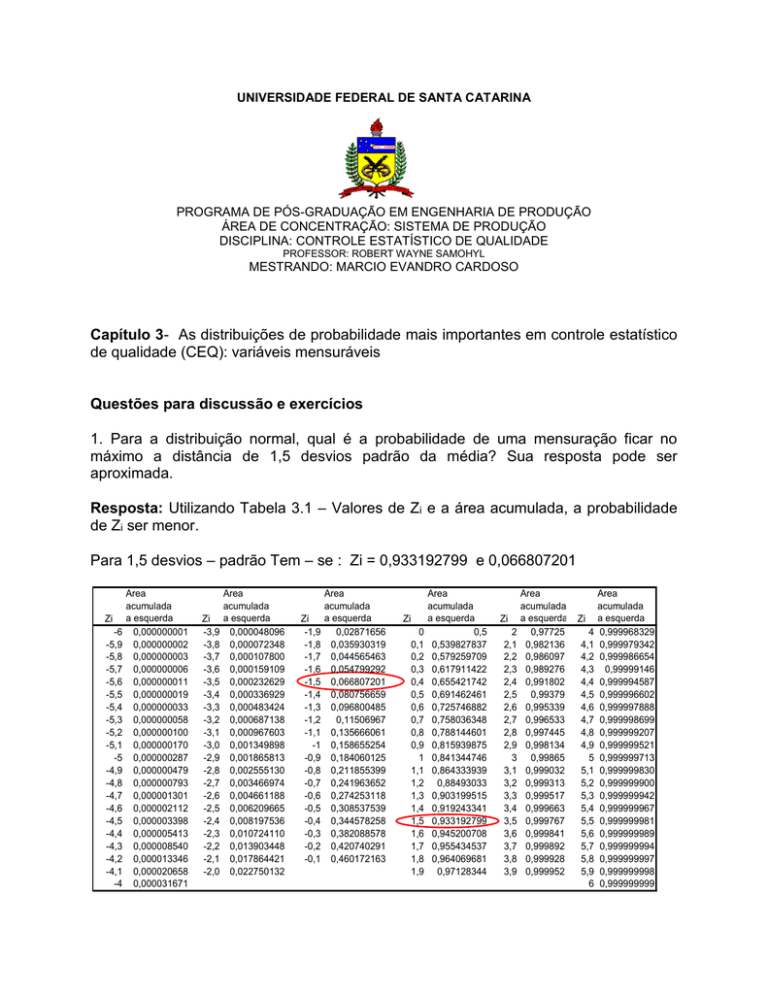
Resposta: Utilizando Tabela 3.1 – Valores de Zi e a área acumulada, a probabilidade
de Zi ser menor.
Para 1,5 desvios – padrão Tem – se : Zi = 0,933192799 e 0,066807201
Zi
-6
-5,9
-5,8
-5,7
-5,6
-5,5
-5,4
-5,3
-5,2
-5,1
-5
-4,9
-4,8
-4,7
-4,6
-4,5
-4,4
-4,3
-4,2
-4,1
-4
Area
acumulada
a esquerda
0,000000001
0,000000002
0,000000003
0,000000006
0,000000011
0,000000019
0,000000033
0,000000058
0,000000100
0,000000170
0,000000287
0,000000479
0,000000793
0,000001301
0,000002112
0,000003398
0,000005413
0,000008540
0,000013346
0,000020658
0,000031671
Zi
-3,9
-3,8
-3,7
-3,6
-3,5
-3,4
-3,3
-3,2
-3,1
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
-2,0
Area
acumulada
a esquerda
0,000048096
0,000072348
0,000107800
0,000159109
0,000232629
0,000336929
0,000483424
0,000687138
0,000967603
0,001349898
0,001865813
0,002555130
0,003466974
0,004661188
0,006209665
0,008197536
0,010724110
0,013903448
0,017864421
0,022750132
Zi
-1,9
-1,8
-1,7
-1,6
-1,5
-1,4
-1,3
-1,2
-1,1
-1
-0,9
-0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
Area
acumulada
a esquerda
0,02871656
0,035930319
0,044565463
0,054799292
0,066807201
0,080756659
0,096800485
0,11506967
0,135666061
0,158655254
0,184060125
0,211855399
0,241963652
0,274253118
0,308537539
0,344578258
0,382088578
0,420740291
0,460172163
Zi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
Area
acumulada
a esquerda
0,5
0,539827837
0,579259709
0,617911422
0,655421742
0,691462461
0,725746882
0,758036348
0,788144601
0,815939875
0,841344746
0,864333939
0,88493033
0,903199515
0,919243341
0,933192799
0,945200708
0,955434537
0,964069681
0,97128344
Zi
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
Area
acumulada
a esquerda
0,97725
0,982136
0,986097
0,989276
0,991802
0,99379
0,995339
0,996533
0,997445
0,998134
0,99865
0,999032
0,999313
0,999517
0,999663
0,999767
0,999841
0,999892
0,999928
0,999952
Zi
4
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6
Area
acumulada
a esquerda
0,999968329
0,999979342
0,999986654
0,99999146
0,999994587
0,999996602
0,999997888
0,999998699
0,999999207
0,999999521
0,999999713
0,999999830
0,999999900
0,999999942
0,999999967
0,999999981
0,999999989
0,999999994
0,999999997
0,999999998
0,999999999
Para encontrar a probabilidade de uma mensuração ficar no máximo à distância
de 1,5 desvio-padrão da média subtraímos os valores Zi encontrados
P= 0,933192799-0,066807201
P= 0,866 ou seja 86,6% de probabilidade
Representando Graficamente:
Distribuição normal 1,5 desvio padrão
86,66%
6,68%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
2. Para mensurações que seguem a distribuição normal, num total de 10.000
mensurações, quantas vão ficar no máximo a distância de 2,5 desvios padrão da
média? Sua resposta pode ser aproximada.
Resposta: Utilizando Tabela 3.1 – Valores de Zi e a área acumulada, a probabilidade
de Zi ser menor.
Para 2,5 desvios – padrão Temos : Zi = 0,99379 e 0,006209665
Zi
-6
-5,9
-5,8
-5,7
-5,6
-5,5
-5,4
-5,3
-5,2
-5,1
-5
-4,9
-4,8
-4,7
-4,6
-4,5
-4,4
-4,3
-4,2
-4,1
-4
Area
acumulada
a esquerda
0,000000001
0,000000002
0,000000003
0,000000006
0,000000011
0,000000019
0,000000033
0,000000058
0,000000100
0,000000170
0,000000287
0,000000479
0,000000793
0,000001301
0,000002112
0,000003398
0,000005413
0,000008540
0,000013346
0,000020658
0,000031671
Zi
-3,9
-3,8
-3,7
-3,6
-3,5
-3,4
-3,3
-3,2
-3,1
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
-2,0
Area
acumulada
a esquerda
0,000048096
0,000072348
0,000107800
0,000159109
0,000232629
0,000336929
0,000483424
0,000687138
0,000967603
0,001349898
0,001865813
0,002555130
0,003466974
0,004661188
0,006209665
0,008197536
0,010724110
0,013903448
0,017864421
0,022750132
Zi
-1,9
-1,8
-1,7
-1,6
-1,5
-1,4
-1,3
-1,2
-1,1
-1
-0,9
-0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
Area
acumulada
a esquerda
0,02871656
0,035930319
0,044565463
0,054799292
0,066807201
0,080756659
0,096800485
0,11506967
0,135666061
0,158655254
0,184060125
0,211855399
0,241963652
0,274253118
0,308537539
0,344578258
0,382088578
0,420740291
0,460172163
Zi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
Area
acumulada
a esquerda
0,5
0,539827837
0,579259709
0,617911422
0,655421742
0,691462461
0,725746882
0,758036348
0,788144601
0,815939875
0,841344746
0,864333939
0,88493033
0,903199515
0,919243341
0,933192799
0,945200708
0,955434537
0,964069681
0,97128344
Zi
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
Area
acumulada
a esquerda
0,97725
0,982136
0,986097
0,989276
0,991802
0,99379
0,995339
0,996533
0,997445
0,998134
0,99865
0,999032
0,999313
0,999517
0,999663
0,999767
0,999841
0,999892
0,999928
0,999952
Zi
4
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6
Area
acumulada
a esquerda
0,999968329
0,999979342
0,999986654
0,99999146
0,999994587
0,999996602
0,999997888
0,999998699
0,999999207
0,999999521
0,999999713
0,999999830
0,999999900
0,999999942
0,999999967
0,999999981
0,999999989
0,999999994
0,999999997
0,999999998
0,999999999
Para encontrar a probabilidade de uma mensuração ficar no máximo à distância
de 2,5 desvio-padrão da média para uma população de 10.000 mensurações deve-se :
Subtrair o Zi dos desvios –padrão para encontrar a % de prbabilidade.
P= 0,99379-0,006209665
P= 0,98758 ou seja 98,75% de probabilidade resultando em 9876 mensurações
dentro de 2,5 desvios-padrão
Representando Graficamente
Distribuição norma 2,5 desvios- padrão
98,76%
0,621%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
3. Para a distribuição normal, qual é a probabilidade da mensuração de uma peça ficar
no máximo a distância de 3,5 desvios padrão da média das mensurações? Sua
resposta aproximada é
Resposta: Utilizando Tabela 3.1 – Valores de Zi e a área acumulada, a probabilidade
de Zi ser menor.
Zi
-6
-5,9
-5,8
-5,7
-5,6
-5,5
-5,4
-5,3
-5,2
-5,1
-5
-4,9
-4,8
-4,7
-4,6
-4,5
-4,4
-4,3
-4,2
-4,1
-4
Area
acumulada
a esquerda
0,000000001
0,000000002
0,000000003
0,000000006
0,000000011
0,000000019
0,000000033
0,000000058
0,000000100
0,000000170
0,000000287
0,000000479
0,000000793
0,000001301
0,000002112
0,000003398
0,000005413
0,000008540
0,000013346
0,000020658
0,000031671
Zi
-3,9
-3,8
-3,7
-3,6
-3,5
-3,4
-3,3
-3,2
-3,1
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
-2,0
Area
acumulada
a esquerda
0,000048096
0,000072348
0,000107800
0,000159109
0,000232629
0,000336929
0,000483424
0,000687138
0,000967603
0,001349898
0,001865813
0,002555130
0,003466974
0,004661188
0,006209665
0,008197536
0,010724110
0,013903448
0,017864421
0,022750132
Zi
-1,9
-1,8
-1,7
-1,6
-1,5
-1,4
-1,3
-1,2
-1,1
-1
-0,9
-0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
Area
acumulada
a esquerda
0,02871656
0,035930319
0,044565463
0,054799292
0,066807201
0,080756659
0,096800485
0,11506967
0,135666061
0,158655254
0,184060125
0,211855399
0,241963652
0,274253118
0,308537539
0,344578258
0,382088578
0,420740291
0,460172163
Zi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
Area
acumulada
a esquerda
0,5
0,539827837
0,579259709
0,617911422
0,655421742
0,691462461
0,725746882
0,758036348
0,788144601
0,815939875
0,841344746
0,864333939
0,88493033
0,903199515
0,919243341
0,933192799
0,945200708
0,955434537
0,964069681
0,97128344
Zi
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
Area
acumulada
a esquerda
0,97725
0,982136
0,986097
0,989276
0,991802
0,99379
0,995339
0,996533
0,997445
0,998134
0,99865
0,999032
0,999313
0,999517
0,999663
0,999767
0,999841
0,999892
0,999928
0,999952
Zi
4
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6
Area
acumulada
a esquerda
0,999968329
0,999979342
0,999986654
0,99999146
0,999994587
0,999996602
0,999997888
0,999998699
0,999999207
0,999999521
0,999999713
0,999999830
0,999999900
0,999999942
0,999999967
0,999999981
0,999999989
0,999999994
0,999999997
0,999999998
0,999999999
Para 3,5 desvios – padrão Temos : Zi = 0,999767 e 0,000232629
Para encontrar a probabilidade de uma mensuração ficar no máximo à distância de 3,5
desvios-padrão da média subtraímos os valores Zi encontrados
P= 0,999767-0,000232629
P= 0,99953 ou seja 99,95% de probabilidade
Representando Graficamente:
Distribuição norma 2,5 desvios- padrão
99,95%
0,023%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
4. Para mensurações que seguem a distribuição normal, qual é a probabilidade de uma
mensuração ficar fora dos limites de especificação de três desvios padrão da média?
Sua resposta aproximada em PPM é
Resposta: Deve – se calcular a área total embaixo Curva e subtrair a área das caudas
“α” e transformar para PPM. Neste caso:
PPM = (1 – (0,0135 * 2))*1.000.000
PPM= 2.700
-
5. Para a distribuição normal, qual é a probabilidade de rejeitar uma peça cujo único
limite de especificação é o superior e fica a distância de seis desvios padrão da média?
Sua resposta aproximada é
Reposta : Neste caso a distribuição normal está contida em seis desvios padrão
conforme gráfico abaixo
Distribuição normal em desvio padrão
0,999999998
0,000000001
-7
-6
-5
-4
-3
-2
PPM= 0,000000001*1.000.000.
PPM = 0,001
-1
0
1
2
3
4
5
6
7
6. Um engenheiro rejeita todo produto que está fora dos limites de especificação.
Nesse momento, a linha está produzindo uma taxa de 10% de rejeito simetricamente
acima e abaixo dos limites de especificação. No entanto, ele é descontente com a alta
taxa de rejeição e quer uma taxa ao máximo de 2%. Ele vê duas alternativas: ou
diminuir o desvio padrão do processo ou aumentar os limites de especificação. Qual é
a alternativa mais econômica no curto prazo? Outra questão importante é se o
engenheiro optar para diminuir o desvio padrão do processo, qual é a relação entre o
desvio padrão novo que é menor e o desvio padrão velho que é obviamente maior?
Elaborar sua resposta usando a distribuição normal padronizada.
Resposta. A principio alterar os limites de especificação seria mais fácil, porém nem
sempre é possível dependendo do processo poderá não ser aceito pelo cliente, por
exemplo, com contratos já firmados. Por outro lado reduzir o desvio padrão é muito
custoso para as organizações, porém as vezes é necessário devido as exigências do
mercado e a vantagem da imagem atribuída a organização como por exemplo empresa
de classe mundial.
Se optar por diminuir o desvio padrão tem- se:
Processo atual► Área das caudas α = 10% ou 5% por cauda ( α/2 ).
Processo Futuro► Área das caudas α = 2% ou 1% por cauda ( α/2 ).
Na tabela para Valores de Zi e a área acumulada não encontra – se valores exatos
para á área das caudas. Neste caso deve – se fazer a interpolação dos valores
aproximados.
Processo atual :
Zi = 1,7; P(Zi) = 0,044565
Zi
P(Zi) = 0,05
Zi = 1,6 P(Zi) = 0,054799
Sendo assim temos:
(1,7 − 𝑍𝑖)
(1,7 − 1,6)
=
(0,044565 − 0,05)
(0,044565 − 0,054799)
Processo Futuro :
𝑍𝑖 = 1,64
Sendo assim temos:
(2,4 − 𝑍𝑖)
(2,4 − 2,3)
=
(0,008197 − 0,01)
(0,008197 − 0,010724)
𝑍𝑖 = 2,33
Relação entre os processos
Rel=1,64/2,33 = 0,7
NESTE DEVE MELHORAR O DESVIO PADRÃO DO PROCESSO EM 30 %.
Distribuição norma desvios- padrão DESEJADA
98%
1%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6