1.36. A luminária de 50 lb é suportada por duas hastes de aço

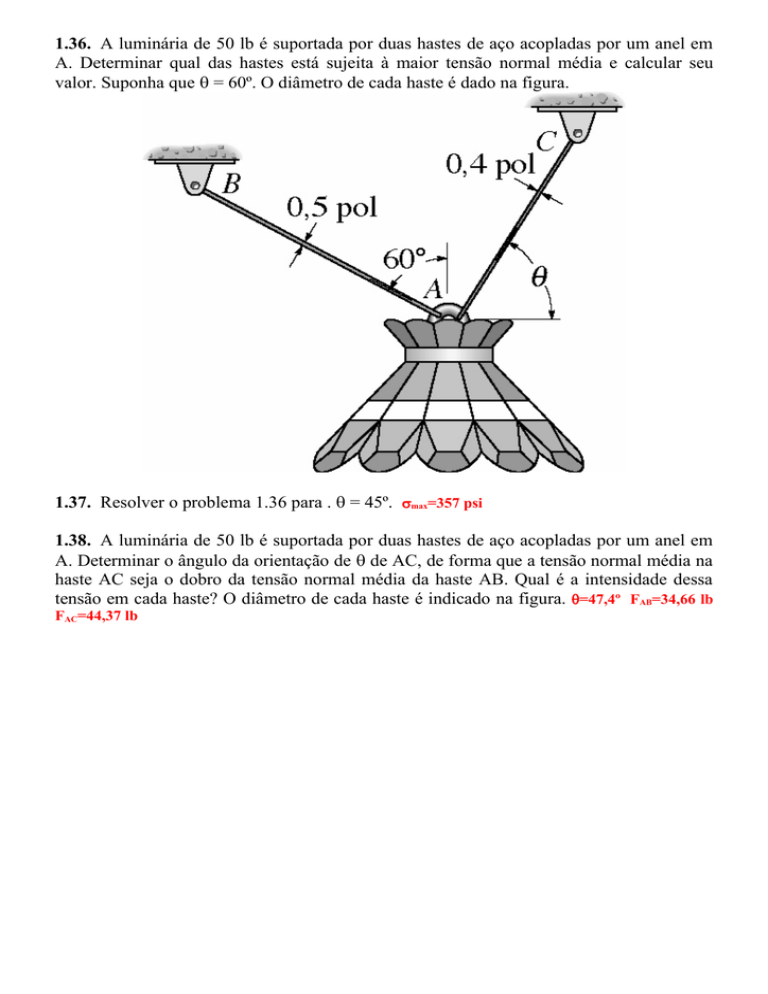
1.36. A luminária de 50 lb é suportada por duas hastes de aço acopladas por um anel em
A. Determinar qual das hastes está sujeita à maior tensão normal média e calcular seu
valor. Suponha que θ = 60º. O diâmetro de cada haste é dado na figura.
1.37. Resolver o problema 1.36 para . θ = 45º. σmax=357 psi
1.38. A luminária de 50 lb é suportada por duas hastes de aço acopladas por um anel em
A. Determinar o ângulo da orientação de θ de AC, de forma que a tensão normal média na
haste AC seja o dobro da tensão normal média da haste AB. Qual é a intensidade dessa
tensão em cada haste? O diâmetro de cada haste é indicado na figura. θ=47,4º FAB=34,66 lb
FAC=44,37 lb
1.43. Os pinos em B e C da estrutura têm, cada um, um diâmetro de 0,25 pol. Supondo
que os pinos estejam submetidos a cisalhamento duplo, determinar a tensão de
cisalhamento média em cada pino. (τB)med = 6053 psi = 6,05 ksi
1.44. Resolver o problema 1.43 supondo que os pinos B e C sejam submetidos a
cisalhamento simples. (τB)med = 12,1 ksi
1.45. Os pinos em D e E da estrutura têm, cada um, um diâmetro de 0,25 pol. Supondo
que os pinos estejam submetidos a cisalhamento duplo, determinar a tensão de
cisalhamento média em cada pino. (τD)med = 6621 psi = 6,62 ksi
1.46. Resolver o problema 1.45 supondo que os pinos D e E sejam submetidos a
cisalhamento simples. (τD)med = 13,2 ksi (τE)med = 12,4 ksi
1.56. A junta está submetida à força de 6 kip do elemento axial. Determinar a tensão
normal média que atua nas seções AB e BC. Supor que o elemento é plano e tem 1,5
polegada de espessura.
1.60. As barras da treliça têm uma área da seção transversal de 1,25 pol2. Determinar a
tensão normal média em cada elemento devido à carga P = 8 kip. Indicar se a tensão é de
tração ou de compressão.
1.61. As barras da treliça têm uma área da seção transversal de 1,25 pol2. Supondo que a
tensão normal média máxima em cada barra não exceda 20 ksi, determinar a grandeza
máxima P das cargas aplicadas à treliça. P = 6,82 kip
1.77. O elemento B está submetido a uma força de compressão de 800 lb. Supondo que A
e B sejam ambos de madeira e tenha 3/8 pol de espessura, determinar, com aproximação
de ¼ pol, a menor dimensão h do apoio de modo que a tensão de cisalhamento média não
exceda τadm = 300 psi. h = 2 ¾ pol
1.79. O olhal é usado para suportar uma carga de 5 kip. Determinar seu diâmetro d, com
aproximação de 1/8 pol, e a espessura h necessária, de modo que a arruela não penetre ou
cisalhe o apoio. A tensão normal admissível do parafuso é σadm = 21 ksi, e a tensão de
cisalhamento admissível do material do apoio é τadm = 5 ksi. d = 5/8 pol h = 3/8 pol
1.80. A junta sobreposta do elemento de madeira A de uma treliça está submetida a uma
força de compressão de 5 kN. Determinar o diâmetro requerido d da haste de aço C e a
altura h do elemento B se a tensão normal admissível do aço é (σadm)aço = 157 MPa e a
tensão normal admissível da madeira é (σadm)mad = 2 MPa. O elemento B tem 50 mm de
espessura.
1.88. Os suportes apóiam a vigota uniformemente; supõe-se então que os quatro pregos
em cada suporte transmitem uma intensidade igual da carga. Supondo que a vigota esteja
submetida ao carregamento mostrado, determinar a tensão de cisalhamento média em cada
prego do suporte nas extremidades A e B. Cada prego tem 0,25 pol de diâmetro. Os
suportes resistem apenas a cargas verticais.
1.89. Os suportes apóiam a vigota uniformemente; supõe-se então que os quatro pregos
em cada suporte transmitem uma intensidade igual da carga. Determinar o menor diâmetro
dos pregos em A e B se a tensão de cisalhamento admissível para os pregos for de τ
dB = 0,162 pol
adm = 4 ksi. Os suportes resistem apenas a cargas verticais. dA = 0,155 pol
1.96. Supondo que a tensão de apoio admissível para o material sob o apoio em A e B seja
(σb)adm = 400 psi, determinar a carga máxima P que pode ser aplicada à viga. As placas de
apoio A’ e B’ têm seção transversal quadrada de 2 pol × 2 pol e 4 pol × 4 pol,
respectivamente.
1.97. Supondo que a tensão de apoio admissível para o material sob o apoio em A e B seja
(σb)adm = 400 psi, determinar o tamanho das placas de apoio quadradas A’ e B’ necessário
para suportar a carga. Dimensionar as placas com aproximação de ½ pol. As reações nos
apoios são verticais. Suponha que P = 1500 lb. placas 3 ½ pol x 3 ½ pol e 4 ½ pol x 4 ½ pol
1.103. O conjunto é usado para suportar a carga distribuída w = 500 lb/pé. Determinar o
fator de segurança em relação ao limite de elasticidade para a haste de aço BC e os pinos
em B e C se o limite de elasticidade do aço na tração é σp = 36 ksi e no cisalhamento τ
p = 18 ksi. A haste tem 0,4 pol de diâmetro e cada pino tem 0,30 pol de diâmetro. F.S.=2,71
e F.S.=1,53
1.104. Supondo que a tensão de cisalhamento admissível para cada um dos pinos de aço
de 0,3 pol de diâmetro em A, B e C seja τadm = 12,5 ksi e a tensão normal admissível para a
haste BC de 0,40 pol de diâmetro seja σadm = 22 ksi, determinar a maior intensidade w da
carga distribuída uniforme que pode ser suportada pela viga.
1.112. As duas hastes de alumínio suportam a carga vertical P = 20 kN. Determinar seus
diâmetros requeridos se o esforço de tração admissível para o alumínio for σ
adm = 150 MPa.