Força em trajetórias curvilíneas

Força em trajetórias curvilíneas
•
•
Em trajetórias curvilíneas há variação da velocidade vetorial.
A força centrípeta aponta para o cento da circunferência e pode ser calculado pela fórmula:
=
•
.
→
²
=
Em uma pista sobrelevada, desprezando a força de atrito, pode-se determinar a seguinte relação:
=
sendo
•
.
Em uma pista plana a velocidade máxima que um carro consegue fazer uma curva sem derrapar é calculada pela
fórmula:
á
•
=
²
o ângulo de sobrelevação.
Exercícios clássicos:
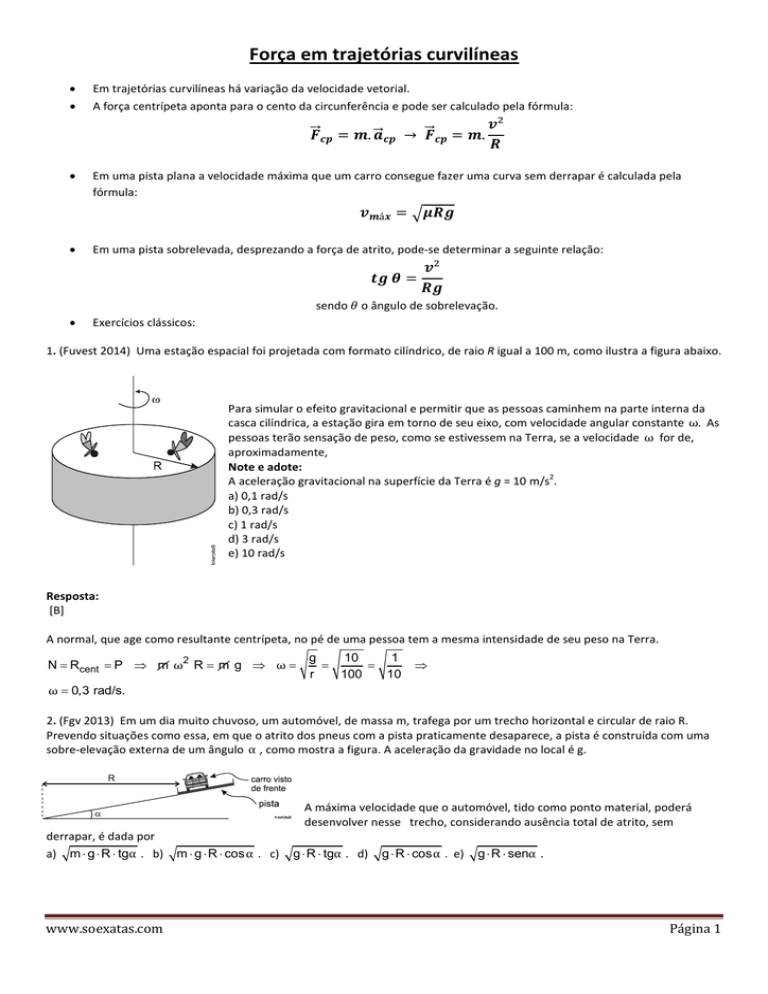
1. (Fuvest 2014) Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como ilustra a figura abaixo.
Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da
casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante ω. As
pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de,
aproximadamente,
Note e adote:
2
A aceleração gravitacional na superfície da Terra é g = 10 m/s .
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
Resposta:
[B]
A normal, que age como resultante centrípeta, no pé de uma pessoa tem a mesma intensidade de seu peso na Terra.
N = Rcent = P ⇒ m ω2 R = m g ⇒ ω =
g
10
1
=
=
r
100
10
⇒
ω = 0,3 rad/s.
2. (Fgv 2013) Em um dia muito chuvoso, um automóvel, de massa m, trafega por um trecho horizontal e circular de raio R.
Prevendo situações como essa, em que o atrito dos pneus com a pista praticamente desaparece, a pista é construída com uma
sobre-elevação externa de um ângulo α , como mostra a figura. A aceleração da gravidade no local é g.
A máxima velocidade que o automóvel, tido como ponto material, poderá
desenvolver nesse trecho, considerando ausência total de atrito, sem
derrapar, é dada por
a) m ⋅ g ⋅ R ⋅ tgα . b)
www.soexatas.com
m ⋅ g ⋅ R ⋅ cosα . c)
g ⋅ R ⋅ tgα . d)
g ⋅ R ⋅ cosα . e)
g ⋅ R ⋅ senα .
Página 1
Resposta:
[C]
A figura 1 mostra as forças (peso e normal) agindo nesse corpo. A resultante dessas forças é a centrípeta (figura 2).
Na figura 2, o triângulo é retângulo:
R
tg α = C =
P
v=
m v2
R
m g
⇒ tg α =
v2
R g
⇒ v 2 = R g tg α ⇒
R g tg α .
3. (Cesgranrio 2011) Uma esfera de massa igual a 3 kg está amarrada a um fio inextensível e de massa desprezível. A esfera gira
com velocidade constante em módulo igual a
4 6
m/s, formando um cone circular imaginário, conforme a figura abaixo.
15
O fio permanece esticado durante todo o movimento, fazendo um mesmo ângulo α com a
vertical, cuja tangente é 8/15. A componente horizontal da tração no fio vale 16 N e é a força
3
centrípeta responsável pelo giro da esfera. O volume do cone imaginário, em cm , é
a) 280π
b) 320π
c) 600π
d) 960π
e) 1800π
Resposta:
[B]
2
4 6


2
2
mV / R V
8  15 
8
96
96x15
tgα =
=
→
=
→
= 2
→R =
= 0,08m = 8cm
mg
Rg
15
10R
15 15 x10R
80x15 2
tgα =
V=
R
8 8
→
= → h = 15cm
h
15 h
1
1
πR 2h = π.82.15 = 320 π cm3
3
3
4. (Ufsc 2010) Rotor é um brinquedo que pode ser visto em parques de diversões.Consiste em um grande cilindro de raio R que
pode girar em torno de seu eixo vertical central. Após a entrada das pessoas no rotor, elas se encostam nas suas paredes e este
começa a girar. O rotor aumenta sua velocidade de rotação até que as pessoas atinjam uma velocidade v, quando, então, o piso
www.soexatas.com
Página 2
é retirado. As pessoas ficam suspensas, como se estivessem “ligadas” à parede interna do cilindro enquanto o mesmo está
girando, sem nenhum apoio debaixo dos pés e vendo um buraco abaixo delas.
Em relação à situação descrita, é CORRETO afirmar que:
01) a força normal, ou seja, a força que a parede faz sobre uma pessoa encostada na parede do
rotor em movimento, é uma força centrípeta.
02) se duas pessoas dentro do rotor tiverem massas diferentes, aquela que tiver maior massa
será a que terá maior chance de deslizar e cair no buraco abaixo de seus pés.
04) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa
gR
dentro dele deve ser maior ou igual a
.
ν2
08) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa
dentro dele é proporcional ao raio do rotor.
16) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa
dentro dele é proporcional à velocidade v do rotor.
Resposta:
01 + 04 = 05
A figura a seguir mostra as forças que agem na pessoa.
01) Correta . A força normal ( N ) é sempre perpendicular a superfície de apoio, conforme ilustra
a figura acima. Nesse caso ela é dirigida para o centro, portanto é uma força centrípeta.
02) Falsa. Como a pessoa efetua movimento circular uniforme, na direção horizontal a normal age
como resultante centrípeta ( R Cent ) e, na direção vertical, a força de atrito ( Fat ) deve equilibrar o
peso. O piso somente deve ser retirado quando a força de atrito estática máxima for maior ou igual
ao peso, caso contrário a pessoa escorrega pelas paredes. Assim:
mv 2
N=
R
Fat ≥ P ⇒ µ N ≥ m g. Inserindo nessa expressão a expressão anterior, vem:
µ m v2
R g
R g
≥ m g ⇒ µ≥
⇒ v≥
. Nessa expressão, vemos que a massa da pessoa não interfere e que a
2
R
µ
v
velocidade mínima com que o piso pode ser retirado depende apenas do raio do rotor da intensidade do campo
gravitacional local e do coeficiente de atrito entre as roupas da pessoa e a parede do rotor.
04) Verdadeira, conforme demonstração no item anterior.
08) Falsa. O coeficiente de atrito depende apenas das características das superfícies em contato.
16) Falsa, conforme justificativa do item anterior.
5. (Ita 2009)
°
A partir do repouso, um carrinho de montanha russa desliza de uma altura H = 20 3 m sobre uma rampa de 60 de inclinação e
corre 20 m num trecho horizontal antes de chegar a um loop circular, de pista sem atrito.
1
, assinale o valor do
2
raio máximo que pode ter esse loop para que o carrinho faça todo o percurso sem perder o
contato com a sua pista.
Sabendo que o coeficiente de atrito da rampa e do plano horizontal é
www.soexatas.com
Página 3
a) R = 8 3 m b) R = 4( 3 - 1)m c) R = 8( 3 - 1)m d) R = 4(2 3 -1)m e) R = 40
(
)m
3 −1
3
Resposta:
[B]
2
No ponto máximo do looping para que o corpo complete o percurso P = m.g = m.v /R
O comprimento da rampa
→ v2 = R.g
→ cos60° = H/L → L = 40 m
A energia gravitacional no início da rampa
→ Eg = m.g.H = 20mg 3
→ W = F.d = µNL = µmgL = 10mg 3
O trabalho do atrito no deslocamento horizontal → W’ = µNd = 10mg
A energia cinética do início do looping → Ec = Eg - W - W’
O trabalho do atrito na rampa
Ec = 20 mg
3 – 10 mg 3 – 10 mg = 10 mg( 3 – 1)
Esta energia cinética se converte em gravitacional e cinética no alto do looping
10 mg(
3 – 1) = mg.2R + (m/2).Rg
10(
3 – 1) = 2R + R/2
10(
3 – 1) = 5R/2
R = 4.(
3 – 1) m
•
Resultante centrípeta e resultante tangencial
No movimento circular uniforme a resultante das forças é a força centrípeta.
Nos movimentos curvilíneos variados, tem-se tanto a força centrípeta quanto a força tangencial.
•
Força em referencial não-inercial
A força centrífuga só existe para referenciais não-inerciais. Assim, um motorista ao fazer uma curva sente uma
força que apresenta sentido do centro para fora da curva.
Bibliografia:
Junior, Francisco R.; Ferraro, Nicolau G. ; Soares, Paulo A. de Toledo. Fundamentos da física 1. 9ª Edição. São Paulo, moderna, 2007.
www.soexatas.com
Página 4