MOVIMENTO RELATIVO

1
MOVIMENTO RELATIVO
• O movimento é um conceito relativo cuja descrição depende de
um referencial específico escolhido pelo observador.
• Diferentes observadores usando sistemas referenciais diferentes
obtém diferentes descrições de um mesmo movimento.
• Como relacionar estes resultados distintos de um mesmo
movimento ?
• É esse o objectivo do estudo do movimento relativo.
• Um referencial é escolhido de modo a facilitar a descrição do
movimento do objecto que se pretende estudar. Exemplos:
• movimentos na Terra : referenciais ligados à Terra
• astronomia : referenciais em estrelas que se podem
considerar imóveis (“estrelas fixas”)
• física atómica : referencial no núcleo atómico (os electrões
são muito mais leves que o núcleo podendo-se considerar
que a posição nuclear é fixa relativamente aos electrões)
• Não existe um referencial absoluto.
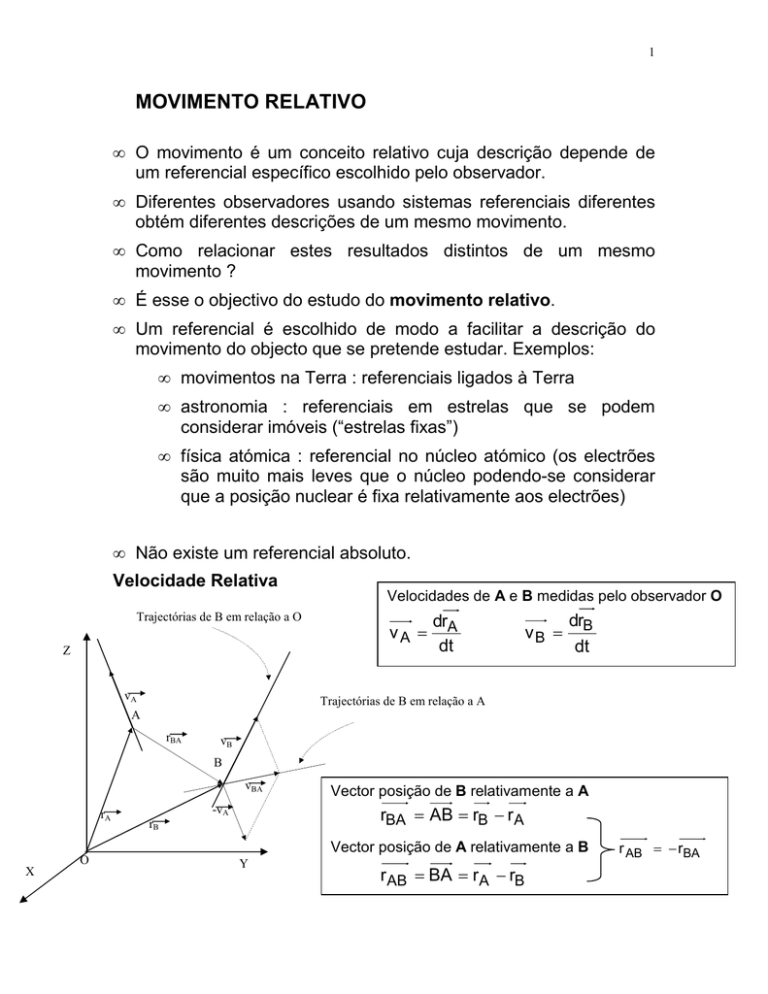
Velocidade Relativa
Trajectórias de B em relação a O
Z
vA
Velocidades de A e B medidas pelo observador O
vA =
drA
dt
vB =
drB
dt
Trajectórias de B em relação a A
A
rBA
vB
B
vBA
rA
Vector posição de B relativamente a A
rBA = AB = rB − r A
-vA
rB
Vector posição de A relativamente a B
O
X
Y
r AB = BA = rA − rB
r AB = − rBA
2
Velocidade de B em relação a A: v BA =
Velocidade de A em relação a B:
v AB =
drBA
dt
v BA = −v AB
drAB
dt
drBA drB drA
=
−
⇔ v BA = v BO − v A O = v B − v A
dt
dt
dt
Velocidades de B e A relativas a O
(por vezes omite-se o índice O)
drAB drA drB
=
−
⇔ v AB = v A O − v B O = v A − v B
dt
dt
dt
Aceleração Relativa
Aceleração de B em relação a A: a BA =
dv BA
dt
a BA = −a AB
dv AB
Aceleração de A em relação a B: a
AB =
dt
dv BA dv B dv A
=
−
⇔ a BA = a B − a A
dt
dt
dt
aA e aB são as
Acelerações de B e A
relativas a O
dv AB dv A dv B
=
−
⇔ a AB = a A − a B
dt
dt
dt
3
Exemplo:
Considere dois aviões A e B deslocam-se, num dado instante,
com as velocidades indicadas na figura seguinte.
Y
vA = 300kmh
vB = 400kmh
-1
60º
30º
A
-1
B
X
Calcule a velocidade do avião B relativamente ao A e a velocidade
do avião A relativamente ao B.
v A = 300 cos(30 ) i + 300 sen(30 ) j = 259.8 i + 150 j
^
^
^
^
v B = −400 cos(60 ) i + 400 sen(60 ) j = − 200 i + 346.4 j
^
^
^
^
v BA = v B − v A = −459.8 i + 196.4 j v BA = 459.8 2 + 196.4 2 = 500kmh −1
Cos(θ X ) = −459.8 / 500 ⇒ θ X = ±157 º
^
^
^
^
v AB = − v BA = 459.8 i − 196.4 j
v AB = 459.8 2 + 196.4 2 = 500kmh −1
Cos(θ X ) = +459.8 / 500 ⇒ θ X = ±23º
Y
vB
vA
vBA
60º
157º
30º
A
X
-23º
vAB
-vB
-vA
B
4
Movimento Relativo De Translacção
Seja O´x´y´z´ um referêncial móvel com velocidade vTr em relação ao
referencial fixo Oxyz
v ≡ v A / O é a velocidade absoluta = v obj./ref.fixo
v´ ≡ v A / O´ é a velocidade relativa = v obj./ref.m óvel
v Tr ≡ v O´/ O é a velocidade de transporte = v ref.móvel/ ref.fixo
tem-se
v = v´ + v Tr ⇔ v obj. / ref .fixo = v obj. / ref .móvel + v ref .móvel / ref .fixo
ou
v´ = v − v Tr ⇔ v obj. / ref .móvel = v obj. / ref .fixo − v ref .móvel / ref .fixo
• Acelerações
a = a´ + a Tr ⇔ aobj. / ref .fixo = aobj. / ref .móvel + aref .móvel / ref .fixo
ou
a´ = a − a Tr ⇔ aobj. / ref .móvel = aobj. / ref .fixo − aref .móvel / ref .fixo
Se a velocidade de transporte fôr constante aTr = 0 e logo
A aceleração é invariante em todos os referenciais animados de
movimento relativo de translacção uniforme
Referenciais inerciais
5
• Componentes normal e tangencial da aceleração
como a aceleração está dirigida para a concavidade da
trajectória pode-se decompô-la em duas componentes, uma
tangencial (aT) e outra normal (aN) à trajectória
aT
a
aN
aT descreve a variação do módulo da velocidade
aN descreve a variação da direcção da velocidade
Considerando o versor da tangente à trajectória (ûT) tem-se:
a =
(
)
d vûT
dû T
dv
dv
=
=
ûT + v
dt
dt
dt
dt
Variação do módulo da
velocidade
Variação da direcção
da velocidade
dû T
Qual o valor de
dt
?
C
dφ
^
dφ
ρ
A’
ds
ûN
φ
^j
^i
ds é o arco entre A e A´
A
û
φ T
v
û T = cos(φ) i + sen(φ) j
^
^
ûN
π
π^


= cos φ +  i + sen φ +  j
2
2


^
= − sen(φ) i + cos (φ) j
^
6
dû T
dt
dû T
dt
=
d 
dφ ^
dφ ^
^
^
cos(φ) i + sen(φ) j  = −sen(φ)
i + cos(φ)
j

dt 
dt
dt

=
dφ
û
dt N
conclui-se que
dû T
dt
é normal à trajectória
introduzindo o deslocamento na trajectória, ds, obtém-se
dφ dφ ds
dφ
=
=v
dt ds dt
ds
As normais às curvas nos pontos A e A´ interseptam-se no ponto C
que se designa por centro de curvatura. Este ponto permite definir
o raio de curvatura, ρ, como a distância entre os pontos C e A.
ds pode ser calculado por ds = ρ dφ
logo
dφ 1
=
ds ρ
conclui-se então que
dû T
dt
=
v
û
ρ N
dv
v2
a =
û +
û
dt T
ρ N
aT
a=
2
a 2T + a N
aN
2
v4
 dv 
=   +
 dt 
ρ2
7
Movimento Circular
Trajectória deste movimento é uma circunferência
v
A
R
θ
θ=
s
C
X
s
⇔ s = Rθ
R
(θ em radianos )
A velocidade é perpendicular ao raio R=CA pois a
velocidade é tangente à circunferência
v=
ds
dθ
=R
= ωR
dt
dt
Velocidade
-1
escalar (ms )
ω=
dθ
dt
Velocidade
-1
angular (rad s )
Z
R = r sen(γ )
ω
v=ωxr
C R
γ
A
r


dθ ^

ω =
k

dt

v = ω R = ω r sen(γ )

O
Y
X
Só em movimento
circular
(R e γ constantes)
v =ω xr
8
ω
é perpendicular ao plano em que a rotação ocorre
O sentido de ω é determinado pelo sentido do movimento de
rotação através da regra da mão direita ou do saca-rôlhas
• Movimento Circular Uniforme
(ω=constante)
θ
t
dθ
ω=
⇔ dθ = ω dt ⇔ ω ∫ dθ = ∫ dt ⇔ θ = θ o + ω(t − t o )
dt
θ
t
o
o
Neste caso tem-se um movimento periódico pois após uma
rotação de 2π volta-se ao ângulo inicial θo.
Tempo que demora a efectuar uma volta (ou revolução) completa
t
Período : T = n (s)
n
tempo que demora a efectuar n voltas
Número de voltas por unidade de tempo
n
1
Frequênca : f =
=
(s −1 = Hz)
tn T
Se θo=0 e to=0 tem-se θ=ω t <=> ω =
θ
t
logo ω =
2π
= 2π f
T
9
• Aceleração angular
α =
dω
dt
Variação da velocidade
angular com o tempo
No movimento circular a direcção de ω não varia
α=
dω d2 θ
=
dt
dt 2
Quando α é constante obtém-se o
movimento circular uniformemente variado
t
t
to
to
ω = ω o + ∫ α dt = ωo + α ∫ dt = ωo + α (t-t o )
t
t
to
to
θ = θ o + ∫ ω dt = θ o + ∫ [ω o + α ( t − t o )] dt = θ o + ω o (t-t o ) +
α
( t − t o )2
2
• Componentes normal e tangencial da aceleração no movimento
circular
v
C
a = a T + aN
aT = αR ûT
a
aN = ω R ûN
R
θ
2
X
dv
v2
=
ûT +
ûN
dt
R
(
d(ωR )
ωR ) 2
=
ûT +
ûN
dt
R
= αR û T + ω 2R û N