Mecânica Clássica Folha de problemas 5: Dinâmica de fluidos

Mecânica Clássica
(Licenciaturas em Física Ed., Química Ed.)
Folha de problemas 5: Dinâmica de fluidos
1. Durante uma transfusão de sangue, insere-se uma agulha numa veia onde a pressão é 2 kPa
acima da pressão atmosférica. A que altura acima da veia se deve colocar a bolsa de sangue?
Nota: ρsangue =1,05g/cm3 , P0 =1,01×105 N/m2
R: h= 19 cm.
2. Um objecto flutua em água (ρáguae=1,0g/cm3 ), estando 80% do seu volume submerso. Ao
ser colocado num outro líquido, o objecto flutua também, estando agora 72% do seu
volume submerso. Determine:
a) A densidade do objecto; R: ρobj=0,8×103 kg/m3
b) A densidade do líquido. R: ρliq =1,1×103 kg/m3
3. Considere um cubo de 0,6 m de aresta e massa igual a 450 kg suspenso por um fio e
submerso num tanque aberto com um líquido de densidade ρ=1,03×103 kgm-3 . A face
superior do cubo está à profundidade de 0,6 m.
a) Calcule a força total exercida sobre a face superior do cubo. R: 3,86×104 N
b) Calcule a força total exercida sobre a face inferior do cubo. R: 4,08×104 N
c) Obtenha a impulsão exercida pela água sobre o objecto, utilizando o princípio de
Arquimedes. Como se relaciona a impulsão com as forças calculadas nas alíneas anteriores?
R: I=2225 N
d) Calcule a tensão na corda. R: T=2275 N
4. Um anel é formado por uma liga de ouro e prata. O anel pesa 1,96 N no ar e 1,85 N quando
imerso em água. Sabendo que as densidades do ouro e prata são iguais a 19,3×103 kg/m3 e
10,5×103 kg/m3 , respectivamente, determinar a quantidade de ouro e prata presentes no anel.
R: mA g=8,95×10-3 kg; mAu=0,176 kg
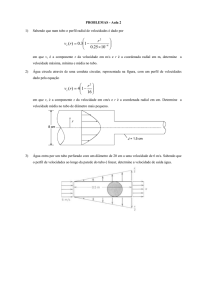
5. Considere um fluido incompressível e não viscoso (i.e. um fluido ideal) que circula no tubo
representado na Figura 1, em
regime estacionário. Os raios do
tubo
em
A
e
B
são,
Β
Α
respectivamente, rA= 5 cm e rB = 1
cm. A velocidade em A é vA = l m/s
e a pressão é PA = 4 atm, e o fluido tem densidade ρ = 1 g/cm3 .
a) Determine a velocidade do fluido em B. R: 25 ms-1 ;
Fig. 1
b) Determine a pressão em B. R: 8,8×04 Pa
c) Mostre que a diferença de pressão ∆ p = pA – pB depende do quociente dos respectivos
raios elevado à quarta potência.
4

1 2  rA 



R: ∆p = ρv A   − 1
2
 rB 

6. As duas asas de um avião têm um perfil tal que, em determinadas condições de vôo, o ar na
parte superior da asa tem uma velocidade de 70 m/s e na parte inferior tem uma velocidade de
60 m/s. Se a massa do avião for igual a 1340 kg e a área de cada asa igual a 16,2 m2 , qual a
resultante da forças verticais aplicadas no avião nestas condições? Nota: ρar=1,29 kgm-3
R: 13767 N
7. O tubo horizontal da Figura 2 tem uma área
de secção recta igual a 40 cm2 na porção mais
larga e de 10 cm2 na porção mais estreita. A
água flui no tubo a uma velocidade
h
10 cm
40 cm
volumétrica de 6 l/s.
a) Obtenha a velocidade da água na secção
mais larga e na mais estreita. R: 6 ms-1
b) a diferença de pressão entre as duas
Fig. 2
porções; R: 1,68 ×104 Pa
c) a diferença de altura entre as colunas de mercúrio no tubo em U. R: 0,12 m
2
2
8. Considere o tanque com água até uma altura de 10 m
a partir do solo, representado na Figura 3. A água
nele contida flui a uma taxa constante através do
tubo, como indicado. O diâmetro do tubo no ponto 2
é igual a 25 cm e no ponto 3 é igual a 15 cm, estando
estes pontos a uma altura de 2 m do solo. Considere
que a secção recta do tanque é muito maior do que
qualquer das secções do tubo e despreze a
viscosidade da água.
a) Determine o caudal volumétrico que sai do tanque
b) Obtenha a pressão no ponto 2.
c) Obtenha o alcance do jacto de água relativamente ao ponto 3.
R: a) qv=0,22 m3 /s; b) P2 =1,69×105 Pa; c) x= 8 m.
9. O tubo da figura 4 tem um diâmetro de 16 cm na
secção 1 e de 10 cm na secção 2, estando em 2 aberto à
atmosfera. No tubo flui água a uma taxa de 0,03 m3 /s.
Desprezando os efeitos da viscosidade, qual o valor da
pressão em 1?
ρágua =1×103 kg/m3
P0 =1×105 Pa
Fig. 4
5
R: P1 =1,66×10 Pa.
40 cm2
Fig. 3
v2
2
6m
v1
1
10. Um aneurisma é um alargamento anormal de um vaso sanguíneo (por exemplo a artéria
aorta). Considere que o sangue se comporta como um fluido não viscoso, em regime
estacionário e que a velocidade do sangue através de uma porção normal da aorta é 0,4 m/s.
Suponha que, devido a um aneurisma, o raio da aorta aumentou 30%.
a) Qual a velocidade do sangue na zona afectada da aorta?
b) Determine a diferença de pressão entre a porção normal e a porção alargada.
Nota: A densidade do sangue é 1,05 g/cm3 .
R: a) 0,226 ms -1 ; b) 57 Pa.
11 – Considere o tanque da figura, aberto e de grandes dimensões, que contém um líquido de
A
densidade ρ. Inicialmente, o
ponto C tem uma tampa na
extremidade, verificando-se que é 6 m
necessário exercer uma força
mínima de 40 N para que esta não
salte. As secções do tubo em B e
6m
em C são iguais a 5 cm2 e 2 cm2 .
B
C
F
a) Considerando desprezável o
atrito entre a tampa e as paredes do tubo, determine a densidade do líquido.
R: ρ=1,67×103 kg/m3
b) Considere agora que a tampa é retirada, passando o líquido a fluir ao longo do tubo. Calcule
a quantidade de líquido que sai pela extremidade do tubo na 1ª hora. R: 11,16 m3
c) Determine a pressão no ponto B. R: 2,67×105 Pa
12 – Considere o conjunto da figura onde o bloco A está
suspenso por uma corda fixa num dinamómetro, D, e submerso
num
líquido C, contido num copo B. A massa do copo é igual a 1 kg e
a
massa do líquido é igual a 1,8 kg. O volume do bloco A é igual a
3,8×10-3 m3 . O conjunto encontra-se no interior de um elevador,
que
se desloca com velocidade constante no sentido descendente.
Nesta
situação a leitura no dinamómetro D indica 35 N e a leitura na
balança E é igual a 7,5 kg.
a) Marque as forças que actuam no bloco A, e para cada uma
delas
indique onde estão aplicados os respectivos pares acção-reacção.
b) Obtenha a densidade do líquido. R: 1,24×103 kg/ m3
c) Determine a massa do bloco A. R: 8,2 kg
d) Suponha que em determinado instante o elevador inicia o processo de travagem, com uma
aceleração constante igual a 3ms-2 . Qual a leitura no dinamómetro D nesta situação? R: 59,6 N
13- Dois tanques abertos, A e F de
grandes dimensões contém água (ver
figura). A altura da água no tanque A é
2 m.
O tubo horizontal BCD sai do fundo do
tanque A, tem um estreitamento em C e
é
aberto em D. A área de secção recta em
C é
10 cm2 e em D é igual a 20 cm2 . Um
tubo
vertical E está ligado ao ponto C e
mergulha no tanque F. Considere a água
incompressível e não viscosa e o fluxo
em
regime estacionário.
a) Qual a quantidade de água que sai no ponto D por unidade de tempo? R: 0,012 m3 /s
b) Qual a pressão no ponto C? R: 4×104 Pa
c) Obtenha a altura h2 a que sobe a água no tubo E. R: 6m
Nota: ρágua = 1,0×103 kg/m3 ; Patm =1,0×105 Pa.