FÍSICA

FÍSICA
5)
CADERNO 4 – CURSO D/E
1) F = 50V2
a)
2
V1 = 2,0m/s
FRENTE 1 – MECÂNICA
n Módulo 15 – Peso de um Corpo
e 3.a Lei De Newton
1)
2)
2) PFD:
01. Falsa. Após ser lançada para cima, a força resultante sobre
a laranja (soma vetorial do peso com a resistência do ar) é
dirigida para baixo.
02. Falsa. No ponto de altura máxima, a velocidade se anula e
a força resultante na laranja é o seu peso.
04. Verdadeira.
08. Falsa. A força dirigida para cima só existe enquanto a laranja está na mão da pessoa, isto é, no ato de lançamento.
16. Verdadeira. É a aceleração da gravidade.
Resposta: 20
a1 = 7,5m/s2
b) V = Vlim, quando F = P
2
2
50Vlim
= 800 ⇒ Vlim
= 16 ⇒ Vlim = 4,0m/s
Respostas: a) 2,0m/s e 7,5m/s2
b) 4,0m/s
6)
a) (F) Para ter o mesmo peso, no mesmo planeta, os corpos
deveriam ter massas iguais.
b) (F) A massa do corpo não depende do local e o corpo A
terá massa de 1,0kg em qualquer planeta.
c) (F) A massa é constante.
d) (F) O peso depende do local.
e) (V) PB = mB gM = 2,5 . 4,0 (N) = 10,0N
PA = mA gT = 1,0 . 10,0 (N) = 10,0N
Resposta: E
a) PFD (objeto):
2F – P = ma
7)
a
P
2F = P + ––– a = P 1 + –– = P
g
g
P – F = ma
800 – 200 = 80a1
Desprezando-se o efeito do ar, a única força atuante na bola
é o seu peso, que tem direção vertical, sentido para baixo e
módulo P = mg = 6,5N.
3)
2
200 = 50V1 ⇒ V1 = 4,0
–––––
g
g+a
a) Morango em equilíbrio:
→ →
F =0
→ → →
F + P = 0
→
direção de F : vertical
→
→
→
F =– P ⇒
sentido de F = para cima
→
→
F = P
P
g+a
F = ––– –––––––
2
g
→
b) Reação à força F : na saladeira
Reação ao peso: na Terra
b) Para o equilíbrio:
2F = P ⇒
8)
P
F = –––
2
P
Respostas: a) F = –––
2
–––––
g
g+a
P
b) F = –––
2
4)
a) Como a força tensora T = 1200N é maior que o peso do
bloco P = 1000N, a aceleração →
a é dirigida para cima.
I. Falsa.
O corpo pode estar em MRU.
II. Falsa.
→
→
N e P não são, entre si, ação e reação, pois estão
aplicadas ao mesmo corpo.
III. Correta.
A reação tem a mesma intensidade da ação (peso).
IV. Falsa.
Ação e reação têm sempre a mesma intensidade.
Resposta: B
9)
PFD: T – P = m a
1200 – 1000 = 100 . a ⇒
a = 2,0m/s2
b) O sentido do movimento (subindo ou descendo) não está
determinado.
O helicóptero pode estar subindo com movimento ace→
→
lerado (↑ V ↑ a ) ou descendo com movimento retardado
→ →
(↓ V ↑ a ).
–1
2) PFD (A):
A força resultante é nula:
T = mAa
2T=P
T = 1,0 . 2,0 (N) ⇒
P
600
T = –– = –––– (N)
2
2
T = 2,0N
Resposta: A
3)
T = 300N
a)
Resposta: 300N
10) a) A força que a Terra aplica sobre a esfera é o seu peso:
FTE = PE = mEg = 24 . 10 (N) = 240N
De acordo com a 3.a Lei de Newton (ação e reação), a
esfera aplica sobre a Terra uma força de mesma
intensidade: 240N.
b) Aplicando-se a 2.a Lei de Newton à Terra, vem:
1) O dinamômetro ideal tem massa desprezível; a força
resultante sobre ele é sempre nula e a força que ele
indica é a força aplicada em uma de suas
extremidades.
2) PFD (B): T = mB a
20,0 = 5,0 . a ⇒ a = 4,0m/s2
FET = mT aT
240 = 6,0 . 1024 aT ⇒ aT = 4,0 . 10–23m/s2
10–23
< 4,0 .
10–23
<
b) PFD (A + B):
10–22
Como 4,0 > 10 , a ordem de grandeza é
F = (mA + mB) a
10–22m/s2
F = 11,0 . 4,0 (N) ⇒
Respostas: a) 2,4 . 102N
b) 10–22m/s2
F = 44,0N
Respostas: a) 4,0m/s2
b) 44,0N
11) (1) Correta.
PFD: F – P = ma
4)
a) PFD (A + B + C):
F = (mA + mB + mC) a
F = m (a + g)
30,0 = 12,0 a ⇒
a = 2,5m/s2
F = 1,0 (12,0) (N)
b) PFD (B + C):
F = 12,0N
FAB = (mB + mC) a
FAB = 8,0 . 2,5 (N) ⇒
(2) Correta. P = mg = 10,0N
→
(3) Correta. É a reação à força F .
(4) Falsa.
Resposta: B
FAB= 20,0N
c) PFD (C):
FBC = mC a
FBC = 2,0 . 2,5 (N)
n Módulo 16 – Aplicações
das Leis de Newton
FBC = 5,0N = FCB (ação e reação)
Respostas: a) 2,5m/s2
b) 20,0N
1)
1) PFD (A + B):
F = (mA + mB) a
c) 5,0N
7,0 = 14,0 . a
a = 0,5m/s2
2) PFD (B):
FAB = mB a
FAB = 6,0 . 0,5 (N)
5)
a) PFD (A + B + C):
F = (mA + mB + mC) a
30 . 103 = 60 . 103 . a
a = 0,5m/s2
FAB = 3,0N
3) Lei da ação e reação:
FBA = FAB = 3,0N
b) PFD (B + C):
FAB = (mB + mC) a
FAB = 30 . 103 . 0,5 (N)
Resposta: B
FAB = 15kN
2)
1) PFD (A + B):
F = (mA + mB) a
6,0 = 3,0a ⇒
2–
a = 2,0m/s2
c) PFD (C):
FBC = mC a
FBC = 25 . 103 . 0,5 (N)
FBC = 1,25 . 104 N
b) Isolando-se o bloco superior (A), vem:
2.a Lei de Newton no bloco A:
FBC = 12,5kN
Fat
= mA a
Fat
= 2,0 . 0,40 (N)
BA
Respostas: a)
0,5m/s2
b) 15kN
BA
c) 12,5kN
Fat
BA
6)
a) PFD (A + B + C):
F1 – F2 = (mA + mB + mC) a
= 0,80N
Respostas: a) A aceleração tem módulo 0,40m/s2
b) 0,80N
b) PFD (A):
9)
1) PFD (A + B + corda): F = (mA + mB + mC) a
36,0 – FBA = 4,0 . 3,0
FBA = 24,0 N
AB
(ação e reação)
36,0 – 12,0 = 8,0a ⇒ a = 3,0 m/s2
F1 – FBA = mA . a
= Fat
12,0 = 6,0 . a ⇒
a = 2,0m/s2
2) PFD (B + metade da corda):
FAB = FBA = 24,0 N
c) PFD (C):
FBC – F2 = mC . a
FBC – 12,0 = 2,0 . 3,0
FBC = 18,0 N = FCB
mC
T = mB + –––
2
a
T = (2,0 + 0,5) . 2,0 (N)
T = 5,0N
Para conferir:
FAB – FCB = mB . a
Resposta: C
24,0 – 18,0 = 2,0 . a
10) 1) PFD (A + B):
a = 3,0 m/s2
F1 – F2 = 3Ma
29,0 – 5,0 = 3Ma
Ma = 8,0
Respostas: a) 3,0 m/s2
b) FAB = FBA = 24,0 N
2) PFD (B):
c) FBC = FCB = 18,0 N
FH – F2 = 2Ma
7)
1) PFD (A + B + C):
F = (mA + mB + mC) a
2) PFD (B + C):
T1 = (mB + mC) a
3) PFD (C):
T2 = mC a
FH – 5,0 = 16,0
FH = 21,0 N
3) PFD (A):
F = T1 + T2 ⇒
(mA + mB + mC) a = (mB + mC + mC) a
mA + mB + mC = mB + 2 mC
F1 – FH = Ma
29,0 – FH = 8,0
FH = 21,0N
mC = mA
(mB qualquer)
Resposta: C
8)
a) Aplicando-se a 2.a Lei de Newton ao conjunto dos dois
blocos, vem:
F = (mA + mB) a
2,0 = 5,0 . a
a = 0,40m/s2
A haste está sendo tracionada por uma força de intensidade FH = 21,0N.
A força resultante na haste é nula porque ela tem massa
desprezível.
Resposta: C
–3
n Módulo 17 – Aplicações
das Leis de Newton
d) Em (1):
1)
e) Se invertermos A e B:
a) PFD (A + B):
F – (PA + PB) = (mA + mB) a
F – 60,0 = 6,0 . 2,0
M
Mg
a2
a2 = ––––––––– e –––– = –––––
m+M
a1
m
F = 72,0N
b)
M
a2 = –––– a1
m
PFD (B): T – PB = mB a
T – 40,0 = 4,0 . 2,0
mMg
T2 = ––––––––– ⇒
m+M
T = 48,0N
Respostas: a) 72,0N
2)
M mg
T1 = ––––––––
M+m
4)
b) 48,0N
T2 = T1
a) 1) A partir do gráfico:
V
1,0
a = –––– = –––– (m/s2) = 0,5m/s2
t
2,0
a) Considere o sistema constituído pelos três elos e m = massa de cada elo.
PFD (sistema):
2) PFD (m1): T = m1 a
(1)
F–3mg=3ma
PFD (m2): m2g – T = m2a
(2)
F = 3 m (a + g)
PFD (m1 + m2): m2g = (m1 + m2) a
F = 3 . 0,10 . 13 (N)
10,0 = (m1 + 1,0) 0,5
20,0 = m1 + 1,0 ⇒ m1 = 19,0kg
F = 3,9N
b)
m2g – FN = m2a (3)
b) PFD (elo): FR = m a
FR = 0,10 . 3,0 (N)
Comparando-se (2) e (3):
FR = 0,30N
c)
FN = T = 19,0 . 0,5 (N) ⇒ FN = 9,5N
PFD (elo de baixo):
F1 – m . g = m . a ⇒ F1 = m . a + m . g
F1 = m . (a + g) = 0,10 . 13 (N)
F1 = 1,3N
Respostas: a) 3,9N
Respostas: a) 19,0kg
b) 0,30N
c) 1,3N
5)
3)
b) 9,5N
a) PFD (A + B + C):
PC = (mA + mB + mC) a
a)
50,0 = (3,0 + 2,0 + 5,0) a
a = 5,0 m/s2
b) PFD (B):
FAB = mB a
FAB = 2,0 . 5,0 (N)
b) Como não há atrito, não há resistência ao movimento e
quaisquer que sejam as massas M e m o sistema sempre
será acelerado.
c) PFD (A): T1 = Ma1
c) PFD (A + B):
(1)
PFD (B): PB – T1 = ma1
(2)
PFD (A + B): (1) + (2) PB = (M + m) a1
mg
mg = (M + m) a1 ⇒ a1 = ––––––––
M+m
4–
FAB = 10,0 N
T = (mA + mB) a
T = 5,0 . 5,0 (N) ⇒
Respostas: a) 5,0m/s2
T = 25,0 N
b) 10,0N
c) 25,0N
6)
a) PFD (A + B + C):
PA = (mA + mB + mC) a
8)
a) Para que o bloco A não se movimente verticalmente, temos:
40,0 = 8,0 a ⇒ a = 5,0m/s2
b) PFD (B + C):
T = PA = mA g = 0,3 . 10(N) ⇒ T = 3,0N
T = (mB + mC) a
b) A força aplicada pelo fio é a resultante que acelera o bloco
T = 4,0 . 5,0 (N) ⇒ T = 20,0 N
B:
c)
PFD (C): Fat
BC
Fat
BC
Fat
= mC . a
PFD (B): T = mB a
= 1,0 . 5,0 (N)
m A g = mB a
BC
= 5,0N = Fat
mA
0,3
a = ––––
g = –––– . 10 (m/s2)
0,2
mB
CB
a = 15m/s2
Respostas: a) a = 5,0m/s2
b) T = 20,0N
c) Fat = 5,0N
→
c) A força F é a resultante que acelera todo o sistema
(A + B + C):
PFD (A + B + C):
7)
a) Quando o eixo da polia móvel se desloca de uma distância
x, o bloco B desloca-se de 2x e, portanto:
aB
=2
aB = 2aA ⇒ ––––
aA
F = (mA + mB + mC) a
F = (0,3 + 0,2 + 1,5) 15 (N)
F = 30N
Respostas: a) 3,0N
b)
b) 15m/s2
c) 30N
n Módulo 18 – Aplicações
das Leis de Newton
1)
a)
PFD (bloco):
P – Fdin = ma
20 – 15 = 2,0 . a
PFD (A): 2T = mA a
(1)
PFD (B): PB – T = mB 2a (2)
a = 2,5m/s2
↓→
a
(2) x 2: 2PB – 2T = 4 mB a (3)
(1) + (3): 2PB = (mA + 4mB) a
2 . 50 = (20 + 4 . 5) a
100 = 40 . a ⇒
a = 2,5m/s2
aA = 2,5m/s2 e aB = 5,0m/s2
b) O sentido do movimento não está determinado.
c) 2T = mA a
O elevador pode estar:
2T = 20 . 2,5 ⇒
T = 25N
→
→
a ↓↓V
descendo com movimento acelerado
→
→
a ↓↑V
subindo com movimento retardado
d)
c) P – F = ma
mg – ma = F
F = m (g – a)
F1 = 2T = 50N
Respostas: a)
F2 = T
2 = 25
2N
aB
–––– = 2
aA
b) aA = 2,5m/s2 e aB = 5,0m/s2
c) 25N
↓→
a ⇔ gap = g – a
↑→
a ⇔g =g+a
ap
gap = g – a = 7,5m/s2
Respostas: a) a = 2,5m/s2; para baixo
b) pode estar descendo com movimento acelerado ou subindo com movimento retardado.
c) 7,5m/s2
d) 50N e 25
2N
–5
2)
a)
PFD (A + B): PB – PA = (mA + mB)a
Aplicando-se a 2.ª Lei de Newton ao
bloco, vem:
P – Fdin = ma
mg – ma = Fdin
Fdin = m (g – a) = m gap = Paparente
30 – 20 = 5,0 . a
a = 2,0m/s2
b) Em (1):
gaparente
T – 20 = 2,0 . 2,0 ⇒
Fdin = 10 . 8,0 (N) ⇒ Fdin = 80N
b)
Respostas: a) 2,0m/s2
b) 24N
1) ↑ →
v : subindo com movimento retardado.
→
a↓
2) ↓ →
v : descendo com movimento acelerado.
T = 24N
5)
1)
c) queda livre: a = g ⇒ gap = g – a = 0 ⇒ Pap = 0 = Fdin
Respostas: a) 80N
b) pode estar subindo com movimento retardado, ou descendo com movimento acelerado.
c) zero
3)
a)
PFD (bloco):
Fdin – mg = ma
Fdin = m (a + g)
gaparente
Fdin = 2,0 . 12,0 (N)
Fdin = 24,0 N
1) PFD (A): T – PA = MAaA
⇒
30 – 10 = 1,0 aA
aA = 20m/s2
2) PFD (B): T – PB = MBaB
⇒
30 – 20 = 2,0 aB
aB = 5,0m/s2
A aceleração da polia tem módulo dado por:
aA + aB
aP = ––––––––––
2
20 + 5,0
aP = ––––––––– (m/s2) ⇒ aP = 12,5 m/s2
2
b) ↑ →
a ⇒ gap = g + a = 12,0m/s2
c) ↑ →
a=
{
→
1) ↑ V subindo com movimento acelerado
→
2) ↓ V descendo com movimento retardado
d) s = V0t + –– t2 (MUV)
2
Resposta: C
6)
a) 1) Cálculo da aceleração dos blocos A e B:
PFD (A + B): PA – PB = (mA + mB) a
30,0 – 20,0 = 5,0 . a ⇒ a = 2,0 m/s2
12,0
1,5 = 0 + ––––– T2
2
2) s = V0 t + –– t2
2
T2 = 0,25 ⇒ T = 0,50s
Respostas: a) 24,0N
b) 12,0m/s2
c) ou subindo com movimento acelerado ou
descendo com movimento retardado
d) 0,50s
4)
2,0
16,0 = 0 + ––– tA2 ⇒
2
tA = 4,0s
b) 1) Velocidade escalar de B quando A atinge o solo:
V2 = V02 + 2 s
VB2 = 0 + 2 . 2,0 . 16,0 ⇒ VB = 8,0 m/s
2) Distância percorrida por B depois que A chega ao solo:
a)
V2 = VB2 + 2 s
0 = 64,0 + 2(–10,0) s
20,0 s = 64,0s
s = 3,2 m
6–
PFD (A): T – PA = mAa
(1)
PFD (B): PB – T = mBa
(2)
3) Hmáx = H0 + s
9)
Hmáx = 16,0 + 3,2 (m)
Hmáx = 19,2 m
Respostas: a) 4,0s
7)
b) 19,2m
a) Para um referencial no elevador, temos:
s = V0t + –– t2
2
1,6 = –– (0,8)2
2
3,2
= ––––– (m/s2) ⇒
0,64
PFD (E): TA – PE = mE a
PFD (CP): TB + PB – TA = mCP a
(1)
(2)
Como mE = mCP = m, vem:
(1) + (2): TB = 2m a
TB = 10,0 . 102 . 1,0 (N)
= 5,0m/s2
Esta aceleração corresponde à gravidade aparente e,
como é menor que a gravidade real (10,0m/s2),
concluímos que a aceleração do elevador é dirigida para
baixo e de módulo a dado por:
TB = 1,0 . 103N
Resposta: A
10) PFD (andaime + lavador):
3F – Mg = Ma
gap = g – a
5,0 = 10,0 – a ⇒
M (a + g) 160 . 10,5
F = –––––––– = ––––––––– (N)
3
3
a = 5,0m/s2
b) A balança indica o peso aparente da pessoa:
Pap = m gap
Pap = 70 . 5,0 (N) ⇒
F = 560N
Pap = 350N
c) Para um referencial no elevador, temos:
V = V0 + t
Vrel = 0 + 5,0 . 0,8 (m/s)
Vrel = 4,0m/s
d)
Resposta: D
A velocidade resultante (relativa ao
solo terrestre) é a soma vetorial da
velocidade relativa (4,0m/s) com a
velocidade de arrastamento do
elevador (4,0m/s) e, como os sentidos
são opostos, ela será nula.
→
VR = 0
Respostas: a) 5,0m/s2; para baixo
c) 4,0m/s
b) 350N
d) zero
FRENTE 2 ÓPTICA
n Módulo 15 – Translação de um Espelho
Plano e Número de
Imagens
1)
O ângulo entre os dois espelhos vale = 90°.
360°
Para um dos vasos, temos N = –––– – 1; N = 3 imagens.
90°
8)
Como são dois vasos, teremos 6 imagens de vasos mais os 2
vasos originais, gerando 8 vasos na foto.
Resposta: E
2)
Aplicando-se a 2.a Lei de Newton:
Bloco A: P – T = ma (1)
Bloco B: 2T – P = ma (2)
(1) + (2) + (3): P = 3ma
Resposta: C
a = g/3
360°
N = –––– – 1
360°
7 = –––– – 1
360°
8 = –––– ⇒ 8 . = 360°
Bloco C: P – T = ma (3)
mg = 3ma ⇒
Se, com 3 bailarinas, gera-se uma cena com 24 imagens,
24
significa que cada bailarina aparece ––– = 8 vezes na cena.
3
Para a mesma bailarina, teremos então 8 – 1 = 7 imagens
formadas pelos espelhos. Logo:
↑→
a
360°
= –––– = 45°
8
Resposta D
–7
3)
π
= 45° = –––
4
a)
π
O ângulo = –– representa o desvio entre as imagens ocasio4
nado pela rotação do espelho de um ângulo . Como = 2,
resulta que = ––
2
π
= ––
8
Resposta: E
6)
b)
c) Do esquema (a), vem:
d1,2 = 6,0m
d2,3 = 4,0m
d3,4 = 6,0m
4)
As retas N1 e N2 são perpendiculares aos espelhos E1 e E2,
respectivamente. Com isso, podemos assegurar que + são
ângulos internos ao triângulo da figura. Como + + 60° = 180°,
temos = 120° – .
Resposta: E
n Módulo 16 – Raios Notáveis e
Construção de Imagens
nos Espelhos Esféricos
1)
Girar o espelho ao longo do eixo perpendicular indicado não
altera a imagem.
Resposta: C
5)
No espelho convexo, raios que incidem sobre o centro de curvatura (i1) refletem-se retornando sobre si mesmos (r1).
No espelho convexo, raios que incidem sobre o foco (i2) refletem-se retornando paralelamente ao eixo principal (r2).
Resposta: B
2)
Como OM = MN = d e em M temos um ângulo reto, o
triângulo OMN é isósceles. Temos então que 2 + 90° = 180°
= 45°:
8–
No espelho côncavo, raios que incidem sobre o centro de
curvatura (AC) refletem-se retornando sobre si mesmos.
No espelho côncavo, raios que passam pelo foco (AF)
refletem-se retornando paralelamente ao eixo principal.
Logo, a única alternativa válida é a A.
Resposta: A
6)
3)
Na ilustração, colocamos o objeto (por exemplo, um prego)
entre o foco e o vértice do espelho côncavo. Para construir
sua imagem, basta utilizar 2 dos 4 raios notáveis conhecidos.
Escolheu-se desenhar:
• raio que incide no vértice com ângulo reflete-se com
mesmo ângulo ;
• raio que passa pelo foco reflete-se paralelamente ao eixo
principal.
Como os raios refletidos não se encontram, desenhamos
seus prolongamentos. Como os prolongamentos dos raios
refletidos se encontram, a imagem é virtual. Da figura, vemos
que a imagem em p’ é maior e tem a mesma direção do
objeto.
Obs.: Pode-se verificar que o desenho dos outros raios notáveis fornece a mesma imagem.
Resposta:
Em um automóvel, deseja-se jogar a luz do farol o mais longe
possível, iluminando objetos distantes. Isso significa que os
raios precisam sair de forma paralela do carro. Apenas
colocando o filamento sobre o foco de um espelho côncavo
conseguimos esse efeito.
Resposta: B
4)
Na ilustração, colocamos o prego entre o foco e o vértice do
espelho côncavo. Para construir sua imagem, basta utilizar 2
dos 4 raios notáveis conhecidos.
Escolheu-se desenhar:
• raio que incide no vértice com ângulo reflete-se com
mesmo ângulo ;
• raio que passa pelo foco reflete-se paralelamente ao eixo
principal.
Como os raios refletidos não se encontram, desenhamos
seus prolongamentos. Como os prolongamentos dos raios
refletidos se encontram, a imagem é virtual. Da figura, vemos
que a imagem em p’ é maior e tem a mesma direção do
objeto.
Obs.: Pode-se verificar que o desenho dos outros raios notáveis fornece a mesma imagem.
Resposta: D
5)
Os espelhos que aumentam o campo visual, por possibilitarem a visão de imagens diminuídas do ambiente, são os
espelhos convexos. Estes fornecem sempre o mesmo tipo de
imagem de um objeto real: virtual, menor, direita.
Resposta: B
7)
I. Verdadeira. No espelho côncavo, a classificação da
imagem depende da posição do objeto em relação ao
espelho. Não terá, portanto, uma classificação única. A
imagem ora será real e invertida, ora será virtual e direita,
ou não invertida.
II. Verdadeira. Os espelhos que aumentam o campo visual,
por possibilitarem a visão de imagens diminuídas do
ambiente, são os espelhos convexos. Estes fornecem
sempre o mesmo tipo de imagem de um objeto real:
virtual, menor, direita.
III. Falsa. No espelho plano, a imagem é sempre virtual, pois
resulta dos prolongamentos dos raios refletidos.
Resposta: D
n Módulo 17 – Estudo Analítico dos
Espelhos Esféricos
1)
Para descobrir a distância entre as imagens, precisamos
primeiro encontrar as posições delas, p’A e p’B. Da figura, podemos obter a distância focal do espelho, f = 5cm + 5cm =
10cm, além das distâncias de cada objeto em relação ao
espelho, pA = 5cm e pB = 15cm. Com a Equação de Gauss,
encontraremos a posição de cada imagem.
–9
Objeto A: 1
1
1
–– = ––– + –––
p’A
f
pA
Obs: A maioria dos exercícios desta seção exige conhecimento de propriedades de frações e de equações fracionárias e é
o mínimo que se espera de alunos do Ensino Médio.
Resposta: B
1
1
1
–– = –– + –––
10
5
p’A
1
1
1
–– – –– = –––
10
5
p’A
3)
1
2
1
–– – ––– = –––
10
10
p’A
a) Para calcular a distância entre o passageiro e sua imagem,
d = p – p’ , primeiro precisamos da posição da imagem p’.
Temos que p = 3,0m, R = 4,0m e com este valor descobrimos
R
4,0
a distância focal f = –– ; f = ––– m = 2,0m. Como o espelho
2
2
1
1
– ––– = –––
10
p’A
é convexo, f = –2,0m
p’A = –10cm
1
1
1
–– = –– + ––
f
p
p’
Objeto B: 1
1
1
–– = ––– + –––
f
pB
p’B
1
1
1
– –– = –– + ––
2
3
p’
1
1
1
–– = –– + –––
10
15
p’B
1
1
1
– –– – –– = ––
2
3
p’
1
1
1
–– – –– + –––
10 15
p’B
3
2
1
– –– – –– = ––
6
6
p’
3
2
1
–– – –– = –––
30 30
p’B
1
5
–– = – ––
p’
6
1
1
––– = –––
30
p’B
p’ = –1,2m
E a distância d vale: d = 3 – (–1,2) (m)
p’B = 30cm
d = 4,2m
b) Como o passageiro tem altura o = 1,6m, para encontrar a
altura da imagem i, usamos:
i
–p’
–– = ––
o
p
i
–(–1,2)
––– = ––––––
1,6
3
No esquema, vemos que a distância entre as imagens será de
40cm.
Resposta: D
2)
i
––– = +0,4
1,6
i = 1,6 . 0,4 (m)
Para encontrar a distância da imagem ao espelho p’, podemos
utilizar a Equação de Gauss, dado que p = 40cm e que a distân30
cia focal vale metade do raio de curvatura, f = ––– cm = 15cm.
2
1
1
1
–– = –– + ––
f
p
p’
1
1
1
–– = –– + ––
15 40
p’
1
1
1
–– – –– = ––
15 40
p’
8
3
1
–––– – –––– = ––
120
120
p’
1
5
–– = –––
p’
120
120
p’ = ––– cm
5
p’ = 24cm
10 –
i = 0,64m
4)
O exercício deseja encontrar a distância entre o objeto e sua
imagem, d = p – p’ . Precisamos encontrar p’.
A distância entre o foco e o centro de curvatura do espelho
corresponde à distância focal f. Logo, da figura, temos que
f = 10cm + 15cm; f = 25cm. A distância do objeto ao espelho
p será dada pela soma da distância entre o vértice e o foco,
uma distância focal, com 10cm: p = 25cm + 10cm; p = 35cm.
Logo:
1
1
1
–– = –– + ––
f
p
p’
1
1
1
––– = ––– + ––
25
35
p’
1
1
1
––– – ––– = ––
25
35
p’
3)
7
5
1
–––– – –––– = ––
175
175
p’
1
2
–– = ––––
p’
175
nA,B
p’ = 87,5cm e d = 35 – 87,5 (m)
c
––––
nA
VA
= –––– = ––––
c
nB
––––
VB
VB
1,8 . 108m/s
nA,B = ––––
= –––––––––––––
VA
2,4 . 108m/s
nA,B = 0,75
d = 52,5cm
Resposta: D
5)
c
I) Verdadeira, pois, como n = ––– e V < c, temos n > 1.
V
II) Verdadeira.
III) Verdadeira.
O aumento linear vale A = 2 e p = 50cm.
Resposta: D
f
A = ––––
f–p
4)
(f)
2 = ––––––
(f – 50)
nágua
nágua
nágua, vidro = –––––––
= –––––––
nvidro
c
–––––––
Vvidro
nágua Vvidro
nágua, vidro = –––––––––––––
c
2 . (f – 50) = f
2f – 100 = f
4
–– VVidro
8
3
–– = ––––––––
9
3,0 . 108
f = 100cm
R
Como f = ––
2
Vvidro = 2,0 . 108m/s
r=2.f
Resposta: B
r = 200cm = 2m
Como r = 2m é positivo, o espelho é côncavo.
5)
Como r2 e r3 estão no mesmo meio (II), são raios incidente e
refletido respectivamente e, como r1 se encontra no meio (I),
é o raio refratado. A figura mostra que, quando a luz se
propaga do meio (II) para o meio (I), o raio refratado se aproxima da normal no ponto de incidência, evidenciando que a
luz se propagou do meio menos refringente para o meio mais
refringente.
Resposta: B
6)
Do meio (1) para o meio (2), a luz se desvia afastando-se da
normal no ponto de incidência; portanto, n1 > n2. Ao se propagar do meio (2) para o meio (3), a luz se desvia aproximando-se da normal no ponto de incidência; portanto n3 > n2.
Observando também que o ângulo de incidência no meio (1)
é maior do que o ângulo de refração no meio (3), concluímos
que n1 < n3. Ordenando esses três valores, temos:
n3 > n1 > n2
Resposta: E
7)
Os ângulos de incidência i e de refração R são, respectivamente, os ângulos complementares a 30° e a 60°:
Resposta: B
n Módulo 18 – Índice de Refração
e Leis da Refração
1)
O índice de refração absoluto n para uma luz monocromática
em um certo meio óptico ordinário é dado por:
c
n = –––
V
em que c é o módulo da velocidade da luz no vácuo, que é
constante para qualquer cor, e V o módulo da velocidade da
luz no meio. Tal velocidade, por sua vez, depende da natureza
do meio e da frequência (cor) da luz.
Resposta: A
2)
O índice de refração absoluto n para uma luz monocromática
em um certo meio óptico ordinário é dado por:
c
n = –––
V
i = 60° e R = 30°
4
Como V = ––– c, temos:
5
Aplicando a Lei de Snell-Descartes, temos:
c
5
n = ––– = –––
4
4
––– c
5
nar sen (60°) = nLíq sen (30°)
1
3
1,0 . –––– = nLíq . ––––
2
2
n = 1,25
nLíq = 3
Resposta: B
n1 sen i = n2 sen R
Resposta: D
– 11
8)
Impondo-se que o somatório dos torques em relação ao
apoio (2) seja nulo, temos:
a) Aplicando a Lei de Snell-Descartes, temos:
n1 sen i = n2 sen R
PP . d = PC . x
nar sen (53°) = nLíq sen (37°)
2mg . d = mg . x
1,0 . 0,80 = nLíq 0,60
x = 2d
4
nLíq = ––
3
Resposta: B
b)
5)
Para o equilíbrio, o somatório dos torques das forças em
relação ao centro de gravidade do avião deve ser nulo.
PD . dD = 2 PT . dT
MD . 16,0 = 2 MT . 4,0
MT = 2MD
FRENTE 3 – MECÂNICA E ELETRICIDADE
Como a massa total é 90t, vem:
MD + 2 MT = 90t
n Módulo 15 – Estática do Corpo Extenso
MD + 2 . 2 MD = 90t
1)
5MD = 90t ⇒
1) Resultante nula
2) As três forças concorrem no
ponto Y para que o torque
resultante seja nulo.
MD = 18t
MT = 36t
Resposta: C
6)
Resposta: D
2)
Sendo o objeto mais denso que a água, o peso no prato da
jarra B aumenta e o sistema tende a girar no sentido horário.
Isso faz com que o fio f1 fique tenso (T1 = PB’ – PA, supondo-se
que haja simetria de posições das jarras) e o fio f2 continua
sem tensão.
Resposta: C
3)
Para o equilíbrio, o somatório dos torques, em relação ao
ponto G, deve ser nulo:
PI dI + PK dK = PA . dA
40 . g 2d + mK g 4d = 60g . 6d
80 + 4mK = 360
4mK = 280 ⇒ mK = 70 gramas
Resposta: B
4)
A prancha começa a tombar quando a força aplicada pelo
apoio (1) se anula.
a) 1) Para o equilíbrio do caminhão, o somatório dos
torques em relação ao centro de massa C do caminhão
é nulo e portanto:
F2 d2 = F1 d1
F2 . 4,0 = 1,0 . 105 . 2,0
F2 = 5,0 . 104N = 0,5 . 105N
2) A condição de força resultante nula é:
P = F1 + F2
P = 1,5 . 105N
b) De acordo com a 3.a Lei de Newton (ação e reação), o caminhão exerce na 2.a balança uma força vertical, para baixo e
de módulo igual a 5,0 . 104N.
Observação:
O item (a) pode ser resolvido sem calcular F2, tomando-se os
torques em relação ao ponto de aplicação de F2.
P . dP = F1 dF
1
P . 4,0 = 1,0 . 105 . 6,0
12 –
P = 1,5 . 105N
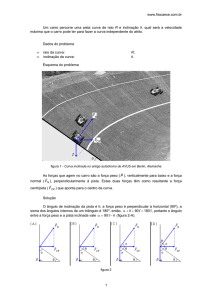
Atração
Figuras 1 e 2
Repulsão
Figura 3
Nesse caso, o valor de F2 seria obtido pela relação:
F1 + F2 = P
Respostas: a) 1,5 . 105N
b) vertical, para baixo e de módulo 5,0 . 104N
7
Para o equilíbrio, a soma dos torques em relação ao ombro
de Nivaldo deve ser nula; isso ocorre na opção (a).
Torques em relação a O:
M1 = P . d + P . 2d = 3Pd
M2 = P . 3d
Resposta: D
M1 = M2
2)
Resposta: A
8)
Resposta: A
1) Somatório dos torques nulo em relação a M:
P . d1 + PP d2 = FJ . d3
3)
300 . 1,0 + 60 . 1,5 = FJ . 3,0
FJ = 100 + 30 (N) ⇒
FJ = 130N
2) Resultante nula:
FM + FJ = P + PP
FM + 130 = 360
FM = 230N
Resposta: B
Resposta: E
n Módulo 16 – Campo Magnético
e Força de Lorentz
4)
1)
Na situação acima, há repulsão; logo, A é polo Sul.
Partindo o ímã AT, temos:
Portanto, haverá repulsão nas experiências 1 e 3 e atração
nas experiências 2 e 4.
Resposta: A
– 13
5)
Usando a Regra da Mão Esquerda (RME):
6)
Usando a Regra da Mão Esquerda (RME):
9)
a) e b)
10)
7)
→
Figura 9: O ângulo de inclinação entre o campo B e a velocidade é nulo. Então:
F = q . v . B . sen 0°
F=0
Figura 10: O ângulo de inclinação é 180°, logo:
F = q . v . B . sen 180°
RME para carga negativa:
Usando a regra da mão esquerda, temos que a força magnética está entrando no plano, o que desvia o elétron para
dentro do plano da figura.
Resposta: D
F=0
11) Usando a regra da mão esquerda para carga negativa, temos:
8)
= 45°
2
sen = –––––
2
a) →
Fm
b) Então:
Fm = q . v . B . sen 45°
2
Fm = 3 . 10–12 . 1 . 4 . 108 . –––– (N)
2
Fm = 62 . 10–4N
14 –
Resposta: A
→ →
→
12) Em relação aos vetores →
v , B e F , temos que F é perpen→ →
dicular a B e v .
Resposta: C
4)
Usando a regra da mão esquerda, determinamos o sentido
da força magnética na carga positiva.
13)
Resposta: E
14) Paralelamente ao campo magnético, encontra-se a velocidade.
Então = 0
Assim, a carga I é positiva (próton).
A carga negativa recebe força no sentido oposto:
Fm = q . v . B . sen 0°
Fm = 0
Resposta: B
n Módulo 17 – Movimento de uma
Partícula Eletrizada em um
Campo Magnético
Uniforme
1)
Com isso, conclui-se que a carga III é um elétron.
Como a carga II não sofre alteração em sua trajetória,
percebe-se que ela é um nêutron.
Resposta: E
Uma partícula eletrizada sob ação de um campo magnético
sofre uma força magnética dada pela expressão:
→
→ →
Fm = q . v . B . sen se
5)
= 0 ou = 180° ⇒ Fm = 0
0 ou 180°
Pela regra da mão esquerda, determinamos o sentido da
força magnética em cada carga.
⇒ Fm 0
→
→
O fato da força Fm ser perpendicular aos vetores v e B faz a
força magnética ser a resultante centrípeta sobre a carga
elétrica; logo, ela não altera o módulo da velocidade e sim
sua direção.
Daí se conclui que, em qualquer caso, a partícula terá um
movimento uniforme.
Resposta: E
2)
→
→
→
Sendo Fm = q . v . B . sen , se v = 0, temos que Fm 0, então
a partícula permanecerá em repouso.
Resposta: C
3)
m.V
6,4 . 10–25 . 5 . 106
0) (V) R = –––––– ; R = –––––––––––––––––– (m)
앚q앚B
3,2 . 10–16 . 5 . 10–1
Na carga positiva:
Logo, a carga X é o posítron.
R = 2 . 10–2m = 2cm
1) (V) Fm = q V B sen , como = 90° (do enunciado) ⇒ Fm 0
e constante (força centrípeta).
Na carga negativa:
2) (F) A força centrípeta altera a direção da velocidade.
3) (F) O trabalho da força centrípeta é nulo, pois o ângulo
dela com o deslocamento vale 90°.
4) (V) Como o módulo da velocidade é constante a energia
cinética Ec é constante.
Resposta: B
Assim, a carga Z é o elétron.
Na carga neutra, a força magnética é nula, portanto, a carga
Y é o nêutron.
Resposta: B
– 15
6)
Como a velocidade é perpendicular ao campo magnético, a
trajetória é uma semicircunferência (devido à limitação do
campo). Assim, a força magnética é uma força centrípeta.
Fm = Fcp
m . V2
q . V . B . sen = –––––– (sen = 1)
R
m.V
q . B = ––––––
R
107
q
V
––– B = ––– ⇒ 108 . B = –––– m
R
2
7)
9)
a) O trabalho da força magnética é nulo, pois essa força é
perpendicular ao deslocamento (Fm = Fcp).
b) Como a força magnética equivale à força centrípeta,
temos:
Fcp = Fm
m . V2
–––––– = q V B sen R
B = 5 . 10–2 T
Com a regra da mão esquerda, determinamos o sentido da
força magnética sobre cada partícula.
(sen = 1, pois = 90°)
R.q.B
V = –––––––––
m
10) Do enunciado, temos:
→ →
O ângulo entre B e V é = 0°,
→ →
logo: Fm = 0
Daí, tem-se que o vetor velocidade não se altera,
o elétron permanecerá em movimento retilíneo
uniforme.
Resposta: D
8)
a) O raio da trajetória é dado por:
m.V
R = ––––––––
앚q앚.B
Como V e R são diretamente proporcionais, se R’ = R/2
m
V’ = V/2, assim: V’ = 3 . 105 –––
s
b) Como a trajetória é uma semicircunferência, a força
magnética aponta para o centro da circunferência.
Resposta: E
11) a) A carga q pode ser positiva ou negativa; em qualquer
caso, a força magnética é equivalente à força centrípeta.
Pela regra da mão esquerda, percebemos que o campo
magnético deve ser perpendicular ao plano do papel
(entrando ou saindo, dependendo do sinal da carga q).
b) Pelo teorema da energia cinética:
τFm = EC
τFm =
EC – EC , como
τFm= 0, pois Fm = Fcp
final inicial
e a força centrípeta não realiza trabalho, temos:
0=
EC –
final
c) Pela regra da mão esquerda, se a carga for positiva, o
campo magnético sairá do plano do papel.
EC
inicial
⇒ EC
inicial
=
EC
→
앚→
u 앚 = 앚V앚
final
12) A partícula fica sujeita a uma força resultante dada pela soma
→ → →
das forças elétrica e magnética ( FR = Fel + Fm ). Como o movimento da partícula é retilíneo e uniforme (do enunciado),
→ →
→
→
significa que FR = 0, assim Fel = – Fm , portanto:
→
→
Fel = Fm q.E=q.V.B
E=V.B
500 = V . 0,10 V = 5 . 103m/s
Resposta: D
16 –
n Módulo 18 – Movimento de uma
Partícula no Campo e
Condutor Retilíneo
3)
A força magnética que atua num condutor retilíneo é dada
por:
Fm = B . i . ᐉ . sen a) Do enunciado, = 0° ou = 180° ⇒ sen = 0 1)
Fm = 0
b) = 90° ⇒ Fm = 2 . 104 . 2 . 0,2 . 1 (N) Fm = 8 . 103N
4)
A força magnética é dada por: Fm = B . i . ᐉ . sen Assim:
1
Fm = 10–3 . 4 . 0,5 . ––– (N)
2
Fm = 10–3N
Resposta: D
2)
Com a regra da mão esquerda, determinamos a direção e o
sentido da força magnética em cada trecho da espira.
Por simetria, temos:
→
→
Fm = Fm e
1
→
3
→
Fm = Fm 2
assim:
4
→
→
FR = 0
(a força resultante é nula)
Por simetria, temos também que x1 = x2 e y1 = y2; com isso,
o torque da força magnética 1 é cancelado pelo torque da
força magnética 3, da mesma forma que são cancelados os
torques no eixo x; por isso, o torque total é nulo.
Resposta: B
– 17