Física I – Resolução

Física I – Resolução
4. D
De acordo com as informações, obtemos o seguinte esquema:
Capítulo 9
L
Lentes esféricas
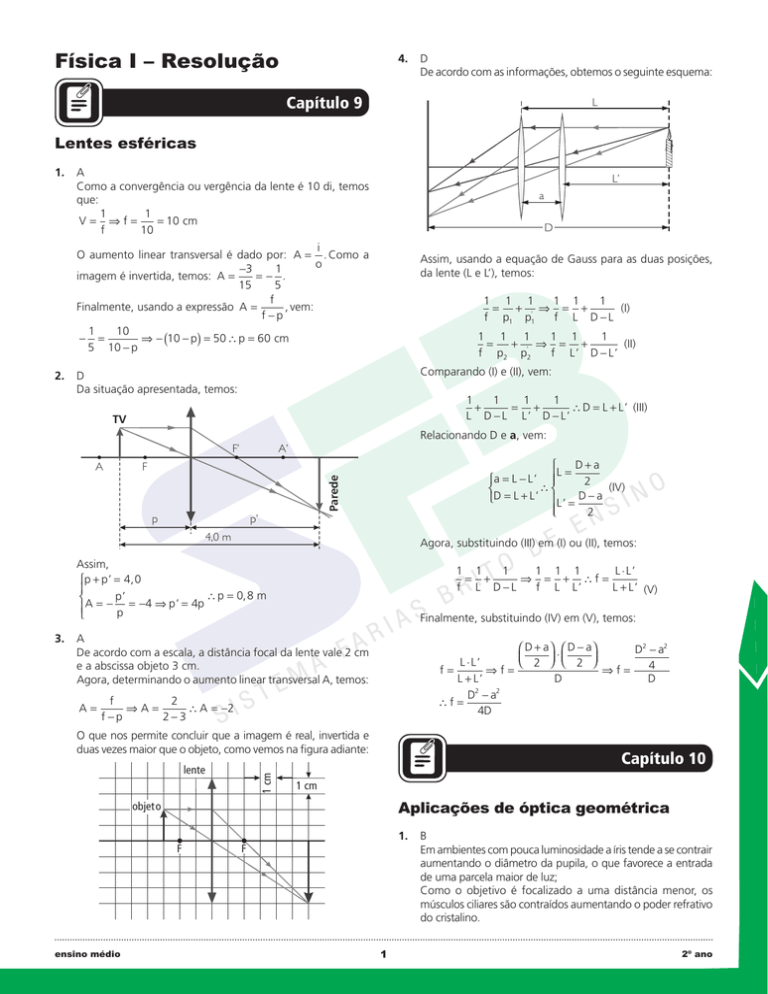
1. A
Como a convergência ou vergência da lente é 10 di, temos
que:
1
1
V= ⇒f=
= 10 cm
f
10
L’
a
i
O aumento linear transversal é dado por: A = . Como a
o
−3
1
imagem é invertida, temos: A =
=− .
15
5
f
Finalmente, usando a expressão A =
, vem:
f −p
1
10
− =
⇒ − (10 − p) = 50 ∴ p = 60 cm
5 10 − p
1 1 1
1 1
1
=
+
⇒ = +
(II)
f p2 p’2
f L’ D − L’
Comparando (I) e (II), vem:
1
1
1
1
+
= +
∴ D = L + L ’ (III)
L D − L L’ D − L’
TV
F’
Parede
F
p’
4,0 m
Assim,
p + p ’ = 4, 0

∴ p = 0, 8 m
p’

A = − p = −4 ⇒ p ’ = 4p

O que nos permite concluir que a imagem é real, invertida e
duas vezes maior que o objeto, como vemos na figura adiante:
1 cm
Finalmente, substituindo (IV) em (V), temos:
Capítulo 10
1 cm
Aplicações de óptica geométrica
objeto
F
ensino médio
Agora, substituindo (III) em (I) ou (II), temos:
 D + a  D − a
D2 − a2
⋅



 2   2 
L ⋅L’
4
⇒f=
⇒f=
f=
D
L + L’
D
D2 − a2
∴f =
4D
f
2
⇒A=
∴ A = −2
f −p
2−3
lente
D+a

L=
a = L − L ’ 
2
∴
(IV)

D = L + L ’ L ’ = D − a

2
L ⋅L’
1 1
1
1 1 1
= +
⇒ = + ∴f =
f L D−L
f L L’
L + L ’ (V)
3. A
De acordo com a escala, a distância focal da lente vale 2 cm
e a abscissa objeto 3 cm.
Agora, determinando o aumento linear transversal A, temos:
Relacionando D e a, vem:
A’
p
A=
Assim, usando a equação de Gauss para as duas posições,
da lente (L e L’), temos:
1 1 1
1 1
1
= + ⇒ = +
(I)
f p1 p1’
f L D−L
2. D
Da situação apresentada, temos:
A
D
1. B
Em ambientes com pouca luminosidade a íris tende a se contrair
aumentando o diâmetro da pupila, o que favorece a entrada
de uma parcela maior de luz;
Como o objetivo é focalizado a uma distância menor, os
músculos ciliares são contraídos aumentando o poder refrativo
do cristalino.
F
1
2º ano
2. E
Luneta astronômica ou luneta de Galileo são outras
designações para o telescópio refrator, que estudamos ao
longo desse capítulo.
O sistema é dito afocal quando o foco imagem da lente
objetiva (Fob) coincide com o foco objeto da lente ocular
(Foc), conforme a figura adiante:
objeto
no infinito
objetiva
A2 =
ocular
fob
foc
F’ob. ≡ Foc.
F’oc
d = fob. + foc.
Logo, o aumento linear transversal total é:
A = A1 · A2 ⇒ A = 0,2x –2 ∴ A = –0,4
O que nos permite concluir que a imagem final é real e o seu
aumento é 0,4.
A = A ob. ⋅ A oc. ⇒ −500 = −100 × A oc. ∴ A oc. = 5
Para lente objetiva, temos:
1 1 1
1
1
1
= + ⇒ =
+
∴ p’ob. = 202 mm
f p p’
2 2, 02 p’ob.
Assim, como o aumento angular M = 30, temos que:
A ob. =
fob.
f
⇒ 30 = ob. ∴ fob. = 150 cm
foc.
5
Logo,
A = A1 · A2
− p’oc.
− p’oc.
⇒
= 5 ∴ p’oc. = −20 cm
poc.
4
Deste modo, a imagem do vírus será observada a 20 cm da
lente ocular.
O aumento linear transversal da primeira lente (A1) é:
A1 =
f1
−20
∴ A1 = 0, 2
⇒ A1 =
−20 − 80
f1 − p1
Determinando a abscissa imagem para a primeira lente, vem:
1 1 1
1
1
1
= + ’ ⇒
=
+ ’ ∴ p1’ = −16 cm
f1 p1 p1
−20 80 p1
Para lente ocular, temos:
A oc. = 5 =
3. A
O aumento linear transversal total (A) é dado pelo produto
dos aumentos lineares transversais de cada uma das lentes,
ou seja:
− p’ob.
−202
⇒ A ob. =
∴ A ob. = −100
2, 02
pob.
poc. = 24,2 – 20,2 = 4 cm
d = 150 + 5 ∴ d = 155 cm
f2
20
⇒ A2 =
∴ A1 = −2
f2 − p2
20 − 30
4. E
De modo que o comprimento da luneta (d) é a soma das
distâncias focais das lentes, ou seja:
M=
Então, o aumento linear transversal para a lente convergente é:
Capítulo 11
Acústica: som e suas características
1. C
A relação entre o nível sonoro β é a intensidade I, é dada por:
β
 I
β = 10 log   ⇒ I = I0 ⋅ 1010
 I0 
Como essa abscissa é negativa, concluímos que a imagem
é vertical, logo encontra-se do mesmo lado do objeto e,
portanto a 30 cm da lente convergente, como vemos na
figura adiante:
Comparando as intensidades sonoras antes (I1) e depois (I2),
temos:
β1
1
( β1 − β2 )
I1 I0 ⋅ 1010
I1
10
=
10
⇒
=
β2
I2
I2
I0 ⋅ 1010
objeto
14 cm
80 cm
Assim, uma redução de 30 dB (β2 – β1 = –30 dB) reduz a
intensidade do som a:
1
( −30 )
I1
I
= 1010
⇒ 1 = 10−3
I2
I2
Ou seja, a intensidade do som deve ser 1.000 vezes menor.
16 cm
ensino médio
2
2º ano
2. B
Apesar de estar dentro da faixa audível, o som cuja frequência
é 0,1 kHz ou 100 Hz não pode ser ouvido, por apresentar
nível muito baixo, 10 dB, conforme o gráfico fornecido.
Agora, vamos utilizar a fórmula de Doppler:
 v ± vO 
 −
f’ =  S
⋅ f →   [afastamento]
 +
 v S ± vF 
 330 − 3, 3
f’ = 
⋅ 2000 ∴ f ’ = 1980 Hz
 330 + 0 
Logo, o som que o atleta ouve tem frequência aparente:
f’ = 1980 Hz
3. D
De acordo com o enunciado, cada uma das curvas do gráfico
representa os limites inferiores dos sons audíveis para cada
ouvido, de modo que a região sob cada curva representa
silêncio para aquele ouvido.
Analisando cada um dos itens, concluímos que o indivíduo
consegue ouvir sussurros (sons de baixo nível sonoro) apenas
com o ouvido direito.
4. A
De acordo com o enunciado, o primeiro trem será a fonte,
enquanto o segundo, o observador, de onde podemos
concluir:
vF = 72 km/h = 20 m/s
vo = 54 km/h = 15 m/s
Assim, utilizando a fórmula de Doppler, vem:
 v ± vO 
 +
f’ =  S
⋅ f →   [aproximação]
 −
 v S ± vF 
4. B
 I
 I 
 I 
β = 10 log   ⇒ 50 = 10 log  −12  ⇒ log  −12  = 5


 10 
10
 I0 
I
= 105 ∴ I = 10−7 W / m2
10−12
I=
 340 + 15 
f’ = 
⋅ 600 ∴ f ’ ≈ 665, 6 Hz
 340 − 20 
Pot.
Pot.
⇒ 10−7 =
∴ Pot. = π ⋅ 10−3 W
A
4 π × 502
Capítulo 12
Efeito Doppler
1. A
 v + v0 
 v + v0 
v + v0
v
f’ =  S
⋅ f ⇒ 2f =  S
⋅f ⇒ S
= 2∴ 0 = 1


v
−
v
v
−
0
v
vS
 S
 S

S
F
2. A
Dados:
f = 20 kHz (frequência da fonte)
f’ = 22,5 kHz (frequência percebida pelo veículo)
d = 50 m (distância entre o veículo e o obstáculo)
Estando o objeto fixo, as ondas que o atingem retornam com
a mesma velocidade, ou seja, vF = vO = v.
Usando equação de Doppler, temos:
 v ± vO 
 +
f’ =  S
⋅ f →   [aproximação]
 −
 v S ± vF 
 340 + v 
22, 5 × 103 = 
⋅ 20 ⋅ 103 ∴ v = 20 m / s
 340 − v 
Deste modo,
50
∆S
v=
⇒ 20 =
∴ ∆t = 2, 5 s
∆t
∆t
3. B
Inicialmente vamos determinar a componente da velocidade
do atleta em relação ao raio de onda da fonte:
Ux = U ⋅ cos θ ⇒ Ux = 6, 6 ⋅ cos 60° ∴ Ux = 3, 3 m/s
A frequência do som produzido é:
v = λ ⋅ f ⇒ 330 = 16, 5 ⋅ 10−2 × f ∴ f = 2.000 Hz
ensino médio
3
2º ano