Capitulo 8.Subespaços Invariantes

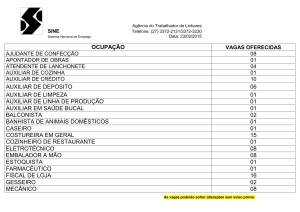
Subespaços Invariantes
Seja V um R-espaço vetorial n dimensional e T : V → V um operador linear. O subespaço vetorial S ≤ V
é denominado subespaço vetorial invariante pelo operador T ou subespaço vetorial T-invariante
quando T ( S ) ⊆ S , sendo T ( S ) = {T ( s ) | s ∈ S} .
Exemplo: Seja T : R 2 → R 2 tal que T ( x, y ) = (3x,8 x − y ) .
O subespaço S = {( x,2 x ), x ∈ R} é T-invariante, já que T (1,2) = (3,6) ∈ S .
Já o subespaço S ′ = {( x,0), x ∈ R} não é T-invariante, pois T (1,0) = (3,8) ∉ S ′ .
Teo90. Considere V um R-espaço vetorial n dimensional e T : V → V um operador linear. Então:
i) São subespaços T-invariantes: {0V } , V, KerT e ImT.
ii) Seja λ um autovalor do operador T. Então o autoespaço Vλ é T-invariante.
dem.: Se v ∈ T (Vλ ) então v = T (u ) , para algum u ∈ Vλ .
Se u ∈ Vλ então T (u ) = λu .
Assim, v = λu .
Então, T ( v ) = T (λu ) = λT (u ) = λ (λu ) = λv .
Logo, v ∈ Vλ .
iii) Seja S ≤ V tal que dim S = 1 . O subespaço S é T-invariante se e somente se existe um escalar
k ∈ R tal que T ( s ) = ks , para todo s ∈ S .
iv) Considere o conjunto {v, u} ⊆ V linearmente independente. [v, u ] é T-invariante se e somente se
T ( v ) ∈ [v, u ] e T (u ) ∈ [v, u ] .
 3 0 0
1 1 0
4 2 2






Exemplos: Considere os operadores: [T ] =  2 4 2  , [T ′] =  0 2 0  e [T ′′] =  1 1 0 
2 2 4
0 1 2
0 0 1






S
T(S)
T ′(S )
T ′′(S )
KerT = KerT ′ = {(0,0,0)}
Im T = Im T ′ = R 3
KerT ′′ = [(−1,1,0)]
Im T ′′ = [(1,1,0), (0,0,1)]
V2T = [(−1,1,0), (−1,0,1)]
V8T = [(1,1,1)]
{(0,0,0)}
{(0,0,0)}
{(0,0,0)}
V2T ′ = [(0,0,1)]
V3T ′ = [(1,0,0)]
V0T ′′ = [(−1,1,0)]
V1T ′′ = [(0,0,1)]
V2T ′′ = [(1,1,0)]
3
R
[(−1,1,0)]
[(1,1,0), (0,0,1)]
[(−1,1,0), (−1,0,1)]
[(1,1,1)]
[(1,1,2)]
[(2,1,1)]
[(−1,1,0)]
[(1,1,2)]
[(3,3,2)]
3
R
[(−3,2,1)]
[(3,2,0), (0,0,1)]
[(3,4,0), (0,−2,1)]
[(3,2,3)]
[(0,0,1)]
[(1,0,0)]
[(−3,2,1)]
[(0,0,1)]
[(3,2,1)]
3
R
{(0,0,0)}
Im T ′′
[(−1,−1,1)]
[(2,2,1)]
[(0,0,1)]
[(1,1,0)]
{(0,0,0)}
[(0,0,1)]
[(1,1,0)]
T-inv T ′ -inv
9
9
9
9
9
9
9
9
9
9
9
T ′′ inv
9
9
9
9
9
9
9
9
9
26
ESPAÇOS VETORIAS COM PRODUTO INTERNO E
OPERADORES LINEARES
Considere V um R-espaço vetorial n dimensional munido de um produto interno e T : V → V um
operador linear..
Operador Adjunto
Teo91. Seja f : V → R um funcional linear. Então, para todo v ∈ V existe um único vetor u ∈ V tal que
f ( v ) = v, u .
dem:
(exist.) Sejam {v1 ,..., v n } uma base ortonormal de V e u = f ( v1 )v1 + ... + f ( v n )v n ∈V
Considere v i ∈ {v1 ,..., v n } qualquer.
v i , u = v i , f ( v1 )v1 + ... + f ( v n )v n
= f (v1 ) vi , v1 + ... + f (vi ) vi , vi + ... + f (v n ) vi , v n
= f (v i )
Logo, para todo v ∈ V existe um único vetor u ∈ V tal que f (v) = v, u .
(unic.) (RAA) Supor que exista w ∈ V , w ≠ u tal que f (v) = v, w , para todo v ∈ V .
Assim, v, u = v, w
Então, v, u − w = 0
Em particular, vale a igualdade para v = u − w .
Assim, u − w, u − w = 0 sse u − w = 0V sse u = w .
Contradição.
Logo, u ∈ V é único.
Teo92. Existe um único operador linear T * : V → V tal que T ( v ), w = v, T * ( w) , para quaisquer
v , w ∈V .
dem.: Seja w ∈ V qualquer e o funcional linear f : V → R tal que f (v) = T (v), w
Pelo Teo91, existe um único vetor u ∈ V tal que f (v) = v, u
Assim, T (v), w = v, u
Considere T * : V → V tal que T * ( w) = u
Então, T (v), w = v, T * ( w)
T * é um operador linear, pois:
(po+) v ′′, T * ( v + v ′) = T ( v ′′), v + v ′ = T ( v ′′), v + T ( v ′′), v ′ = v ′′, T * ( v ) + v ′′, T * ( v ′)
27
Então, T * ( v + v ′) = T * ( v ) + T * ( v ′) , para quaisquer v, v ′ ∈V .
(po.) v ′, T * ( kv ) = T ( v ′), kv = k T ( v ′), v = k v ′, T * ( v ) = v ′, kT * ( v )
Então, T * ( kv ) = kT * ( v ) , para quaisquer k ∈ R , v ∈V .
A unicidade de T * é uma decorrência da unicidade de u.
O operador T * é denominado operador adjunto do operador T.
Exemplo: Seja T : R 2 → R 2 tal que T ( x, y ) = (3x,8 x − y ) .
O operador T * : R 2 → R 2 tal que T * ( x, y ) = (3 x + 8 y,− y ) é o operador adjunto de T.
Teo93. Seja α uma base ortonormal de V. Então [T * ]α = [T ]αt .
Teo94. Sejam T , T1 e T2 operadores lineares em V.
Então:
i)
ii)
iii)
iv)
v)
(T1 + T2 ) * = T1* + T2*
(k ⋅ T ) * = k ⋅ T * , para todo k ∈ R .
(T1 o T2 ) * = T2* o T1*
(T * ) * = T
KerT = (Im T * ) ⊥
dem.: (i) (T1 + T2 )(v), u = T1 (v) + T2 (v), u = T1 (v), u + T2 (v), u = v, T1* (u ) + v, T2* (u )
= v, T1* (u ) + T2* (u ) = v, (T1* + T2* )(u )
Teo95. Seja T : V → V um operador linear e S ≤ V um subespaço T-invariante.
Então S ⊥ é T*-invariante.
dem.: Sejam v ∈ S ⊥ e w ∈ S .
Tem-se, T * (v), w = v, T ( w) .
Como S é T-invariante, T ( w) ∈ S .
Assim, v, T ( w) = 0 .
Então, T * (v), w = 0 .
Isto é, T * (v) ∈ S ⊥ .
Logo, S ⊥ é T*-invariante.
28
Operadores Auto-Adjuntos
O operador linear T : V → V é denominado operador auto-adjunto quando T (v), u = v, T (u ) , para
quaisquer v, u ∈ V , isto é, T * = T .
Exemplos:
1) T : R 2 → R 2 tal que T ( x, y ) = (2 x + 4 y,4 x − y )
2) T : R 3 → R 3 tal que T ( x, y, z ) = ( x − y,− x + 3 y − 2 z,−2 y )
Teo96. Sejam T1 e T2 operadores lineares auto-adjuntos e k ∈ R .
Então (T1 + T2 ) e (k ⋅ T1 ) também são operadores auto-adjuntos.
dem: (T1 + T2 ) * = T1* + T2* = T1 + T2 , pelo Teo95 e por hipótese.
(k ⋅ T1 ) * = k ⋅ T * = k ⋅ T , mesmas justificativas.
Teo97. T : V → V
um operador auto-adjunto se e somente [T ]α é uma matriz simétrica, qualquer que
seja a base ortomormal α de V.
Teo98. Seja T : V → V
um operador auto-adjunto e v1 ,..., v r autovetores associados a autovalores
distintos λ1 ,..., λ r de T. Então vi é ortogonal a v j , i, j = 1,...r , i ≠ j.
dem.: Como T (vi ), v j = vi , T * (v j ) = vi , T (v j ) .
Tem-se, λi ⋅ vi , v j = vi , λ j ⋅ v j .
Assim, λi ⋅ vi , v j − vi , λ j ⋅ v j = 0
λ i v i , v j − λ j vi , v j = 0
(λ i − λ j ) v i , v j = 0
Por hipótese, λi ≠ λ j .
Logo, v i , v j = 0 .
Teo99. Seja T : V → V um operador auto-adjunto. Então T possui um autovalor real, isto é, possui um
autovetor não nulo.
Teo100. Seja T : V → V um operador auto-adjunto e v um autovetor associado ao autovalor λ de T.
Então os subespaços [v ] e [v ] ⊥ são T-invariantes.
29
Teorema Espectral para Operadores Auto-Adjuntos
Seja V um R-espaço vetorial n dimensional munido de um produto interno e T : V → V um operador
linear auto-adjunto. Então T é diagonalizável, isto é, existe uma base ortonormal α de autovetores de V
tal que [T ]α é uma matriz diagonal.
dem.: (indução em n)
Base: dim V = 1
Existe um autovetor v ∈ V , v ≠ 0V , por Teo101.
{v} é uma base de V.
 v 
  é uma base ortonormal de V.
 v 
Passo: (HI) Supor de vale o teorema para espaços vetoriais com dimensão n − 1 .
Considere v um autovetor unitário de T, vide Teo99, e dim[v] = 1 .
Mas, [v]⊥ é um subespaço T-invariante, por Teo102.
Então, T |[ v ]⊥ : [v] ⊥ → [v] ⊥ é um operador auto-adjunto.
Pela hipótese de indução, existe uma base ortonormal δ = {v1 , v 2 ,..., v n −1 } de autovetores de [v ] ⊥
tal que [T |[ v ]⊥ ]δ é uma matriz diagonal.
Mas, V = [v] ⊕ [v] ⊥ e dim V = dim[v] + dim[v] ⊥ .
Logo, {v1 , v 2 ,..., v n −1 , v} é uma base ortonormal de autovetores de V.
O espectro de um operador linear é o conjunto de seus autovalores.
30
Operadores Ortogonais
O operador linear T : V → V é denominado operador ortogonal quando T ( v ), T (u ) = v, u , isto é,
T * = T −1 .
Exemplos:
1) T : R 2 → R 2 tal que T ( x, y ) = ( y,− x)
2) T : R 3 → R 3 tal que T ( x, y, z ) = (
3
3
x+
3
3
y+
3
3
z ,−
6
3
x+
6
6
y+
6
6
z ,−
2
2
y+
2
2
z)
Teo101. Seja T : V → V um operador linear. São equivalentes:
i) T é um operador ortogonal.
ii) T transforma bases ortonormais em bases ortonormais.
iii) T preserva produto interno, isto é, T (v), T (u ) = v, u , para quaisquer v,u ∈ V .
iv) T preserva norma, isto é, T (v) = v , para todo v ∈ V .
Teo102. Seja T : V → V um operador ortogonal. Então:
i) T preserva distância.
ii) Os únicos autovalores possíveis para T são ± 1 .
iii) Autovetores de T são sempre ortogonais.
iv) Se S é um subespaço vetorial T-invariante então S ⊥ é T-invariante.
Operadores Normais
O operador linear T : V → V é denominado operador normal quando comuta com seu operador adjunto,
isto é, T o T * = T * o T .
Teo103. Seja T : V → V um operador normal. Então:
i) (k ⋅ T ) também é um operador normal.
ii) T (v) = T * (v) , para todo v ∈ V .
iii) Se λ é um autovalor de T então λ é um autovalor de T * .
iv) T e T * possuem os mesmos autovetores.
v) KerT = KerT * .
vi) Im T = Im T *
vii) ( KerT ) ⊥ = Im T .
Se V é C-espaço vetorial, o operador linear T : V → V tal que T * = T é denominado operador
hermitiano e quando T * = T −1 , operador unitário.
31
Exercícios
1) Classifique os operadores.
a) T ( x, y ) = (2 x − 2 y,−2 x + 5 y )
b) T ( x, y, z ) = ( x cosθ − y senθ , x senθ + y cosθ , z )
c) T ( x, y, z ) = (2 x + y, x + y + z , y − 3z )
 x y
2) Ache valores para x e y tais que 
 seja ortogonal.
 − 1 0
3) Dê exemplo de um operador auto-adjunto não ortogonal e vice-versa.
4) Dê exemplo de um operador normal que não é nem auto-adjunto nem ortogonal.
5) Se
e
são produtos internos sobre R2 e T : R 2 → R 2 um operador auto-adjunto em relação a
então T também é auto-adjunto em relação a
?
4
2
1


6) Seja [T ] =  4 − 5 − 4  . Verifique que T é diagonalizável sem usar os critérios de diagonalização.
2 − 4
1

7) Considere T : V → V e U : V → V operadores lineares que comutam entre si.
(C1) Se λ é um autovalor de T então Vλ é um subespaço U-invariante
(C2) Existe um autovetor comum a T e a U.
9) Todo operador auto-adjunto é um operador normal.
10) Todo operador ortogonal é um operador normal.
32
Apêndice E – Algumas demonstrações
Teo94. v) KerT = (Im T * ) ⊥
dem.: v ∈ KerT sse T (v) = 0V sse T (v), u = 0 , para todo u ∈ V sse v, T * (u ) = 0 , para todo u ∈ V sse
v ⊥ T * (u ) , para todo u ∈ V sse v ∈ (Im T * ) ⊥
Teo101. São equivalentes:
i) T é um operador ortogonal.
ii) T transforma bases ortonormais em bases ortonormais.
iii) T preserva produto interno, isto é, T (v), T (u ) = v, u , para quaisquer v,u ∈ V .
iv) T preserva norma, isto é, T (v) = v , para todo v ∈ V .
dem.:
i) → ii) α = {v1 , K, v n } base ortonormal de V
T (α ) = {T (v1 ),K, T (v n )} base de V, pois T é isomorfismo
T (vi ), T (v j ) = vi , T * (T (v j )) = vi , T −1 (T (v j )) = vi , v j = 0 , por hipótese
T (v i )
2
= T (vi ), T (vi ) = vi , T * (T (vi )) = vi , T −1 (T (vi )) = vi , vi = vi
2
= 1 , por hipótese
T (α ) base ortonormal de V
ii) → iii) α e T (α ) bases ortonormais de V
v = k1v1 + K + k n v n e u = l1v1 + K + l n v n
v, u = k1v1 + K + k n v n , l1v1 + K + l n v n =
k1l1 v1 , v1 + K + k1l n v1 , v n + K + k n l1 v n , v1 + K + k n l n v n , v n =
k1l11 + K + k1l n 0 + K + k n l1 0 + K + k n l n 1 = k1l1 + K + k n l n
T (v) = k1T (v1 ) + K + k nT (v n ) e T (u ) = l1T (v1 ) + K + l nT (v n )
T (v), T (u ) = k1T (v1 ) + K + k nT (v n ), l1T (v1 ) + K + l nT (v n ) =
k1l1 T (v1 ), T (v1 ) + K + k1l n T (v1 ), T (v n ) + K + k n l1 T (v n ), T (v1 ) + K + k n l n T (v n ), T (v n ) =
k1l11 + K + k1l n 0 + K + k n l1 0 + K + k n l n 1 = k1l1 + K + k n l n
Assim, v, u = T (v), T (u )
iii) → iv) T (v)
2
= T (v), T (v) = v, v = v
2
iv) → i) T (v) = v ∴ T (v), T (v) = v, v ∴ T * (T (v)), v = v, v ∴ T * (T (v)), v − v, v = 0 ∴
T * (T (v)) − I (v), v = 0 ∴ (T * o T − I )(v), v = 0
Mas, (T * o T − I ) * = (T * o T ) * − I * = (T * o T ) − I , isto é, (T * o T ) − I é OAA
Então, (T * o T ) − I = 0 ∴ (T * o T ) = I ∴ T * = T −1
Analogamente, (T o T * ) = I
Logo, T é OO.
Outros Teoremas:
1. T (v), u = 0 , para quaisquer v, u ∈ V sse T = 0
2.
T (v), v = 0 , para todo v ∈ V sse T * = −T
33
3. Se T é OAA e T (v), v = 0 , para todo v ∈ V então T = 0
4. Considere V um C-EVPI. T (v), v = 0 , para todo v ∈ V sse T = 0
 0 − 1
 .
Contra-exemplo para o caso real: Seja [T ] = 
 1 0
T ( x, y ), ( x, y ) = (− y, x), ( x, y ) = − xy + xy = 0
Mas, T ≠ 0
Teo102. Se T é OO então:
i) T preserva distância.
ii) Os únicos autovalores possíveis para T são ± 1 .
iii) Autovetores de T são sempre ortogonais.
iv) Se S é um subespaço vetorial T-invariante então S ⊥ é T-invariante.
dem.:
i) d (v, u ) = v − u = T (v − u ) = T (v) − T (u ) = d (T (v), T (u )) , por definição e T101iv
ii) v ∈ V , v ≠ 0V , autovetor associado ao autovalor λ
T (v), T (v) = λv, λv = λ2 v, v , por definição e prop´s PI, e T (v), T (v) = v, v , por T101iii
λ2 = 1∴ λ = ±1
iii) v, u ∈ V , v, u ≠ 0V , autovetores associados a autovalores distintos λ ≠ λ ′
T (v), T (u ) = λv, λ ′u = ± v,mu e T (v), T (u ) = v, u , por T101iii
± v , m u = v , u ∴ v, u = 0
iv) v ∈ S ⊥ e s ∈ S
T (v), T ( s ) = T (v), s ′ , pois S é T-inv e T (v), T ( s ) = v, s = 0 , por T101iii
T (v), s ′ = 0 ∴ T (v) ∈ S ⊥
Teo103. Se T é ON então:
i) (k ⋅ T ) é ON.
ii) T (v) = T * (v) , para todo v ∈ V .
iii) Se λ é um autovalor de T então λ é um autovalor de T * .
iv) T e T * possuem os mesmos autovetores.
v) KerT = KerT *
vi) Im T = Im T *
vii) ( KerT ) ⊥ = Im T .
dem.:
i) (kT ) o (kT ) * (v) = (kT ) o (kT * )(v) = (kT )[(kT * )(v)] = (kT )(kT * (v)) = kT (kT * (v)) = kk (T (T * (v)))
= kk (T * (T (v))) = kT * (kT (v)) = (kT * )(kT (v)) = (kT * )[(kT )(v)] = (kT * ) o (kT )(v)
ii) T (v)
2
= T (v), T (v) = v, T * (T (v)) = v, T (T * (v)) = T * (v), T * (v) = T * (v)
v) v ∈ KerT ∴ T (v)
2
2
2
= T (v), T (v) = 0V ,0V = 0 = T * (v) ∴ v ∈ KerT *
vii) Im T = Im T * = ( KerT ) ⊥
34