4 a parte

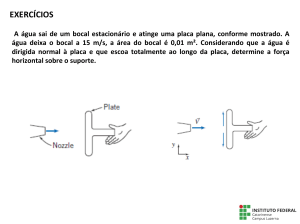
Exercício 59: (adaptado do exercício 4.60 de Fox)
O bocal mostrado na figura ao lado descarrega à
atmosfera uma lâmina d’água a 20 oC por um
arco de 180o. A velocidade da lâmina de água é
15 m/s e a espessura do jato é 30 mm, em uma
distância radial de 0.3 m, a partir da linha de
centro do tubo de suprimento, o qual tem 20 cm
de diâmetro e em que se mede uma pressão de
160 kPa. A pressão atmosférica local medida é
de 730 mmHg. Pede-se:
a-)
b-)
Determinar a vazão mássica de escoamento e a velocidade no tubo de suprimento.
Calcular as componentes z, y e x da força de sustentação do bocal, assumindo
regime permanente.
Exercício 60: (P2 – da turma 3D)
Um túnel de vento consiste basicamente de um bocal convergente, uma seção de testes
(local onde os experimentos são conduzidos), um sistema de circulação de ar e um
ventilador. A seção de testes do túnel em questão possui diâmetro de 3 m e todo o
restante do sistema de recirculação possui 6 m de diâmetro. Admita que o coeficiente de
perda de carga do bocal convergente é de 0,04 (baseado na velocidade do menor
V2
diâmetro) e todas as outras perdas podem ser estimadas como: 0, 2
(baseado na
2g
velocidade do duto de maior diâmetro).
Calcule a) a queda de pressão que o ar é submetido ao passar pelo bocal convergente e
b) a potência do motor do ventilador admitindo rendimento de 85%.
Admita ar à 20ºC, escoamento unidimensional, velocidade do escoamento na seção de
testes de 72 m/s (constante) e densidade (média) do ar de ρ ar = 1, 2 kg / m3 .
34
Exercício 60: (P2 – da turma 3D)
Quando em operação, o ventilador mostrado na figura descarrega ar com uma
velocidade de vB = 20 m/s em um fluxo de linhas de corrente com diâmetro de 0,5 m. Se
o ar tem uma densidade de 1,2 kg/m3, determine a força horizontal da reação em C.
Exercício 61:
Nos problemas estudados, considerou-se freqüentemente a hipótese de condição normal
de operação. Na prática, garantir “a condição normal” de operação nem sempre é
simples. Este exercício visa a uma reflexão sobre o uso das leis de conservação para
explicar situações reais.
1. O que é uma condição normal de operação?
2. Em muitos sítios na Mantiqueira, a “condição normal de operação” é
freqüentemente ausente (requer-se manutenção constante (quase que diária) das instalações hidráulicas, ...). O
sistema de irrigação (bastante primitivo) consiste de alguns tanques de armazenagem de
água, dos quais saem uma ou duas tubulações, às quais, podem ser subdivididas em
outras duas. Não há nenhuma bomba instalada, apenas a energia potencial é usada
como propulsora do escoamento. Reflita nas seguintes questões:
!"recomenda-se a instalação de tanques (ainda que bem pequeninos) logo após a
captação de água de poços ou de minas. Por quê?
!"o último sistema de irrigação instalado por um sitiante consiste de um tanque de
plástico de 500 (l) instalado pelo menos 4m acima dos locais a serem irrigados. Do
tanque sai uma mangueira, a qual se divide em duas. A mangueira antes de chegar
aos locais de irrigação percorre cerca de 30m, passando por arbustos, árvores e parte
de um cafezal. Completada a instalação, o sitiante abriu a válvula da saída do tanque
e foi até o local a ser irrigado e constatou que nenhuma vazão saía. O sitiante
desconfiou de um problema que poderia estar ocorrendo durante a operação
transiente do processo e conseguiu corrigir o problema. Qual poderia ter sido o
problema?
!"Um outro sistema de irrigação consiste num ponto de coleta de água através de uma
tubulação que é dividida em duas mangueiras de irrigação. O terminal de uma
mangueira de irrigação (terminal 1) situa-se a uns 150 m de distância do ponto de
35
coleta de água e o terminal 2 de irrigação a uns 110 m de distância do ponto de
coleta de água. O ponto de coleta de água situa-se a uns 9 m acima do terminal 2 e a
uns 9.3 m acima do terminal 1. A bifurcação da mangueira dá-se a uns 100 m do
ponto de coleta e situa-se a cerca de 1.5 m abaixo do terminal 2. Neste sistema de
irrigação, folhas às vezes entupiam a tubulação de coleta de água, provocando a
parada do sistema de irrigação. Tiradas as folhas, observava-se que a circulação de
água era rapidamente reestabelecida para o terminal 1, mas não chegava água para o
terminal 2. Este problema era solucionado, fechando-se a válvula da alimentação da
mangueira do terminal 1, e após reestabelecido o escoamento para o terminal 2,
abria-se a válvula para o terminal 1 e o funcionamento do sistema de irrigação
voltava à sua aparente normalidade.
Exercício 62:
Durante a fase de pré-projeto de um espargidor (soprador de folhas), deseja-se
determinar os esforços aos quais o operador do equipamento será submetido. Um
esquema do dispositivo é mostrado em duas vistas na figura (são omitidos alguns
detalhes construtivos). O ar entra por um duto lateral (designado na figura por duto de
entrada de ar, seção 1), passa por um ventilador e é direcionado por um duto de plástico
estirado de 10 cm de diâmetro interno e 120 cm de comprimento (seção 2) até um bocal
de saída (seção 3). Em uma aproximação, admita que a pressão do jato (seção 3) seja a
pressão atmosférica. Suponha também, que apenas a perda de carga no duto de plástico
estirado seja significativa (em outras palavras, despreze todas as outras perdas por atrito,
inclusive a perda no bocal de saída).
Hipóteses adicionais:
1. Para o ponto (1) fora do espargidor a pressão é atmosférica e a velocidade é próxima
de zero.
2. Despreze variações na energia potencial (dica: na equação da conservação da
energia é possível desprezar as diferenças de altura entre as seções).
3. Admita o escoamento do ar como sendo incompressível.
4. Despreze o peso do ar no interior do espargidor.
São dados:
Velocidade do jato de ar na saída do espargidor (seção 3):
240 (km /h)
Área do jato de saída do espargidor (seção 3):
30 (cm2 )
Massa do conjunto (ventilador, duto, bocal e demais acessórios sólidos): 10 (kg)
Viscosidade dinâmica ou absoluta do ar:
1.81×10-5(Pa.s)
36
Pede-se:
a)
b)
c)
d)
e)
A densidade do ar atmosférico a 20oC.
A vazão mássica de ar através do espargidor e a velocidade de escoamento
na seção 2 (considere o espargidor trabalhando em regime permanente).
A perda de carga no duto de plástico estirado.
A potência do ventilador supondo um rendimento de 65%.
Os esforços que o operador terá que realizar, a saber: a força horizontal
(paralela ao eixo x) e a força vertical (paralela ao eixo y). Dica: efetue para
tanto um balanço de quantidade de movimento entre os pontos 1 e 3.
Exercício 63:
Água à 60oC escoa através de um convergente conforme mostrado na figura. São dados:
Propriedades da água a 60oC: densidade 983 kg/m3 e viscosidade 0,467 x 10 -3 Pa.s
Propriedades do mercúrio à 60oC: densidade 13000 kg/m3.
Seção 1: Diâmetro de 7 cm, pressão manométrica de 101325 Pa
Seção 2: Diâmetro de 4 cm
Vazão volumétrica de 0,010 m3/s.
Admita desprezíveis todos os tipos de perdas por atrito e também a dimensão a muito
menor que a dimensão h.
37
Determine:
a) A pressão na seção 2 e a força necessária
para conter as flanges do convergente.
b) O desnível do manômetro diferencial de
mercúrio.
c) Haverá cavitação (sim ou não e em qual
seção)? Justifique.
Exercício 64:
Considere a instalação hidráulica de diâmetro interno constante igual a 2.5 cm
desenhada a seguir, em que a válvula é flangeada e o cotovelo rosqueado à tubulação.
Sabe-se que pela instalação hidráulica escoa um fluido com velocidade média de 2 m/s e
que o fator de atrito de Darcy-Weissbach é de 0.02. Sabendo-se que entre os pontos 1 e
2 a perda de carga distribuída é de 2m, pede-se:
a-)
calcular a perda de carga total entre os pontos 1 e 2.
b-)
qual o comprimento equivalente associado à perda de carga na válvula?
Exercício 65:
Um medidor de velocidade está fixo e obtém o seguinte sinal para um determinado
escoamento:
Assinale V para verdadeiro e F para Falso (Justificar):
( ) Durante o intervalo tA e tC o escoamento encontra-se em regime transitório
( ) As flutuações de velocidade indicam que o escoamento em tB e tC é turbulento
( ) A viscosidade impede que ocorram oscilações de velocidade durante tA
38
( ) Se o escoamento estivesse ocorrendo dentro de um misturador de fluidos, a
eficiência do processo de mistura seria maior durante o tempo tC
( ) O escoamento se desenvolve como se o fluido tivesse viscosidade nula
( ) Não é possível, apenas avaliando o gráfico, determinar se o fluido é newtoniano ou
não newtoniano
Exercício 66:
Ar escoa através de um bocal convergente / divergente, conforme a figura. A seção de
menor área é conhecida como garganta. Para o problema ilustrado a densidade do ar na
garganta é de ρG = 1, 2 kg / m3 e a vazão em massa que atravessa essa seção é de
m! G = 11, 64 kg / s . Suponha escoamento unidimensional e temperatura na garganta de
T=20 ºC. Determine se o escoamento é compressível ou incompressível (justifique).
Dica: velocidade do som c = λ RT , onde λ é a razão entre os calores específicos, que
para o ar pode ser admitido como λ = 1, 4 .
Exercício 67:
A figura abaixo ilustra o escoamento em um canal retangular, de largura 4m
(perpendicular ao plano do papel). Qual é a velocidade média e a vazão em volume que
atravessa o canal?
Exercício 68:
O bocal plano da figura abaixo de seção retangular W × b descarrega verticalmente para
baixo na atmosfera, sendo que logo ao sair do bocal o jato tem velocidade de 12.2 (m/s)
e seção transversal w × b (seção 2 no desenho). O bocal é alimentado com um fluxo
permanente de água a 20 (oC) a uma vazão volumétrica de 0.0155 (m3/s) e as
dimensões W e w são respectivamente 51.8 (mm) e 12.7 (mm). Uma placa plana,
inclinada, colocada 4.85 (m) abaixo do bocal, é atingida pela corrente d’água. Efeitos
de atrito são desprezíveis no bocal e no trajeto aberto à atmosfera. Admita, também,
que não há interrupções no jato de água durante seu trajeto de queda.
39
Pede-se:
a-) Determinar a largura normal ao plano do papel (b) e a velocidade na seção W × b.
b-) Calcular a velocidade da água imediatamente antes do contato com a placa
inclinada (V3). Sabe-se que devido à ação da gravidade, a velocidade da água
durante a queda aumenta, e por esse motivo, a espessura (w) do jato descendente
diminui.
c-) Determinar a magnitude das componentes na direção x e y esquematizadas na
figura da força necessária para manter a placa parada, admitindo que a corrente
d’água se divide igualmente em duas correntes com velocidades iguais a V.
Nos cálculos despreze o peso próprio da placa assim como o peso próprio da
água sobre ela.
Exercício 69:
Um experimento para visualização do fenômeno da cavitação é montado no laboratório
de Fenômenos de Transporte. Um tubo de venturi (convergente / divergente) de vidro é
instalado em uma seção da bancada de testes. Admitindo que todos os tubos tenham o
mesmo diâmetro e que a perda de carga no venturi é muito pequena (desprezível) assim
como a perda de carga na tubulação de sucção da bomba e nas saídas das tubulações.
Utilizando no experimento água à 20ºC, determine:
a) Qual o regime do escoamento na tubulação do circuito onde o venturi está
instalado?
b) Qual o fator de atrito na tubulação?
c) Qual a perda de carga total entre as seções (0) e (5)?
d) Qual a potência da bomba da instalação supondo rendimento de 80% ?
Há uma tubulação de retorno (tanque II para tanque I) para manutenção do regime
permanente durante a realização do experimento (níveis constantes dos tanques). Para
que isso ocorra, é necessário que a válvula borboleta instalada na tubulação de retorno
tenha uma determinada abertura, de modo que a vazão na tubulação da seção de testes
seja exatamente igual à vazão na tubulação de retorno. Sabendo que a perda de carga da
válvula varia conforme o ângulo de abertura da válvula, determine:
e) Qual deve ser o coeficiente de perda de carga localizada da válvula borboleta
para garantir o regime permanente?
f) A que ângulo de abertura (APROXIMADO) esse coeficiente de perda de carga
corresponde? Dica: O gráfico abaixo exprime a variação do coeficiente de perda
de carga em função do ângulo de abertura para a válvula borboleta.
40
g) Um vacuômetro instalado na seção da garganta (G) do venturi registra a pressão
de pG = −20000 Pa (manométrica, portanto na escala efetiva). Sabendo que a
pressão atmosférica local é de 100000 Pa, haverá cavitação? Justifique sua
resposta.
h) Se, durante o ensaio, alguém fecha completamente a válvula da tubulação de
retorno, sabendo que o tanque II é cúbico e possui altura total de 1,2 m, em
quanto tempo (a partir deste instante) haverá transbordamento?
São dados: Área da seção transversal do duto, A = 0,002 m2; Vazão em volume da
água, Q = 6 litros / s ;
Tubos de ferro fundido com rugosidade, ε = 0, 26 mm ;
Coeficiente de perda de carga localizada para cotovelo, k = 0,39; Coeficiente de perda
de carga singular para entrada (em tubulação) com cantos vivos, k = 0,5;
Exercício 70: (adaptado do exercício P3.12 de White)
Um tanque fechado, com três tubulações anexadas, encontra-se totalmente preenchido
com água a 20oC. Pela tubulação 1 de diâmetro igual a 6cm entra água a 20oC com uma
vazão volumétrica de 100m3/h. Pela tubulação 2 de 5cm de diâmetro sai água a 20oC
com uma velocidade média de 8m/s. Se o diâmetro da 3a tubulação for de 4cm qual será
a velocidade média na seção 3? Água saíra ou entrará por esta tubulação? Resposta:
9.6(SI)
41