Aula: 13 Temática: Transformações Físicas das Substâncias Puras

Aula: 13
Temática: Transformações Físicas das Substâncias Puras
Uma das formas mais compactas de apresentação das mudanças de
estado físico de uma substância é a do diagrama de fase. Vamos estudá-lo.
Fase de uma substância é a forma homogênea da matéria quanto à
composição química e ao estado físico, são classificadas como sólida, líquida e
gasosa. Uma transição de fase é a conversão espontânea de uma fase em
outra, ocorrendo à pressão e temperatura características. A 1 atm, o gelo é a
fase estável da água quando abaixo de 0°C, mas acima de 0°C é a fase líquida
a mais estável. Tal diferença mostra que abaixo de 0°C, o potencial químico do
gelo é mais baixo que o da água líquida e o inverso acontece para
temperaturas acima de 0°C. Na temperatura de transição, Ttrs, os potenciais
químicos são iguais, as duas fases estão em equilíbrio e a pressão constante.
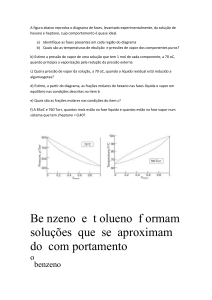
A Figura 2.2 mostra a dependência entre o potencial químico das fases de uma
substância pura e a temperatura, onde Tf é a temperatura de fusão e Teb é a
temperatura de ebulição e constituem as temperaturas de transição.
Figura 2. 1. Dependência do potencial químico de uma substância pura com a temperatura.
As
regiões
de
pressão
e
de
temperatura
em
que
as
fases
são
termodinamicamente estáveis podem ser observadas em um diagrama de
fase. As curvas de equilíbrio separam as regiões dando os valores de p e T
nos quais as duas fases coexistem em equilíbrio. Nesse diagrama, a fronteira
entre as fases líquida e o vapor mostra como a pressão de vapor (as duas
fases em equilíbrio) varia com a temperatura. Do mesmo modo, a fronteira
entre as fases sólidas e o vapor mostra a variação da pressão de vapor na
FÍSICO-QUÍMICA
sublimação com a temperatura. A pressão de vapor de uma substância
aumenta com a temperatura.
O aquecimento de um líquido em um recipiente aberto causa uma vaporização
na superfície. A vaporização ocorre no centro da massa do líquido quando a
pressão de vapor é igual à pressão externa, sendo que esta condição de
vaporização livre, em toda a massa do líquido, é a ebulição. Para a pressão
externa de 1 atm, a temperatura de ebulição correspondente é o ponto de
ebulição normal, Teb. O uso da pressão padrão sugere a utilização do ponto
de ebulição padrão, como a temperatura em que a pressão de vapor é de 1
bar. Sendo 1 bar = 0,987 atm, o ponto de ebulição padrão é um pouco mais
baixo que o normal.
No caso de aquecimento de um líquido em recipiente fechado, a ebulição não
ocorre. A pressão de vapor, e, portanto a densidade do vapor, eleva-se
continuamente à medida que a temperatura aumenta. Por outro lado, a
densidade do líquido diminui devido a sua expansão. No ponto em que as
densidades se igualam, do vapor e do líquido remanescente, a superfície entre
as duas fases desaparece. A temperatura neste momento é a temperatura
crítica, Tc, da substância. A pressão de vapor na temperatura crítica é a
pressão de vapor, pc. Na temperatura crítica e acima dela existe uma única
fase uniforme, o fluido supercrítico, não havendo nenhuma interface e não
existindo mais a fase líquida.
Vejamos a Figura 2.3 que mostra a representação em gráfico do que foi dito.
Figura 2. 2. Diagrama de fases com as regiões de T e p onde cada fase é estável
FÍSICO-QUÍMICA
Existe um par, pressão-temperatura, em que as três fases da substância
coexistem em equilíbrio. Representa o ponto triplo, um ponto em que as três
curvas de equilíbrio se encontram. A temperatura neste ponto é indicada como
T3 ou Tt.
A temperatura de fusão indica que as fases sólida e líquida de uma
substância coexistem, sob certa pressão. As temperaturas de fusão e
congelamento são idênticas. O ponto de fusão normal, Tf, é a temperatura de
fusão a 1 atm e o ponto de fusão padrão é a temperatura para pressão de 1
bar, mas para a maior parte das aplicações a diferença é desprezível.
O critério termodinâmico para o equilíbrio é um resultado da segunda lei da
termodinâmica: no equilíbrio, o potencial químico de uma substância é
constante numa amostra, qualquer que seja o número de fases presentes.
Se em um sistema existirem dois pontos com potenciais químicos diferentes de
uma substância, µ1 e µ2, é deslocado um certo número de mols de um ponto
para outro (dn). A energia de Gibbs diminui (−µ1dn) no ponto de onde foi
deslocado e a aumenta (+µ2dn) no ponto aonde chegam os mols. A variação é
dG = (µ2 − µ1)dn, sendo o potencial químico em 1 maior que em 2, a
transferência de mols é acompanhada por uma diminuição de G, ocorrendo
espontaneamente. Somente se µ1 = µ2 não haverá mudança de G e o sistema
estará em equilíbrio.
O potencial químico de uma substância pura é a energia de Gibbs molar e
como a dependência entre G e a temperatura é expressa em termos da
entropia do sistema, temos:
 ∂µ 
  = −Sm .
 ∂T  p
Pela equação vemos que o aumento da temperatura determina uma diminuição
do potencial químico de uma substância pura. Lembremos que Sm é sempre
positivo.
FÍSICO-QUÍMICA
A maior parte das substâncias puras funde a uma temperatura maior que a
atmosférica, como se o aumento da pressão impedisse a formação da fase
líquida menos densa (volume maior). A água é uma exceção, já que o líquido é
mais denso que o sólido, logo a aplicação da pressão à água favorece a
formação da fase líquida e o congelamento acontece à temperatura mais baixa.
Vejamos a equação:
 ∂µ 
  = Vm
 ∂p T
A equação mostra que o coeficiente angular da curva do potencial químico pela
pressão é igual ao volume molar da substância. Assim, a elevação de p eleva o
potencial químico de qualquer substância pura, pois Vm > 0. Em geral, o efeito
do aumento da pressão é o de elevar ligeiramente a temperatura de fusão,
entretanto, com a água, o ponto de fusão sofre ligeiro abaixamento.
Exercícios Propostos
1. A entalpia padrão de combustão do fenol sólido (C6H5OH) é –3054 kJ / mol
a 298 K e a sua entropia molar padrão é 144,0 J / K mol. Calcular a energia de
Gibbs padrão de formação do fenol a 298 K.
2. Calcular o trabalho máximo, diferente do de expansão, que pode ser
obtido, por mol, numa pilha a combustível em que se queima metano a 298 K.
3. A 25ºC calcule o valor de A para uma expansão isotérmica de um mol de
um gás ideal que varia de 10 litros para 40 litros.
Analisamos as transformações físicas das substâncias puras através
do estudo do diagrama de fases. Também verificamos a estabilidade das fases
e o critério termodinâmico para o equilíbrio.
FÍSICO-QUÍMICA